Океанология, 2022, T. 62, № 2, стр. 301-308

К определению глубины замыкания у песчаного берега

И. О. Леонтьев^*

Институт океанологии им. П.П. Ширшова РАН
Москва, Россия

Поступила в редакцию 04.02.2021
После доработки 25.02.2021
Принята к публикации 08.04.2021

EDN: EKFWVV
DOI: 10.31857/S0030157422020101

Аннотация

Глубина замыкания ${{h}_{*}}$ ограничивает область существенных морфологических изменений профиля дна в масштабе года, и ее прогноз важен для практических приложений. Обсуждаются возможные причины плохого соответствия предложенных ранее аналитических оценок ${{h}_{*}}$ с данными наблюдений. Предпринята попытка определить ${{h}_{*}}$ на основе принципа сохранения массы, трактующего деформации дна как следствие градиентов транспорта наносов. Принимаются во внимание два главных механизма поперечного транспорта наносов в береговой зоне – асимметрия волновых скоростей и противотечение. Получена формула, согласно которой глубина ${{h}_{*}}$ пропорциональна высоте волн ${{H}_{{s012}}}$, превышение которой возможно не более 12 ч в году. Фактор пропорциональности зависит от крутизны волн и порога деформаций дна $\Delta {{h}_{с}}$, связанного с точностью промеров глубин. Для типичных значений $\Delta {{h}_{с}}$ от 0.1 до 0.3 м глубина ${{h}_{*}}$ изменяется от $(1.5~{\kern 1pt} - {\kern 1pt} 1.6){{H}_{{s012}}}$ до $(1.1~{\kern 1pt} - {\kern 1pt} 1.2){{H}_{{s012}}}$. Сравнение с данными наблюдений показывает, что предсказанное значение ${{h}_{*}}$ является репрезентативным показателем глубины замыкания на песчаных берегах с небольшой высотой прилива.

Ключевые слова: глубина замыкания, береговой профиль, деформации дна, транспорт наносов, принцип сохранения массы

ВВЕДЕНИЕ

Глубина замыкания ${{h}_{*}}$ (depth of closure) маркирует границу активной части берегового профиля, в пределах которой возможны значимые штормовые деформации дна в масштабе года. Подвижки наносов отмечаются и на глубинах, превосходящих ${{h}_{*}}$, но связанные с ними изменения не превышают установленный порог. Морфодинамическая граница, характеризуемая глубиной ${{h}_{*}}$, важна как для модельных исследований [2], так и для проектов, направленных на укрепление и защиту берегов [3, 11], что вызывает значительный интерес к оценке ${{h}_{*}}$.

Стандартный метод определения ${{h}_{*}}$ в полевых условиях основывается на повторных промерах профилей и анализе отклонений глубин $\Delta h$ в одних и тех же точках [9, 15]. Как показывают наблюдения, с удалением от берега значения $\Delta h$ уменьшаются и за пределами зоны подводных валов достигают некоторого минимального порога $\Delta {{h}_{с}}$, определяемого точностью измерений (в типичном случае порядка 0.1 м), что служит индикатором местоположения глубины замыкания на профиле (рис. 1). Выбор порога $\Delta {{h}_{с}}$, очевидно, влияет на величину глубины ${{h}_{*}}$, что не всегда учитывается при сопоставлении результатов различных исследований.

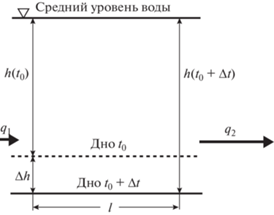
Рис. 1.

Годовые изменения глубины $h$ и распределение деформаций дна $\Delta h$ на береговом профиле. Глубина замыкания ${{h}_{*}}$ отвечает заданному минимальному порогу деформаций $\Delta {{h}_{с}}$.

Предложен также альтернативный способ оценки ${{h}_{*}}$, основанный на анализе распределения среднего размера песка ${{d}_{g}}$ на подводном склоне [4]. Авторы исследования обнаружили наличие устойчивого минимума ${{d}_{g}}$ в определенной точке профиля, положение которого практически совпадает с глубиной замыкания, определяемой стандартным способом.

Что касается аналитических оценок ${{h}_{*}}$, то наиболее известный результат получен Халлермейером [12], который установил зависимость ${{h}_{*}}$ от высоты волн наиболее сильных штормов с суммарной продолжительностью 12 ч в году. Речь идет о значительной высоте волн на глубокой воде ${{H}_{{s012}}}$ с обеспеченностью (вероятностью превышения) 0.137%. Данный выбор аргументируется тем, что в ходе 12-часового волнового воздействия профиль дна более или менее стабилизируется, приближаясь к равновесному состоянию.

При определении ${{h}_{*}}$ Халлермейер исходил из эмпирического критерия “интенсивного возмущения дна (intense bed agitation)”, выраженного в форме числа Фруда и подразумевающего условия развитого транспорта песчаных наносов (sheet flow). Однако перемещение песка само по себе не означает изменений морфологии дна. Деформации дна возникают вследствие изменений транспорта наносов по длине профиля. Поэтому для определения границы значимых донных деформаций (т.е. глубины ${{h}_{*}}$) более целесообразным представляется подход, принимающий во внимание связь изменений дна с градиентами транспорта наносов.

Одним из стимулов данного исследования послужило то обстоятельство, что теоретические оценки ${{h}_{*}}$ плохо согласуются с результатами наблюдений. В настоящей работе предпринимается попытка оценить глубину замыкания, исходя из принципа сохранения массы, позволяющего представить морфологические изменения как следствие изменений расхода наносов по протяжению профиля берега.

СУЩЕСТВУЮЩИЕ ЗАВИСИМОСТИ

Аналитическая зависимость для расчета ${{h}_{*}}$, полученная в упомянутой работе [12], выглядит как

(1)

${{h}_{*}} = 2.28{{H}_{{s012}}} - 68.5\left( {\frac{{H_{{s012}}^{2}}}{{g{{T}^{2}}}}} \right),$

где $T$ – период волн, соответствующий высоте ${{H}_{{s012}}}$, $g$ – ускорение силы тяжести. Приняв во внимание соотношение между периодом и длиной волн на глубокой воде ${{L}_{0}} = \frac{{g{{T}^{2}}}}{{2\pi }}$, формулу (1) можно представить в виде

(2)

${{h}_{*}} = {{K}_{0}}{{H}_{{s012}}},\,\,\,\,{{K}_{0}} = 2.28 - 10.9\left( {\frac{{{{H}_{0}}}}{{{{L}_{0}}}}} \right).$

Очевидно, с ростом крутизны волн ${{{{H}_{0}}} \mathord{\left/ {\vphantom {{{{H}_{0}}} {{{L}_{0}}}}} \right. \kern-0em} {{{L}_{0}}}}$ глубина замыкания должна уменьшаться. При типичной крутизне штормовых волн 0.04 из зависимости (2) следует ${{h}_{*}} = 1.84{{H}_{{s012}}}$. Недостатком формулы Халлермейера является отсутствие ее привязки к конкретному порогу деформаций дна $\Delta {{h}_{с}}$, что затрудняет ее сопоставление с данными натурных исследований.

Исследования изменчивости батиметрии береговых профилей в морских условиях [6, 14, 15] показали, что глубина ${{h}_{*}}$ оказывается заметно меньше, чем следует из формулы (1) и, как правило, не превышает значений $(1.5~{\kern 1pt} - {\kern 1pt} 1.6){{H}_{{s012}}}$. Это перекликается с результатом [13] в отношении глубины ${{h}_{l}}$, ограничивающей вдольбереговой транспорт наносов, которая связана с высотой обрушающихся волн ${{H}_{{sB}}}$ соотношением ${{h}_{l}} = 1.6{{H}_{{sB}}}$.

В работе [9], основанной на данных промеров в районе Дак (Северная Каролина, США), предложена эмпирическая формула вида

(3)

${{h}_{*}} = {{a}_{*}}H_{{s012}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}},$

где коэффициент ${{a}_{*}}$ зависит от заданного порога деформаций дна $\Delta {{h}_{с}}$. Для его значений 0.05, 0.1 и 0.2 м величина ${{a}_{*}}$ составляет 3.4, 2.8 и 2.1 соответственно, т.е. с ростом $\Delta {{h}_{с}}$ глубина замыкания уменьшается. Формула (3) ограничивается сравнительно небольшими высотами волн ${{H}_{{s012}}}$ до 3–4 м.

Все приведенные оценки ${{h}_{*}}$ относятся к временному масштабу порядка 1 года. При увеличении рассматриваемого периода времени значения ${{h}_{*}}$ будут возрастать, поскольку в расчет будут приниматься все более редкие штормовые события, оставляющие свой след на большей глубине. Так, для интервала 50–100 лет глубина замыкания, по мнению Брууна [8], может определяться величиной ${{h}_{*}} = 3.5{{H}_{{Bm}}}$, где ${{H}_{{Bm}}}$ – максимальная высота волн в точке обрушения за данный период.

ОЦЕНКА ГЛУБИНЫ ЗАМЫКАНИЯ НА БАЗЕ ПРИНЦИПА СОХРАНЕНИЯ МАССЫ

Рассмотрим баланс наносов на выделенном участке песчаного дна длиной $l$ (рис. 2). Объемные расходы наносов на входе и выходе равны соответственно ${{q}_{1}}$ и ${{q}_{2}}$. Вследствие изменения расхода в пределах участка дно должно деформироваться, и за период времени $\Delta t$ изменение глубины $h$ составит $\Delta h$. Условие сохранения объема или массы осадков при отсутствии дополнительных источников и стоков, очевидно, выразится равенством

(4)

$\left( {{{q}_{2}} - {{q}_{1}}} \right)\Delta t = l\Delta h.$

Характеризуя масштаб изменений дна, допустим, что на расстоянии $l$ расход наносов изменяется вдвое (${{q}_{1}} = \frac{1}{2}q$, ${{q}_{2}} = q$), а само расстояние измеряется половиной длины волн $L$, т.е. $l = \frac{1}{2}~L$. Тогда соотношение (4) принимает вид

(5)

$\frac{q}{L} = \frac{{\Delta h}}{{\Delta t}}.$

Расход наносов $q$ является функцией глубины, параметров волн и свойств наносов. Поэтому, определив $q$, можно найти из соотношения (5) глубину $h$, на которой при данном волнении в течение времени $\Delta t$ будет достигнута заданная величина деформаций дна $\Delta h$.

Рис. 2.

Деформации дна при изменении расхода наносов. Обозначения в тексте.

При параметризации величины $q$ будем опираться на известную формулу расхода влекомых наносов, следующую из энергетической концепции [5, 7]:

(6)

$\begin{gathered} q = \mu \frac{1}{2}{{f}_{w}}\rho \frac{{{{\varepsilon }_{b}}}}{{{\text{tg}}{{\alpha }_{g}}}}\overline {u{{{\left| u \right|}}^{2}}} , \\ \mu = {{\left[ {g\left( {{{\rho }_{g}} - \rho } \right)\left( {1 - \sigma } \right)} \right]}^{{ - 1}}}, \\ \end{gathered} $

где $\mu $ – коэффициент перехода от погруженного веса песка к его объему (м³м^–1с^–1), $g$ – ускорение силы тяжести, ${{\rho }_{g}}$ и $\rho $ – плотности частиц песка и воды, σ – пористость грунта, ${{f}_{w}}$ – коэффициент донного трения, ${{\varepsilon }_{b}}$ – коэффициент эффективности транспорта (0.1), ${{\alpha }_{g}}$ – угол естественного откоса (${\text{tg}}{{\alpha }_{g}} \cong $ 0.6), $u$ – скорость течения у дна, горизонтальная черта означает осреднение за период волн. При стандартных значениях плотности воды и песка (1.0 × 10³ и 2.6 × 10³ кг м^–3), а также его пористости (0.4) имеем соотношение $\mu \rho \cong \frac{1}{g}$, используемое в дальнейшем.

К числу основных механизмов, контролирующих транспорт наносов на береговом профиле, относятся асимметрия волновых скоростей и противотечение (undertow), компенсирующее стоксов перенос воды к берегу. Далее отдельно рассмотрим вклады каждого из механизмов.

Асимметрия волн

Предполагается, что величина $u$ в формуле (6) включает вклады гармоник орбитальной волновой скорости с амплитудами ${{u}_{m}}$ и ${{u}_{{2m}}}$ и сдвигом фаз ${{\Phi }}$,

(7)

$\begin{gathered} u = {{u}_{m}}\cos \omega t + {{u}_{{2m}}}\cos \left( {2\omega t + {{\Phi }}} \right), \\ {{u}_{{2m}}} \ll {{u}_{m}}, \\ \end{gathered} $

где $\omega = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } T}} \right. \kern-0em} T}$ – частота колебаний, $T$ – их период, $t$ – время. Тогда третий нечетный момент скорости в (6) определится как $\overline {u{{{\left| u \right|}}^{2}}} = \frac{3}{4}u_{m}^{3}\frac{{{{u}_{{2m}}}}}{{{{u}_{m}}}}\cos \Phi $ [7].

По мере трансформации волн отношение амплитуд гармоник увеличивается пропорционально параметру Урселла $Ur$, но одновременно уменьшается $\cos \Phi $ за счет сдвига фаз гармоник [17]. Приведенные выше оценки ${{h}_{*}}$ свидетельствуют о том, что ${{{{H}_{{s012}}}} \mathord{\left/ {\vphantom {{{{H}_{{s012}}}} {{{h}_{*}}}}} \right. \kern-0em} {{{h}_{*}}}} \approx 0.5{\kern 1pt} - {\kern 1pt} 0.7$. Это означает, что глубина ${{h}_{*}}$ располагается достаточно близко к точке обрушения волн с высотой ${{H}_{{s012}}}$, где $\Phi \to \frac{\pi }{2}$ и $\cos \Phi \to 0$. Можно допустить в первом приближении, что в районе глубины замыкания $\cos \Phi \approx {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$, и тогда

(8)

$\frac{{{{u}_{{2m}}}}}{{{{u}_{m}}}}\cos \Phi \approx \frac{1}{2}Ur = \frac{1}{2}\frac{3}{8}\frac{{kH}}{{{{{\left( {kh} \right)}}^{3}}}},$

где $H$ – высота волн, $k = \frac{{2{{\pi }}}}{L}$ – волновое число, $L$ – длина волн. В результате, используя мелководные аппроксимации линейной теории волн $L = T\sqrt {gh} $ и ${{u}_{m}} = \frac{1}{2}\frac{H}{h}\sqrt {gh} $, получим соотношение $~\overline {u{{{\left| u \right|}}^{2}}} = \frac{{9{{g}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}{{512}}\frac{{{{L}_{0}}}}{{2{{\pi }}}}\frac{{{{H}^{4}}}}{{{{h}^{{{7 \mathord{\left/ {\vphantom {7 2}} \right. \kern-0em} 2}}}}}}$, где ${{L}_{0}} = \frac{{g{{T}^{2}}}}{{2\pi }}$ – длина волн на глубокой воде.

Коэффициент трения ${{f}_{w}}$ определим на основе зависимости [16]:

(9)

${{f}_{w}} \approx 0.2{{\left( {\frac{{{{a}_{m}}}}{r}} \right)}^{{ - 0.5}}},$

где ${{a}_{m}} = \frac{{{{u}_{m}}}}{\omega }$ – амплитуда колебаний частиц воды вдоль дна, $r$ – параметр донной шероховатости.

С учетом всех приведенных соотношений получим

(10)

$\begin{gathered} \frac{q}{L} = {{c}_{1}}\frac{{{{{\left( {gr} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{{{{\left( {{H \mathord{\left/ {\vphantom {H {{{L}_{0}}}}} \right. \kern-0em} {{{L}_{0}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}}}\frac{{{{H}^{{{{15} \mathord{\left/ {\vphantom {{15} 4}} \right. \kern-0em} 4}}}}}}{{{{h}^{{{{15} \mathord{\left/ {\vphantom {{15} 4}} \right. \kern-0em} 4}}}}}}, \\ {{c}_{1}} = \frac{{0.2{{{\left( 2 \right)}}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}}}{{4{{\pi }^{{{5 \mathord{\left/ {\vphantom {5 4}} \right. \kern-0em} 4}}}}}}\frac{9}{{512}}\frac{{{{\varepsilon }_{b}}}}{{{\text{tg}}{{\alpha }_{g}}}}. \\ \end{gathered} $

Подставив (10) в (5), придем к следующему соотношению между локальной высотой волн и глубиной:

(11)

$h = {{\left( {{{c}_{1}}\frac{{\Delta t}}{{\Delta h}}} \right)}^{{{4 \mathord{\left/ {\vphantom {4 {15}}} \right. \kern-0em} {15}}}}}\frac{{{{{\left( {gr} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 {15}}} \right. \kern-0em} {15}}}}}}}{{{{{\left( {{H \mathord{\left/ {\vphantom {H {{{L}_{0}}}}} \right. \kern-0em} {{{L}_{0}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 {15}}} \right. \kern-0em} {15}}}}}}}H.$

Чтобы выразить локальную высоту волн $H$ в терминах глубокой воды ${{H}_{0}}$, используем условие постоянства потока энергии. При распространении волн по нормали к берегу имеем ${{H}^{2}}{{C}_{g}} = H_{0}^{2}{{C}_{{g0}}}$, где ${{C}_{g}} = \sqrt {gh} $ и ${{C}_{{g0}}} = \frac{1}{2}\frac{{gT}}{{2\pi }}$ – групповые скорости волн на мелкой и глубокой воде соответственно. Выполнив ряд преобразований, можно прийти к зависимости

(12)

$H = \frac{{{{\gamma }^{{{1 \mathord{\left/ {\vphantom {1 5}} \right. \kern-0em} 5}}}}}}{{{{2}^{{{2 \mathord{\left/ {\vphantom {2 5}} \right. \kern-0em} 5}}}}{{{\left( {2\pi } \right)}}^{{{1 \mathord{\left/ {\vphantom {1 5}} \right. \kern-0em} 5}}}}}}{{\left( {\frac{{{{H}_{0}}}}{{{{L}_{0}}}}} \right)}^{{ - {1 \mathord{\left/ {\vphantom {1 5}} \right. \kern-0em} 5}}}}{{H}_{0}},\,\,\,\,\gamma = {H \mathord{\left/ {\vphantom {H h}} \right. \kern-0em} h}.$

Как уже отмечалось, в районе глубины замыкания величина $\gamma $ должна быть близка к 0.5–0.7, что приводит к соотношению $H \cong \frac{{0.47}}{{{{{\left( {{{{{H}_{0}}} \mathord{\left/ {\vphantom {{{{H}_{0}}} {{{L}_{0}}}}} \right. \kern-0em} {{{L}_{0}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 5}} \right. \kern-0em} 5}}}}}}{{H}_{0}}$. Подставив его в (11), используем аппроксимацию ${{\left( {{H \mathord{\left/ {\vphantom {H {{{L}_{0}}}}} \right. \kern-0em} {{{L}_{0}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 {15}}} \right. \kern-0em} {15}}}}} \approx {{\left( {{{{{H}_{0}}} \mathord{\left/ {\vphantom {{{{H}_{0}}} {{{L}_{0}}}}} \right. \kern-0em} {{{L}_{0}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 {15}}} \right. \kern-0em} {15}}}}}$. Далее примем продолжительность волнового воздействия $\Delta t$ = 12 ч (12 × × 3600 c) и в результате получим формулу глубины замыкания:

(13)

${{h}_{*}} = {{K}_{1}}{{H}_{{s012}}},\,\,\,\,{{K}_{1}} = 0.74\frac{{{{r}^{{{2 \mathord{\left/ {\vphantom {2 {15}}} \right. \kern-0em} {15}}}}}}}{{\Delta {{h}^{{{4 \mathord{\left/ {\vphantom {4 {15}}} \right. \kern-0em} {15}}}}}}}{{\left( {\frac{{{{H}_{0}}}}{{{{L}_{0}}}}} \right)}^{{ - {4 \mathord{\left/ {\vphantom {4 {15}}} \right. \kern-0em} {15}}}}},$

где $\Delta h$ соответствует выбранному порогу деформаций дна $\Delta {{h}_{с}}$.

Противотечение

Полагаем, что скорость $u$ в формуле расхода (6) включает вклады волновой составляющей и среднего течения $\bar {u}$,

(14)

$u = {{u}_{m}}\cos \omega t + \bar {u},\,\,\,\,\bar {u} \ll {{u}_{m}}.$

В этом случае момент скорости в (6) выразится как $\overline {u{{{\left| u \right|}}^{2}}} = \frac{3}{2}u_{m}^{2}\bar {u}$, где скорость противотечения $\bar {u}$ в мелководном приближении равна $\bar {u} = \frac{1}{8}\frac{{{{H}^{2}}}}{{{{h}^{2}}}}\sqrt {gh} $ [1]. При использовании формулы (9) после ряда преобразований найдем

(15)

$\begin{gathered} \frac{q}{L} = {{c}_{2}}{{\left( {gr} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{\left( {\frac{H}{{{{L}_{0}}}}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}}\frac{{{{H}^{{{{11} \mathord{\left/ {\vphantom {{11} 4}} \right. \kern-0em} 4}}}}}}{{{{h}^{{{{11} \mathord{\left/ {\vphantom {{11} 4}} \right. \kern-0em} 4}}}}}}, \\ {{c}_{2}} = \frac{{0.2{{{\left( 2 \right)}}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}}}{{{{\pi }^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}}}\frac{3}{{128}}\frac{{{{\varepsilon }_{b}}}}{{{\text{tg}}{{\alpha }_{g}}}}. \\ \end{gathered} $

Подставив (15) в (5), получим

(16)

$h = {{\left( {{{c}_{2}}\frac{{\Delta t}}{{\Delta h}}} \right)}^{{{4 \mathord{\left/ {\vphantom {4 {11}}} \right. \kern-0em} {11}}}}}{{\left( {gr} \right)}^{{{2 \mathord{\left/ {\vphantom {2 {11}}} \right. \kern-0em} {11}}}}}{{\left( {\frac{H}{{{{L}_{0}}}}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 {11}}} \right. \kern-0em} {11}}}}}H.$

Далее выразим $H$ через ${{H}_{0}}$ с помощью (12) и применим аппроксимацию ${{\left( {{H \mathord{\left/ {\vphantom {H {{{L}_{0}}}}} \right. \kern-0em} {{{L}_{0}}}}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 {11}}} \right. \kern-0em} {11}}}}} \approx {{\left( {{{{{H}_{0}}} \mathord{\left/ {\vphantom {{{{H}_{0}}} {{{L}_{0}}}}} \right. \kern-0em} {{{L}_{0}}}}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 {11}}} \right. \kern-0em} {11}}}}}$. Принимая длительность волнения $\Delta t$ = 12 ч, придем к соотношению для глубины замыкания:

(17)

${{h}_{*}} = {{K}_{2}}{{H}_{{s012}}},\,\,\,\,{{K}_{2}} = 2.46\frac{{{{r}^{{{2 \mathord{\left/ {\vphantom {2 {11}}} \right. \kern-0em} {11}}}}}}}{{\Delta {{h}^{{{4 \mathord{\left/ {\vphantom {4 {11}}} \right. \kern-0em} {11}}}}}}}{{\left( {\frac{{{{H}_{0}}}}{{{{L}_{0}}}}} \right)}^{{{4 \mathord{\left/ {\vphantom {4 {55}}} \right. \kern-0em} {55}}}}}{{H}_{{s012}}}.$

В условиях интенсивного транспорта наносов (sheet flow) параметр донной шероховатости $r$ в формулах (13) и (17) можно аппроксимировать соотношением [10]

(18)

$r = 15\Psi {{d}_{g}},$

где ${{d}_{g}}$ – размер частиц песка, $\Psi $ – параметр Шилдса порядка 1. Согласно (18), величина $r$ инвариантна к размеру частиц, так как, например, рост ${{d}_{g}}$ должен сопровождаться соответствующим уменьшением параметра $\Psi $ (который обратно пропорционален ${{d}_{g}}$). Полагая типичный размер песка за пределами зоны подводных валов равным ${{d}_{g}}$ = 0.15–0.25 мм и допуская $\Psi \approx 1$, получим из (18) среднюю оценку $r$ = 0.003 м, которую и будем использовать в дальнейшем. Возможные вариации $r$ не должны оказывать решающее влияние на конечный результат, поскольку ${{K}_{1}}$ и ${{K}_{2}}$ зависят от $r$ в сравнительно малой степени.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Таким образом, при заданном пороге деформаций $\Delta {{h}_{с}}$ фактор пропорциональности $K$ между глубиной замыкания и высотой волн зависит, главным образом, от крутизны волн ${{{{H}_{0}}} \mathord{\left/ {\vphantom {{{{H}_{0}}} {{{L}_{0}}}}} \right. \kern-0em} {{{L}_{0}}}}$. Это отражает рис. 3, где показаны изменения факторов ${{K}_{0}}$, ${{K}_{1}}$ и ${{K}_{2}}$, определяемые соотношениями (2), (13) и (17). Значения ${{K}_{1}}$ и ${{K}_{2}}$, отвечающие величине $\Delta {{h}_{с}}$ = 0.1 м, оказываются меньше ${{K}_{0}}$.

Рис. 3.

Фактор пропорциональности между глубиной замыкания ${{h}_{*}}$ и высотой волн ${{H}_{{s012}}}$ как функция крутизны волн: 1 – формула Халлермейера (${{K}_{0}}$); 2 – расчеты на основе принципа сохранения массы в условиях транспорта наносов за счет асимметрии волн (${{K}_{1}}$) и противотечения (${{K}_{2}}$); 3 – обобщенная зависимость ($\bar {K}$). Кривые ${{K}_{1}}$, ${{K}_{2}}$ и $\bar {K}$ отвечают порогу деформаций дна $\Delta {{h}_{с}}$ = 0.1 м.

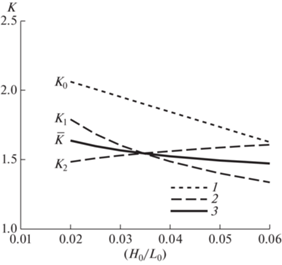
Очевидно, важную роль играет тип доминирующего механизма транспорта наносов – асимметрия волн или противотечение. В первом случае глубина ${{h}_{*}}$ с ростом крутизны волн уменьшается, что можно объяснить сдвигом области трансформации крутых волн ближе к берегу. В случае противотечения проявляется обратный тренд, обусловленный некоторым увеличением расхода наносов при действии относительно коротких волн. В реальных условиях оба отмеченных механизма транспорта могут играть одинаково важную роль. Поэтому для практической оценки глубины ${{h}_{*}}$, по-видимому, имеет смысл использовать среднюю величину фактора пропорциональности $\bar {K} = \frac{1}{2}({{K}_{1}} + {{K}_{2}})$. График $\bar {K}$, соответствующий $\Delta {{h}_{с}}$ = 0.1 м, также приведен на рис. 3.

Окончательную формулу глубины замыкания можно представить в виде

(19)

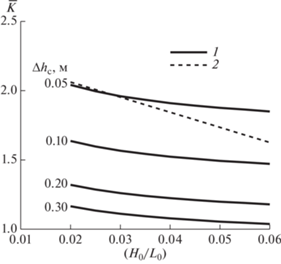
${{h}_{*}} = \bar {K}{{H}_{{s012}}},\,\,\,\,\bar {K} = \left[ {{{b}_{1}}{{{\left( {\frac{{{{H}_{0}}}}{{{{L}_{0}}}}} \right)}}^{{{{ - 4} \mathord{\left/ {\vphantom {{ - 4} {15}}} \right. \kern-0em} {15}}}}} + {{b}_{2}}{{{\left( {\frac{{{{H}_{0}}}}{{{{L}_{0}}}}} \right)}}^{{{4 \mathord{\left/ {\vphantom {4 {55}}} \right. \kern-0em} {55}}}}}} \right],$

где коэффициенты ${{b}_{1}}$ и ${{b}_{2}}$ зависят от заданной пороговой величины деформаций $\Delta {{h}_{с}}$, которая в различных исследованиях варьирует в диапазоне от 0.05 до 0.3 м:

$\begin{array}{*{20}{c}} {\Delta {{h}_{с}},\,\,{\text{м}}}&{0.05}&{0.10}&{0.20}&{0.30} \\ {{{b}_{1}}}&{0.39}&{0.32}&{0.26}&{0.24} \\ {{{b}_{2}}}&{1.27}&{0.99}&{0.77}&{0.66.} \end{array}$

Графики $\bar {K}$ при различных $\Delta {{h}_{с}}$ показаны на рис. 4 вместе с графиком фактора ${{K}_{0}}$ в формуле Халлермейера (2). Из представленных результатов следует, что при величине $\Delta {{h}_{с}}$ = 0.1 м глубина замыкания характеризуется значениями $(1.5~{\kern 1pt} - {\kern 1pt} 1.6){{H}_{{s012}}}$, а при увеличении порога деформаций до $\Delta {{h}_{с}}$ = 0.3 м глубина ${{h}_{*}}$ уменьшается до значений $(1.1~{\kern 1pt} - {\kern 1pt} 1.2){{H}_{{s012}}}$.

Рис. 4.

Фактор пропорциональности $\bar {K}$ в формуле (19) как функция крутизны волн при различных значениях порога деформаций дна $\Delta {{h}_{с}}$ (1), а также соответствующий фактор ${{K}_{0}}$ в формуле Халлермейера (2).

Вместе с тем, при величине $\Delta {{h}_{с}}$ = 0.05 м расчеты по зависимостям (19) и (2) дают весьма близкие результаты. Это означает, что формула Халлермейера, по существу, соответствует довольно низкому порогу деформаций, маркирующему границу активного профиля. Поэтому сопоставление (2) с данными исследований, в которых используется более высокий порог $\Delta {{h}_{с}}$, не дает положительных результатов.

На рис. 5 полученная зависимость (19) сравнивается с эмпирической формулой (3), которая в данном случае экстраполирована в область больших высот волн. Как видно, в интервале ${{H}_{{s012}}}$ до 4–5 м формула (3) дает более высокие значения ${{h}_{*}}$. Для самых крупных волн, наоборот, более высокие значения предсказывает формула (19). Примечательно, что на изменение порога деформаций $\Delta {{h}_{с}}$ обе зависимости реагируют примерно одинаковым образом.

Рис. 5.

Сравнение формул (19) и (3) при различных значениях порога деформаций дна $\Delta {{h}_{с}}$: 1 – аналитическая зависимость (19) при крутизне волн 0.04; 2 – эмпирическая зависимость (3).

СРАВНЕНИЕ РАСЧЕТОВ С НАБЛЮДЕНИЯМИ

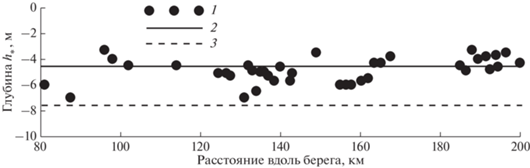
На рис. 6 результаты расчетов сравниваются с данными наблюдений в Лионском заливе (западная часть средиземноморского побережья Франции), где распространены относительно пологие песчаные берега с сериями подводных валов. Исследование [15] включало повторные промеры дна в течение 4 лет на нескольких десятках профилей, расположенных на 170-километровом участке побережья. С учетом точности измерений, порог деформаций дна при определении глубины замыкания принимался равным $\Delta {{h}_{с}}$ = = 0.3 м.

Рис. 6.

Сравнение расчетов глубины замыкания с данными натурных наблюдений [15]. 1 – Результаты промеров; 2 – расчеты по формуле (19) при $\Delta {{h}_{с}}$ = 0.3 м; 3 – расчеты по формуле (2).

Прилив в рассматриваемом регионе довольно мал (до 0.3 м), а доминирующее волнение ЮВ румба характеризуется высотой ${{H}_{{s012}}}$ = 4.10 м и ассоциированным периодом $T$ = 8.08 с [15]. Крутизна таких волн составляет ${{{{H}_{0}}} \mathord{\left/ {\vphantom {{{{H}_{0}}} {{{L}_{0}}}}} \right. \kern-0em} {{{L}_{0}}}}$ = 0.040, и расчет по формуле (19) дает величину ${{h}_{*}}$ = 4.43 м.

Как видно на рис. 6, измеренная глубина замыкания обнаруживает значительную изменчивость по протяжению берега, обусловленную локальными неоднородностями рельефа дна и береговой линии. Глубина ${{h}_{*}}$, предсказанная формулой (2), как и ожидалось, находится за пределами всех измеренных величин. К сожалению, в данном случае нет возможности проверить формулу (3), диапазон которой ограничивается значениями $\Delta {{h}_{с}} \leqslant $ 0.2 м. Вместе с тем очевидно, что значение ${{h}_{*}}$, рассчитанное по формуле (19), оказывается достаточно репрезентативным усредненным показателем глубины замыкания в рассматриваемом регионе.

Еще один пример сравнения основан на данных упомянутого ранее исследования [4], проводившегося на средиземноморском побережье Испании в районе Валенсии (прилив здесь почти не выражен). Глубина замыкания определялась как на базе повторных промеров дна (при $\Delta {{h}_{с}}$ = 0.3 м), так и с помощью анализа распределения крупности песка по профилю берега. Это привело к оценке ${{h}_{*}}$ в интервале от 4.0 до 4.8 м. Доминирующее волнение в рассматриваемом регионе характеризовалось высотой ${{H}_{{s012}}}$ = 3.77 м и ассоциированным периодом $T$ = 12.3 с [4], что соответствовало крутизне ${{{{H}_{0}}} \mathord{\left/ {\vphantom {{{{H}_{0}}} {{{L}_{0}}}}} \right. \kern-0em} {{{L}_{0}}}}$ = 0.016. Расчет по формуле Халлермейера (2) дает сильно завышенную величину ${{h}_{*}}$ = 7.9 м, тогда как глубина замыкания, рассчитанная по формуле (19), оценивается значением ${{h}_{*}}$ = 4.53 м, близким к среднему результату измерений.

ЗАКЛЮЧЕНИЕ

Глубина замыкания ограничивает область существенных морфологических изменений дна, фиксируемых при повторных промерах в течение периода времени порядка года. Для аналитического определения данной границы необходимо принимать в расчет не только интенсивность транспорта наносов, но и его градиент, который, собственно, и служит причиной наблюдаемых штормовых деформаций берегового профиля. Связь между градиентом расхода наносов и деформациями дна $\Delta h$ устанавливается принципом сохранения массы. Его применение позволяет найти глубину $h$, на которой при действии данного волнения в течение заданного времени будет достигнута заданная величина деформаций дна.

Транспорт наносов в данной работе трактуется с позиций энергетической концепции [5, 7]. Принимаются во внимание два главных механизма, вызывающих поперечное перемещение наносов в береговой зоне – асимметрия волновых скоростей и противотечение. В результате при использовании ряда приближений и параметризаций получена формула, определяющая глубину замыкания ${{h}_{*}}$ в зависимости от высоты штормовых волн ${{H}_{{s012}}}$, превышение которых возможно не более 12 ч в году.

Фактор пропорциональности между ${{h}_{*}}$ и ${{H}_{{s012}}}$ зависит от крутизны волн (с ее ростом ${{h}_{*}}$ немного уменьшается), а также от заданного порога деформаций дна $\Delta {{h}_{с}}$, который при натурных исследованиях определяется точностью промеров глубин. Чем больше принятое значение $\Delta {{h}_{с}}$, тем меньше глубина ${{h}_{*}}$ и ширина активной области берегового профиля. При типичных значениях $\Delta {{h}_{с}}$ от 0.1 до 0.3 м глубина замыкания оценивается величинами от $(1.5~{\kern 1pt} - {\kern 1pt} 1.6){{H}_{{s012}}}$ до $(1.1~{\kern 1pt} - {\kern 1pt} 1.2){{H}_{{s012}}}$.

Полученные результаты показывают, что широко известная формула Халлермейера [12] отвечает довольно низкому порогу деформаций (около 0.05 м), что объясняет завышение расчетных значений ${{h}_{*}}$ по сравнению с измеренными, которые соответствуют, как правило, более высокому порогу $\Delta {{h}_{с}}$.

Сравнение полученных результатов с данными наблюдений показывает, что оценка ${{h}_{*}}$ на основе предложенной формулы (19) может служить репрезентативным показателем глубины замыкания на песчаных берегах с небольшой высотой прилива. В дальнейшем планируется верификация результатов расчетов в более широком диапазоне условий прибрежной среды.

Источник финансирования. Работа выполнена в рамках государственного задания ИО РАН (тема № 0128-2021-0004) при частичной поддержке РФФИ (грант № 18-55-34 002 Куба_т).

Список литературы

Леонтьев И.О. Прибрежная динамика: волны, течения, потоки наносов. М.: ГЕОС, 2001. 272 с.
Леонтьев И.О. Морфодинамические процессы в береговой зоне моря. Saarbrücken: LAP LAMBERT Academic Publishing, 2014. 251 с.
Леонтьев И.О. Искусственный пляж как средство защиты берегов от штормовых нагонов (на примере восточной части Финского залива) // Океанология. 2019. Т. 59. № 2. С. 292–301.
Aragonés L., Pagán J.I., López I., Serra J.C. Depth of closure: new calculation method based on sediment data // Int. Journal of Sediment Research. 2018. V. 33. № 2. P. 198–207.
Bailard J.A. An energetics total load sediment transport model for a plane sloping beach // J. of Geophys. Res. 1981. V. 86. № C11. P. 10 938–10 954.
Birkemeier W.A. Field data on seaward limit of profile change // J. of Waterway, Port, Coastal and Ocean Engineering. 1985. V. 111. № 3. P. 598–602.
Bowen A.J. Simple models of nearshore sedimentation; beach profiles and longshore bars // The Coastline of Canada / Ed. S. B. McCann. Geological Survey of Canada. Halifax, 1980. P. 1–11.
Bruun P. The Bruun rule of erosion by sea-level rise: a discussion on large-scale two- and three-dimensional usages // J. of Coastal Res. 1988. V. 4. № 4. P. 627–648.
Capobianco M., Larson M., Nicholls R.J. Kraus N.C. Depth of closure: a contribution to the reconcillation of theory, practice and evidence // Int. Conference “Coastal Dynamics’97”. Plymouth. 1997. P. 506–515.
Coastal Engineering Manual. EM 1110-2-1100. Part III– Chap. 6. US Army Corps of Engineers. Washington D.C. 2002.
Dean R.G. Beach nourishment: theory and practice. World Scientific Inc. 2002. 399 p.
Hallermeier R.J. Uses for a calculated limit depth to beach erosion // Proc. 16^th Coastal Engineering Conference. ASCE. New York. 1978. V. 2. P. 1493–1512.
Hanson H. GENESIS: a generalized shoreline change numerical model // J. of Coastal Res. 1989. V. 5. № 1. P. 1–27.
Nicholls R.J., Birkemeier W.A., Lee G. Evaluation of depth of closure using data from Duck, NC, USA // Marine Geol. 1998. V. 148. P. 178–191.
Sabatier F., Stive M.J.F., Pons F. Longshore variation of depth of closure on a micro-tidal wave-dominated coast // Proc. 29^th Int. Conference on Coastal Engineering. ASCE. New York. 2004. V. 3. P. 2327–2339.
Soulsby R.L. Dynamics of marine sands. London: Thomas Telford, 1997. 249 p.
Van Rijn L.C., Tonnon P.K., Walstra D.J.R. Numerical modeling of erosion and accretion of plane sloping beaches at different scales // Coastal Engineering. 2011. V. 58. P. 637–655.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Океанология

Архивы выпусков Информация о журнале Отправить рукопись в журнал