Океанология, 2022, T. 62, № 3, стр. 341-356
Особенности формирования поля плотности в мезомасштабных вихрях Лофотенской котловины. Часть 2
В. В. Жмур 1, 2, Е. В. Новоселова 1, *, Т. В. Белоненко 1
1 Санкт-Петербургский государственный университет
Санкт-Петербург, Россия
2 Институт океанологии им. П.П. Ширшова РАН
г. Москва, Россия
* E-mail: e.novoselova@spbu.ru
Поступила в редакцию 27.09.2021
После доработки 16.12.2021
Принята к публикации 25.02.2022
- EDN: ESVALE
- DOI: 10.31857/S0030157422030170
Аннотация
Эта статья продолжает исследования авторов об изменениях частоты Вяйсяля-Брента, вызванных мезомасштабными вихрями различной полярности. Если в первой части обсуждались теоретические выводы, то во второй части дается интерпретация этих результатов на основе натурных данных. Район исследования – Лофотенская котловина Норвежского моря. Для анализа используются данные океанического реанализа GLORYS12V1 за 10 июня 2010 г. Рассматриваются два вихря: квазипостоянный антициклон – Лофотенский вихрь (ЛВ), расположенный в центре котловины, и циклон, расположенный юго-восточнее ЛВ. Проверяются математические формулы, вычисляются характеристики вихрей, исследуются профили и вертикальные разрезы потенциальной завихренности и частоты Вяйсяля-Брента. На основе совместного анализа натурного и теоретического материала косвенно оценены свойства рассмотренных вихрей, которые невозможно измерить непосредственно и нельзя получить в моделях.
1. ВВЕДЕНИЕ
Лофотенская котловина представляет собой понижение в рельефе дна Норвежского моря с максимальной глубиной 3250 м и ограничена координатами 5° з.д.–20° в.д. и 64°–76° с.ш. [1]. Будучи обособленным топографическим образованием, котловина расположена между хребтом Мона на северо-западе и Скандинавским полуостровом на востоке, с юга она ограничена плато Воринг (рис. 1). Лофотенская котловина является одним из динамически активных районов Мирового океана и характеризуется повышенной вихревой активностью. Основными элементами циркуляции в регионе являются ветви Норвежского течения: Склоновое, Фронтальное и Прибрежное. Ввиду неустойчивости этих течений возникают условия для образования мезомасштабных вихрей [22, 23], которые, отрываясь от струи течения, перемещаются в котловине под влиянием топографических уклонов и β-эффекта, образуя несколько основных “коридоров” их перемещения [13, 17, 27 ].
Для исследования изменений частоты Вяйсяля-Брента (ВБ) в циклонах и антициклонах выбраны два вихря, на рис. 2a показано их расположение. Изменения частоты ВБ в вихрях анализировались относительно так называемой фоновой частоты ВБ N0 (или частоты ВБ в покое). Отметим, что выбор подходящего профиля не является простой задачей: на рис. 2б видно, что котловина “усеяна” мезомасштабными вихрями. Действительно, алгоритм автоматической идентификации и трекинга вихрей, примененный к спутниковым альтиметрическим данным, позволил обнаружить в Лофотенской котловине за период с 1993 по 2017 гг. проявление 166 000 циклонических и 169 395 антициклонических вихрей. Вихри перераспределяют тепло и соль по акватории котловины [15], тем самым оказывая значительное влияние в том числе и на изменения частоты ВБ. Будучи транзитной зоной для теплых и соленых атлантических водных масс на их пути в Северный Ледовитый океан, Лофотенская котловина играет важную роль в поддержании глобальной Меридиональной термохалинной циркуляции в области, где атлантические водные массы отдают тепло в атмосферу, перемешиваются с окружающими водами и претерпевают трансформацию, необходимую для образования глубинных вод [8, 9]. Анализ мезомасштабной динамики, который проводился по трекам долгоживущих (время жизни более 35 суток) вихрей, позволил выявить в котловине 120 циклонических и 210 антициклонических индивидуальных вихрей, связанных в треки [27]. При этом обнаружено, что в Лофотенской котловине могут существовать по крайней мере два механизма вихреобразования: это либо отрыв меандров от струи Норвежского течения, либо генерация вихрей на склонах котловины, где скорость течения невелика [12, 17, 24 ].
Рис. 2.
Аномалии уровня, м (a) и относительная завихренность на глубине 100 м, с–1 (б). Черными кругами показаны выбранные циклон (точками) и антициклон (штрихом). Черным крестиком обозначено расположение точки с профилем фоновой частоты Вяйсяля-Брента.
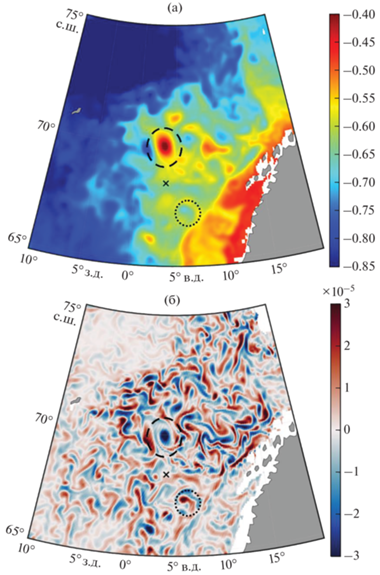
Квазипостоянный антициклонический Лофотенский вихрь (ЛВ) является примечательной особенностью котловины [2, 7, 24]. Зимняя конвекция способствует существованию этого уникального природного феномена, создавая благоприятные условия его ежегодной регенерации [10, 11 ]. Другим механизмом, позволяющим поддерживать в центре котловины высокую антициклоническую завихренность, является слияние с мезомасштабными антициклоническими вихрями, отрывающимися от Норвежского течения [16]. Известно, что в окрестности крупных антициклонов часто существуют устойчивые циклонические образования, так называемые ринглеты [19] (см. также [3, 5, 6, 20, 21 ]). Действительно, в окрестности ЛВ также часто образуются циклоны, которые совместно с Лофотенским антициклоном образуют систему совместно вращающихся вихрей [14].
Растяжение или сжатие по вертикали элементарных жидких объемов приводит к изменениям частоты ВБ. В данной работе на основе эмпирических данных рассматривается воздействие мезомасштабных вихрей океана на перестройку частоты ВБ, которая возрастает при усилении стратификации морской воды и уменьшается в слабостратифицированных водах. Наличие вихрей приводит к деформации и смещению изопикн, которые в покоящемся океане при отсутствии вихрей представляют собой горизонтальные поверхности, причем наиболее сильной деформации будут подвергаться те части изопикнических поверхностей, которые попали внутрь вихревого ядра или находятся вблизи него. В настоящей работе использованы подходы, изложенные в первой части статьи [26]. Целью исследования является верификация полученных ранее выводов, а также оценка изменений частоты ВБ, связанных с воздействием мезомасштабных вихрей океана на стратификацию вод.
2. МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ: ПОТЕНЦИАЛЬНАЯ ЗАВИХРЕННОСТЬ, ПОЛЕ ПЛОТНОСТИ И ЧАСТОТА ВЯЙСЯЛЯ-БРЕНТА. ОСНОВНЫЕ ФОРМУЛЫ
Мы будем исходить из справедливости квазигеострофического подхода к описываемым явлениям, при котором должен выполняться закон сохранения потенциального вихря для движущейся жидкой частицы. Ниже для целостности изложения приводятся математические соотношения, которые будут использованы для оценок различных физических параметров вихрей [26].
В системе координат с двумя горизонтальными осями $\left( {x,y} \right)$ и вертикальной осью $z$ потенциальная завихренность $\sigma $ выражается через функцию тока $\psi \left( {x,y,z,t} \right)$ ($t$ – время, $f$ – параметр Кориолиса) [4]:
(1)
$\sigma = {{\Delta }_{h}}\psi \left( {x,y,z,t} \right) + \frac{\partial }{{\partial z}}\frac{{{{f}^{2}}}}{{{{N}^{2}}}}\frac{{\partial \psi \left( {x,y,z,t} \right)}}{{\partial z}}.$(2)
$\sigma = {\text{ro}}{{{\text{t}}}_{z}}\vec {u} + \frac{{{{\partial }^{2}}\psi \left( {x,y,\tilde {z},t} \right)}}{{\partial {{{\tilde {z}}}^{2}}}},$Если первоначально покоящуюся жидкость с постоянной частотой ВБ ${{N}_{0}}$ привести в движение, описываемое функцией тока $\psi \left( {x,y,\tilde {z},t} \right)$, то новое распределение ${{N}^{2}}\left( {x,y,z,t} \right)~~$ примет вид:
(3)
${{N}^{2}}\left( {x,y,z,t} \right) = N_{0}^{2}\left\{ {1 + \frac{1}{f}\frac{{{{\partial }^{2}}\psi \left( {x,y,\tilde {z},t} \right)}}{{\partial {{{\tilde {z}}}^{2}}}}} \right\}.$Для эллипсоидальных ядер вихрей (в терминологии [26]), однородных по потенциальной завихренности, получаем:
(4)
${\text{ro}}{{{\text{t}}}_{z}}\vec {u} = \frac{1}{2}\sigma K\mathop \smallint \limits_0^\infty \frac{{\left( {2\tilde {\mu } + \nu } \right)d\tilde {\mu }}}{{{{{\left( {{{K}^{2}} + \tilde {\mu }} \right)}}^{{\frac{1}{2}}}}{{{\left( {{{{\tilde {\mu }}}^{2}} + \nu \tilde {\mu } + 1} \right)}}^{{\frac{3}{2}}}}}}~,$(5)
$\frac{{{{\partial }^{2}}\psi }}{{\partial {{{\tilde {z}}}^{2}}}} = \frac{1}{2}\sigma K\mathop \smallint \limits_0^\infty \frac{{d\tilde {\mu }}}{{{{{\left( {{{K}^{2}} + \tilde {\mu }} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{{\left( {{{{\tilde {\mu }}}^{2}} + \nu \tilde {\mu } + 1} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}},$(6)
$\nu = \frac{a}{b} + \frac{b}{a},\,\,\,\,~K = \frac{{\tilde {c}}}{{\sqrt {ab} }} = \frac{{{{N}_{0}}}}{f}\frac{c}{{\sqrt {ab} }}.$Следует отметить, что постоянные характеристики ядра вихря ${\text{ro}}{{{\text{t}}}_{z}}\vec {u}$ и $\frac{{{{\partial }^{2}}\psi }}{{\partial {{{\tilde {z}}}^{2}}}}$ – одного знака, совпадающего со знаком потенциальной завихренности ядра $\sigma $, и связаны между собой соотношением (2). Это означает, что каждое из выражений $\frac{{{\text{ro}}{{{\text{t}}}_{z}}\vec {u}}}{\sigma }$ и $\frac{1}{\sigma }\frac{{{{\partial }^{2}}\psi }}{{\partial {{{\tilde {z}}}^{2}}}}~$ меняется в диапазоне от нуля до единицы в зависимости от значений $\nu $ и $K$. Увеличение одного приводит к уменьшению другого, и наоборот. Однако перераспределение первоначально постоянной частоты ВБ (3) связано только с $\frac{{{{\partial }^{2}}\psi }}{{\partial {{{\tilde {z}}}^{2}}}}~$ и не зависит от ${\text{ro}}{{{\text{t}}}_{z}}\vec {u}$. Поэтому следует ожидать, что деформация частоты ВБ будет сильнее у вихрей с максимально большим значением $\frac{1}{\sigma }\frac{{{{\partial }^{2}}\psi }}{{\partial {{{\tilde {z}}}^{2}}}}$. Как будет показано ниже, это условие выполняется для тонких осесимметричных вихрей с $\nu = 2$ и $K \ll 1$.
Применяемая здесь теория эллипсоидальных вихрей основана на двух предположениях: однородной потенциальной завихренности всех частиц вихревого ядра $\sigma $ и эллипсоидальности формы ядра. В реальности эти свойства вихрей нарушаются, однако при этом закон сохранения потенциальной завихренности частиц (1) и (2) остается в силе. Это дает возможность перейти к средним по объему ядра вихря характеристикам ${\text{ro}}{{{\text{t}}}_{z}}\vec {u}$, $\frac{\partial }{{\partial z}}\frac{{{{f}^{2}}}}{{N_{0}^{2}\left( z \right)}}\frac{{\partial \psi \left( {x,y,z,t} \right)}}{{\partial z}}$ и $\sigma $, которые связаны соотношением
(7)
${\text{ro}}{{{\text{t}}}_{z}}\vec {u} + \frac{\partial }{{\partial z}}\frac{{{{f}^{2}}}}{{N_{0}^{2}\left( z \right)}}\frac{{\partial \psi \left( {x,y,z,t} \right)}}{{\partial z}} = \sigma {\text{,}}$(8)
$\frac{\partial }{{\partial z}}\frac{{{{f}^{2}}}}{{N_{0}^{2}\left( z \right)}}\frac{{\partial \psi \left( {x,y,z,t} \right)}}{{\partial z}} = \varepsilon \sigma {\text{,}}\,\,\,\,{\text{ro}}{{{\text{t}}}_{z}}\vec {u} = \left( {1 - \varepsilon {\text{\;}}} \right)\sigma .$(9)
$\varepsilon = \frac{1}{2}K\mathop \smallint \limits_0^\infty \frac{{d\tilde {\mu }}}{{{{{\left( {{{K}^{2}} + \tilde {\mu }} \right)}}^{{\frac{3}{2}}}}{{{\left( {{{{\tilde {\mu }}}^{2}} + \nu \tilde {\mu } + 1} \right)}}^{{\frac{1}{2}}}}}}.$В теории также не учитывалась возможность водообмена вихревого ядра с внешним водным пространством. В реальности присутствует и то, и другое. Все это может сильнейшим образом перестроить указанные частоты $N_{{{\text{min}}}}^{2}$ и $N_{{\max }}^{2}$. Поэтому при изучении реальной трансформации поля частоты ВБ вихрями мы будем учитывать полученные ограничения качественно. В частности, можно ожидать, что у достаточно интенсивных антициклонов вихревые ядра будут полностью однородны по плотности, а сгущение “вытолкнутых” из ядра изопикн образуют над и под ядром зоны значительно повышенных частот ВБ. Для циклонов общим выводом служит более скромное свойство – с увеличением интенсивности циклона в вихревых ядрах максимально наблюдаемая частота ВБ должна нарастать, а значение $N_{{\max }}^{2}$ ограничено сверху.
Соотношение (3) представляет собой выражение для поля деформированной вихрем ${{N}^{2}}\left( {x,y,z,t} \right)$ первоначально постоянной $N_{0}^{2}~$ частоты ВБ при отсутствии внешних фоновых течений. В случае эллипсоидальных вихрей при тех же условиях (3) преобразуется в точное выражение
(10)
$\begin{gathered} {{N}^{2}} = N_{0}^{2}\left\{ {1 + \frac{\varepsilon }{{1 - \varepsilon }}\frac{{{\text{ro}}{{{\text{t}}}_{z}}\vec {u}}}{f}} \right\} = \\ = N_{0}^{2}\left\{ {1 + {\text{sign}}\left( \sigma \right)\frac{\varepsilon }{{1 - \varepsilon }}{\text{Ro}}} \right\}, \\ \end{gathered} $В работе мы будем рассчитывать распределение потенциальной завихренности в вихрях по натурным данным с использованием предположения о постоянстве ${{N}_{0}}~$ и переменной $N\left( z \right)~$ частоты ВБ по формулам (1) и (2). Обсуждение такого подхода при оценке слагаемого $\frac{1}{f}\frac{\partial }{{\partial z}}$ × × $\frac{{{{f}^{2}}}}{{N_{0}^{2}\left( z \right)}}\frac{{\partial \psi \left( {x,y,z,t} \right)}}{{\partial z}}$ будет приведено ниже. В [26] обсуждался вариант оценки этого же слагаемого через сравнение вертикальных распределений поля плотности в ядре вихря и зоне покоя, где можно пренебречь движением воды. В результате получено два полезных соотношения. Первое – можно получить простую оценку слагаемого $\frac{1}{f}\frac{\partial }{{\partial z}}\frac{{{{f}^{2}}}}{{N_{0}^{2}\left( z \right)}}\frac{{\partial \psi \left( {x,y,z,t} \right)}}{{\partial z}}$ для выбранного горизонта:
(11)
$\begin{gathered} \frac{1}{f}\frac{\partial }{{\partial z}}\frac{{{{f}^{2}}}}{{N_{0}^{2}\left( z \right)}}\frac{{\partial \psi \left( {x,y,z,t} \right)}}{{\partial z}} = \\ = \frac{{{{N}^{2}}\left( {x,y,z,t} \right) - N_{0}^{2}\left( z \right)}}{{N_{0}^{2}\left( z \right)}} - \\ - \,\,\frac{g}{{{{\rho }_{*}}}}\left( {\rho \left( {x,y,z,t} \right) - {{\rho }_{0}}\left( z \right)} \right)\frac{\partial }{{\partial z}}\left\{ {\frac{1}{{N_{0}^{2}\left( z \right)}}} \right\}, \\ \end{gathered} $Второе – вычисляя среднее значение $\frac{1}{f}\frac{\partial }{{\partial z}}\frac{{{{f}^{2}}}}{{N_{0}^{2}\left( z \right)}}\frac{{\partial \psi \left( {x,y,z,t} \right)}}{{\partial z}}$ по слою жидкости между глубинами ${{h}_{1}}$ и ${{h}_{2}}$, получим в тех же обозначениях следующее соотношение:
(12)
$\begin{gathered} \left\langle {\frac{1}{f}\frac{\partial }{{\partial z}}\frac{{{{f}^{2}}}}{{N_{0}^{2}\left( z \right)}}\frac{{\partial \psi \left( {x,y,z,t} \right)}}{{\partial z}}} \right\rangle _{{{{h}_{1}}}}^{{{{h}_{2}}}} = \\ = - \frac{g}{{{{\rho }_{*}}}}\frac{1}{{{{h}_{2}} - {{h}_{1}}}}\left\{ {\frac{1}{{N_{0}^{2}\left( {{{h}_{2}}} \right)}}\left( {\rho (x,y,{{h}_{2}},t} \right) - {{\rho }_{0}}\left( {{{h}_{2}}} \right))} \right. - \\ \left. { - \,\,\frac{1}{{N_{0}^{2}\left( {{{h}_{1}}} \right)}}\left( {\rho (x,y,{{h}_{1}},t} \right) - {{\rho }_{0}}\left( {{{h}_{1}}} \right))} \right\}, \\ \end{gathered} $(13)
$\begin{gathered} \sigma = \left\langle {{\text{ro}}{{{\text{t}}}_{z}}u} \right\rangle _{{{{h}_{1}}}}^{{{{h}_{2}}}} - \\ - \,\,f\frac{g}{{{{\rho }_{*}}}}\frac{1}{{{{h}_{2}} - {{h}_{1}}}}\left\{ {\frac{1}{{N_{0}^{2}\left( {{{h}_{2}}} \right)}}\left( {\rho \left( {x,y,{{h}_{2}},t} \right) - {{\rho }_{0}}\left( {{{h}_{2}}} \right)} \right)} \right. - \\ \left. { - \,\,\frac{1}{{N_{0}^{2}\left( {{{h}_{1}}} \right)}}\left( {\rho \left( {x,y,{{h}_{1}},t} \right) - {{\rho }_{0}}\left( {{{h}_{1}}} \right)} \right)} \right\}. \\ \end{gathered} $3. ДАННЫЕ
Мы использовали данные GLORYS12V1, доступные на сайте CMEMS (Copernicus Marine Environment Monitoring Service) по ссылке http:// marine.copernicus.eu. GLORYS12V — глобальный океанический вихреразрешающий реанализ, основанный на модели NEMO, разработанный с использованием атмосферного реанализа ECMWF ERA-Interim. Начальные условия для температуры и солености взяты из данных EN.4.2.0 Hadley Center для 1991 г. Неоспоримым преимуществом реанализа GLORYS12V1 является ассимиляция спутниковых и in situ данных. В частности, более 5000 профилей поплавков Argo ассимилированы в этом продукте. Ассимилируются также вдольтрековые аномалии уровня моря (SLA, Sea Level Anomalies), температура поверхности моря (SST, Sea Surface Temperature), а также профили температуры и солености из базы данных CMEMS CORAv4.1, начиная с 2005 г. Для ассимиляции применяется фильтр Калмана. Данные о температуре и солености на 50 горизонтах с пространственным разрешением (1/12)°, что составляет приблизительно 4 × 8 км для высоких широт, доступны с ежесуточной и месячной дискретностью. Для верификации в работе мы использовали данные на 50 горизонтах за 10 июня 2010 г.
Профили частоты ВБ рассчитывались с помощью термодинамического уравнения TEOS-10 [18], реализованного в среде Matlab. Потенциальная завихренность рассчитывалась по формуле (1). Несмотря на то, что частота ${{N}^{2}}$ стоит в знаменателе, для расчетов это не создает проблем, так как близкие к нулю значения частоты ВБ присутствуют только в верхнем квазиоднородном слое, а нулевые значения отсутствуют.
4. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЦИКЛОНА
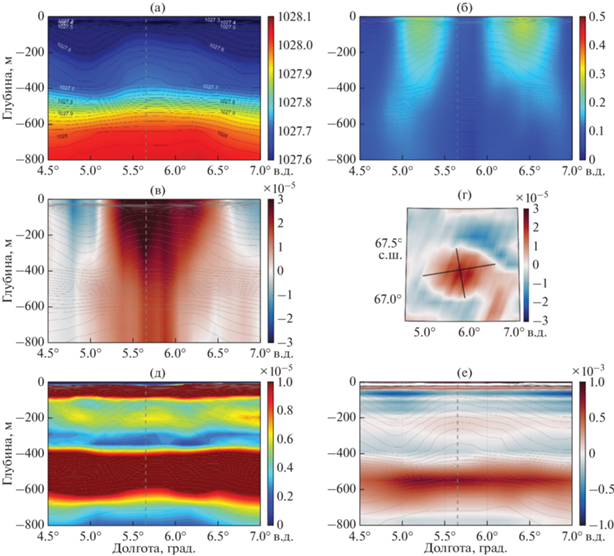
На рис. 3a видно, что анализируемый циклон (рис. 2б) является подповерхностным, при этом в слое до ≈ 450 м прогиб изопикн к поверхности достигает 100 м. Динамический сигнал вихря, обнаруживаемый в орбитальных скоростях, проявляется и в более глубоких слоях, превышающих 1000 м. Орбитальные скорости в циклоне достигают 30 см/с (рис. 3б). Максимальные значения относительной завихренности ${\text{ro}}{{{\text{t}}}_{z}}\vec {u}$ отмечаются до 500 м (рис. 3в). На горизонте 417 м пространственные масштабы циклона, определяемые по границе с нулевой относительной завихренностью, составляют 72.3 км длины и 48.8 км ширины с эффективным горизонтальным размером ${{L}_{{{\text{eff}}}}} = \sqrt {ab} = 59.4$ км (рис. 3г) [4]. Потенциальная завихренность $\sigma $ имеет максимальные значения порядка 1.0 × 10–3 с–1 в области сгущения изопикн под ядром циклона и отчасти в верхнем подповерхностном слое. Максимальные изменения частоты ВБ соответствуют слою от 100 до 400 м (рис. 3д). Две области сгущения изопикн в верхнем слое и на глубине 400–600 м соответствуют двум областям повышенных значений N 2. Ниже подповерхностного слоя значения $\sigma $ отрицательные; на рисунке как положительные, так и отрицательные экстремальные значения имеют порядок 1.0 × 10–4 с–1 (рис. 3е). Видно, что основной вклад в $\sigma $ дает слагаемое $\frac{\partial }{{\partial z}}\frac{{{{f}^{2}}}}{{N_{0}^{2}\left( z \right)}}\frac{{\partial \psi \left( {x,y,z,t} \right)}}{{\partial z}}$.
Рис. 3.
Циклон: потенциальная плотность, кг/м3 (a); орбитальная скорость, м/с (б); относительная завихренность ${\text{ro}}{{{\text{t}}}_{z}}\vec {u}$, с–1 (в); относительная завихренность на горизонте 417 м, оси эллипса показаны черными линиями (г); квадрат частоты Вяйсяля-Брента, с–2 (д); потенциальная завихренность $\sigma $, с–1 (е). Серыми линиями нанесены изопикны. Вертикальной пунктирной линией отмечен центр вихря. Вертикальные разрезы проведены через 67.25° с.ш. Серая штриховая линия проходит через центр вихря.
5. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ АНТИЦИКЛОНА
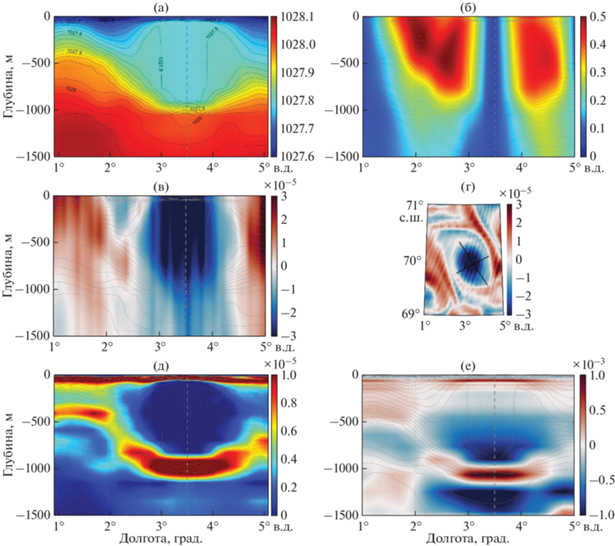
Антициклонический Лофотенский вихрь является мощным динамическим образованием (рис. 4a), динамический сигнал которого распространяется до самого дна [25]. Изменение термохалинных характеристик преимущественно отмечается в слое до 1000 м, а ядро расположено в слое 100–800 м. В работах [1, 2, 23 ] отмечалось расположение ядра на глубинах 200–800 м. Орбитальные скорости в антициклоне превышают 50 см/с (рис. 4б). Относительная завихренность максимальна (по модулю) в ядре (рис. 4в), но динамический сигнал (отрицательные значения относительной завихренности) прослеживается до самого дна (3250 м). На рис. 4г видно, что масштабы антициклона существенно превышают масштабы циклона не только по вертикали, но и по горизонтали: a = 108.7 км, b = 67.9 км с эффективным горизонтальным размером ${{L}_{{{\text{eff}}}}} = \sqrt {ab} = 85.9$ км. Ядро вихря хорошо выделяется на разрезе частоты ВБ (рис. 4д), при этом в слоях над и под ядром, где наблюдается сгущение изопикн, значения частоты ВБ положительны и максимальны, а в самом ядре – почти везде нулевые. Разрез потенциальной завихренности (рис. 4е) внешне похож на график частоты ВБ, а максимальные положительные значения $\sigma $ соответствуют областям сгущения изопикн и достигают 1.0 × 10–3 с–1. Минимальные отрицательные значения расположены в прилегающих слоях, значения составляют –1.0 × × 10–3 с–1. Сравнение разрезов ${\text{ro}}{{{\text{t}}}_{z}}\vec {u}$ и $\sigma $ показывает, что основной вклад в $\sigma $ также дает слагаемое $\frac{\partial }{{\partial z}}\frac{{{{f}^{2}}}}{{N_{0}^{2}\left( z \right)}}\frac{{\partial \psi \left( {x,y,z,t} \right)}}{{\partial z}}$.
Рис. 4.
Антициклон: (a), (б), (в) – проходящие через ось антициклона вертикальные разрезы полей потенциальной плотности (кг/м3), орбитальной скорости (м/с), относительной завихренности ${\text{ro}}{{{\text{t}}}_{z}}\vec {u}$ (с–1) соответственно; (г) – горизонтальный разрез на глубине 417 м относительной завихренности, оси эллипса изображены черными линиями; (д) – квадрат частоты Вяйсяля-Брента, с–2; (е) – потенциальная завихренность $\sigma $, с–1. Серыми линиями нанесены изопикны. Вертикальные разрезы проведены через 67.25° с.ш. Серая штриховая линия проходит через центр вихря.
При изучении полей относительной завихренности циклона и антициклона обращает на себя внимание наличие “столба” вращающейся жидкости под ядрами вихревых образований. Это можно наблюдать на рис. 3в и 4в. Судя по тому, что “столбы” протянулись от нижней границы вихревых ядер до дна, можно сделать вывод о баротропном происхождении этого явления. По всей видимости, эти “вращающиеся столбы” образовались в результате отклика океана на искривление вихрями уровня поверхности моря и неполной компенсации полученных скоростей смещением изопикн в толще моря.
6. ПРОФИЛИ ЧАСТОТЫ ВЯЙСЯЛЯ-БРЕНТА
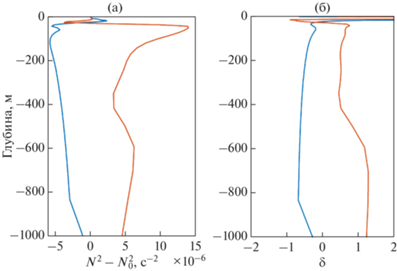
Профили частоты ВБ в вихрях и соответствующие аномалии относительно фоновой частоты представлены на рис. 5. Видно, что экстремумы достигаются в верхнем 50-метровом слое. В ядре циклона в слое 100–400 м отмечается максимум аномалий частоты ВБ с положительными значениями аномалий. Это связано с прогибом изопикн к поверхности. Другой максимум расположен на горизонте 500 м, где происходит сгущение изопикн (рис. 5б). В ядре циклона (слой 200–300 м) аномалии частоты ВБ относительно фоновой положительны (рис. 5в). Однако следует отметить, что в ядре циклона наблюдаются как положительные, так и отрицательные аномалии, но преобладают положительные.
Рис. 5.
Профили квадрата частоты ВБ, с–2: (a) фоновая $N_{0}^{2}(z)$; (б) ${{N}^{2}}(z)$ в центре вихря; (в) аномалии ${{N}^{2}}(z) - N_{0}^{2}(z)$ в центре вихря. Оранжевая и синяя линии относятся к циклону и антициклону соответственно.

В ядре антициклона (рис. 5б) вертикальные изменения частоты ВБ практически отсутствуют, так как ядро по плотности практически однородно (см. также рис. 4д), а аномалии частоты ВБ относительно фоновой частоты отрицательны (рис. 5в). Если рассматривать тонкие детали частоты ВБ в ядре антициклона, то следует отметить двухслойность ядра, состоящего из двух практически однородных по плотности слоев, в каждом из которых относительные колебания частоты ВБ весьма малы: $\left| {\frac{{{{N}^{2}}\left( {x,y,z,t} \right)}}{{N_{0}^{2}\left( z \right)}}} \right| < 0.01$. В районе горизонта 350 м это неравенство нарушается: $\frac{{{{N}^{2}}\left( {x,y,z,t} \right)}}{{N_{0}^{2}\left( z \right)}} \approx 0.05$, что указывает на слабый скачок плотности на этом горизонте. Однако среднее значение относительных колебаний частоты ВБ остается в том же диапазоне: $\left| {\frac{{{{N}^{2}}\left( {x,y,z,t} \right)}}{{N_{0}^{2}\left( z \right)}}} \right| < 0.01$.
Таким образом, в ядре циклона частота ВБ в среднем увеличивается, а в ядре антициклона уменьшается практически до полной однородности по плотности.
7. ПАРАМЕТР ВЕРТИКАЛЬНОЙ СПЛЮСНУТОСТИ ВИХРЕВЫХ ЯДЕР В СООТВЕТСТВИИ С ТЕОРИЕЙ ЭЛЛИПСОИДАЛЬНЫХ ВИХРЕЙ
На рис. 6, согласно соотношениям (23) из работы [26], приведена зависимость безразмерного ротора скорости $\frac{{{\text{ro}}{{{\text{t}}}_{z}}\vec {u}}}{\sigma }$ от параметра $K$ – это расстояние по вертикали от оси $K$ до линии $\frac{{{\text{ro}}{{{\text{t}}}_{z}}\vec {u}}}{\sigma }$ для осесимметричных вихрей. На этом же рисунке безразмерное значение $\frac{1}{\sigma }\frac{{{{\partial }^{2}}\psi }}{{\partial {{{\tilde {z}}}^{2}}}}$ – это расстояние по вертикали от линии $\frac{{{\text{ro}}{{{\text{t}}}_{z}}\vec {u}}}{\sigma }$ до единицы. В принятых ранее обозначениях $\frac{1}{\sigma }\frac{{{{\partial }^{2}}\psi }}{{\partial {{{\tilde {z}}}^{2}}}} = \varepsilon $, а $\frac{{{\text{ro}}{{{\text{t}}}_{z}}\vec {u}}}{\sigma } = 1 - \varepsilon $. Как видим, в сумме обе величины $\frac{{{\text{ro}}{{{\text{t}}}_{z}}\vec {u}}}{\sigma }$ и $\frac{1}{\sigma }\frac{{{{\partial }^{2}}\psi }}{{\partial {{{\tilde {z}}}^{2}}}}$ составляют единицу. Для малых значений $0 < K < 0.6$ преобладает слагаемое $\frac{1}{\sigma }\frac{{{{\partial }^{2}}\psi }}{{\partial {{{\tilde {z}}}^{2}}}}$, а для больших $K > 0.6$ большее значение имеет слагаемое $\frac{{{\text{ro}}{{{\text{t}}}_{z}}\vec {u}}}{\sigma }$; очевидно, они одинаковы при $K \cong 0.6$. Согласно графику на рис. 6, слагаемое $\frac{1}{\sigma }\frac{{{{\partial }^{2}}\psi }}{{\partial {{{\tilde {z}}}^{2}}}}$ значительно превышает $\frac{{{\text{ro}}{{{\text{t}}}_{z}}\vec {u}}}{\sigma }$ в тонких вихрях, т.е. в вихрях с малыми значениями параметра $K$. Это означает, что в тонких вихрях должна наблюдаться значительная перестройка поля плотности. Тем не менее, на толщину антициклонов накладывается ограничение $\varepsilon < \frac{1}{{1 + {\text{Ro}}}}$. В нашем случае ${\text{Ro}} = 0.3~$, поэтому и для параметра $\varepsilon $ это условие дает численное значение $\varepsilon < 0.77$, которое по приведенному графику можно пересчитать на параметр $K$, и для него получить свое ограничение $K > 0.18$, означающее, что антициклон не может быть слишком тонким. В общем случае предельное значение параметра ${{K}_{0}}$, привязанное к предельному значению ${{\varepsilon }_{0}} = \frac{1}{{1 + {\text{Ro}}}}$, зависит от числа Россби ${{K}_{0}} = {{K}_{0}}\left( {{\text{Ro}}} \right)$ и может трактоваться как ограничение на толщину ядра антициклона $\frac{{{{N}_{0}}}}{f}\frac{c}{{\sqrt {ab} }} > {{K}_{0}}$. При достижении предельных значений $\varepsilon = {{\varepsilon }_{0}}$ (или $K = {{K}_{0}}$) ядро антициклона становится полностью однородным по распределению плотности по вертикали. Условие $\frac{{{{N}_{0}}}}{f}\frac{c}{{\sqrt {ab} }} > {{K}_{0}}$ равносильно условию устойчивости стратификации в ядре вихря при конкретном числе Россби ${\text{Ro}}$. Аналогичных ограничений на циклон нет.
Рис. 6.
Зависимость безразмерного параметра $\frac{{{\text{ro}}{{{\text{t}}}_{z}}\vec {u}}}{\sigma }$ от параметра вертикальной сплюснутости $K$ для осесимметричных вихрей. При $K = 0$ $\frac{{{\text{ro}}{{{\text{t}}}_{z}}\vec {u}}}{\sigma } = 0$, при $K \to \infty $ $\frac{{{\text{ro}}{{{\text{t}}}_{z}}\vec {u}}}{\sigma } \to 1$.

Для вихрей, месторасположение которых п-оказано на рис. 2, рассчитан параметр сплюснутости их ядер [26]. Для циклона средняя частота ВБ ${{N}_{0}} = 2.59 \times {{10}^{{ - 3}}}\,\,{{{\text{с}}}^{{ - 1}}}$, для антициклона ${{N}_{0}} = 2.06 \times {{10}^{{ - 3}}}\,\,{{{\text{с}}}^{{ - 1}}}$ (рис. 5). Соответственно, параметры вертикальной сплюснутости для циклона $K = 0.13$, а для антициклона $K = 0.15$. Оба значения $K$ соответствуют тонким вихрям по нашей классификации. Отметим, что ограничение, полученное ранее на параметр $K > {{K}_{0}} = 0.18$ для антициклона хотя и не выполнено, но с небольшой погрешностью. Это может быть связано с тем, что ограничение $K > {{K}_{0}}$ получено в предположении осесимметричности вихря, т.е. параметра горизонтальной вытянутости ядра $\nu = 2$. В нашем случае вихрь асимметричен, и для антициклона этот параметр слегка больше $\nu = 2.2$. Согласно (5), асимметричность приводит к уменьшению значения ${{K}_{0}}$, что приблизит ${{K}_{0}}$ к $0.15$. Однако главная причина отличия оценки $K$ кроется в том, что верхняя граница ядра вихря находится очень близко к поверхности или даже соприкасается с ней. Ниже будет предложена корректировка значений $K$ с учетом близости ядра к поверхности моря.
8. ПРИМЕНЕНИЕ МЕТОДА ИЗОБРАЖЕНИЙ К АНАЛИЗИРУЕМЫМ ВИХРЯМ
Применив метод изображений к анализируемым вихрям, можно сделать вывод, что наличие поверхности моря должно привести к фактическому увеличению параметра $K$, но не более чем в два раза. В результате получим диапазон эффективного значения параметра вертикальной сплюснутости для циклона: $0.13 < K < 0.26$, аналогично для антициклона: $0.15 < K < 0.30$. Если фактическое значение $K$ будет близко к левому пределу неравенств, то влиянием поверхности моря можно пренебречь. Если же к правому, то влияние поверхности моря на перестройку поля плотности в ядрах вихрей будет очень важным.
Физически метод отображений используется в качестве замены приближения “твердой крышки” на поверхности моря, согласно которому на поверхности моря отсутствуют вертикальные движения. В реальности же поверхность моря деформируется движением вод, и это, в частности, можно зафиксировать на альтиметрических картах. В методе отображений не учитывается искривление свободной поверхности над подповерхностным вихрем, и это приводит к баротропному отклику по всей глубине моря. На горизонтах ниже ядра вихрей мы действительно наблюдаем “столб” завихренности, не затухающий при удалении вниз от вихревого ядра. Эффект “столба завихренности” может уменьшиться или вообще погаситься, если под поверхностью моря по каким-то причинам образуется прогиб изопикн противоположного направления, чем на поверхности моря. Этот эффект на сегодняшний день для нашего полигона практически не исследован и еще требует описания в модельных и натурных исследованиях.
9. ОПРЕДЕЛЕНИЕ ПО ЭКСПЕРИМЕНТАЛЬНЫМ ДАННЫМ КОЭФФИЦИЕНТА $\varepsilon $ КАК ВКЛАДА ЭФФЕКТА РАСТЯЖЕНИЯ В ПОТЕНЦИАЛЬНУЮ ЗАВИХРЕННОСТЬ ЯДРА. КОСВЕННОЕ ОПРЕДЕЛЕНИЕ ПАРАМЕТРА $K$
Будем исходить из рабочей формулы (10), полученной для постоянной фоновой частоты ВБ $N_{0}^{2}$. Тогда, зная ${{N}^{2}}$, $N_{0}^{2}$ и ${\text{Ro}}$, можно определить параметр $\varepsilon $. В реальности $N_{0}^{2}$ и ${{N}^{2}}$ зависят от координат профиля, а форма ядра отличается от эллипсоидальной. Предположим, что оценка ${\text{Ro}}$ справедлива по всему объему ядра, как и искомый параметр ${{\varepsilon }}$. Тогда получается, что фактически мы рассматриваем более сложную ситуацию, изложенную в разделе 2.4 первой части [26] (ядра со “сложной начинкой”). Из формулы (10) следует соотношение
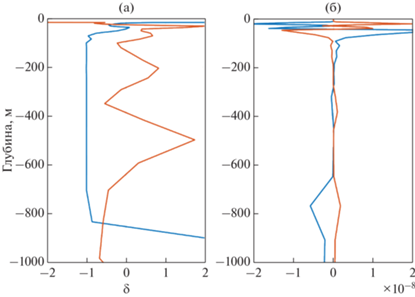
Рис. 7.
Послойно осредненные характеристики $\left\langle {{{N}^{2}} - N_{0}^{2}} \right\rangle $ (a) и $\delta = \frac{{\left\langle {{{N}^{2}} - N_{0}^{2}} \right\rangle }}{{\left\langle {N_{0}^{2}} \right\rangle }}$ (б) для циклона (оранжевые линии) и антициклона (синие линии).
Согласно рис. 7б, параметр $\delta \left( z \right)$ для горизонтов осреднения от 50 м до 833 м для антициклона равен $\delta = - 0.69 \approx - 0.7$. К сожалению, в этом подходе мы наблюдаем сильную зависимость параметра $\delta $ от глубины залегания верхней границы слоя. Так, если рассмотреть слой осреднения от 100 м до 833 м, то этот же параметр увеличится по абсолютной величине до $\delta \approx - 0.9$. Качественно это означает следующее: относительное изменение квадрата частоты ВБ в ядре антициклона весьма велико. Жидкость в ядре антициклона становится более однородной по плотности. Отметим, что последние оценки для квадрата частоты ВБ получены с использованием натурных данных в предположении постоянства фоновой частоты ВБ и справедливости теории эллипсоидальных вихрей. В реальности же эта теория может оказаться очень грубой для случая переменной фоновой частоты ВБ. Для количественной оценки в этом случае воспользуемся следствием из равенства (11) в пренебрежении вторым слагаемым, которое является малой величиной согласно рис. 7. Тогда
(14)
$\frac{1}{f}\frac{\partial }{{\partial z}}\frac{{{{f}^{2}}}}{{N_{0}^{2}\left( z \right)}}\frac{{\partial \psi \left( {x,y,z,t} \right)}}{{\partial z}} \approx \frac{{{{N}^{2}}\left( {x,y,z,t} \right) - N_{0}^{2}\left( z \right)}}{{N_{0}^{2}\left( z \right)}}.$На глубинах от 50 до 100 м параметр $\frac{{{{N}^{2}}\left( {x,y,z,t} \right) - N_{0}^{2}\left( z \right)}}{{N_{0}^{2}\left( z \right)}}$ для антициклона становится отрицательным и достигает значения $ - 1$ на горизонте 100 м. Ниже этой глубины и до горизонта 830 м параметр $\frac{{{{N}^{2}}\left( {x,y,z,t} \right) - N_{0}^{2}\left( z \right)}}{{N_{0}^{2}\left( z \right)}}$ остается с точностью не ниже 1% очень близким к $ - 1$ значением, что означает практически полную однородность плотности в вихревом ядре, исключая тонкий слой на глубине 350 м, где наблюдается слабый выброс в частоте ВБ или, что то же самое, слабый скачок в вертикальном распределении поля плотности. Интерпретация этого – следующая: ядро антициклона состоит из двух слоев однородной по плотности жидкости со слабо отличающимися значениями плотности в каждом слое. Поскольку перепад плотности незначительный, то, приближенно, ядро антициклона можно считать полностью однородным по плотности.
Итак, ядро антициклона практически однородно по плотности с численной оценкой осредненного квадрата частоты ВБ ядра $\left\langle {\frac{{{{N}^{2}}\left( {x,y,z,t} \right)}}{{N_{0}^{2}\left( z \right)}}} \right\rangle < $ $ < \,\,0.01$. Неравенство $\frac{{{{N}^{2}}\left( {x,y,z,t} \right)}}{{N_{0}^{2}\left( z \right)}} < 0.01$ выполняется локально на всех горизонтах вихревого ядра антициклона, кроме небольшого слоя в районе глубины 350 м. В качестве оценки квадрата частоты ВБ ядра антициклона примем
(15)
$\left\langle {{{N}^{2}}\left( {x,y,z,t} \right)} \right\rangle \approx 0.01\left\langle {N_{0}^{2}\left( z \right)} \right\rangle .$(16)
$\left\langle {{{N}^{2}}\left( {x,y,z,t} \right)} \right\rangle \approx 1.4\left\langle {N_{0}^{2}\left( z \right)} \right\rangle .$Рис. 8.
$\frac{{{{N}^{2}}\left( {x,y,z,t} \right) - N_{0}^{2}\left( z \right)}}{{N_{0}^{2}\left( z \right)}}$ (а) и $\frac{g}{{{{\rho }_{*}}}}\left( {\rho \left( {x,y,z,t} \right) - {{\rho }_{0}}\left( z \right)} \right)\frac{\partial }{{\partial z}}\left\{ {\frac{1}{{N_{0}^{2}\left( z \right)}}} \right\}$ (б) как функции глубины z для циклона (оранжевый цвет) и антициклона (синий цвет).
Итак, мы использовали два подхода к оценке вклада эффекта растяжения в потенциальную завихренность жидких частиц (фактически оценке второго слагаемого в соотношении (1)). В первом, более грубом, подходе для получения оценки используется постоянная фоновая частота ВБ, а затем, считая частоту переменной, мы усредняли результат по толщине ядра. При таком подходе активно использовалась аналитическая теория эллипсоидальных вихрей. Во втором подходе на частоту ВБ не накладывалось никаких ограничений и второе слагаемое вычислялось напрямую из натурных данных. Второй подход более физичен, но в нем нет возможности обоснованного использования аналитических результатов, поскольку для общего случая соответствующая теория не построена. Как показали расчеты, оба подхода дают качественно одинаковые результаты. Однако для количественной оценки значимости эффекта растяжения в потенциальной завихренности жидких частиц вихревых ядер следует пользоваться более точным подходом (13).
По величине $\delta = 0.5$ и числу Россби ${\text{Ro}} = 0.3$ из равенства $\varepsilon = \frac{\delta }{{{\text{Ro}} + \delta }}$ можно оценить вклад эффекта растяжения в потенциальную завихренность циклона $\varepsilon = 0.63$. Соответственно, вращение дает остальные 37%. Как видим, роль обоих эффектов значительна, но эффект растяжения все-таки более важен.
Для косвенной оценки параметра вертикальной сплюснутости $K$ ядра циклона воспользуемся графиком зависимости $\frac{1}{\sigma }{\text{ro}}{{{\text{t}}}_{z}}\vec {u}~$ от $K$ (рис. 6). Значению $\frac{1}{\sigma }{\text{ro}}{{{\text{t}}}_{z}}\vec {u} = 0.37$ соответствует значение $K = 0.26$, назовем его эффективным параметром вертикальной сплюснутости. Сравнивая его с диапазоном $0.13 < K < 0.26$, полученным ранее прямым расчетом и поправкой на наличие свободной поверхности моря, делаем вывод, что поверхность моря сильно повлияла на перестройку поля плотности в ядре циклона, поскольку эффективное значение параметра $K = 0.26$ совпадает с правой границей диапазона.
Аналогичная работа по натурным данным для антициклона показывает, что в антициклоне относительному изменению частоты ВБ $\delta = - 0.7~$ и ${\text{Ro}} = 0.3$ соответствует значение $\varepsilon = 0.70$. Оценка эффективного параметра вертикальной сплюснутости для антициклона $K = 0.34$. Диапазон значений $K$ из теории эллипсоидальных вихрей с учетом влияния поверхности моря – $0.15 < K < 0.30$. Ограничения из условий устойчивости стратификации следующие: $\varepsilon < 0.77$ и $K > {{K}_{0}} = 0.18$, с округлением до десятых долей даст в результате ${{K}_{0}} = 0.2$.
Вся теория, на которую мы опирались, построена для процессов с малыми числами Россби ${\text{Ro}}$. В нашем случае ${\text{Ro}} = 0.3$. Это означает, что геострофическая компонента скоростей составляет 0.7 от общей скорости, а 30% – это агеострофические скорости, которые в теории отсутствуют, однако могут присутствовать в натурных данных. Разумно полагать, что точность теории по скоростям в целом также составляет примерно 30%. Поэтому все численные результаты по скоростям, отличающиеся менее чем на 30%, должны восприниматься как совпадающие. В этом смысле разумно полагать, что $K = 0.34$ и $K = 0.30$ – это практически одно и то же. Чтобы убрать это несоответствие, округлим указанные числа до десятых долей. В результате для циклона и антициклона параметры вертикальной сплюснутости окажутся совпадающими: $K = 0.3$. При этом ограничение на $K$ для антициклона выполняется, поскольку ${{K}_{0}} = 0.2$.
10. ЗАКЛЮЧЕНИЕ И ВЫВОДЫ
В работе исследуется роль частоты ВБ в мезомасштабных вихрях. В качестве примера по данным океанического реанализа GLORYS12V1 рассматриваются два вихря Лофотенской котловины Норвежского моря: циклон и антициклон. Для этих вихрей построены вертикальные разрезы потенциальной плотности и частоты ВБ, рассчитаны масштабы и орбитальные скорости, построены распределения частоты ВБ в ядре и ее аномалии относительно фоновой частоты ВБ, а также графики относительной и потенциальной завихренности. Анализ этих результатов позволил получить следующие выводы:
• Орбитальные скорости в циклоне достигают 30 см/с, а пространственные продольный и поперечный масштабы составляют 72.3 и 48.8 км соответственно.
• Орбитальные скорости в антициклоне превышают 50 см/с (максимальное значение – 50.8 см/с), а пространственные продольный и поперечный масштабы – 108.7 и 67.9 км.
• Изопикны в циклонах и антициклонах деформируются в среднем в противоположных направлениях. Циклонические вихри сближают изопикны, втягивая ближние внешние изопикны внутрь вихревого ядра, в то же время антициклонические вихри раздвигают изопикны друг от друга. Последнее приводит к увеличению частоты ВБ в вихревом ядре циклона и соответствующему ее уменьшению в антициклоне. Показано, что аномалии частоты ВБ относительно фоновой частоты положительны в ядре циклона и отрицательны в ядре антициклона. Относительные изменения квадрата частоты ВБ оказались значительными: для циклона – порядка 50%, а для антициклона – 99%. Теоретическое обоснование этого факта описывается формулой (10) первой части работы [26]. На рис. 5в дано подтверждение на соответствующих графиках.
• Эффективная перестройка частоты ВБ происходит исключительно в тонких вихрях с малыми параметрами вертикальной сплюснутости ядра $K$. Для антициклонов существует ограничение снизу на число $K > {{K}_{0}}$. Критическое ${{K}_{0}}$ связано безразмерными геометрическими параметрами ядра вихря и средним по вертикали значением квадрата частоты ВБ. Согласно теоретическим расчетам и оценкам по натурным данным, для выбранных вихрей – как циклона, так и антициклона – получены совпадающие значения указанных параметров $K = 0.3$, при этом ${{K}_{0}} = 0.2$.
• Потенциальная завихренность, рассчитываемая по формуле (1), как и относительная завихренность, хорошо выделяются в вихревых ядрах и прослеживаются в вихрях до самого дна (как в циклоне, так и в антициклоне).
• Расположение вихревых ядер вблизи поверхности моря приводит к тому, что поверхность моря оказывает значительное влияние на динамику вихрей, что, в свою очередь, отражается в увеличении эффективного значения параметра вертикальной сплюснутости вихревых ядер, оценочно – вдвое.
Благодарности. Авторы благодарят членов ученого совета Института океанологии, участвовавших в обсуждении данной работы.
Источники финансирования. Работа выполнена при финансовой поддержке гранта РНФ № 22-27-00004 и по теме государственного задания 0128-2021-0002.
The publication was funded by the Russian Science Foundation, project N 22-27-00004 and in the framework of the Shirshov Institute of Oceanology RAS state assignment N 0128-2021-0002.
Список литературы
Белоненко Т.В., Волков Д.Л., Норден Ю.Е., Ожигин В.К. Циркуляция вод в Лофотенской котловине Норвежского моря // Вестник СПбГУ. 2014. Т. 7. № 2. С. 108–121.
Белоненко Т.В., Колдунов А.В., Сентябов Е.В., Карсаков А.Л. Термохалинная структура Лофотенского вихря Норвежского моря на основе экспедиционных исследований и по данным гидродинамического моделирования // Вестник Санкт-Петербургского университета. Науки о Земле. 2018. Т. 63. № 4. С. 502–519. https://doi.org/10.21638/spbu07.2018.406
Жмур В.В. Мезомасштабные вихри океана. Москва: ГЕОС, 2011. 384 с.
Жмур В.В., Новоселова Е.В., Белоненко Т.В. Потенциальная завихренность в океане: подходы Эртеля и Россби с оценками для Лофотенского вихря // Известия РАН. Физика атмосферы и океана. 2021. Т. 57. № 6. С. 721–732. https://doi.org/10.31857/S0002351521050151
Жмур В.В., Панкратов К.К. Динамика эллипсоидального приповерхностного вихря в неоднородном потоке // Океанология. 1989. Т. 29. № 2. С. 205–211.
Жмур В.В., Щепеткин А.Ф. Эволюция эллипсоидального вихря в стратифицированном океане в приближении f-плоскости // Известия АН СССР. Физика атмосферы и океана. 1991. Т. 27. № 5. С. 492–503.
Колдунов А.В., Белоненко Т.В. Гидродинамическое моделирование поля вертикальной скорости в Лофотенском вихре // Известия РАН. Физика атмосферы и океана. 2020. Т. 56. № 5. С. 575–585. https://doi.org/10.31857/S0002351520040045
Наумов Л.М., Гордеева С.М. Боковой перенос тепла и соли в Лофотенском бассейне: сравнение на основе трех баз данных // Фундаментальная и прикладная гидрофизика. 2020. Т. 13. № 3. С. 43–55. https://doi.org/10.7868/S207366732003003X
Новоселова Е.В., Белоненко Т.В. Изопикническая адвекция в Лофотенской котловине Норвежского моря // Фундаментальная и прикладная гидрофизика. 2020. Т. 13. № 3. С. 56–67. https://doi.org/10.7868/S2073667320030041
Травкин В.С., Белоненко Т.В. Оценка глубины зимней конвекции в Лофотенской котловине Норвежского моря и методы ее оценки // Гидрология и экология (Ученые записки РГГМУ). 2020. Т. 59. С. 67–83. https://doi.org/10.33933/2074-2762-2020-59-67-83
Федоров А., Башмачников И., Белоненко Т. Зимняя конвекция в Лофотенской котловине по данным буев ARGO и гидродинамического моделирования // Вестник Санкт-Петербургского университета. Науки о Земле. 2019. Т. 64. № 3. С. 491–511. https://doi.org/10.21638/spbu07.2019.308
Bashmachnikov I., Belonenko T., Kuibin P. et al. Pattern of vertical velocity in the Lofoten vortex (the Norwegian Sea) // Ocean Dynamics. 2018. V. 68. № 12. P. 1711–1725. https://doi.org/10.1007/s10236-018-1213-1
Belonenko T.V., Travkin V.S., Koldunov A.V., Volkov D.L. Topographic experiments over dynamical processes in the Norwegian Sea // Russ. J. Earth. Sci. 2021. V. 21. ES1006. https://doi.org/10.2205/2020ES000747
Belonenko T.V., Zinchenko V.A., Fedorov A.M. et al. Interaction of the Lofoten vortex with a satellite cyclone // Pure and Applied Geophysics. 2021. V. 178. P. 287–300. https://doi.org/10.1007/s00024-020-02647-1
Belonenko T., Zinchenko V., Gordeeva S., Raj R.P. Evaluation of heat and salt transports by mesoscale eddies in the Lofoten Basin // Russ. J. Earth Sci. 2020. V. 20. ES6011. https://doi.org/10.2205/2020ES000720
Fedorov A.M., Belonenko T.V. Interaction of mesoscale vortices in the Lofoten Basin based on the GLORYS database // Russian Journal of Earth Sciences. 2020. V. 20. № 2. ES2002. https://doi.org/10.2205/2020ES000694
Gordeeva S., Zinchenko V., Koldunov A. et al. Statistical analysis of long-lived mesoscale eddies in the Lofoten Basin from satellite altimetry // Advances in Space Research. 2020. https://doi.org/10.1016/j.asr.2020.05.043
IOC, SCOR and IAPSO. The international thermodynamic equation of seawater – 2010: Calculation and use of thermodynamic properties. Intergovernmental Oceanographic Commission, Manuals and Guides No. 56, UNESCO (English), 2010. 196 p.
Kennelly M.A., Evens R.H., Joyce T.M. Small-scale cyclones on the periphery of Gulf Stream warm-core rings // J. Geophys. Res. 1985. V. 90. № C5. P. 8845–8857.
Meacham S.P., Pankratov K.K., Shchepetkin A.F., Zhmur V.V. The interaction of ellipsoidal vortices with background shear flows in a stratified fluid // Dynamics of Atmospheres and Oceans. 1994. V. 21. № 2–3. P. 167–212. https://doi.org/10.1016/0377-0265(94)90008-6
Pankratov K.K., Zhmur V.V. Dynamics of desinglarized quasigeostrophic vortices // Physics of Fluids A: Fluid Dynamics. 1991. V. 3 (5). P. 1464–1464. https://doi.org/10.1063/1.857998
Raj R.P., Halo I., Chatterjee S. et al. Interaction between mesoscale eddies and the gyre circulation in the Lofoten Basin // Journal of Geophysical Research: Oceans. 2020. V. 125. № 7. e2020JC016102. https://doi.org/10.1029/2020JC016102
Sandalyuk N.V., Bosse A., Belonenko T.V. The 3D structure of Mesoscale Eddies in the Lofoten Basin of the Norwegian Sea: A composite analysis from altimetry and in situ data // Journal of Geophysical Research: Oceans. 2020. V. 125. e2020JC016331. https://doi.org/10.1029/2020JC016331
Travkin V.S., Belonenko T.V. Seasonal variability of mesoscale eddies of the Lofoten Basin using satellite and model data // Russian Journal of Earth Sciences. 2019. V. 19. № 5. ES5004. https://doi.org/10.2205/2019ES000676
Volkov D.L., Belonenko T.V., Foux V.R. Puzzling over the dynamics of the Lofoten Basin – a sub-Arctic hot spot of ocean variability // Geophys. Res. Lett. 2013. V. 40. № 4. P. 738–743. https://doi.org/10.1002/grl.50126
Zhmur V.V., Novoselova E.V., Belonenko T.V. Peculiarities of formation of the density field in mesoscale eddies of the Lofoten Basin: Part 1 // Oceanology. 2021. V. 61. № 6. P. 830–838. https://doi.org/10.1134/S0001437021060333
Zinchenko V.A., Gordeeva S.M., Sobko Yu.V., Belonenko T.V. Analysis of mesoscale eddies in the Lofoten Basin based on satellite altimetry // Fundamentalnaya i Prikladnaya Gidrofzika. 2019. V. 12. № 3. P. 46–54. https://doi.org/10.7868/S2073667319030067
Дополнительные материалы отсутствуют.
Инструменты
Океанология



