Океанология, 2022, T. 62, № 5, стр. 705-714
Законы движения водоплавающих и их использование при движении подводных объектов
Н. Н. Корчагин 1, 2, *, Н. И. Сидняев 2, А. А. Федотов 2
1 Институт океанологии им. П.П. Ширшова РАН
Москва, Россия
2 Московский государственный технический университет им. Н.Э. Баумана
Москва, Россия
* E-mail: e-niknik@mail.ru
Поступила в редакцию 10.01.2022
После доработки 11.03.2022
Принята к публикации 14.04.2022
- EDN: YLTDIB
- DOI: 10.31857/S0030157422050082
Аннотация
В рамках идеальной несжимаемой жидкости рассмотрено обтекание тонкого крыла конечного размаха, моделирующего работу хвостового плавника дельфина. Исследовано движение дельфина, совершающего хвостовым плавником перпендикулярные направлению основного движения периодические колебания при практически равномерном и прямолинейном движении центра масс. Изучено обтекание колеблющегося крыла, работающего в режиме создания силы тяги и с образованием завихренного следа за крылом. Параметры модели подобраны по данным экспериментальных наблюдений. Получено численное решение задачи с расчетами кинематических и силовых характеристик модели хвостового плавника дельфина.
ВВЕДЕНИЕ
Интерес к изучению обтекания движущихся в морской среде животных (прежде всего, дельфинов и китообразных), а также к биомеханике связан с развитием судостроения: как надводных кораблей, так и подводных технических конструкций. Не менее важно к этому отнести и усовершенствование самодвижущихся подводных объектов (СПО). В этой связи исследователи с особым интересом подходят к проблеме создания новых видов транспортных средств, принципы работы которых основаны на применении выработанных природой у водоплавающих методов и средств в ускоренном передвижении в морской среде с минимально возможными усилиями. При этом длительная биологическая эволюция, направляемая и стимулируемая борьбой за существование, привела к развитию у животных наиболее рациональных способов плавания и полета. Поэтому изучение механизмов образования силы тяги и подъемной силы у биоособей в живой природе может служить одним из подходов к решению задач по усовершенствованию движения современных транспортных средств с учетом действия механизма с аналогами работы, например, хвостового плавника дельфина (и иных биоособей) или колеблющегося крыла у птиц, действующих в качестве рабочих элементов [1, 5, 7, 13, 14].
В проведенных исследованиях параметры биомоделей выбраны в соответствии с данными наблюдений [2, 3, 5, 8]. В результате на основе обработки экспериментальных данных по составленным ранее авторами специальным программам и проведения соответствующих численных расчетов были получены новые сведения в области биогидродинамики с возможностью использования их в задачах усовершенствования динамических характеристик обтекаемых под водой объектов. Эти исследования могут быть использованы при создании средств в освещение подводной обстановки в прибрежных морях России.
ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ О ПЛАВАНИИ ДЕЛЬФИНОВ
Известно, что движения крупных быстро плавающих животных, например, дельфинов, характеризуются большими числами Рейнольдса ${\text{Re}} = {{VL} \mathord{\left/ {\vphantom {{VL} \nu }} \right. \kern-0em} \nu } \gg 1$ [16] ($V$ – средняя скорость движения, $L$ – длина животного, $\nu $ – кинематический коэффициент вязкости воды). Значение ${\text{Re}}$ для различных рыб и китообразных при нормальных условиях плавания изменяется в пределах ${{10}^{4}} < {\text{Re}} < {{10}^{8}}$. В экспериментах по определению кинематических характеристик плавания дельфинов число ${\text{Re}}$ изменялось от $3 \times {{10}^{6}}$ до $1.4 \times {{10}^{7}}$ [3].
Дельфины имеют хорошо обтекаемую форму и обтекаются без отрыва потока от тела. В [11] эксперименты показали, что до хвостового плавника (при значениях ${x \mathord{\left/ {\vphantom {x L}} \right. \kern-0em} L} < 0.89$, здесь $0 \leqslant x \leqslant L$, $x$ – расстояние от передней точки носа модели до фиксированного сечения) режим обтекания дельфина является безотрывным. В то же время на жесткой модели дельфина на всей ее задней половине (при ${x \mathord{\left/ {\vphantom {x L}} \right. \kern-0em} L} \geqslant 0.55$) осуществляется отрывной режим обтекания. О безотрывном обтекании дельфина свидетельствуют и прямые наблюдения за дельфинами, плавающими в условиях биолюминесценции (свечения) моря. Зафиксированы случаи, когда исследователи наблюдали, как ночью при тихой погоде в море за стремительно плывущим дельфином остаются лишь два светящихся шнура, а за плывущим тюленем – широкая светящаяся область. Известно, что дельфин плывет, почти не нарушая спокойного состояния воды [12]. Пограничный слой, примыкающий к поверхности его тела, тонкий. Наибольшая толщина пограничного слоя (в конце у хвоста) обычно составляет не больше чем несколько процентов толщины животного [16]. Дельфины имеют форму вытянутого тела и сильное сужение перед хвостовым плавником (например, диаметр тела дельфина афалины относится к его длине примерно как 1 : 6 [4]). Таким образом, хвостовой плавник дельфина практически движется в невозмущенном потоке и влиянием корпуса дельфина на работу его хвостового плавника можно пренебречь [4].
КИНЕМАТИЧЕСКАЯ И СИЛОВАЯ МОДЕЛИ ХВОСТОВОГО ПЛАВНИКА ДЕЛЬФИНА
Для создания необходимой силы тяги дельфин совершает хвостовым плавником перпендикулярные направлению основного движения колебания с амплитудами порядка поперечных размеров всего тела. В этом случае обтекание хвостового плавника дельфина можно формулировать как задачу о нестационарном обтекании потоком несжимаемой жидкости крыла конечного размаха, совершающего колебания с большой амплитудой.
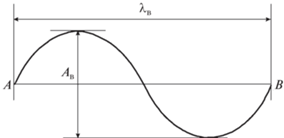
Результаты исследования кинематических характеристик плавания дельфинов в натурных условиях, морском бассейне, биогидродинамическом канале [1–3, 8, 10] показывают, что при длительном неизменном режиме плавания все точки тела дельфина описывают волнообразные траектории наименьшего размаха для близких к центру точек масс тела и наибольшего – для точек хвостового плавника. Амплитуда колебаний центра масс животного составляет при этом всего несколько процентов от амплитуды колебаний точки развилки хвостового плавника. Практически можно считать, что центр масс движется прямолинейно. В этом случае траектория точки развилки хвостового плавника анализировалась по последовательным или выборочным циклам колебаний (рис. 1). В результате поступательное перемещение дельфина в данном цикле соответствовало положению замыкающей линии $AB$, проведенной из начальной точки $A$ в конечную точку $B$ траектории этого цикла. Длина отрезка $AB$ обозначена как длина волны ${{\lambda }_{{\text{в}}}}$, размах волны – ${{A}_{{\text{в}}}}$.
Ниже на рис. 2 приведены результаты проводившихся в биогидродинамическом канале квадратного поперечного сечения $4\,{{{\text{м}}}^{2}}$ экспериментальных исследований по определению кинематических характеристик плавания дельфина афалины [2]. Регистрация элементов хвостового плавника дельфина осуществлялась с помощью киносъемки. Для последующей обработки отбирались кинокадры тех опытов, в которых траектория движения центра масс дельфина была почти прямолинейна и близка к горизонтальной осевой линии канала, а хвостовой плавник не совершал вращательных движений вокруг корневой хорды. Т.е. в этих опытах плавник проектировался на вертикальную плоскость (боковую стенку канала) только корневым профилем, который заменяли его корневой хордой.
Рис. 2.
Зависимости кинематических характеристик плавания дельфина афалины: 2а – положения корневой хорды AB плавника в последовательные моменты времени $t$; 2б, 2в – скорости точки хвостового плавника (точка $O{\kern 1pt} '$); 2г, 2д – зависимости углов $\gamma ,\,\,\beta $ и $\alpha $ от времени; 2е – положение корневой хорды в системе координат ${{y}^{1}},{{y}^{2}},{{y}^{3}}$; $h$ – амплитуда вертикальных колебаний, ${{{\mathbf{V}}}_{*}}$ – скорость точки $O{\kern 1pt} '$, $n$ – номера кинокадров.

На рис. 2а на плоскости $xOy$ изображены положения корневой хорды плавника в последовательные моменты времени. Вдоль оси $x$ отложены время $t$ в секундах и соответствующие положениям корневой хорды плавника номера кинокадров $n$. Зависимости от времени горизонтальной ${{V}_{0}}$ и вертикальной ${{V}_{y}}$ составляющих скорости (в м/с) некоторой точки хвостового плавника показаны на рис. 2б и 2в. Эту точку будем считать заданной на корневой хорде плавника (в центре точка Ó). На рис. 2 показаны зависимости углов $\gamma ,\,\,\beta $ и $\alpha $ от времени. Угол $\gamma $ определяется как угол наклона вектора скорости данной точки к направлению поступательного движения дельфина – к оси $x$, $\beta $ – мгновенный угол наклона корневой хорды к оси $x$, $\alpha = \gamma - \beta $ – угол атаки, угол между вектором скорости рассматриваемой точки и корневой хордой плавника. Причем максимум угла атаки $\alpha $, полученный из анализа траекторий точек хвостового плавника, как правило, не превышал $10^\circ $, а средние значения лежат в пределах ±($4^\circ {\kern 1pt} - {\kern 1pt} 6^\circ $).
Отметим, что, по аналогии с работой [15], пользуясь данными на рис. 2, схематически можно представить типичный для морских животных механизм создания силы тяги: хвостовой плавник движется так, что на каждом полупериоде колебаний возникает сила, действующая в направлении горизонтального движения животного. Подъемная сила за период при таком движении практически равна нулю11.
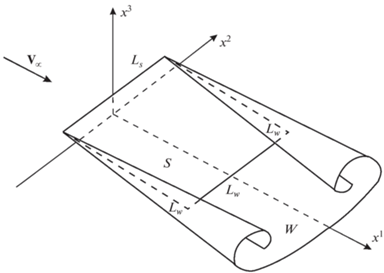
Далее, хвостовой плавник дельфина будем моделировать тонким плоским крылом. Полагаем, что крыло совершает периодические угловые колебания вокруг горизонтальной оси, фиксированной в плоскости крыла и параллельной прямолинейной задней кромке. В свою очередь ось угловых колебаний, расположенная поперек направления основного движения, совершает вертикальные гармонические колебания. Ниже на рис. 3 приведена схема обтекания крыла.
Здесь можно представить, что бесконечно тонким крылом уместно схематизировать реальное крыло, имеющее закругленную кромку ${{L}_{S}}$, обтекаемую без отрыва потока, и острую кромку ${{L}_{W}}$, с которой в поток жидкости плавно стекает вихревой след, возникающий за крылом при его движении. Можно считать, что крыло является несущей поверхностью $s$ с передней кромкой ${{a}^{1}} = 0,$ $ - 1 \leqslant {{a}^{2}} \leqslant 1,$ обтекаемой без отрыва, на которую действует подсасывающая сила [6, 15]. С задней ${{a}^{1}} = 1$, $ - 1 \leqslant {{a}^{2}} \leqslant 1$ и боковой $ - 1 \leqslant {{a}^{1}} \leqslant 1,$ ${{a}^{2}} = \pm 1$ кромок в поток стекает свободная вихревая поверхность $w$. Передняя кромка ${{a}^{1}} = 0,$ $ - 1 \leqslant {{a}^{2}} \leqslant 1$ – кромка натекания ${{L}_{S}}$, задняя ${{a}^{1}} = 1$, $ - 1 \leqslant {{a}^{2}} \leqslant 1$ и боковые кромки $0 \leqslant {{a}^{1}} \leqslant 1,$ ${{a}^{2}} = \pm 1$ – кромка стекания ${{L}_{W}}$; ${{a}^{1}},{{a}^{2}}$ – лагранжевы координаты точек несущей поверхности $s$.
Итак, в декартовой системе координат ${{x}^{1}},{{x}^{2}},{{x}^{3}}$ поток на бесконечности считаем однородным с постоянной скоростью ${{V}_{\infty }}$, параллельным оси ${{x}^{1}}$ и направленным в положительную сторону этой оси. Движение крыла опишем в системе координат ${{y}^{1}},{{y}^{2}},{{y}^{3}}$ (рис. 2е), в которой жидкость на бесконечности покоится и оси которой параллельны соответственно осям системы координат ${{x}^{{\text{1}}}}{\text{,}}{{x}^{{\text{2}}}}{\text{,}}{{x}^{{\text{3}}}}$. Ось угловых колебаний, параллельная оси ${{y}^{2}}$, движется вдоль вертикальной оси по закону ${{y}^{{\text{3}}}} = h{\text{cos(}}wt{\text{)}}$, а вдоль горизонтальной оси – по закону ${{y}^{1}} = - {{V}_{\infty }}t$. Крыло проектируется на плоскость ${{y}^{1}}{{y}^{3}}$ корневой хордой $AB$, ось угловых колебаний – точкой $O{\kern 1pt} '$ (см. рис. 2е). Таким образом, положение крыла в каждый момент времени определяется положением оси угловых колебаний и углом наклона хорды $AB$ к оси ${{y}^{1}}$ – углом $\beta $. Угол атаки крыла $\alpha $ определяется как угол между вектором мгновенной скорости оси вращения ${{{\mathbf{V}}}_{*}}$ и хордой крыла $AB$. Угол $\gamma $ – это угол между вектором ${{{\mathbf{V}}}_{*}}$ и осью ${{y}^{1}}$.
Хвостовой плавник дельфина представляет собой подводное с симметричным профилем гидродинамическое крыло сложной формы в плане. На рис. 4, в качестве примера, приведен профиль хвостового плавника дельфина из работы [9], в которой дано описание хвостовых плавников дельфинов и китов. Показано, что основным профилем хвостовых плавников китообразных является обобщенный симметричный профиль Жуковского НЕЖ-I с некоторыми изменениями в задней части.
Из рис. 4 видно, что форма крыла 1 в плане представляется относительно хорошим приближением к форме хвостового плавника дельфина. На основе вышеизложенного движение крыла 1 может описываться уравнениями (1):
(1)
$\begin{gathered} {{x}^{1}} = \left\{ {b\left[ {{{a}^{1}} + {{c}_{0}}(1 - {{a}^{1}}){{{({{a}^{2}})}}^{2}}} \right] - {{b}_{0}}} \right\} \times \\ \times \,\,\cos \beta (t) + {{b}_{0}}, \\ {{x}^{2}} = b\lambda \left( {1 - {{{{c}_{0}}} \mathord{\left/ {\vphantom {{{{c}_{0}}} 3}} \right. \kern-0em} 3}} \right){{{{a}^{2}}} \mathord{\left/ {\vphantom {{{{a}^{2}}} 2}} \right. \kern-0em} 2}, \\ {{x}^{3}} = \left\{ {b\left[ {{{a}^{1}} + {{c}_{0}}(1 - {{a}^{1}}){{{({{a}^{2}})}}^{2}}} \right] - {{b}_{0}}} \right\} \times \\ \times \,\,\sin \beta (t) + h\cos (\omega t), \\ 0 \leqslant {{a}^{1}} \leqslant 1,\,\,\,\, - {\kern 1pt} 1 \leqslant {{a}^{2}} \leqslant 1, \\ \beta (t) = \gamma (t) - \alpha (t), \\ \gamma (t) = \operatorname{arctg} \left( {\frac{{\omega h}}{{{{V}_{\infty }}}}\sin (\omega t)} \right), \\ \alpha (t) = {{\alpha }_{0}}\sin (\omega t). \\ \end{gathered} $Удлинение крыла $\lambda = {{4{{l}^{2}}} \mathord{\left/ {\vphantom {{4{{l}^{2}}} S}} \right. \kern-0em} S}$, где $l$ и $S$ – полуразмах крыла и его площадь соответственно, вычислялись по формуле $S = 2bl(1 - {{{{c}_{0}}} \mathord{\left/ {\vphantom {{{{c}_{0}}} 3}} \right. \kern-0em} 3})$. Тогда параметр ${{c}_{0}} = 3(1 - {{2l} \mathord{\left/ {\vphantom {{2l} {{{\lambda }}b}}} \right. \kern-0em} {{{\lambda }}b}})$.
Далее, уравнения движения крыла обезразмериваем и приводим к виду:
(2)
$\begin{gathered} {{x}^{1}} = \left[ {{{a}^{1}} + {{c}_{0}}(1 - {{a}^{1}}){{{({{a}^{2}})}}^{2}} - b_{0}^{{\text{'}}}} \right] \times \\ \times \,\,\cos \beta (t) + b_{0}^{{\text{'}}}, \\ {{x}^{2}} = \lambda \left( {1 - {{{{c}_{0}}} \mathord{\left/ {\vphantom {{{{c}_{0}}} 3}} \right. \kern-0em} 3}} \right){{{{a}^{2}}} \mathord{\left/ {\vphantom {{{{a}^{2}}} 2}} \right. \kern-0em} 2}, \\ {{x}^{3}} = \left[ {{{a}^{1}} + {{c}_{0}}(1 - {{a}^{1}}){{{({{a}^{2}})}}^{2}} - b_{0}^{{\text{'}}}} \right] \times \\ \times \,\,\sin \beta (t) + h{\kern 1pt} '\cos (\omega {\kern 1pt} {\text{'}}t), \\ 0 \leqslant {{a}^{1}} \leqslant 1,\,\,\,\, - {\kern 1pt} 1 \leqslant {{a}^{2}} \leqslant 1, \\ \beta (t) = \gamma (t) - \alpha (t), \\ \gamma (t) = \operatorname{arctg} \left( {\omega {\kern 1pt} {\text{'}}h{\kern 1pt} '\sin (\omega {\kern 1pt} {\text{'}}t)} \right), \\ \alpha (t) = {{\alpha }_{0}}\sin (\omega {\kern 1pt} {\text{'}}t). \\ \end{gathered} $Для безразмерных координат и безразмерного времени сохранены обозначения, соответствующие размерным величинам. При этом крыло считается жестким, поскольку у основной части плавника отсутствуют крупные деформации [5].
Значения кинематических параметров и их диапазоны изменения в представленной работе получены в результате обработки экспериментальных данных работ [3, 10]. Геометрические размеры и масса тел подопытных животных приведены в таблице 1 [4]. Вычисления амплитуды $h{\kern 1pt} '$ и частоты $\omega {\kern 1pt} {\text{'}}$ проводились по формулам $h{\kern 1pt} ' = {{{{A}_{0}}} \mathord{\left/ {\vphantom {{{{A}_{0}}} b}} \right. \kern-0em} b}$ и $\omega {\kern 1pt} {\text{'}} = {{2\pi fb} \mathord{\left/ {\vphantom {{2\pi fb} {{{V}_{0}}}}} \right. \kern-0em} {{{V}_{0}}}}$, где ${{A}_{0}}$ и $f$ – экспериментально наблюдаемые значения амплитуды и частоты колебаний точки развилки хвостового плавника; ${{V}_{0}}$ – скорость движения центра масс тела дельфина; длина корневой хорды плавника $b$ принята равной $0.1L$. Заметим, что отношение ${b \mathord{\left/ {\vphantom {b L}} \right. \kern-0em} L}$ у шести подопытных дельфинов (табл. 1) меняется от $0.085$ до $0.121$. Амплитуда изменения угла атаки ${{{{\alpha }}}_{0}}$ принята равной ${{10}^{^\circ }}$ (см. рис. 2д), а средний угол атаки $\bar {\alpha }$ на полупериоде колебания определялся по формуле
Таблица 1.
Геометрические и кинематические характеристики подопытных дельфинов
| Параметр/объект | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Длина $L$, м | 2.35 | 2.40 | 2.40 | 2.45 | 2.55 | 2.65 |
| Корневая хорда $b$, м | 0.21 | 0.22 | 0.29 | 0.23 | 0.22 | 0.225 |
| Размах хв. пл. ${{l}_{{{\text{хв}}{\text{.}}{\kern 1pt} {\kern 1pt} {\text{пл}}}}}$, м | 0.53 | 0.32 | 0.58 | 0.54 | 0.59 | 0.61 |
| Приведенный диаметр, м | 0.41 | 0.39 | 0.415 | 0.43 | 0.42 | 0.455 |
| Масса, кг | 150 | 140 | 160 | 185 | 175 | 210 |
| Удлинение хв. пл. $\lambda $ | 4.3 | 3.7 | 3.5 | 4.1 | 4.3 | 4.1 |
ОБТЕКАНИЕ МОДЕЛИ И ЭФФЕКТИВНОСТЬ РАБОТЫ ХВОСТОВОГО ПЛАВНИКА ДЕЛЬФИНА
Система уравнений с соответствующими начальными и граничными условиями, описывающая обтекание крыла с заданным законом движения (2), приведена в [7, 13, 14].
Численный метод решения представлен в [7].
По результатам численного решения определялись мгновенный ${{C}_{{{{T}_{i}}}}}$ и средний ${{C}_{T}}$ коэффициенты силы тяги и коэффициент полезного действия крыла $\eta $. Коэффициент ${{C}_{{{{T}_{i}}}}}$ определялся как отношение мгновенной силы тяги к значению ${{\rho V_{\infty }^{2}S} \mathord{\left/ {\vphantom {{\rho V_{\infty }^{2}S} 2}} \right. \kern-0em} 2}$, где $\rho $ — плотность жидкости, $S$ – площадь крыла. Усредненный по периоду коэффициент ${{C}_{{{{T}_{i}}}}}$ равен коэффициенту ${{C}_{T}}$. Отметим, что коэффициентом $\eta $ называется отношение средней полезной мощности, равной произведению усредненной по периоду силы тяги на скорость набегающего потока к средней за период колебаний мощности, затрачиваемой на осуществление колебательного движения крыла.
На рис. 5 графически представлены зависимости коэффициента силы тяги ${{C}_{T}}$ и гидродинамического коэффициента полезного действия $\eta $ от частоты колебаний $\omega {\kern 1pt} {\text{'}}$ в случае, когда ось угловых колебаний проходит через точку передней кромки корневого сечения крыла $(b_{0}^{{\text{'}}} = 0)$, а амплитуда колебаний $h{\kern 1pt} ' = 1.0$. При таком расположении оси для крыла 1 коэффициент ${{C}_{T}}$ растет, а коэффициент $\eta $ убывает с ростом частоты колебаний. При этом коэффициент силы тяги невелик $({{C}_{T}} \approx 0.25)$.
Рис. 5.
Зависимости коэффициента силы тяги ${{C}_{T}}$ и гидродинамического коэффициента полезного действия $\eta $ от частоты колебаний $\omega {\kern 1pt} {\text{'}}$ при $h{\kern 1pt} ' = 1.0$, когда ось угловых колебаний проходит через точку передней кромки (рис. 5, здесь $b_{0}^{{\text{'}}} = 0$) и задней кромки (рис. 6, на задней кромке $b_{0}^{{\text{'}}} = 1$) корневого сечения крыла.
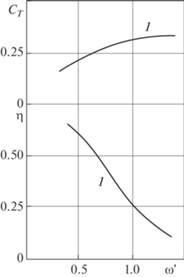
На рис. 6 представлены зависимости ${{C}_{T}} = {{C}_{T}}(\omega {\kern 1pt} {\text{'}})$ и $\eta = \eta {\kern 1pt} (\omega {\kern 1pt} ')$ при $h{\kern 1pt} ' = 1.0$ в случае, когда ось угловых колебаний проходит через точку задней кромки корневого сечения крыла $(b_{0}^{{\text{'}}} = 1)$. Графики показывают, что при изменении $h{\kern 1pt} '$ в пределах от 0.5 до 1.5 происходит качественное изменение характера зависимости коэффициента полезного действия крыла 1 от частоты его колебаний. Так, коэффициент ${{\eta }}$ при $h{\kern 1pt} ' = 0.5$ (кривая 1) с увеличением частоты монотонно возрастает. При $h{\kern 1pt} ' \approx 1.0$ и $h{\kern 1pt} ' = {\text{1}}{\text{.5}}$ (кривые 2, 3) зависимости $\eta {\kern 1pt} (\omega )$ оказываются немонотонными. При этом с увеличением амплитуды колебаний частота, при которой $\eta $ имеет максимальное значение, уменьшается:
(3)
$\begin{gathered} \max \eta {\kern 1pt} (h{\kern 1pt} ' = 1.5,\omega {\kern 1pt} {\text{'}}) \equiv \max \eta {\kern 1pt} (h{\kern 1pt} ' = 1.5,\omega _{1}^{{\text{'}}}) < \\ < \max \eta {\kern 1pt} (h{\kern 1pt} ' = 1.0,\omega {\kern 1pt} {\text{'}}) \equiv \max \eta {\kern 1pt} (h{\kern 1pt} ' = 1.0,\omega _{2}^{{\text{'}}}), \\ \max \eta {\kern 1pt} (h{\kern 1pt} ' = 1.0,\omega {\kern 1pt} {\text{'}}) \equiv \max \eta {\kern 1pt} (h{\kern 1pt} ' = 1.0,\omega _{2}^{{\text{'}}}) < \\ < \max \eta {\kern 1pt} (h{\kern 1pt} ' = 0.5,\omega {\kern 1pt} {\text{'}}) \equiv \max \eta {\kern 1pt} (h{\kern 1pt} ' = 0.5,\omega _{3}^{{\text{'}}}), \\ \omega _{1}^{{\text{'}}} < \omega _{2}^{{\text{'}}} < \omega _{3}^{{\text{'}}}. \\ \end{gathered} $Рис. 6.
Зависимости коэффициента силы тяги ${{C}_{T}}$ и гидродинамического коэффициента полезного действия $\eta $ от частоты колебаний $\omega {\kern 1pt} {\text{'}}$ при $h{\kern 1pt} ' = 1.0$, когда ось угловых колебаний проходит через точку передней кромки (рис. 5, здесь $b_{0}^{{\text{'}}} = 0$) и задней кромки (рис. 6, на задней кромке $b_{0}^{{\text{'}}} = 1$) корневого сечения крыла.

На рис. 6 все графики коэффициента силы тяги от частоты колебаний представляют собой возрастающие функции, которые увеличиваются с ростом $\omega {\kern 1pt} '$ тем быстрее, чем больше $h{\kern 1pt} '$. Наибольшие значения коэффициента силы тяги ${{C}_{T}}$ крыла 1 достигаются при наибольших значениях амплитуды $h{\kern 1pt} '$ и частоты $\omega {\kern 1pt} '$. Из анализа кривых на рис. 5, 6 следует, что колебания с бóльшими амплитудами ($h{\kern 1pt} ' = 1.0$, $h{\kern 1pt} ' = {\text{1}}{\text{.5}}$) предпочтительнее колебаний с малыми амплитудами ($h{\kern 1pt} ' = 0.5$) для получения бóльших значений коэффициента силы тяги. В продолжение анализа кривых на рис. 5 с графиками рис. 6 отметим, что коэффициенты ${{C}_{T}}$ и $\eta $ крыла 1 в случае $b_{0}^{{\text{'}}} = 0$ много меньше, чем в случае $b_{0}^{{\text{'}}} = 1$.
Представляет интерес исследование формирования свободной вихревой поверхности за колеблющимся крылом. Такое исследование усложняется необходимостью трехмерного рассмотрения обтекания. Поэтому ограничимся рассмотрением свободной вихревой поверхности в плоскости симметрии течения ${{x}^{2}} = 0$ крыла 1, колеблющегося при значениях параметров: $h{\kern 1pt} ' = 1$, $b_{0}^{{\text{'}}} = 1$, $\omega {\kern 1pt} {\text{'}} = 1$ (рис. 7). Следует отметить, что в сечении ${{x}^{2}} = 0$ в силу симметричного обтекания крыла компонент $\gamma _{w}^{1}$ вектора ${{\vec {\gamma }}_{w}}$ тождественно равен нулю.
Рис. 7.
Положения координатной линии ${{b}^{2}} = 0$ свободной вихревой поверхности в моменты времени $\tau = 2\pi $ и $\tau = 3\pi $ (рис. 7а); точками на рисунке показаны узловые точки расчетной сетки координатной линии ${{b}^{2}} = 0$, рядом с точками приведены их лагранжевы координаты $b_{\nu }^{1} = \nu {\text{,}}\nu = 0,1,2,...$. Структура свободной вихревой поверхности за крылом представлена на рис. 7б.
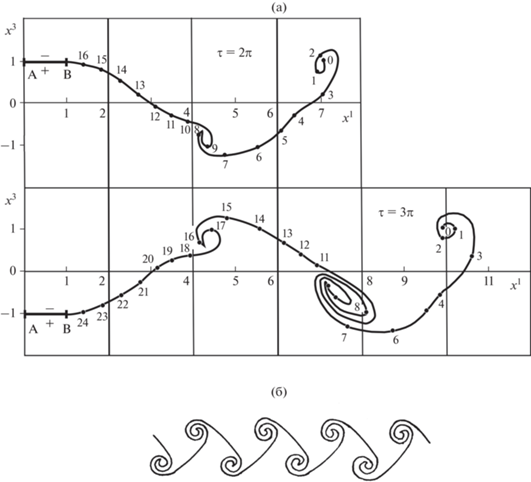
Показанные на рис. 7 положения координатной линии ${{b}^{2}} = 0$ свободной вихревой поверхности в моменты времени $\tau = {{\pi i} \mathord{\left/ {\vphantom {{\pi i} 2}} \right. \kern-0em} 2},{\text{ }}i = 4,6$ ($\tau = \omega t$ – безразмерное время) позволяют проследить развитие во времени свободной вихревой поверхности в плоскости симметрии течения ${{x}^{2}} = 0$. На рис. 7а отрезком $AB$ изображена корневая хорда крыла (точка $A$ соответствует кромке натекания корневой хорды). Крыло занимает, соответственно, крайние верхнее и нижнее положения в моменты времени $\tau = 2\pi i,\,\,i = 0,1,2,...$ и $\tau = (2j + 1)\pi ,{\text{ }}j = 1,2,...$ Точками на рисунке показаны узловые точки расчетной сетки координатной линии ${{b}^{2}} = 0$ [7]. На этом рисунке приведены и лагранжевы координаты $b_{\nu }^{1} = \nu $ ($\nu = 0,1,2,...$) узловых точек координатной линии ${{b}^{2}} = 0$.
Анализ результатов расчета показывает, что с течением времени свободная вихревая поверхность закручивается вокруг точек, в которых интенсивность завихренности максимальна по абсолютной величине. Из рис. 7а видно, что участки свободной вихревой поверхности с лагранжевыми координатами $b_{\nu }^{1} \approx 0{\kern 1pt} - {\kern 1pt} 3$ и $b_{\nu }^{1} \approx 15{\kern 1pt} - {\kern 1pt} 17$ закручиваются против часовой стрелки (в этих точках $\gamma _{w}^{2} < 0$, причем в точках $b_{\nu }^{1} = 2$ и $b_{\nu }^{1} = 16$ зависимость $\gamma _{w}^{2} = \gamma _{w}^{2}({{b}^{1}})$ имеет локальные минимумы), а участок свободной вихревой поверхности с лагранжевыми координатами $b_{\nu }^{1} \approx 7{\kern 1pt} - {\kern 1pt} 10$ закручивается по часовой стрелке (в этих точках $\gamma _{w}^{2} > 0$ и точка $b_{\nu }^{1} = 8$ является точкой локального максимума).
Таким образом, после установления периодического режима обтекания крыла 1, приведенного в движение из состояния покоя, структура свободной вихревой поверхности в плоскости симметрии течения имеет вид, схематически показанный на рис. 7б.
Сравнение расчета с экспериментальными данными [3, 10] позволяет предположить, что дельфины двигаются с наибольшим значением коэффициента полезного действия. В экспериментах [3, 10], как отмечено выше, определялись амплитуда и частота колебаний точки у развилки хвостового плавника дельфина. Если предположить, что движение хвостового плавника дельфина описывается законом (2) с осью угловых колебаний, совпадающей с задней кромкой, то амплитуда и частота будут амплитудой и частотой оси угловых колебаний модели хвостового плавника. (Здесь предположение о локализации оси угловых колебаний является естественным, поскольку из расчетных данных, приведенных на рис. 5, 6, следует, что для движения с наибольшим значением коэффициента $\eta $ ось угловых колебаний должна располагаться вблизи задней кромки). В указанных экспериментах в основном наблюдались амплитуда и частота колебаний точки у развилки хвостового плавника, соответствующие $h{\kern 1pt} ' \approx 1.0;$ $\omega {\kern 1pt} {\text{'}} \approx 1.1$ [10] и $\omega {\kern 1pt} {\text{'}} \approx 0.9$ [3].
Расчеты, проиллюстрированные на рис. 6, показывают, что в случае $b_{0}^{{\text{'}}} = 1$ наибольшее значение гидродинамического коэффициента полезного действия $\eta $ крыла 1 достигается при $h{\kern 1pt} ' = 1.0$ и $\omega {\kern 1pt} {\text{'}} = 1.15$ (кривая 2). На рис. 8 на поверхности $\eta = \eta {\kern 1pt} (\omega {\kern 1pt} {\text{'}},h{\kern 1pt} ')$ выделена точка $М$, соответствующая наибольшему значению коэффициента $\eta $ крыла 1, которое достигается при указанных значениях параметров $h{\kern 1pt} '$ и $\omega {\kern 1pt} {\text{'}}$.
Рис. 8.
Поверхность $\eta = \eta {\kern 1pt} (\omega {\kern 1pt} ',h{\kern 1pt} ')$ с выделенной точкой $М$, соответствующей максимальному значению коэффициента $\eta $ крыла 1, которое достигается при $h{\kern 1pt} ' = 1.0$ и $\omega {\kern 1pt} {\text{'}} = 1.15$.
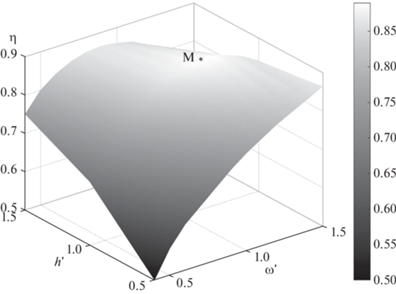
Таким образом, результаты расчетов для крыла 1 находятся в согласии с предположением о том, что дельфины при длительном движении с постоянной скоростью используют наиболее рациональный механизм движения. В этом случае максимально возможная часть затрачиваемой на колебания хвостового плавника мощности расходуется на производство полезной работы по перемещению тела животного. В работах [3, 10] получено, что с увеличением амплитуды колебаний хвостового плавника у дельфинов наблюдается тенденция к уменьшению частоты колебаний. Согласно графикам на рис. 6, с гидродинамической точки зрения это происходит по той причине, что при увеличении амплитуды колебаний наибольшее значение коэффициента $\eta $ естественно достигается при более низких частотах колебаний.
Следовательно, можно считать, что гидродинамическая модель хвостового плавника с формой в плане, близкой к форме хвостового плавника дельфина, удовлетворительно описывает имеющиеся экспериментальные данные о кинематике плавания дельфинов.
Пониманию механизма образования силы тяги хвостового плавника способствует анализ зависимости мгновенного коэффициента силы тяги от времени и выяснение роли вкладов в эту зависимость подсасывающей силы и силы за счет перепада давлений на крыле. На рис. 9 сплошной линией показана зависимость мгновенного коэффициента ${{C}_{{{{T}_{i}}}}}$ крыла 1 от времени $\tau $ при $h{\kern 1pt} ' = 1$, $b_{0}^{{\text{'}}} = 1$, $\omega {\kern 1pt} {\text{'}} = 1$, а штриховой линией – вклад подсасывающей силы. Видно, что сила тяги хвостового плавника создается совместным действием двух механизмов, взаимно дополняющих друг друга. Утолщенная закругленная передняя кромка хвостового плавника дельфина обеспечивает создание подсасывающей силы необходимой величины на той части периода, где ослабляет работу механизм силы тяги за счет перепада давлений и даже где последняя вместо силы тяги становится силой торможения.
ЗАКЛЮЧЕНИЕ
Расчеты показывают, что в процессе длительной эволюции и естественного отбора у дельфинов развился и закрепился тот механизм движения, который определялся критерием наибольшей эффективности действия локомоторных органов дельфина и оптимальным использованием различных способов создания силы тяги.
Список литературы
Зайцев А.А., Федотов А.А. Обтекание идеальной несжимаемой жидкостью тонкого крыла конечного размаха, колеблющегося с большой амплитудой // Изв. АН СССР. МЖГ. 1986. № 5. С. 75–82.
Каян В.П. О гидродинамических характеристиках плавникового движителя дельфина // Бионика. 1979. Вып. 13. С. 9–15.
Каян В.П., Пятецкий В.Е. Кинематика плавания дельфина афалины в зависимости от режима ускорения // Бионика. 1977. Вып. 11. С. 36–41.
Каян В.П., Пятецкий В.Е. Гидродинамические характеристики дельфина афалины при различных режимах ускорения // Бионика. 1978. Вып. 12. С. 48–55.
Козлов Л.Ф. Теоретическая биогидродинамика. Киев: Выс. шк., 1983. 238 с.
Краснов Н.Ф. Аэродинамика. М.: Высш. шк., 1980. Ч. I. 495 с.
Крылов Д.А., Сидняев Н.И., Федотов А.А. Обтекание колеблющегося крыла потоком идеальной несжимаемой жидкости // Труды МГТУ им. Баумана. 2013. № 608. С. 74–92.
Першин С.В. О резонансном режиме плавания дельфинов // Бионика. 1970. № 4. С. 31–36.
Першин С.В. Гидродинамический анализ профилей плавников дельфинов и китов // Бионика. 1975. Вып. 1. С. 26–32.
Пятецкий В.Е., Каян В.П. О кинематике плавания дельфина–афалины // Бионика. 1975. Вып. 9. С. 41–46.
Пятецкий В.Е., Шакало В.М., Циганюк А.И. и др. Исследование режима обтекания водных животных // Бионика. 1982. Вып. 16. С. 31–37.
Томилин А.Г. Снова в воду: Биологический очерк об околоводных, полуводных и водных млекопитающих. М.: Знание, 1984. 192 с.
Федотов А.А. Эффективность работы хвостового плавникового движителя // Докл. АН СССР. 1987. Т. 293. № 1. С. 48–51.
Федотов А. А. Структура вихревого следа за крылом, работающим в режиме нормального трепещущего полета // Вестник МГУ. Сер. 1. Матем. Мех. 1990. № 3. С. 42–46.
Lighthill M.J. Hydromechanics of aquatic animal propulsion // Ann. Rev. Fluid Mech. 1969. V. 1. P. 413–446. (Рус. перев.: Лайтхилл Дж. Гидромеханика движения водных животных // Сб. переводов “Механика”. 1972. № 1. С. 80–109).
Wu Т.Y. Introduction to the scaling of aquatic animal locomotion // In: Scale effects in animal locomotion (ed. T. Pedley). London: Academic Press, 1977. P. 203–232. (Рус. пер.) О масштабном эффекте для передвижения водных животных // Механика. Новое в зарубежной науке. № 23. Биогидродинамика плавания и полета. М.: Мир, 1980. С. 79–112).
Дополнительные материалы отсутствуют.