Океанология, 2023, T. 63, № 3, стр. 467-474

ВВЕДЕНИЕ

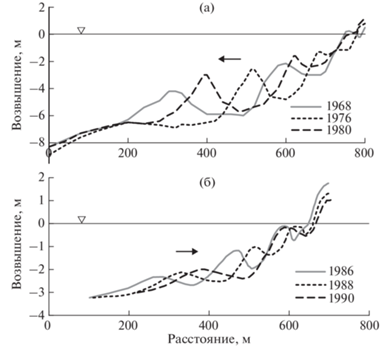
Характерной чертой морфологии песчаного аккумулятивного берега являются волнообразные структуры разного масштаба, которые прослеживаются как в рисунке береговой линии, так и в очертаниях профиля берегового склона. К ритмическим формам контура берега относятся, например, береговые фестоны, песчаные волны и песчаные косы с пространственным шагом от десятков метров до нескольких километров. Что касается профиля берега, то наиболее наглядным примером периодических структур служат системы подводных валов (рис. 1). Их шаг, измеряющийся десятками и сотнями метров, обычно увеличивается с удалением от берега, хотя при определенных условиях может оставаться более или менее постоянным.

Для объяснения феномена ритмических форм прибрежной морфологии предложено множество гипотез и теорий, которые можно условно разделить на две группы. Теории первой группы в качестве главной причины рассматривают гидродинамические воздействия, обладающие собственным пространственным ритмом, который в конечном счете передается и прибрежному рельефу. Так, предполагается, что за периодические структуры контура берега могут быть ответственны краевые волны (edge waves) [7]. Аналогичным образом развитие систем подводных валов связывается с инфрагравитационными колебаниями различной природы. При отражении от берега они создают чередующиеся зоны конвергенции и дивергенции придонных течений [15], а также вызывают флуктуации скорости диссипации энергии [1], что может отражаться в рельефе дна.

Теории второй группы, получившие в настоящее время наибольшее признание, основываются на идее о самоорганизации прибрежной морфологии как нелинейной системы с положительной обратной связью между гидродинамикой и эволюционирующим рельефом дна [9, 10, 12, 13]. Пространственный ритм рельефа в этом случае не совпадает с ритмом вынуждающих сил, а вырабатывается в процессе их взаимодействия. Прямолинейный берег и плоский подводный склон оказываются неустойчивыми, и небольшое возмущение рельефа с подходящей длиной волны может увеличиваться со временем, вызывая пространственные осцилляции контура и профиля берега. Модели самоорганизации рельефа позволяют оценить размер циркуляционных ячеек [18], пространственный шаг песчаных волн [12] и мегафестонов [3], а также описать эволюцию ритмических форм береговой линии [6].

Однако роль самоорганизации в формировании подводных валов пока не вполне ясна. Данный механизм, по-видимому, причастен к развитию одиночного вала в зоне обрушения волн [19]. С другой стороны, подобный вал неплохо воспроизводится морфодинамическими моделями, в которых рассматриваемый механизм непосредственно не задействован [2]. Вместе с тем, развитие и поведение мульти-валовых систем, наблюдаемых на песчаных морских берегах, едва ли может быть объяснено без учета самоорганизации прибрежной морфологии [22].

Цель настоящей работы заключается в том, чтобы выяснить, при каких условиях механизм самоорганизации рельефа может быть ответственен за формирование подводных валов. Речь идет об условиях, при которых возникшее волнообразное возмущение профиля дна будет развиваться со временем. Предложенное решение проблемы основывается на аналитической модели, использующей принцип сохранения массы и упрощенную схему поперечного транспорта наносов на береговом склоне. При интерпретации полученных результатов принимаются во внимание имеющиеся данные наблюдений за поведением подводных валов.

РАСХОД НАНОСОВ И ДИССИПАЦИЯ ЭНЕРГИИ

В основе рассматриваемой модели лежит закон сохранения массы, который связывает изменения локальной глубины с градиентом расхода наносов, и при однородных вдоль берега условиях записывается в виде

Здесь $h$ – глубина, $t$ – время, $x$ – горизонтальное расстояние (ось OX направлена к берегу), $q$ – поперечный к изобатам объемный расход наносов на единицу ширины (м³ м^–1 с^–1), создаваемый волнами и связанными с ними течениями. Для определения $q$ воспользуемся подходом [16], согласно которому поперечный расход пропорционален разности локальной скорости диссипации энергии на единицу объема $D$ и некоторой постоянной величины ${{D}_{*}}$, отвечающей состоянию равновесия профиля: Здесь $K$ и $\epsilon $ – коэффициенты пропорциональности (1.1 × 10^–6 м⁴ н^–1 и 0.0006 м³ м^–1 с^–1 соответственно [16]), ${{\Phi }_{d}}$ – функция направления, принимающая значения 1 (перенос к берегу) или –1 (перенос от берега). Второе слагаемое в правой части представляет вклад силы тяжести, заставляющей наносы перемещаться вниз по склону (если дно повышается к берегу, то $\frac{{\partial h}}{{\partial x}} < 0$).

Для идентификации направления переноса может быть использован безразмерный параметр Дина $\Omega = {{{{H}_{{s0}}}} \mathord{\left/ {\vphantom {{{{H}_{{s0}}}} {\left( {{{w}_{g}}{{T}_{p}}} \right)}}} \right. \kern-0em} {\left( {{{w}_{g}}{{T}_{p}}} \right)}}$, где ${{H}_{{s0}}}$ – значительная высота волн на глубокой воде, ${{w}_{g}}$ – скорость осаждения частиц песка, связанная с их размером, ${{T}_{p}}$ – период спектрального пика волн [11]. Условие $\Omega > {{\Omega }_{0}}$, где ${{\Omega }_{0}} \approx 1.5$, определяет размыв пляжа и отток наносов от берега (${{\Phi }_{d}} = - 1$), а условию $\Omega < {{\Omega }_{0}}$ отвечает приток материала к берегу (${{\Phi }_{d}} = 1$) и нарастание пляжа. Данный критерий отражает эмпирическую закономерность, согласно которой действие крутых штормовых волн вызывает интенсивное взвешивание песка и вынос его противотечением в сторону моря, тогда как в условиях менее крупных и более пологих волн наносы перемещаются к берегу под влиянием асимметрии волновых скоростей.

Диссипация энергии $D$ связана, главным образом, с обрушением волн, вызывающим уменьшение потока волновой энергии $F$:

где $\rho $ – плотность воды, $g$ – ускорение силы тяжести, $H$ – высота волн.

Изменения $H$ в прибойной зоне нередко аппроксимируются моделью бора, высота которого пропорциональна глубине, уменьшающейся к берегу:

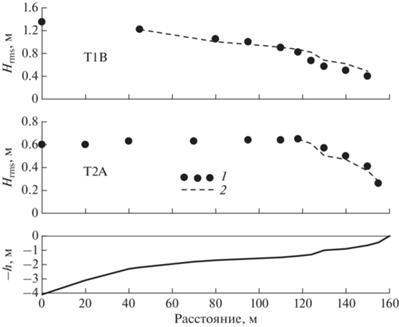
где ${{H}_{B}}$ и ${{h}_{B}}$ – высота волн и глубина в точке обрушения. На рис. 2 представлены изменения среднеквадратичной высоты нерегулярных волн ${{H}_{{rms}}}$ над песчаным береговым склоном, измеренные в волновом канале при различных исходных параметрах волн [5]. Хотя затухание волн в области диссипации, в общем, следует уменьшению глубин, наблюдаемый тренд в большей мере соответствует зависимости вида которая также приведена на рис. 2 для $m = {3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}$. В качестве ${{H}_{B}}$ и ${{h}_{B}}$ здесь приняты значения ${{H}_{{rms}}}$ и $h$, зафиксированные перед уменьшением высот волн в относительно мелководной части профиля.

Аппроксимация (5), как и (4), предполагает уменьшение глубин к берегу $\left( {\frac{{\partial h}}{{\partial x}} < 0} \right)$. Применив (5) с $m = {3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}$ к соотношениям (3), получим

где $\gamma = {{{{H}_{B}}} \mathord{\left/ {\vphantom {{{{H}_{B}}} {{{h}_{B}}}}} \right. \kern-0em} {{{h}_{B}}}} \approx 0.4$, если подразумевается среднеквадратичная высота нерегулярных волн ${{H}_{{rmsB}}}$ [17]. Заметим, что в рамках нашей упрощенной модели условие $D = {{D}_{*}} = {\text{const}}$ приводит к линейному профилю равновесия, $h = \bar {\beta }\left( {{{l}_{B}} - x} \right)$, где $\bar {\beta } = {{{{h}_{B}}} \mathord{\left/ {\vphantom {{{{h}_{B}}} {{{l}_{B}}}}} \right. \kern-0em} {{{l}_{B}}}}$ – средний уклон дна, ${{l}_{B}}$ – длина области диссипации энергии.

Согласно (6) и (2), величина поперечного расхода наносов $q$ оказывается прямо пропорциональной уклону дна $\beta = - \frac{{\partial h}}{{\partial x}}$.

ЭВОЛЮЦИЯ ВОЗМУЩЕНИЯ ПРОФИЛЯ ДНА

Приняв во внимание (6), продифференцируем $q$ по $x$ и подставим результат в уравнение (1). В итоге придем к уравнению диффузии:

где ${{\nu }_{D}}$ имеет смысл коэффициента диффузии.

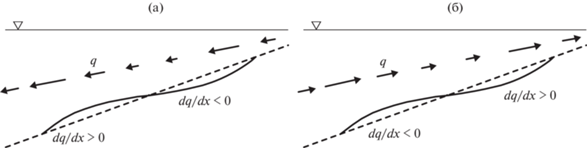
Допустим, что на плоском наклонном дне возникает волнообразное возмущение в виде вала и ложбины (рис. 3) с очень малой амплитудой $a$ и волновым числом $k = \frac{{2\pi }}{\lambda }$, где $\lambda $ – длина возмущения. Тогда профиль глубин можно представить как

Вопрос заключается в том, будет ли возмущение затухать или, наоборот, его амплитуда $a$ будет увеличиваться со временем. Подставив (8) в (7) получим уравнение, определяющее изменение амплитуды возмущения: Его решение имеет вид где ${{a}^{{\left( 0 \right)}}}$ – начальная амплитуда возмущения (в момент $t$ = 0).

Тенденция изменения $a$, очевидно, зависит от знака величины ${{\nu }_{D}}$. Если ${{\nu }_{D}} < 0$, то возмущение затухает, а при ${{\nu }_{D}} > 0$ его амплитуда растет со временем. В первом случае наносы должны перемещаться от берега в море (${{\Phi }_{d}} = - 1$). Рост возмущения, напротив, возможен только при транспортировке материала к берегу (${{\Phi }_{d}} = 1$).

В случае ${{\nu }_{D}} > 0$, согласно (10), быстрее всего растут флуктуации с наименьшей длиной $\lambda $. Однако ясно, что $\lambda $ не может быть меньше расстояния, на котором расход наносов успевает отреагировать на изменения обстановки (вероятно, расстояние порядка глубины ${{h}_{B}}$). С другой стороны, $\lambda $ не должно превышать размер области диссипации энергии (для пологого берега порядка 10²${{h}_{B}}$). Оптимальный масштаб $\lambda $ должен находиться где-то в середине обозначенного интервала.

Масштаб времени $t$, в течение которого малое возмущение рельефа может достичь заданного размера, определяется из (10) как

В соответствии с (7), где подразумевается ${{\Phi }_{d}} = 1$, коэффициент диффузии при умеренном волнении (${{H}_{{rmsB}}}$ = 1 м) характеризуется величиной ${{\nu }_{D}}$ = = 0.021 м²/с. Тогда возмущение с начальной высотой $2{{a}^{{\left( 0 \right)}}}$ = 0.01 м и длиной, например, $\lambda $ = 50 м сможет достичь высоты $2a$ = 1 м за период времени $t \approx 4$ ч. Реальный период должен быть больше, так как по мере приближения к равновесию рост структуры будет замедляться. Тем не менее, можно заключить, что время формирования вала сравнимо с характерной продолжительностью отдельных волнений.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Для физической интерпретации полученных результатов рассмотрим изменения расхода наносов $q$ над волнообразной структурой, возникшей на плоском наклонном дне (рис. 3), имея в виду, что рамках нашей модели величина $q$ прямо пропорциональна уклону дна.

В случае, когда перенос направлен от берега в море (рис. 3а), расход наносов над возникшей ложбиной затухает в силу уменьшения локального уклона дна, а значит, ложбина заполняется осаждающимся материалом. На выпуклом участке дна уклон увеличивается и расход возрастает, что ведет к размыву появившейся структуры и сглаживанию рельефа.

Если же наносы транспортируются к берегу (рис. 3б), то расход над выпуклым участком дна сначала увеличивается, а затем уменьшается, следуя изменению уклона, что, в свою очередь, вызывает аккумуляцию материала и рост структуры. Следовательно, возникает положительная обратная связь между транспортом наносов и рельефом, которая является необходимым условием для действия механизма самоорганизации рельефа.

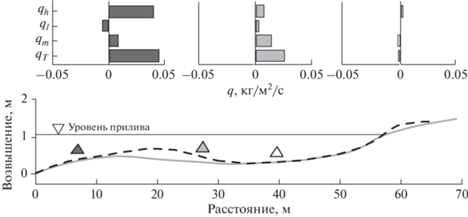
Соответствующий пример, зафиксированный измерениями на голландском побережье Северного моря в условиях зыби с относительно большим периодом, показан на рис. 4 [8]. Как видно, расход движущихся к берегу наносов уменьшается при прохождении над валом, что способствует его росту.

Возвращаясь к рис. 3, заметим, что принципиальным для роста возмущения является перенос в сторону берега над его внешним склоном, тогда как направление переноса в остальной части профиля не так важно. Например, действие оттока в области, расположенной ближе к берегу, только ускорило бы формирование вала вследствие конвергенции потоков у его вершины. Подобная ситуация характерна для штормового волнения, при котором материал, смытый с пляжа, транспортируется противотечением. Сам по себе поток вниз по склону подавляет развитие возмущений на дне (рис. 3а), но действие встречного потока заставляет наносы аккумулироваться в форме вала.

Таким образом, вал в зоне обрушения крутых штормовых волн может трактоваться как форма, созданная двумя механизмами – самоорганизации и конвергенции потоков. Необходимым условием для поддержания вала является движение наносов к берегу во внешней части области диссипации. О том же свидетельствуют данные измерений в волновом канале [14], согласно которым, даже в случае доминирующего оттока взвешенного материала и перемещении самого вала в сторону моря в ходе шторма, транспорт донных наносов (bed-load) на внешнем склоне вала продолжает оставаться направленным в сторону берега.

Принимая во внимание полученные результаты, попытаемся интерпретировать некоторые известные свойства мульти-валовых систем. Наблюдениями на берегах Северного моря установлено, что такие системы испытывают циклические изменения с периодом порядка 10 лет (рис. 1). На побережье Голландии (район Эгмонд, рис. 1а) основным районом генерации валов оказывается область вблизи берега с глубинами 1–2 м. Возникший здесь вал постепенно смещается в сторону моря, увеличиваясь в размерах, но на глубинах более 7 м он деградирует, что дает начало новому циклу [20, 21].

На западном побережье Дании (район Скаллинген, рис. 1б) наблюдается противоположный тип эволюции [4]. Вал зарождается вдали от берега (на глубинах около 4 м), затем постепенно мигрирует в сторону берега и в конце концов примыкает к пляжу, что открывает новый цикл.

Причины столь различного поведения мульти-валовых систем пока не ясны. Возможно, имеет значение то обстоятельство, что береговой склон в Голландии примерно вдвое круче, чем в Дании (соответствующие уклоны дна около 0.01 и 0.005), и направление перемещения валов, вероятно, зависит от степени влияния силы тяжести.

Общая особенность заключается в том, что области генерации валов располагаются за пределами зоны обрушения штормовых волн. Это области воздействия на дно либо слабого волнения, либо сравнительно крупных волн, основная масса которых еще не начала обрушаться. В обоих случаях создаются благоприятные условия для транспорта наносов в сторону берега, так как доминирующим фактором переноса служит асимметрия волновых скоростей. Соответственно появление первичного вала, скорее всего, объясняется механизмом самоорганизации, который, к тому же, служит триггером для запуска очередного цикла.

Дальнейший рост вала по мере его смещения и приближения к зоне обрушения штормовых волн, по-видимому, обусловлен как увеличением объемов перемещающихся наносов, так и подключением дополнительного механизма аккумуляции, связанного с конвергенцией потоков. За пределами района обрушения данный механизм перестает действовать, потоки материала уменьшаются, и то же происходит и с самим валом.

К еще одному типу мульти-валовых систем относятся, так называемые, множественные параллельные валы, которые развиваются на защищенных пологих берегах с низким уровнем поступающей энергии (лагуны, эстуарии, бухты). Системы валов высотой порядка первых десятков см характеризуются примерно одинаковым шагом порядка 10 м и насчитывают иногда более десятка элементов [22]. Каких-либо объяснений данному феномену не существует. Однако слабая энергетика подразумевает доминирование переноса осадков к берегу, и в соответствии с нашей моделью развитие валов в данных условиях можно связать только с самоорганизацией рельефа.

ЗАКЛЮЧЕНИЕ

Формирование прибрежного рельефа в значительной мере зависит от механизма самоорганизации, суть которого в том, что взаимодействие гидродинамики и рельефа способно дать толчок к росту малого возмущения на дне. До сих пор не выработано четкого представления о том, при каких условиях данный механизм может способствовать развитию подводных валов. Для выяснения этого вопроса в настоящей работе используется упрощенная модель поперечного транспорта наносов (по профилю берега), в которой величина расхода наносов в области диссипации энергии ставится в прямую зависимость от локального уклона дна. Это позволяет свести задачу к аналитическому решению уравнения диффузии, на основании которого удается судить об эволюции возникшего на дне возмущения.

Проведенное исследование приводит к выводу, что тип эволюции зависит от направления транспорта наносов – в сторону моря или к берегу. В случае переноса от берега флуктуации затухают и рельеф сглаживается. При движении наносов к берегу, наоборот, обнаруживается тенденция к росту возмущения, и создаются благоприятные предпосылки для самоорганизации рельефа и развития подводного вала, который может быть построен в течение нескольких часов.

Перенос к берегу ассоциируется с доминирующим вкладом асимметрии волн в транспортировку наносов. Однако в условиях крутых штормовых волн важную роль играет противотечение, обусловливающее вынос материала с пляжа. В этом случае вал в зоне обрушения формируется двумя механизмами – самоорганизации и конвергенции потоков, причем необходимым условием является сохранение переноса к берегу на внешнем склоне вала.

Имеющиеся данные наблюдений подтверждают возможность развития подводных валов при обозначенных условиях. Полученные результаты помогают связать наблюдаемое циклическое поведение валов с механизмом самоорганизации рельефа, а также объяснить появление мульти-валовых систем на защищенных низко-энергетических берегах.

В дальнейших исследованиях следует ориентироваться на более продвинутые (в том числе, численные) модели волнения и транспорта наносов.

Источник финансирования. Работа выполнена в рамках государственного задания ИО РАН (тема № FMWE-2021-0004).