1. На главную
  2. Электронные версии
  3. Океанология
  4. T. 63, № 4, 2023

Океанология, 2023, T. 63, № 4, стр. 539-547

Оценка климатического тренда гидрофизических характеристик бассейна Пауэлла

А. А. Букатов 1, Н. М. Соловей 1, *, Е. А. Павленко 1

1 Морской гидрофизический институт РАН
299011 Севастополь, ул. Капитанская 2, Россия

* E-mail: nele7@mail.ru

Поступила в редакцию 27.10.2022
После доработки 01.11.2022
Принята к публикации 16.12.2022

Полный текст (PDF)

Аннотация

На основе гидрологических данных 79-го рейса экспедиции НИС “Академик Мстислав Келдыш” (16.01–6.02.2020) и данных World Ocean Database-2018 за январь–февраль с 1975 по 2020 гг. дана оценка тренда динамического состояния вод бассейна Пауэлла моря Уэдделла. В каждом узле четверть-градусной сетки строился линейный тренд рассчитанных величин максимума частоты плавучести и максимума амплитуды вертикальной составляющей скорости внутренних волн. Показано, что юго-западная и северо-западная части бассейна Пауэлла существенно различаются по своим гидрофизическим характеристикам. На северо-западе бассейна линейный тренд максимума частоты плавучести отрицательный, тренды глубин залегания максимальных значений частоты Вяйсяля-Брента и амплитуды вертикальной составляющей скорости положительные. В юго-западной части бассейна тренд максимума частоты плавучести положительный, тренды глубин залегания максимальных значений частоты Вяйсяля-Брента и амплитуды вертикальной составляющей скорости отрицательные.

Ключевые слова: бассейн Пауэлла, частота Вяйсяля-Брента, внутренние волны, вертикальная составляющая скорости, линейный тренд

ВВЕДЕНИЕ

В последние десятилетия отмечаются значительные климатические изменения, которые особенно заметны в высокоширотных регионах. Согласно последнему докладу Межправительственной группы экспертов по изменению климата, оба полярных океана продолжают нагреваться, причем Южный океан играет непропорционально большую и важную роль в глобальном повышении температуры Мирового океана [19].

Из-за сложных ледовых условий моря Южного океана являются наименее изученными регионами, но с появлением искусственных спутников Земли количество наблюдений за различными районами океана значительно увеличилось. Однако они характеризуется значительной пространственной неравномерностью. В высоких широтах спутниковые наблюдения затруднены из-за неподходящих углов падения солнечных лучей на поверхность воды, из-за постоянной облачности и сезонного закрытия поверхности воды льдом [6, 12, 17].

Море Уэдделла – самое большое и глубокое окраинное море атлантического сектора Южного океана у берегов западной Антарктиды, где происходит интенсивное взаимодействие системы океан-атмосфера и вертикальный обмен [14, 18]. С севера оно ограничено хребтом Скотия, на котором расположены дуги Южных Шетландских и Южных Оркнейских островов. С Тихим океаном море соединено проливом Брансфилда. Глубоководный, обособленный от основной котловины моря, бассейн Пауэлла лежит в северо-западной части моря Уэдделла к востоку от пролива Брансфилда. Здесь воды Антарктического циркумполярного течения встречаются с водами круговорота моря Уэдделла. Из-за своего географического положения бассейн Пауэлла играет связующую роль между экосистемами моря Уэдделла, моря Скотия и пролива Брансфилда, обеспечивая накопление и перераспределение криля, поступающего с водами западной ветви круговорота Уэдделла [6, 9, 11, 16].

Внутренние волны (ВВ) играют важную роль в динамике океанов и морей. Они оказывают влияние на процессы горизонтального и вертикального обмена энергией, способствуют перемешиванию вод, обогащению их кислородом и питательными веществами, необходимыми для жизни морских организмов. В настоящей работе на основе экспедиционных и архивных данных дана оценка климатического тренда динамического состояния физической среды бассейна Пауэлла (55°–47° з.д. и 59°–63° ю.ш.).

МАТЕРИАЛЫ И МЕТОДИКА

В работе использовались гидрологические данные, полученные в 79-м рейсе экспедиции НИС “Академик Мстислав Келдыш” (16.01–6.02.2020), и данные World Ocean Database 2018 (WOD 2018). Рассматривался временнóй промежуток с 1975 по 2020 гг., из которого были выбраны 16 лет, наиболее хорошо обеспеченные гидрологическими данными за январь–февраль. Для каждого года создавались массивы осредненных значений температуры и солености в узлах четверть-градусной сетки, по которым рассчитывались профили плотности. Полученные профили тестировались на наличие инверсий и, при необходимости, корректировались путем замены инверсионных величин значениями, интерполированными по соседним горизонтам [1, 13]. Для каждого узла сетки рассчитывался профиль частоты Вяйсяля-Брента (N(z), цикл/час) по формуле

${{N}^{2}}(z) = \frac{g}{\rho }\frac{{d\rho }}{{dz}},$
где z – глубина, g – ускорение свободного падения, ρ – плотность.

Определялся максимум частоты Вяйсяля-Брента по глубине (Nmax(z), цикл/час) и глубина его залегания (${{H}_{{{{N}_{{{\text{max}}}}}\left( z \right)}}}$). Расчеты проводились до глубины 500 м, т.к. в этом слое определяются максимальные значения градиентов температуры и солености (рис. 1 ).

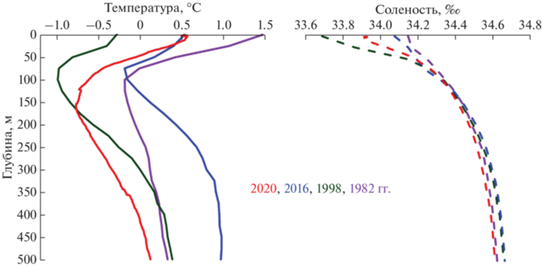
Рис. 1.

Осредненные по акватории бассейна Пауэлла за январь–февраль профили солености и температуры для данных 79-го рейса НИС “Академик Мстислав Келдыш” (2020 г.) и WOD-2018 (1982, 1998, 2016 гг.).

Исследование внутренних волн проводилось исходя из системы линейных уравнений движения непрерывно стратифицированной жидкости в форме Фьельдстада, которая имеет решение в виде суперпозиции плоских волн [8]. В частности, для вертикальной компоненты скорости w(x, y, z, t) (x, y – горизонтальные координаты, t – время) имеет место представление

$\begin{gathered} w\left( {x,y,z,t} \right) = \sum\limits_{n{\kern 1pt} = {\kern 1pt} 1}^\infty {\int {\int\limits_{ - \infty }^\infty {{{W}^{{\left( n \right)}}}\left( {k,z} \right)} } } \times \\ \times \,\,\exp \left\{ {{\kern 1pt} i\left[ {{{k}_{x}}x + {{k}_{y}}y - {{\omega }^{{\left( n \right)}}}\left( k \right)t} \right]{\kern 1pt} } \right\}d{{k}_{x}}d{{k}_{y}}, \\ \end{gathered} $
где ${{\omega }^{{\left( n \right)}}}$(k) – дисперсионное соотношение (собственная частота) для моды c номером n и волновым числом k = ${{(k_{x}^{2} + k_{y}^{2})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$, W (n)(k, z) – амплитуда этой моды (собственная функция). Если использовать приближение Буссинеска, отфильтровать поверхностные волны и пренебречь вращением Земли, то W (n)(k, z) будет решением краевой задачи типа Штурма-Лиувилля с нулевыми граничными условиями на дне и свободной поверхности жидкости:
$\begin{gathered} {{{{d}^{2}}{{W}^{{\left( n \right)}}}} \mathord{\left/ {\vphantom {{{{d}^{2}}{{W}^{{\left( n \right)}}}} {d{{z}^{2}}}}} \right. \kern-0em} {d{{z}^{2}}}} + ({{\lambda }^{{\left( n \right)}}}{{N}^{2}} - {{k}^{2}}){\kern 1pt} {{W}^{{\left( n \right)}}} = 0, \\ {{W}^{{\left( n \right)}}}\left( H \right) = {{W}^{{\left( n \right)}}}\left( 0 \right) = 0, \\ \end{gathered} $
где ${{\lambda }^{{\left( n \right)}}} = {{({k \mathord{\left/ {\vphantom {k {{{\omega }^{{\left( n \right)}}}}}} \right. \kern-0em} {{{\omega }^{{\left( n \right)}}}}})}^{2}}$ – собственное значение, H – глубина.

Данная спектральная задача соответствует определению собственных значений ${{\lambda }^{{\left( n \right)}}}$ и собственных функций W (n)(k, z) для каждого фиксированного значения волнового числа. Для численной реализации краевой задачи по заданному профилю N(z) строилась ее конечно-разностная аппроксимация. Полученная система линейных алгебраических уравнений решалась путем определения корней характеристического многочлена для ее матрицы [2].

Для исследования вертикальной структуры и дисперсионных свойств ВВ рассчитывались собственные значения и собственные функции для длин волн больше 200 м. Описанных в литературе наблюдений ВВ в Антарктическом регионе мало. При выборе интервала длин волн авторы обращались к работам [3, 5, 6], из которых следует, что в высоких широтах на радиолокационных изображениях наблюдаются внутренние волны с длинами > 200 м.

Известно, что первая мода дает наибольший вклад в энергетический спектр пакета волн [7], в связи с этим рассматривались амплитуды вертикальной составляющей скорости (W (1)(k, z)) первой моды свободных внутренних волн. В работе в качестве иллюстрации приведены распределения максимальных значений амплитуды вертикальной составляющей скорости ($W_{{{\text{max}}}}^{{\left( 1 \right)}}\left( {k,z} \right)$) для длины волны 200 м.

АНАЛИЗ РЕЗУЛЬТАТОВ

В результате анализа экспедиционных измерений температуры воды по глубине были зафиксированы две различные по структуре водные массы [10], между которыми простирается четко выраженная фронтальная зона (рис. 2). На северо-востоке бассейна – одна более теплая вода с подповерхностным холодным слоем, типичная для моря Уэдделла, и другая – вода адвективного происхождения, обнаруженная на юго-западе бассейна и поступившая из северо-западной, более мелководной части моря Уэдделла. В северо-западную часть моря Уэдделла из южной части идет большой вынос льда и айсбергов. Плавающий лед не дает возможности солнечной радиации нагревать воду в летнее время, а внутренние волны перемешивают весь слой воды от поверхности до дна [4, 15].

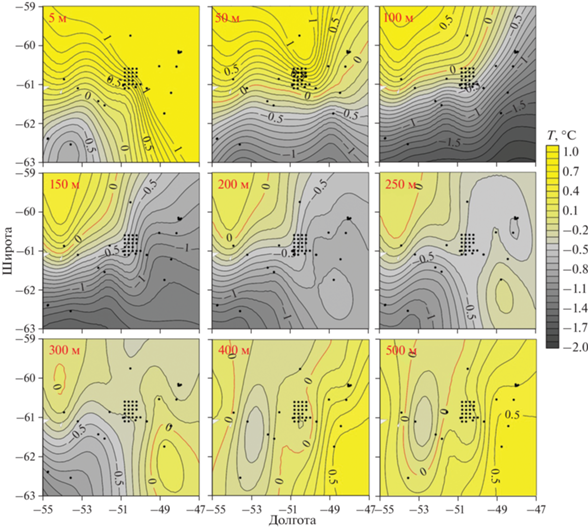
Рис. 2.

Распределение температуры в бассейне Пауэлла на глубинах 5–500 м по данным экспедиции 79-го рейса НИС “Академик Мстислав Келдыш” (точками показаны гидрологические станции).

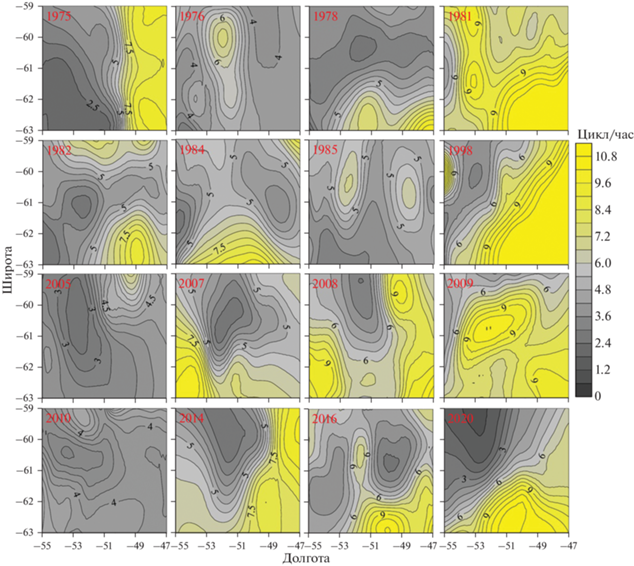
На рис. 3 представлено распределение максимальных значений частоты Вяйсяля-Брента по исследуемой акватории. Видно, что гидрологическая ситуация меняется от года к году, но всегда есть условная граница между наибольшими и наименьшими значениями Nmax(z). Наибольшие значения Nmax(z) фиксируются, как правило, в восточной и юго-восточной частях бассейна Пауэлла. Соответственно, там же определяются наименьшие значения $W_{{{\text{max}}}}^{{\left( 1 \right)}}\left( {k,z} \right)$ (рис. 4).

Рис. 3.

Распределение максимума частоты плавучести в бассейне Пауэлла.

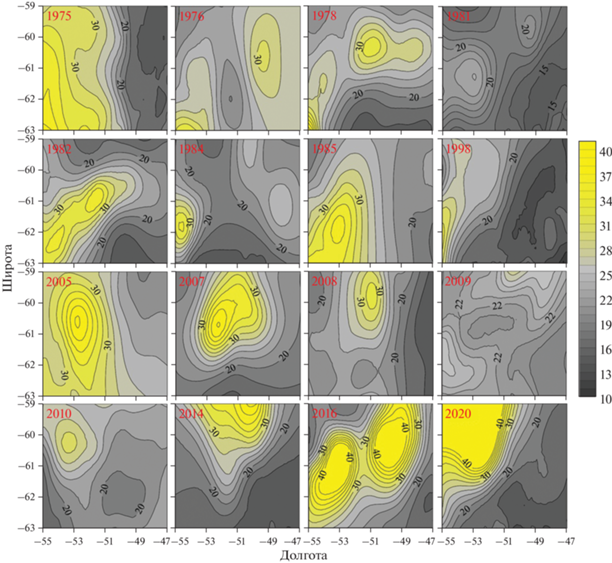
Рис. 4.

Распределение максимума амплитуды вертикальной составляющей скорости свободных ВВ (в условных единицах) в бассейне Пауэлла.

На рис. 5, 6 представлена межгодовая изменчивость вертикальной структуры плотности вод и максимума амплитуды вертикальной составляющей скорости внутренних волн в бассейне Пауэлла на разрезе по 51° з.д. Видно, что наибольшие значения Nmax(z) и наименьшие $W_{{{\text{max}}}}^{{\left( 1 \right)}}\left( {k,z} \right)$ были в 1981, 2009, 2014 и 2020 гг. Отмеченные особенности проявляются на всех рассматриваемых широтах бассейна Пауэлла.

Рис. 5.

Межгодовая изменчивость максимума частоты плавучести на 51° з.д. и количество станций на акватории исследования.

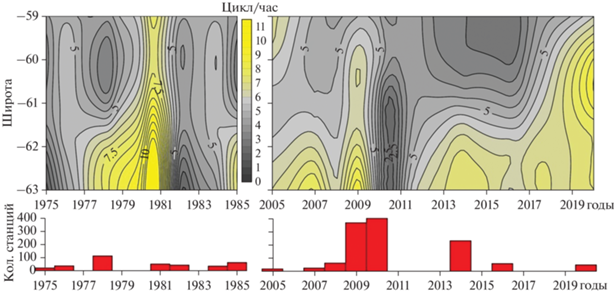
Рис. 6.

Межгодовая изменчивость максимума амплитуды вертикальной составляющей скорости свободных ВВ (в условных единицах) на 51° з.д.

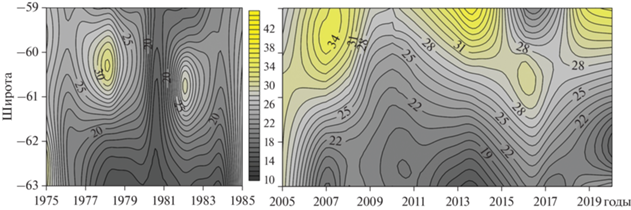
Для оценки пространственно-временнóй изменчивости гидрологических и динамических характеристик вод за весь период исследования в каждом узле сетки рассчитывался линейный тренд максимума частоты плавучести и максимума амплитуды вертикальной скорости ВВ. Рисунок 7 показывает, что в южной части бассейна Пауэлла имеется отрицательный тренд $W_{{{\text{max}}}}^{{\left( 1 \right)}}\left( {k,z} \right)$, а в северной – положительный. И наоборот, в юго-западной части бассейна – положительный тренд Nmax(z), а в северной – отрицательный. В качестве иллюстрации приведены межгодовая изменчивость и тренды Nmax(z) и $W_{{{\text{max}}}}^{{\left( 1 \right)}}\left( {k,z} \right)$ в точках с координатами 54° з.д., 62° ю.ш. (рис. 8) и 52° з.д., 60° ю.ш. (рис. 9). Видно, что тренды имеют разнонаправленный характер. За рассматриваемый период времени максимум частоты Вяйсяля-Брента в точке 54° з.д., 62° ю.ш. увеличился на 2.8 цикл/час, а максимум амплитуды вертикальной составляющей скорости уменьшился на 4.4 у.е. (у.е. – условные единицы, поскольку собственный вектор матрицы всегда определяется с точностью до произвольного множителя [2]). В точке 52° з.д., 60° ю.ш. значение Nmax(z) уменьшилось на 3.2 цикл/час, а $W_{{{\text{max}}}}^{{\left( 1 \right)}}\left( {k,z} \right)$ увеличилась на 15.3 у.е.

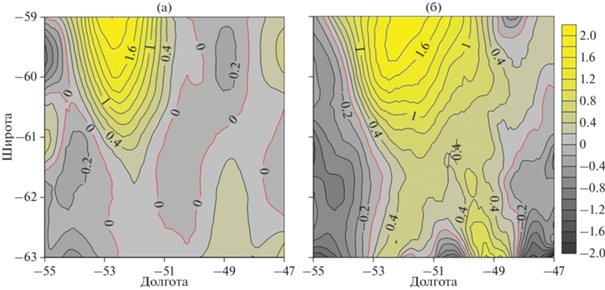
Рис. 7.

Коэффициенты линейных трендов максимума частоты плавучести (а) и максимума амплитуды вертикальной составляющей скорости ВВ (б).

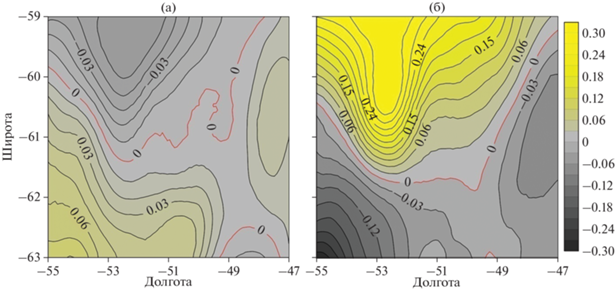
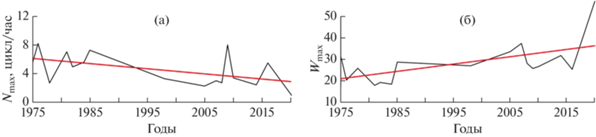
Рис. 8.

Межгодовая изменчивость максимума частоты плавучести (a) и максимума амплитуды вертикальной составляющей скорости ВВ (в условных единицах) (б) в точке 54° з.д., 62° ю.ш. (красная линия – линейный тренд).

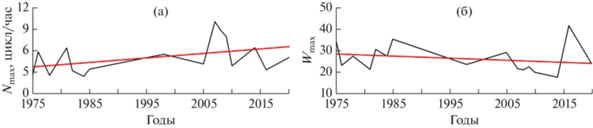
Рис. 9.

Межгодовая изменчивость максимума частоты плавучести (a) и максимума амплитуды вертикальной составляющей скорости ВВ(в условных единицах) (б) в точке 52° з.д., 60° ю.ш. (красная линия – линейный тренд).

Отметим, что наблюдающиеся области с отрицательным трендом максимума частоты плавучести и положительным трендом глубины его залегания характеризуют ослабление стратификации вод в силу различных причин (перемешивание, изменение циркуляции и т.д.) и заглубление максимальных значений градиентов. Скорость заглубления Nmax(z) при этом на порядок превосходит скорость уменьшения величины максимального градиента (рис. 7, 10).

Рис. 10.

Коэффициенты линейных трендов глубин залегания максимума частоты плавучести (a) и максимума амплитуды вертикальной составляющей скорости ВВ (б).

В северной части бассейна Пауэлла линейные тренды $W_{{{\text{max}}}}^{{\left( 1 \right)}}\left( {k,z} \right)$ и ${{H}_{{W_{{{\text{max}}}}^{{\left( 1 \right)}}\left( z \right)}}}$ положительны (рис. 7, 10). Это означает, что существует тенденция увеличения волновой динамики вод и глубины залегания максимальных значений W(1)(k, z) за рассматриваемый временнóй период.

ЗАКЛЮЧЕНИЕ

На основе гидрологических данных, полученных в 79-м рейсе экспедиции НИС “Академик Мстислав Келдыш” и данных WOD-2018 дана оценка климатического тренда динамического состояния физической среды бассейна Пауэлла.

Показано, что юго-западная и северо-западная части бассейна Пауэлла существенно различаются по своим гидрофизическим характеристикам. На северо-западе бассейна преобладает тенденция к уменьшению градиента плотности и увеличению вертикальной динамики вод. В юго-западной части бассейна наоборот – положительный тренд градиента плотности и отрицательный тренд вертикальной составляющей волновой скорости.

Установлено, что в северо-западной части бассейна линейные тренды глубин залегания максимальных значений градиента плотности и амплитуды вертикальной составляющей скорости ВВ положительны, в юго-западной – отрицательны.

Источники финансирования. Работа выполнена в рамках государственного задания по теме № FNNN-2022-0001.

Список литературы

  1. Букатов А.Е., Соловей Н.М. Оценка связи вертикальной структуры поля плотности и характеристик внутренних волн с крупномасштабной атмосферной циркуляцией в акваториях Перуанского и Бенгельского апвеллингов// Процессы в геосредах. 2017. № 2(11). С. 485–490.

  2. Гриценко В.А., Красицкий В.П. Об одном способе расчета дисперсионных соотношений и собственных функций внутренних волн в океане по данным натурных измерений // Океанология. 1982. Т. 22. Вып. 4. С. 546–549.

  3. Зимин А.В., Романенков Д.А., Козлов И.Е. и др. Короткопериодные внутренние волны в Белом море: оперативный подспутниковый эксперимент летом 2012 г. // Исследование земли из космоса. 2014. № 3. С. 41–55.https://doi.org/10.7868/S0205961414030087

  4. Клепиков А.В., Антипов Н.Н. Особенности формирования и распространения водных масс на шельфе и материковом склоне вокруг Антарктиды // Лед и Снег. 2014.54(4). С. 81–94. https://doi.org/10.15356/2076-6734-2014-4-81-94

  5. Козлов И.Е., Кудрявцев В.Н., Зубкова Е.В. и др. Характеристики поля короткопериодных внутренних волн в Карском море по данным спутниковых радиолокационных измерений // Исследование Земли из космоса. 2015. № 4. С. 44–59.https://doi.org/10.7868/S0205961415040053

  6. Краснобородько О.Ю. Внутренние волны в проливе Брансфилд в феврале 2020 года и их влияние на распределение криля // Труды АтлантНИРО. 2021. Т. 5. № 2 (12). Калининград: АтлантНИРО. С. 81−89.

  7. Лобовиков П.В., Куркина О.Е., Куркин А.А., Кокоулина М.В. Трансформация бризера внутренних волн первой моды над вертикальным уступом в трехслойной жидкости // Известия РАН. Физика атмосферы и океана. 2019. Т. 55. № 6. С. 182–193. https://doi.org/10.31857/S0002-3515556182-193

  8. Миропольский, Ю.З., Динамика внутренних гравитационных волн в океане. Л.: Гидрометеоиздат, 1981. 302 с.

  9. Морозов Е.Г., Спиридонов В.А., Молодцова Т.Н. и др. Исследования экосистемы атлантического сектора Антарктики (79-й рейс научно-исследовательского судна “Академик Мстислав Келдыш”) // Океанология. 2020. Т. 60. № 5. С. 823–825. https://doi.org/10.31857/S0030157420050172

  10. Морозов Е.Г., Фрей Д.И., Полухин А.А. и др. Мезомасштабная изменчивость океана в северной части моря Уэдделла // Океанология. 2020. Т. 60. № 5. С. 663–679.https://doi.org/10.31857/S0030157420050184

  11. Спиридонов В.А., Залота А.К., Яковенко В.А., Горбатенко К.М. Состав популяции и транспорт молоди антарктического криля в районе бассейна Пауэлла (северо-западная часть моряУэдделла) в январе 2020 г. // Труды ВНИРО. 2020. Т. 18. С. 33–51.

  12. An Atlas of Internal Solitary-like Waves and Their Properties. 2nd Edition. 2004. https://www.internalwaveatlas.com/Atlas2_index.html (Дата обращения: 01.09.2022 г.). (13/1)

  13. Bukatov A.A., Solovei N.M., Pavlenko E.A. Free short-period internal waves in the Arctic Seas of Russia // Physical Oceanography, [e-journal. 2021] 28(6). P. 599– 611. https://doi.org/10.22449/1573-160X-2021-6-599-611

  14. Fahrbach E., Beckmann A. Weddell Sea Circulation // Encyclopedia of Ocean Sciences, 1st edition. Elsevier Ltd. 2001. V. 6. P. 3201–3209.

  15. Gill A.E.Circulation and bottom water production in the Weddell Sea // Deep-Sea Research. 1973. V. 20. № 2. P. 111–140.

  16. Eagles G., Livermore R.A. Opening history of Powell Basin, Antarctic Peninsula // Marine Geology. 2002. V. 185. P. 195–205.

  17. Klemas V. Remote sensing of ocean internal waves: An Overview // Journal of Coastal Research. 2012. V. 28(3). P. 540–546. https://doi.org/10.2112/JCOASTRES-D-11-00156.1

  18. Mueller R.D., Timmermann R. Weddell Sea Circulation // Encyclopedia of Ocean Sciences, 3rd Edition. 2018. P. 1–7. https://doi.org/10.1016/B978-0-12-409548-9.11631-8

  19. Special report on the ocean and cryosphere in a changing climate. https://www.ipcc.ch/srocc/ (дата обращения 01.10.2022).

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Океанология

Архивы выпусков Информация о журнале Отправить рукопись в журнал