Проблемы машиностроения и надежности машин, 2019, № 1, стр. 74-85

УПОРНЫЕ ПОДШИПНИКИ СКОЛЬЖЕНИЯ В ТУРБУЛЕНТНОМ РЕЖИМЕ ТРЕНИЯ С УЧЕТОМ РЕОЛОГИЧЕСКИХ СВОЙСТВ ВЯЗКОУПРУГОГО СМАЗОЧНОГО МАТЕРИАЛА

И. В. Колесников¹, Е. С. Новиков^1, *

¹ Ростовский государственный университет путей сообщения
г. Ростов-на-Дону, Россия

Поступила в редакцию 08.10.2018

DOI: 10.1134/S0235711919010024

Аннотация

На основе представлений о турбулентном течении вязкоупругого смазочного материала, рассмотрена двухкомпонентная система смазки, состоящая из минерального масла и вязкоупругого смазочного материала, являющегося расплавом легкоплавких металлов. Представлены результаты исследований трибологических характеристик – силы трения и несущей способности узлов трения, с учетом температурной зависимости вязкости и модуля сдвига расплавленного слоя. Рассматриваются пути улучшения свойств смазок введением в них присадок и наполнителей.

При передаче больших мощностей червячными редукторами, шлицевыми соединениями трибосистем, в которых используется в качестве смазочного материала минеральное масло, возникают трудности из-за его недостатка, которое необходимо для предотвращений схватывания при повышении температуры рабочих поверхностей. Чтобы избежать подобных ситуаций, а также при высоких температурах и напряжениях для подшипников скольжения предлагается использовать в качестве дополнительного смазочного материала расплав легкоплавких металлов.

В качестве твердого смазочного материала (ТСМ) применяются свинец, олово, индий, литий, кадмий и другие материалы и сплавы. В настоящих исследованиях для стального трибосопряжения в качестве твердой смазки было использовано олово (температура плавления Т_пл = 232°С).

Известны различные технологии металлизации поверхности трибосопряжения, где особого внимания заслуживает диффузная металлизация по своей экономичности и простоте с применением стандартного оборудования [1]. Используя эту технологию, на поверхности изделий можно получить однокомпонентные и многокомпонентные диффузионные покрытия на основе разных металлических элементов.

Смазывание расплавом изучалось во многих прикладных задачах, например, в процессах формоизменения и резания металлов [2–13]. Разработке расчетной модели радиальных и упорных подшипников скольжения с учетом как реологических свойств вязкоупругого, микрополярного смазочного материала, так и зависимости вязкости смазки от давления и расплава легкоплавкого покрытия посвящен ряд работ [14–20].

Однако, отсутствие исследований по определению трибологических характеристик зависимости вязкости смазочного материала и модуля сдвига для расплава от температуры снижает эффективность использования этих материалов в тяжелонагруженных узлах трения.

В настоящей работе решение задачи по определению триботехнических характеристик (несущей способности и силы трения) подшипника приводится для случая, когда смазка обладает вязкоупругими свойствами, с учетом зависимости вязкости смазочного материала и модуля сдвига от температуры, а также расплава легкоплавкого покрытия.

Важно не только определить трибологические параметры смазочного материала, обусловленного расплавом, и получить высококачественные смазки с добавками, но и добиться, чтобы эти смазки были устойчивы и обладали стабильными свойствами в широком температурном интервале. Для этого решение задачи было найдено на основе системы уравнений, описывающих движения несжимаемого жидкого вязкоупругого смазочного материала для случая “тонкого слоя” с учетом зависимости вязкости жидкого смазочного материала и модуля сдвига от температуры, а также уравнения неразрывности и выражения для скорости диссипации механической энергии при определении функции, обусловленной расплавом. Наиболее перспективным направлением подбора наполнителей в смазку является применение природных минералов, диспергированных до коллоидного состояния. Данными минералами выступают силикаты, которые совместимы с базовыми маслами и способны образовывать смазочную пленку на поверхности трибосопряжения [22].

Постановка задачи. Рассматриваем упорный подшипник, состоящий из системы “ползун-направляющая”. Делаем ряд предположений: 1) ползун неподвижен; 2) направляющая, выполненная из материала с низкой температурой плавления, движется в сторону сужения зазора со скоростью $u{\text{*}}$; 3) между поверхностью ползуна и направляющей слой смазочного материала, обладающий вязкоупругими свойствами (рис. 1).

Рис. 1.

Рабочая схема.

В декартовой системе координат $xoy$ уравнение контура ползуна и расплавленной поверхности направляющей можно записать в виде

(1)

$y{\text{'}} = {{h}_{0}} + х {\text{'}}\operatorname{tg} \alpha *,\quad y{\text{'}} = - \Phi (x'),$

где ${{h}_{0}}$ – толщина смазочной пленки в начальном сечении; $\Phi \left( {x{\text{'}}} \right)$ – толщина расплавленной пленки в начальном сечении; $\alpha {\text{*}}$ – угол наклона линейного контура ползуна к оси $О х {\text{'}}$.

Предполагаем, что зависимость вязкости и модуля сдвига от давления и температуры выражается формулами $\mu {\text{'}} = {{\mu }_{0}}{{e}^{{ - \alpha {\text{'(}}Т {\text{'}} - {{{\tilde {Т }}}_{0}}{\text{)}}}}}$, $G{\text{'}} = {{G}_{0}}{{e}^{{ - \alpha {\text{'}}(Т {\text{'}} - {{{\tilde {Т }}}_{0}})}}}$, где $\mu {\text{'}}$ – коэффициент динамической вязкости смазочного материала; $G{\text{'}}$ – модуль сдвига; ${{\mu }_{0}}$ – характерная вязкость ньютоновского смазочного материала; ${{G}_{0}}$ – характерное значение модуля сдвига; $\alpha {\text{'}}$ – экспериментальная постоянная величина; $Т {\text{'}} = Т \left( {х {\text{'}}} \right)$ – температура в смазочном слое, ${{\tilde {Т }}_{0}}$ – начальная температура.

При формировании аналитического решения задачи делаем следующие предположения: Давление $р $ постоянно по толщине смазочной пленки, заданной уравнениями (1); жидкая среда является вязкой несжимаемой жидкостью; все тепло, выделяющееся в смазочной пленке, идет на плавление поверхности материала направляющей; влияние турбулентности можно отразить с помощью коэффициента $j > 1$, на который следует умножить вязкость, чтобы получить величину эффективной вязкости (предполагаем, что коэффициент $j$ можно выразить в виде функции числа Рейнольдса j = = $0.0139{{\operatorname{Re} }^{{0.657}}}$, где $\operatorname{Re} = {\rho }u{\text{*}}h_{0}^{2}{\text{/}}{{{\mu }}_{0}}l$ – число Рейнольдса, ${\rho }$ – плотность, $u{\text{*}}$ – скорость движения).

Исходные уравнения и граничные условия. В качестве исходных уравнений рассмотрим систему безразмерных уравнений движения смазочного материала, обладающего вязкоупругими свойствами для случая “тонкого слоя”, уравнения неразрывности и формулу скорости диссипации энергии, для определения функции $\Phi \left( x \right)$, обусловленной расправленной направляющей

(2)

$\frac{{{{\partial }^{2}}\text{v}}}{{\partial {{y}^{2}}}} = \frac{1}{{j\mu (x)}}\frac{{dp}}{{dx}} + \frac{\beta }{{j\mu (x)}}\frac{{{{d}^{2}}p}}{{d{{x}^{2}}}},\quad \frac{{\partial u}}{{\partial y}} + \frac{{\partial \text{v}}}{{\partial x}} = 0,\quad - {\kern 1pt} \frac{1}{{j\mu (x)}}\frac{{d\Phi (x)}}{{dx}} = - K{{\int\limits_{ - \Phi \left( x \right)}^{h\left( x \right)} {\left( {\frac{{\partial \text{v}}}{{\partial y}}} \right)} }^{2}}dy,$

где $u$, $\text{v}$ – компоненты вектора скорости смазочной среды; $\beta = {{\mu }_{0}}u{\text{*/}}Glh$ – число Дебора; $p$ – гидродинамическое давление в смазочном слое; $\mu $ – коэффициент динамической вязкости; $K = 2{{\mu }_{0}}u{\text{*}}l{\text{/}}h_{0}^{2}L$ – параметр, характеризующий скорость диссипации механической энергии; $L$ – удельная теплота плавления на единицу объема.

Систему уравнений (2) решаем совместно с граничными условиями

$\begin{gathered} u = 0,\quad \text{v} = 0\quad {\text{п р и }}\quad y = 1 + \eta х = h\left( x \right);\quad u = 0, \\ \text{v} = - 1\quad {\text{п р и }}\quad y = - \Phi \left( x \right);\quad p\left( 0 \right) = p\left( 1 \right) = \frac{{{{p}_{a}}}}{{p{\text{*}}}},\quad {\text{г д е }}\quad \eta = \frac{{l\operatorname{tg} \alpha {\text{*}}}}{{{{h}_{0}}}}. \\ \end{gathered} $

Допускаем, что смазочный материал поступает в подшипник при отсутствии упругой компоненты деформации. Тогда характеристику особого состояния смазочной среды запишем следующим образом:

(3)

$\frac{{dc}}{{dx}} = 0,\quad \frac{{{{d}^{2}}p}}{{d{{x}^{2}}}} = 0\quad {\text{п р и }}\quad x = 0;\quad \Phi (x) = {{\tilde {g}}_{0}} = K{{g}_{0}} = 0\quad {\text{п р и }}\quad x = 0,$

где $c$ – напряжения, обусловленные упругостью смазки.

Переход к безразмерным переменным реализуется по формулам

$u{\text{'}} = u{\text{*}}u,\quad \text{v}{\text{'}} = u{\text{*}}\varepsilon \text{v},\quad x{\text{'}} = lx,\quad y{\text{'}} = {{h}_{0}}y,\quad Т {\text{'}} = Т {\text{*}}Т ,\quad T{\text{*}} = \frac{{{{\mu }_{0}}u{{{\text{*}}}^{2}}l{{h}^{2}}}}{{I\lambda }}{\text{,}}\quad {\alpha } = {\alpha '}T{\text{*,}}$

${\varepsilon } = \frac{{{{h}_{0}}}}{l}{\text{,}}\quad {\mu '} = {{{\mu }}_{0}}{\mu ,}\quad G{\text{'}} = {{G}_{0}}{\text{G,}}\quad C{\text{'}} = C{\text{*}}C,\quad C* = \frac{{{{{\mu }}_{0}}u{\text{*}}}}{{{{h}_{0}}}},\quad p* = \frac{{{{{\mu }}_{0}}u{\text{*}}l}}{{h_{0}^{2}}}.$

Функцию $\Phi \left( х \right)$ ищем в виде $\Phi \left( х \right)$ = $ - K{{\Phi }_{1}}$ – ${{K}^{2}}{{\Phi }_{2}}$ – – ${{K}^{3}}{{\Phi }_{3}} - \ldots = H$.

Граничные условия для безразмерных компонентов скорости u и $\text{v}$ на контуре $y = 0 - \Phi (x)$ можно записать в виде

$\text{v}\left( {0 - H\left( х \right)} \right) = \text{v}\left( 0 \right) - {{\left. {\left( {\frac{{\partial \text{v}}}{{\partial y}}} \right)} \right|}_{{y = 0}}}H\left( х \right) - {{\left. {\left( {\frac{{{{\partial }^{2}}\text{v}}}{{\partial {{y}^{2}}}}} \right)} \right|}_{{y = 0}}}{{H}^{2}}\left( х \right) - \ldots = - 1,$

$u\left( {0 - H\left( x \right)} \right) = u\left( 0 \right) - {{\left. {\left( {\frac{{\partial u}}{{\partial y}}} \right)} \right|}_{{y = 0}}}H\left( х \right) - {{\left. {\left( {\frac{{{{\partial }^{2}}u}}{{\partial {{y}^{2}}}}} \right)} \right|}_{{y = 0}}}{{H}^{2}}\left( х \right) - \ldots = 0.$

Ищем асимптотическое решение системы уравнений (2), учитывая (3), в виде

$\text{v} = {{\text{v}}_{0}}(x,y) + K{{\text{v}}_{1}}(x,y) + {{K}^{2}}{{\text{v}}_{2}}(x,y) + \ldots ,\quad u = {{u}_{0}}(x,y) + K{{u}_{1}}(x,y) + {{K}^{2}}{{u}_{2}}(x,y) + \ldots ,$

(4)

$\Phi (x) = - K{{\Phi }_{1}}(x) - {{K}^{2}}{{\Phi }_{2}}(x) - {{K}^{3}}{{\Phi }_{3}}(x) - \ldots ,$

$T = {{T}_{0}}(x) + K{{T}_{1}}(x) + {{K}^{2}}{{T}_{2}}(x) + {{K}^{3}}{{T}_{3}}(x) \ldots ,\quad {\mu } = {{{\mu }}_{0}}(x) + K{{{\mu }}_{1}}(x) + {{K}^{2}}{{{\mu }}_{2}}(x) + {{K}^{3}}{{{\mu }}_{3}}(x) \ldots .$

Подставляем (4) в систему (2) и учитывая (3), получаем следующие уравнения:

для нулевого приближения

(5)

$\frac{{{{\partial }^{2}}{{\text{v}}_{0}}}}{{\partial {{y}^{2}}}} = \frac{1}{{{\text{j}}{{{\mu }}_{0}}\left( х \right)}}\frac{{d{{р }_{0}}}}{{dx}} + \frac{{\beta }}{{{\text{j}}{{{\mu }}_{0}}\left( х \right)}}\frac{{{{d}^{2}}{{р }_{0}}}}{{d{{x}^{2}}}},\quad \frac{{\partial {{\text{v}}_{0}}}}{{\partial x}} + \frac{{\partial {{u}_{0}}}}{{\partial y}} = 0$

с граничными условиями

(6)

$\begin{gathered} {{\text{v}}_{0}} = 0,\quad {{u}_{0}} = 0\quad {\text{п р и }}\quad y = 1 + \eta x;\quad {{\text{v}}_{0}} = - 1,\quad {{u}_{0}} = 0\quad {\text{п р и }}\quad y = 0; \\ {\text{C}}_{0}^{'}(0) = 0;\quad р _{0}^{{''}}(0) = 0;\quad {{р }_{0}}(0) = {{р }_{0}}(1) = \frac{{{{p}_{a}}}}{{p{\text{*}}}};\quad K{{\Phi }_{0}}(0) = K{{g}_{0}} = 0; \\ \end{gathered} $

для первого приближения с точностью до членов $О (K{/\mu }_{0}^{2})$

(7)

$\frac{{{{\partial }^{2}}{{\text{v}}_{1}}}}{{\partial {{y}^{2}}}} = \frac{1}{{{\text{j}}{{{\mu }}_{0}}(x)}}\left( {\frac{{d{{р }_{1}}}}{{dx}} + \beta \frac{{{{d}^{2}}{{р }_{1}}}}{{d{{x}^{2}}}}} \right),\quad \frac{{\partial {{\text{v}}_{1}}}}{{\partial x}} + \frac{{\partial {{u}_{1}}}}{{\partial y}} = 0,\quad \frac{1}{{{\text{j}}{{{\mu }}_{0}}(x)}}\frac{{d{{\Phi }_{1}}(x)}}{{dx}} = K\int\limits_0^{1 + \eta x} {{{{\left( {\frac{{\partial {{\text{v}}_{0}}}}{{\partial y}}} \right)}}^{2}}dy} $

с граничными условиями

(8)

$\begin{gathered} {{\text{v}}_{1}} = {{\left. {\left( {\frac{{\partial {{\text{v}}_{0}}}}{{\partial y}}} \right)} \right|}_{{y = 0}}}{{\Phi }_{1}}(x);\quad {{u}_{1}} = {{\left. {\left( {\frac{{\partial {{u}_{0}}}}{{\partial y}}} \right)} \right|}_{{y = 0}}}{{\Phi }_{1}}(x); \\ {{\text{v}}_{1}} = 0,\quad {{u}_{1}} = 0\quad {\text{п р и }}\quad h(x) = 1 + \eta x; \\ C_{0}^{'}(0) = 0;\quad р _{1}^{{''}}(0) = 0;\quad {{р }_{1}}(0) = {{р }_{1}}(1) = 0;\quad K{{\Phi }_{1}}(0) = K\tilde {\tilde {\alpha }}*;\quad {{\Phi }_{1}}(0) = \tilde {\tilde {\alpha }}{\text{*}}. \\ \end{gathered} $

Точное автомодельное решение задачи для нулевого приближения ищем по методу Ахвердиева К.С. [21]

(9)

$\begin{gathered} {{u}_{0}} = - \frac{{\partial {{\psi }_{0}}}}{{\partial x}} + {{U}_{0}}(x,y),\quad {{\text{v}}_{0}} = \frac{{\partial {{\psi }_{0}}}}{{\partial y}} + {{V}_{0}}(x,y),\quad {{\psi }_{0}}(x,y) = {{{\tilde {\psi }}}_{0}}\left( \xi \right), \\ \xi = \frac{y}{{h(x)}},\quad {{V}_{0}}(x,y) = \tilde {v}\left( \xi \right),\quad {{U}_{0}}(x,y) = - {{{\tilde {u}}}_{0}}\left( \xi \right) \cdot h{\text{'}}(x). \\ \end{gathered} $

Подставляя (9) в систему уравнений (5), (6), получаем систему дифференциальных уравнений

(10)

$\begin{gathered} \tilde {\psi }_{0}^{{'''}} = {{{\tilde {С }}}_{2}},\quad \tilde {v}_{0}^{{''}} = {{{\tilde {C}}}_{2}},\quad \tilde {u}_{0}^{'} + \xi \tilde {v}_{0}^{'} = 0; \\ \frac{\beta }{{{\text{j}}{{{\mu }}_{0}}(x)}}\frac{{{{d}^{2}}{{р }_{0}}}}{{d{{x}^{2}}}} + \frac{1}{{{\text{j}}{{{\mu }}_{0}}(x)}}\frac{{d{{р }_{0}}}}{{dx}} = \frac{{{{{\tilde {C}}}_{1}}}}{{{{h}^{2}}(x)}} + \frac{{{{{\tilde {C}}}_{2}}}}{{{{h}^{3}}(x)}} \\ \end{gathered} $

и граничные условия

$\begin{gathered} \tilde {\psi }_{0}^{'}\left( 0 \right) = 0,\quad \tilde {\psi }{{_{{}}^{'}}_{0}}\left( 1 \right) = 0;\quad {{{\tilde {u}}}_{0}}\left( 1 \right) = 0,\quad {{{\tilde {v}}}_{0}}\left( 1 \right) = 0, \\ {{{\tilde {u}}}_{0}}\left( 0 \right) = 0,\quad {{{\tilde {v}}}_{0}}\left( 0 \right) = - 1,\quad \int\limits_0^1 {{{{\tilde {v}}}_{0}}\left( \xi \right)} d\xi = 0,\quad {{р }_{0}}\left( 0 \right) = {{р }_{0}}\left( 1 \right) = \frac{{{{p}_{a}}}}{{p{\text{*}}}}. \\ \end{gathered} $

Проинтегрируем (10) и получим

(11)

$\tilde {\psi }_{0}^{'}\left( \xi \right) = \frac{{{{{\tilde {С }}}_{2}}}}{2}\left( {{{\xi }^{2}} - \xi } \right),\quad {{\tilde {v}}_{0}}\left( {\xi } \right) = {{\tilde {С }}_{1}}\frac{{{{{\xi }}^{{\text{2}}}}}}{2} + \left( {1 - \frac{{{{{\tilde {C}}}_{1}}}}{2}} \right){\xi } - 1,\quad {{\tilde {С }}_{1}} = 6.$

Из условий ${{р }_{0}}\left( 0 \right) = {{р }_{0}}\left( 1 \right) = \frac{{{{p}_{a}}}}{{p{\text{*}}}}$ и $р _{0}^{{''}}\left( 0 \right) = 0$ решая уравнение

$\frac{\beta }{{{\text{j}}{{{\mu }}_{0}}\left( х \right)}}\frac{{{{d}^{2}}{{р }_{0}}}}{{d{{x}^{2}}}} + \frac{1}{{{\text{j}}{{{\mu }}_{0}}\left( х \right)}}\frac{{d{{р }_{0}}}}{{dx}} = \frac{{{{{\tilde {C}}}_{1}}}}{{{{h}^{2}}\left( x \right)}} + \frac{{{{{\tilde {C}}}_{2}}}}{{{{h}^{3}}\left( x \right)}}$

${\text{д л я }}\;{{\tilde {C}}_{2}}\;{\text{п о л у ч и м }}\quad {{\tilde {C}}_{2}} = \frac{{6\eta - 12\eta \beta - 6 - 12\eta {{\beta }^{2}}\left( {{{е }^{{ - \frac{1}{\beta }}}} - 1} \right)}}{{1 + 3\eta {{\beta }^{2}} - \frac{3}{2}\eta - 3\eta {{\beta }^{2}}\left( {{{е }^{{ - \frac{1}{\beta }}}} - 1} \right)}}.$

Гидродинамическое давление в смазочном слое определяем из уравнения

Для этого сначала необходимо найти ${{{\mu }}_{0}}\left( x \right)$. Продифференцировав ${{{\mu }}_{0}}\left( x \right)$ = ${{e}^{{ - \alpha \left( {Т - \frac{{{{{\tilde {T}}}_{0}}}}{{T{\text{*}}}}} \right)}}}$ получим

(12)

$\frac{{d{{\mu }_{0}}\left( x \right)}}{{dх }} = {{\mu }_{0}}\left( х \right)\left( { - \alpha \frac{{d{{T}_{0}}}}{{dх }}} \right).$

Для определения $d{{T}_{0}}{\text{/}}dх $ используем формулу для скорости диссипации энергии

(13)

$\frac{{d{{T}_{0}}}}{{dх }} = - \frac{{24{{\mu }_{0}}{{\mu }_{0}}\left( x \right)u{\text{*}}lh\left( x \right)}}{{T{\text{*}}{{c}_{p}}h_{0}^{2}{{{\tilde {C}}}_{2}}}}\int\limits_0^1 {{{{\left( {\frac{{\tilde {\psi }{{{_{0}^{{''}}}}_{{}}}\left( \xi \right)}}{{{{h}^{2}}\left( x \right)}} + \frac{{\tilde {v}{{{_{{}}^{'}}}_{0}}\left( \xi \right)}}{{h\left( x \right)}}} \right)}}^{2}}d\xi .} $

Подставляя (13) в (12) и сделав ряд преобразований, получим

(14)

$\frac{1}{{\mu _{0}^{2}\left( x \right)}}\frac{{d{{\mu }_{0}}\left( х \right)}}{{dx}} = \frac{{24{{\mu }_{0}}u{\text{*}}l\alpha h\left( x \right)}}{{T{\text{*}}{{c}_{p}}h_{0}^{2}{{{\tilde {C}}}_{2}}}}\int\limits_0^1 {{{{\left( {\frac{{\tilde {\psi }_{0}^{{''}}\left( \xi \right)}}{{{{h}^{2}}\left( x \right)}} + \frac{{\tilde {v}_{0}^{'}\left( \xi \right)}}{{h\left( x \right)}}} \right)}}^{2}}d\xi ,} $

где ${{c}_{p}}$ – теплоемкость при постоянном давлении.

Интегрируя (14), получим

$\frac{1}{{{{\mu }_{0}}(x)}} = - \tilde {D}[{{\Delta }_{1}}{{J}_{3}}(x) + {{\Delta }_{2}}{{J}_{2}}(x) + {{\Delta }_{3}}{{J}_{1}}(x)],$

где

$\tilde {D} = \frac{{24{{\mu }_{0}}\alpha u{\text{*}}l}}{{T{\text{*}}{{c}_{p}}h_{0}^{2}{{{\tilde {C}}}_{2}}}},\quad {{\Delta }_{1}} = \int\limits_0^1 {{{{\left( {\tilde {\psi }{\text{''}}\left( \xi \right)} \right)}}^{2}}} d\xi = \frac{{\tilde {C}_{2}^{2}}}{{12}},$

${{\Delta }_{2}} = 2\int\limits_0^1 {\left( {\tilde {\psi }{\text{''}}\left( \xi \right) \cdot \tilde {v}{\text{'}}\left( \xi \right)} \right)} d\xi = \frac{1}{6}{{\tilde {C}}_{1}}{{\tilde {C}}_{2}},\quad {{\Delta }_{3}} = \int\limits_0^1 {{{{\left( {\tilde {v}{\text{'}}\left( \xi \right)} \right)}}^{2}}} d\xi = 4,\quad {{J}_{k}}\left( x \right) = \int\limits_0^x {\frac{{dx}}{{{{h}^{k}}\left( x \right)}}.} $

Функцию ${{\mu }_{0}}\left( x \right)$ заменим ее усредненным интегральным значением

${{\tilde {\mu }}_{0}} = \int\limits_0^1 {{{\mu }_{0}}(x)dx} = \int\limits_0^1 {\frac{{dx}}{{ - \tilde {D}[{{\Delta }_{1}}{{J}_{3}}(x) + {{\Delta }_{2}}{{J}_{2}}(x) + {{\Delta }_{3}}{{J}_{1}}(x)]}}.} $

С точностью до $О ({{{\eta }}^{2}})$ для $\tilde {\mu }$ получим следующее выражение:

${{\tilde {\mu }}_{0}} = 1 + D\alpha \left( {\frac{{235}}{8}\eta {{\beta }^{2}}\left( {{{е }^{{ - \frac{1}{\beta }}}} - 1} \right) + \frac{{631}}{{24}}\eta + \frac{{49}}{4} - \frac{{47}}{4}\eta \beta } \right),\quad {\text{г д е }}\quad D = \frac{{24{{\mu }_{0}}u{\text{*}}l}}{{T{\text{*}}{{c}_{p}}h_{0}^{2}}}.$

Тогда

(15)

$\begin{gathered} {{p}_{0}} = j{{{\tilde {\mu }}}_{0}}\left[ { - 15\eta {{\beta }^{2}} + \eta {{\beta }^{2}}{{е }^{{ - \frac{x}{\beta }}}} + 6\left( {х + 2\eta \left( {\beta - \frac{{{{х }^{2}}}}{2}} \right)} \right) + } \right. \\ \left. { + \;15\eta х - 6х + 6\eta \beta х - 15\eta {{\beta }^{2}}х \left( {{{е }^{{ - \frac{1}{\beta }}}} - 1} \right) - 18\eta \left( {\beta х - \frac{{{{x}^{2}}}}{2}} \right)} \right] + \frac{{{{p}_{a}}}}{{p{\text{*}}}}. \\ \end{gathered} $

Для определения ${{\Phi }_{1}}\left( x \right)$ с учетом уравнения (11), придем к уравнению

(16)

$\frac{{d{{\Phi }_{1}}}}{{dx}} = j{{\tilde {\mu }}_{0}}h\left( x \right){{\int\limits_0^1 {\left( {\frac{{\psi _{0}^{{''}}\left( \xi \right)}}{{{{h}^{2}}\left( x \right)}} + \frac{{\tilde {v}_{0}^{'}\left( \xi \right)}}{{h\left( x \right)}}} \right)} }^{2}}d\xi .$

Интегрируем уравнение (16) и получаем

(17)

${{\Phi }_{1}}\left( x \right) = j{{{\tilde {\mu }}}_{0}}\left[ {\int\limits_0^x {\frac{{{{\Delta }_{1}}dx}}{{{{h}^{3}}\left( x \right)}}} + \int\limits_0^x {\frac{{{{\Delta }_{2}}dx}}{{{{h}^{2}}\left( x \right)}}} + \int\limits_0^x {\frac{{{{\Delta }_{3}}dx}}{{h\left( x \right)}}} } \right].$

Решая уравнения c учетом $K{{\Phi }_{1}}\left( 0 \right) = K\tilde {\tilde {\alpha }}{\text{*}}$, получим

${{\Phi }_{1}}\left( х \right) = j{{\tilde {\mu }}_{0}}\left[ {\left( {x - \frac{3}{2}{\eta }{{x}^{2}}} \right)\frac{{\tilde {С }_{2}^{2}}}{{12}} + {{{\tilde {С }}}_{2}}\left( {х - {\eta }{{x}^{2}}} \right) + 4\left( {х - \frac{{\eta }}{2}{{x}^{2}}} \right) + \tilde {\tilde {\alpha }}{\text{*}}} \right].$

Точное решение по методу Ахвердиева К.С. для первого приближения ищем в виде [21]

(18)

$\begin{gathered} {{u}_{1}} = - \frac{{\partial {{\psi }_{1}}}}{{\partial x}} + {{U}_{1}}(x,y),\quad {{\text{v}}_{1}} = \frac{{\partial {{\psi }_{1}}}}{{\partial y}} + {{V}_{1}}(x,y),\quad {{\psi }_{1}}(x,y) = {{{\tilde {\psi }}}_{1}}\left( \xi \right), \\ \xi = \frac{y}{{h(x)}},\quad {{V}_{1}}(x,y) = \tilde {v}\left( \xi \right),\quad {{U}_{1}}(x,y) = - {{{\tilde {u}}}_{1}}\left( \xi \right) \cdot h{\text{'}}{\kern 1pt} (x). \\ \end{gathered} $

Подставляем (18) в систему (7), (8), получаем систему дифференциальных уравнений

$\tilde {\psi }{{_{1}^{{'''}}}_{1}}\left( \xi \right) = {{\tilde {\tilde {С }}}_{2}},\quad \tilde {v}_{1}^{{''}} = {{\tilde {\tilde {С }}}_{1}},\quad \tilde {u}_{1}^{'} + \xi \tilde {v}_{1}^{'} = 0,$

$\frac{\beta }{{j{{\mu }_{1}}\left( х \right)}}\frac{{{{d}^{2}}{{р }_{1}}}}{{d{{x}^{2}}}} + \frac{1}{{j{{\mu }_{1}}\left( х \right)}}\frac{{d{{р }_{1}}}}{{dx}} = \frac{{{{{\tilde {\tilde {C}}}}_{1}}}}{{{{h}^{2}}\left( x \right)}} + \frac{{{{{\tilde {\tilde {C}}}}_{2}}}}{{{{h}^{3}}\left( x \right)}},$

и граничные условия

$\begin{gathered} \tilde {\psi }_{1}^{'}\left( 0 \right) = 0;\quad \tilde {\psi }_{1}^{'}\left( 1 \right) = 0;\quad {{{\tilde {u}}}_{1}}\left( 1 \right) = 0;\quad {{{\tilde {v}}}_{1}}\left( 1 \right) = 0; \\ {{{\tilde {v}}}_{1}}\left( 0 \right) = M;\quad {{{\tilde {u}}}_{1}}\left( 0 \right) = 0;\quad \int\limits_0^1 {{{{\tilde {v}}}_{1}}\left( \xi \right)} d\xi = 0;\quad {{р }_{1}}\left( 0 \right) = {{р }_{1}}\left( 1 \right) = 0. \\ \end{gathered} $

Интегрируя получаем

$\tilde {\psi }{{_{1}^{'}}_{1}}\left( \xi \right) = \frac{{{{{\tilde {\tilde {С }}}}_{2}}}}{2}\left( {{{\xi }^{2}} - \xi } \right),\quad {{\tilde {v}}_{1}}\left( {\xi } \right) = {{\tilde {\tilde {С }}}_{1}}\frac{{{{{\xi }}^{{\text{2}}}}}}{2} - \left( {\frac{{{{{\tilde {\tilde {C}}}}_{1}}}}{2} + M} \right){\xi } + M,\quad {{\tilde {\tilde {С }}}_{1}} = 6M,$

где

$\begin{gathered} M = \mathop {\sup }\limits_{x \in \left[ {0;1} \right]} {{\left. {\left( {\frac{{\partial {{\text{v}}_{0}}}}{{\partial y}}} \right)} \right|}_{{y = 0}}}{{\Phi }_{1}}\left( x \right) = \\ = \mathop {\sup }\limits_{x \in \left[ {0;1} \right]} \left| {\,\left[ {1 - {\eta }x + 6{\eta }x - \frac{{15}}{2}{\eta } - {6\eta \beta + }\frac{{15}}{2}{\eta }{{{\beta }}^{2}}\left( {{{e}^{{ - \frac{1}{\beta }}}} - 1} \right) + 9{\eta }\left( {{\beta } - х } \right)} \right]} \right. \times \\ \times \;\left. {{\text{j}}{{{{\tilde {\mu }}}}_{0}}\left[ {\left( {x - \frac{3}{2}{\eta }{{x}^{2}}} \right)\frac{{\tilde {C}_{2}^{2}}}{{12}} + {{{\tilde {C}}}_{2}}(x - {\eta }{{x}^{2}}) + 4\left( {x - \frac{1}{2}{\eta }{{x}^{2}}} \right) + {\tilde {\alpha }}} \right]\,} \right|. \\ \end{gathered} $

Из условия ${{р }_{1}}\left( 0 \right) = {{р }_{1}}\left( 1 \right) = 0$ для ${{\tilde {\tilde {С }}}_{2}}$ получим

${{\tilde {\tilde {С }}}_{2}} = М \left( {15\eta - 6 + 6\eta \beta } \right) - 15\eta {{\beta }^{2}}\left( {{{е }^{{ - \frac{1}{\beta }}}} - 1} \right).$

Для определения значения ${{\tilde {\tilde {C}}}_{2}}$ и гидродинамического давления ${{р }_{1}}$ необходимо найти ${{\mu }_{1}}\left( х \right)$. Продифференцировав ${{\mu }_{1}}(x)$ = ${{e}^{{ - \alpha \left( {{{T}_{1}} - \frac{{{{{\tilde {Т }}}_{0}}}}{{Т {\text{*}}}}} \right)}}}$ по х, получим

(19)

$\frac{{d{{\mu }_{1}}\left( х \right)}}{{dx}} = - \alpha \left( {{{\mu }_{0}}\left( х \right)\frac{{d{{T}_{1}}}}{{dx}} + {{\mu }_{1}}\left( х \right)\frac{{d{{T}_{0}}}}{{dx}}} \right).$

Для определения $d{{T}_{1}}{\text{/}}dx$ применяем формулу для скорости диссипации энергии

(20)

$\frac{{d{{T}_{1}}}}{{dх }} = - \frac{{48{{\mu }_{0}}{{\mu }_{1}}\left( х \right)u{\text{*}}lh\left( x \right)}}{{T{\text{*}}{{c}_{p}}h_{0}^{2}{{{\tilde {\tilde {C}}}}_{2}}}}\int\limits_0^1 {\left( {\frac{{\tilde {\psi }_{0}^{{''}}\left( \xi \right)}}{{{{h}^{2}}\left( x \right)}} + \frac{{\tilde {v}_{0}^{'}\left( \xi \right)}}{{h\left( x \right)}}} \right)\left( {\frac{{\tilde {\psi }{{{_{{}}^{{''}}}}_{1}}\left( \xi \right)}}{{{{h}^{2}}\left( x \right)}} + \frac{{\tilde {v}_{1}^{'}\left( \xi \right)}}{{h\left( x \right)}}} \right)d\xi .} $

Подставляя (13) и (20) в (19) и сделав ряд преобразований, получим

(21)

$\begin{gathered} \frac{1}{{{{{\tilde {\mu }}}_{0}}{{\mu }_{1}}(x)}}\frac{{d{{\mu }_{1}}(x)}}{{dх }} = \frac{{48{{\mu }_{0}}u{\text{*}}l\alpha }}{{T{\text{*}}{{c}_{p}}h_{0}^{2}{{{\tilde {\tilde {C}}}}_{2}}}}\left( {\frac{{{{{\tilde {\Delta }}}_{1}}}}{{{{h}^{3}}(x)}} + \frac{{{{{\tilde {\Delta }}}_{2}}}}{{{{h}^{2}}(x)}} + \frac{{{{{\tilde {\Delta }}}_{3}}}}{{{{h}^{2}}(x)}} + \frac{{{{{\tilde {\Delta }}}_{4}}}}{{h(x)}}} \right) + \\ + \;\frac{{24{{\mu }_{0}}u{\text{*}}l\alpha }}{{T{\text{*}}{{c}_{p}}h_{0}^{2}{{{\tilde {C}}}_{2}}}}\left( {\frac{{{{\Delta }_{1}}}}{{{{h}^{3}}(x)}} + \frac{{{{\Delta }_{2}}}}{{{{h}^{2}}(x)}} + \frac{{{{\Delta }_{3}}}}{{h(x)}}} \right), \\ \end{gathered} $

где

${{\tilde {\Delta }}_{1}} = \int\limits_0^1 {\tilde {\psi }_{0}^{{''}}\left( \xi \right)\tilde {\psi }_{1}^{{''}}\left( \xi \right)} d\xi ;\quad {{\tilde {\Delta }}_{2}} = \int\limits_0^1 {\tilde {\psi }_{0}^{{''}}\left( \xi \right)\tilde {v}_{1}^{'}\left( \xi \right)} d\xi ;$

${{\tilde {\Delta }}_{3}} = \int\limits_0^1 {\tilde {\psi }_{1}^{{''}}\left( \xi \right)\tilde {v}_{0}^{'}\left( \xi \right)} d\xi ;\quad {{\tilde {\Delta }}_{4}} = \int\limits_0^1 {\tilde {v}_{0}^{'}\left( \xi \right)\tilde {v}_{1}^{'}\left( \xi \right)} d\xi .$

Проинтегрируем (21) и заменим ${{\mu }_{1}}\left( х \right)$ ее усредненным интегральным значением и получим

$\begin{gathered} \frac{1}{{{{{\tilde {\mu }}}_{0}}}}\ln \left| {{{{\tilde {\mu }}}_{1}}} \right| = \frac{{24{{\mu }_{0}}u{\text{*}}l\alpha }}{{T{\text{*}}{{c}_{p}}h_{0}^{2}}}\left[ {\frac{{{{{\tilde {C}}}_{2}}}}{6}\left( {\frac{1}{2} - \frac{\eta }{2}} \right) + \frac{{2M{{{\tilde {C}}}_{2}}}}{{{{{\tilde {\tilde {C}}}}_{2}}}}\left( {\frac{1}{2} - \frac{\eta }{3}} \right) - 1 + \frac{{2\eta }}{3} + \frac{{8M}}{{{{{\tilde {\tilde {C}}}}_{2}}}}\left( {\frac{1}{2} - \frac{\eta }{6}} \right)} \right. + \\ + \;\left. {\left( {\frac{{235}}{8}\eta {{\beta }^{2}}\left( {{{e}^{{ - \frac{1}{\beta }}}} - 1} \right) + \frac{{631}}{{24}}\eta + \frac{{49}}{4} - \frac{{47}}{4}\eta \beta } \right)} \right]. \\ \end{gathered} $

С точностью до членов $О ({{{\eta }}^{2}})$ для ${{\tilde {\mu }}_{1}}$, получим

$\begin{gathered} {{{\tilde {\mu }}}_{1}} = 1 - \exp \left[ { - \alpha {{{\tilde {\mu }}}_{0}}\left( {1 - D\left[ {\frac{{{{{\tilde {С }}}_{2}}}}{6}\left( {\frac{1}{2} - \frac{\eta }{2}} \right) + \frac{{2М {{{\tilde {С }}}_{2}}}}{{{{{\tilde {\tilde {С }}}}_{2}}}}\left( {\frac{1}{2} - \frac{\eta }{3}} \right) - 1{{ + }^{{^{{^{{{{{^{}}}^{}}}}}}}}}} \right.} \right.} \right. \\ + \;\frac{{2\eta }}{3} + \frac{{8M}}{{{{{\tilde {\tilde {С }}}}_{2}}}}\left( {\frac{1}{2} - \frac{\eta }{6}} \right) - \left. {\left. {\left. {\left( {\frac{{235}}{8}\eta {{\beta }^{2}}\left( {{{e}^{{ - \frac{1}{\beta }}}} - 1} \right) + \frac{{631}}{{24}}\eta + \frac{{49}}{4} - \frac{{47}}{4}\eta \beta } \right)} \right]} \right)} \right]. \\ \end{gathered} $

Тогда из условия ${{р }_{1}}\left( 0 \right) = {{р }_{1}}\left( 1 \right) = 0$ и $р _{1}^{{''}}\left( 0 \right) = 0$ получим

(22)

$\begin{gathered} {{р }_{1}} = j{{{\tilde {\mu }}}_{1}}\left[ {15\eta {{\beta }^{2}}\left( {{{e}^{{ - \frac{x}{\beta }}}} - 1} \right)\left( {1 - х } \right) + 6M\left( {x + 2{\eta }\left( {\beta - \frac{{{{x}^{2}}}}{2}} \right)} \right)} \right. + \\ \left. {^{{^{{^{{^{{^{{}}}}}}}}}} + \;М \left( {15\eta x - 6х + 6\eta \beta х - 18{\eta }\left( {\beta х - \frac{{{{x}^{2}}}}{2}} \right)} \right)} \right]. \\ \end{gathered} $

Результаты исследования и их обсуждения. Определим основные триботехнические характеристики подшипника. С учетом (5), (7), (15) и (22) для несущей способности и силы трения получим

$W = \frac{{{{{\mu }}_{{\text{0}}}}{{l}^{{\text{2}}}}u{\text{*}}}}{{h_{{\text{0}}}^{{\text{2}}}}}\int\limits_{\text{0}}^{\text{1}} {\left( {{{p}_{{\text{0}}}} - \frac{{{{p}_{a}}}}{{p{\text{*}}}} + K{{p}_{{\text{1}}}}} \right)} dx = $

$ = \;\frac{{{{{\mu }}_{{\text{0}}}}{{l}^{{\text{2}}}}u{\text{*}}j}}{{h_{{\text{0}}}^{{\text{2}}}}}\left\{ {{{{{\tilde {\mu }}}}_{{\text{0}}}}j\left[ { - {15\eta }{{{\beta }}^{{\text{2}}}} - {\eta \beta }\left( {{{e}^{{ - \frac{1}{\beta }}}} - {\text{1}}} \right) + {\text{6}}\left( {\frac{{\text{1}}}{{\text{2}}} + {2\beta }\left( {{\beta } - \frac{{\text{1}}}{{\text{6}}}} \right)} \right)} \right.} \right. + $

$ + \;\frac{{{\text{15}}}}{{\text{2}}}{\eta } - {\text{3}} + {3\eta \beta } - \left. {\frac{{{\text{15}}}}{{\text{2}}}{\eta }{{{\beta }}^{{\text{2}}}}\left( {{{e}^{{ - \frac{1}{\beta }}}} - {\text{1}}} \right) - {18\eta }\left( {\frac{{\beta }}{{\text{2}}} - \frac{{\text{1}}}{{\text{6}}}} \right)} \right] + $

(23)

$ + \;K{{\tilde {\mu }}_{{\text{1}}}}\left[ {{15\eta \beta }\left( {{{e}^{{ - \frac{1}{\beta }}}} - {\text{2}}} \right) - {15\eta }{{{\beta }}^{{\text{2}}}}\left( { - \frac{{\text{1}}}{{\beta }}{{e}^{{ - \frac{1}{\beta }}}} - \frac{{\text{1}}}{{{{{\beta }}^{{\text{2}}}}}}\left( {{{e}^{{ - \frac{1}{\beta }}}} - {\text{1}}} \right) + \frac{{\text{1}}}{{\text{2}}}} \right)} \right. + $

$\left. {\left. {^{{^{{^{{^{{^{{}}}}}}}}}} + \;{\text{6}}M\left( {\frac{{\text{1}}}{{\text{2}}} + {2\eta }\left( {{\beta } - \frac{{\text{1}}}{{\text{6}}}} \right)} \right) + M\left( {\frac{{{\text{15}}}}{{\text{2}}}{\eta } - {\text{3}} + {3\eta \beta } - {18\eta }\left( {\frac{{\beta }}{{\text{2}}} - \frac{{\text{1}}}{{\text{6}}}} \right)} \right)} \right]} \right\}{\text{,}}$

${{L}_{{т р }}} = \frac{{{{{\mu }}_{{\text{0}}}}{{l}^{{\text{2}}}}u{\text{*}}}}{{{{h}_{{\text{0}}}}}}\int\limits_{\text{0}}^{\text{1}} {\left[ {{{{\left. {\frac{{\partial {{\text{v}}_{{\text{0}}}}}}{{\partial y}}} \right|}}_{{y = {\text{0}}}}} + K{{{\left. {\frac{{\partial {{\text{v}}_{{\text{1}}}}}}{{\partial y}}} \right|}}_{{y = {\text{0}}}}}} \right]} dx = $

$ = \frac{{{{{\mu }}_{{\text{0}}}}{{l}^{2}}u{\text{*}}j}}{{{{h}_{{\text{0}}}}}}\left. {\left[ {\left( {{\text{1}} - \frac{{{13\eta }}}{{\text{2}}} + {3\eta \beta }} \right)\left( {{{{{\tilde {\mu }}}}_{{\text{0}}}} + {{{{\tilde {\mu }}}}_{{\text{1}}}}KМ } \right) + \frac{{{\text{15}}}}{{\text{2}}}{\eta }{{{\beta }}^{{\text{2}}}}\left( {{{е }^{{ - \frac{1}{\beta }}}} - {\text{1}}} \right)} \right.\left( {{{{{\tilde {\mu }}}}_{{\text{0}}}} + {{{{\tilde {\mu }}}}_{{\text{1}}}}K} \right)} \right].$

Входные параметры для расчета несущей способности и силы трения, определяемые выражениями (23), следующие:

$\eta = {\text{0}}{\text{.3}}{\kern 1pt} - {\kern 1pt} 1,\quad \omega = 0{\kern 1pt} - {\kern 1pt} 1,\quad K = 0.000022{\kern 1pt} - {\kern 1pt} 0.0052,\quad u* = 1{\kern 1pt} - {\kern 1pt} 3\;{\text{м /с }},$

$\beta = 0{\kern 1pt} - {\kern 1pt} 1,\quad \alpha = 0{\kern 1pt} - {\kern 1pt} 1,\quad {{\mu }_{0}} = 0.085\;\frac{{{\text{Н }} \cdot {\text{с }}}}{{{{{\text{м }}}^{{\text{2}}}}}},\quad p = 0,5{\kern 1pt} - {\kern 1pt} 16\;{\text{М П а ,}}$

${{p}_{a}} = 0.08{\kern 1pt} - {\kern 1pt} 0.101325\;{\text{М П а ,}}\quad {{h}_{0}} = {{10}^{7}}{\kern 1pt} - {\kern 1pt} 2 \cdot {{10}^{{ - 6}}}\;{\text{м }}.$

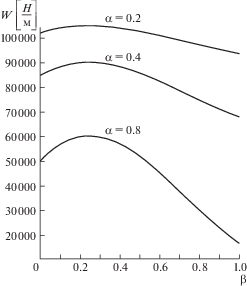
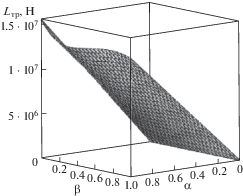
На рис. 2 и 3 представлены результаты расчетов несущей способности и силы трения от параметра α, характеризующего вязкость μ и параметра β, определяющего модуль упругости G твердого смазочного материала, а на рис. 4 и 5 показана такая же зависимость в трехмерном измерении.

Рис. 2.

Зависимость силы трения от параметра α, характеризующего зависимость вязкости смазочного материала от температуры.

Рис. 3.

Зависимость несущей способности от числа Дебора β, определяемым модулем упругости.

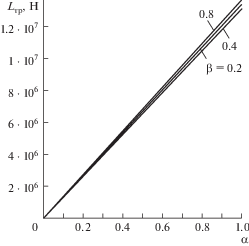
Рис. 4.

Зависимость несущей способности от числа Дебора β, определяемым модулем упругости, и от параметра α, характеризующего зависимость вязкости смазочного материала от температуры.

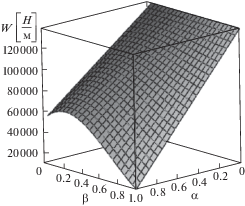
Рис. 5.

Зависимость силы трения от числа Дебора β, определяемым модулем упругости, и от параметра α, характеризующего зависимость вязкости смазочного материала от температуры.

Исследования влияния присадок. Учитывая, что рассматриваемая трибосистема работает с твердым смазочным материалом ЛЗ-ЦНИИ (ГОСТ 19791-74), работоспособность которого ограничена температурным интервалом от –40 до 100°С, был проведен целенаправленный поиск наноразмерных присадок для него, исследуя фазовые диаграммы ИК-спектроскопическим методом. Это позволило выбрать в качестве присадок поли и гетерополифосфаты [22].

Наноразмерные компоненты получали на мельнице MikroCer, размеры которых были до 45–50 нм. Для измерения размера была использована дисковая центрифуга CPS.

Следует отметить, что особенностью механического измельчения является эффект механоактивации – автовозбуждения активности вещества на стадии разрушения. Проведенные трибологические исследования показали более высокую износостойкость смазки с добавлением фосфоровольфрамата по сравнению с исходной ЛЗ-ЦНИИ за счет образования пленки на трибоповерхности.

Методом ИК-Фурье НПВО спектроскопии были проведены исследования пленок переноса, образованных в результате фрикционного контакта на торцевой машине трения в присутствии смазочной среды. На ИК-спектрах, снятых после работы трибосопряжения в течение 8 часов, кроме полос смазочного материала появляются линии 1060, 1150, 1695, 1740 и 3500–3670 см^–1, соответствующие колебаниям связей С–О–С, С=О и О–Н. В случае чистого смазочного материала после 24 часов работы трибосопряжения смазочная пленка практически не обнаруживается. Следует отметить, что пленка сохраняется на поверхности трибоконтакта даже после 8 часов работы трибосистемы. Это позволяет утверждать, что присадки значительно продлевают ресурс службы смазочного материала.

По результатам проведенных исследований можно сделать следующие

Выводы. Получена уточненная расчетная модель упорного подшипника скольжения, работающего в условиях гидродинамического смазывания расплавом легкоплавкого покрытия с учетом зависимости вязкости и модуля сдвига от температуры. Доказано, что общий эффект воздействия температуры на эти параметры заметно отклоняется от правила аддитивности и показывает: с увеличением параметра α, характеризующего зависимость вязкости смазочного материала от температуры, сила трения линейно увеличивается и практически не зависит от параметра ${\beta }$, определяемого модулем упругости (рис. 2); с увеличением параметра ${\beta }$, определяемого модулем упругости, несущая способность уменьшается, имея экстремальный характер с небольшим максимумом в области ${\beta } = {\text{0}}{\text{.2}}$; при этом с увеличением параметра α, характеризующего зависимость вязкости смазочного материала от температуры, несущая способность значительно снижается.

При рассмотрении трибосистемы, имеющей на трибоконтакте двухкомпонентную систему смазки, состоящей из минерального масла и вязкоупругого смазочного материала, обусловленного расплавом легкоплавких металлов можно получить трехкомпонентную систему смазки с получением пленки переноса на поверхности трения путем физико-химической модификации смазки нанодобавками из гетерополифосфатов. По мере работы трибосистемы в температурном интервале до 100°С смазка обеспечивает достаточно низкий коэффициент трения и высокую износостойкость. По мере увеличения температуры (до 200°С) роль смазки выполняет пленка переноса, а с ростом температуры (более 200°С) функции начинает выполнять твердый смазочный материал.

Такой подход к расчету клиновидных опор скольжения в теории трения и износа реализован впервые. Правомерность его подтверждается результатами эксперимента и полученные данные можно использовать при разработке и конструировании опор скольжения.

Работа выполнена в рамках федеральной целевой программы «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2014-2020 годы» при финансовой поддержке государства в лице Министерства науки и высшего образования России (идентификатор проекта RFMEFI60718X0203).

Список литературы

Соколов А.Г., Артемьев В.П., Чалов А.А. Исследование защитных свойств никельсодержащих диффузионных покрытий, получаемых при диффузионной металлизации стальных изделий, в сероводородных средах // Нефтегазовое дело. 2016. Доступ: http://ogbus.ru/authors/Sokolov/Sokolov_1.pdf.
Кропачев Д.Ю., Гришин А.А., Масло А.Д. Способы оперативного измерения температуры расплава металлов для нужд машиностроительных предприятий // Литье и металлургия. 2012. № 3(66). С. 126–127.
Уилсон. Смазка с расплавом // Проблемы трения и смазки. 1976. № 1. 19 с.
Беретта, Ниро, Сильвестри. Подшипники скольжения, смазываемые собственным расплавом или продуктом сублимации // Труды Америк. о-ва инж.-мех. 1992. № 1. С. 86–90.
Физические величины. Справочник. М.: Энергоатомиздат, 1991.
Хавин В.Я. Краткий химический справочник. Л.: Химия, 1991.
Перельман В.И. Краткий справочник химика. М.-Л.: Химия, 1964.
Справочник по пайке. М.: Машиностроение, 1984.
Котельницкая Л.И., Демидова Н.Н. Расчет радиальных подшипников с эффективной работой на смазке с расплавом в турбулентном режиме // Вестник РГУПС. 2002. № 2. С. 18–23.
Приходько В.М, Котельницкая Л.И. Математическая модель гидродинамической смазки при плавлении опорной поверхности радиального подшипника // Трение и износ. Гомель. 2001. Т. 22. № 6. С. 606–608.
Задорожная Е.А., Мухортов И.В., Леванов И.Г. Применение неньютоновских моделей смазочных жидкостей при расчете сложнонагруженных узлов трения поршневых и роторных машин // Трение и смазка в машинах и механизмах. 2011. № 7. С. 22–30.
Прокопьев В.Н., Бояршинова А.К., Задорожная Е.А. Динамика сложнонагруженного подшипника, смазываемого неньютоновской жидкостью // Проблемы машиностроения и надежности машин. 2005. № 6. С. 108–114.
Прокопьев В.Н., Задорожная Е.А., Караваев В.Г., Леанов И.Г. Совершенствование методики расчета сложнонагруженных подшипников скольжения, смазываемых неньютоновскими маслами // Проблемы машиностроения и надежности машин. 2010. № 1. С. 63–67.
Василенко В.В., Лагунова Е.О., Мукутадзе М.А. Гидродинамический расчет радиального подшипника, смазываемого расплавом легкоплавкого покрытия при наличии смазочного материала // Интернет-журнал “НАУКОВЕДЕНИЕ”. 2017. Т. 9. № 5. https://naukovedenie.ru/PDF/20TVN517.pdf
Ахвердиев К.С., Лагунова Е.О., Василенко В.В. Расчетная модель радиального подшипника, смазываемого расплавом, с учетом зависимости вязкости от давления // Вестник Донского гос. технич. ун-та. 2017. Т. 17. № 3(90). С. 27–37.
Lagunova E.O. Wedge-Shaped Sliding Supports Operating on Viscoelastic Lubricant Material Due to the Melt, Taking Into Account the Dependence of Viscosity and Shear Modulus on Pressure // International Journal of Applied Engineering Research ISSN 0973-4562. 2017. V. 12. № 19. P. 9120–9127.
Lagunova E.O. Radial Plain Bearings Operating on Viscoelastic Lubricant Caused by the Melt, Taking into Account the Dependence of the Viscosity of the Lubricant and the Shear Modulus on the Pressure // International Journal of Applied Engineering Research ISSN 0973-4562. 2017. V. 12. № 19. P. 9128–9137.
Vasilenko V.V., Lagunova E.O., Mukutadze M.A., Prikhodko V.M. Calculation Model of the Radial Bearing, Caused by the Melt, Taking into Account the Dependence of Viscosity on Pressure // International Journal of Applied Engineering Research ISSN 0973-4562. 2017. V. 12. № 19. P. 9138–9148.
Ахвердиев К.С., Мукутадзе М.А., Лагунова Е.О., Василенко В.В. Клиновидные опоры скольжения, работающие на микрополярном смазочном материале, обусловленные расплавом // Вестник РГУПС. 2017. № 3 (67). С. 8–15.
Lagunova E.O., Mukutadze M.A., Solop K.S. Working Out of an Analytical Model of an Axial Bearing Taking into Account Dependence of Viscous Characteristics of Micropolar Lubrication on Pressure and Temperature // International Journal of Applied Engineering Research ISSN 0973-4562. 2017. V. 12. № 14. P. 4644–4650.
Ахвердиев К.С., Колесников В.И., Приходько В.М. Основы совершенствования тяжелонагруженных узлов трения транспортных систем. Монография. М.: Маршрут, 2005.
Колесников И.В. Системный анализ и синтез процессов, происходящих в металлополимерных узлах трения фрикционного и антифрикционного назначения. М.: ВИНИТИ РАН, 2017. 384 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал