Проблемы машиностроения и надежности машин, 2019, № 1, стр. 34-43

ПОЛЕ МНОГОСЛОЙНОЙ МНОГОВИТКОВОЙ КАТУШКИ С АНАЛИТИЧЕСКИ ЗАДАННЫМИ ЗАКОНАМИ ИЗМЕНЕНИЙ РАССТОЯНИЙ МЕЖДУ СЛОЯМИ И ВИТКАМИ

А. К. Андреев^*

Московский авиационный институт (Национальный исследовательский университет)
г. Москва, Россия

Поступила в редакцию 07.08.2017

DOI: 10.1134/S0235711919010036

Аннотация

Получены формулы для расчета трехмерных магнитных полей, создаваемых сложной системой круговых токов, составляющих многослойную многовитковую катушку. Распределение векторного поля в любой области пространства можно получить, задавая аналитическую функцию, устанавливающую расстояния между витками и/или слоями. Показано, что при равномерной намотке и равенстве плотностей поверхностных токов, индукция однослойной катушки и равноразмерного аксиально намагниченного цилиндра идентичны. Индукцию цилиндра рассчитывают через размагничивающий фактор.

Термин “катушка” круговой или прямоугольной формы применяется к магнитным системам (включая плоские катушки) с небольшим отношением длины к характерному поперечному размеру. В противном случае используется термин “соленоид”. Значительный сегмент в области создания магнитных систем занимают системы кругового тока.

Методы расчетов параметров осесимметричных катушек с равномерной намоткой (без магнитного сердечника) суммированы в работе [1]. В работе [2] представлены расширенные методы расчетов, включающие моделирование систем с диамагнитными и ферромагнитными экранами и содержится базисный список литературы по рассматриваемой тематике. Задачи аналогичные [2] рассматривались в [3, 4], где в [4] учитывалась винтообразность намотки катушки. В [1, 2] расчеты выполнены в С-программе и представлены в виде изолиний или графиков.

В настоящей статье приведен метод расчета катушек с изменяемыми расстояниями между слоями и витками. В модели используются аналитические выражения для магнитного поля, что позволяет проводить расчеты в широко применяемых средах математического моделирования: Maple, MathCad, MathLab и других, где не требуются навыки программирования.

В настоящей статье представлена альтернативная математическая модель расчета индукции катушки с равномерной намоткой, основанная на вычислении компонент размагничивающего фактора аксиально намагниченного цилиндра [5]. Модель имеет преимущества по сравнению с другими методами моделирования таких систем.

Расчетная модель многослойной многовитковой катушки. В системе СИ компоненты поля токового витка записываются в виде

(1)

$\begin{gathered} {{H}_{r}}(r,z) = \frac{I}{{4\pi r}}\frac{{2z}}{{\sqrt {{{{(a + r)}}^{2}} + {{z}^{2}}} }}\left[ { - {{K}_{c}}(k) + \frac{{{{a}^{2}} + {{r}^{2}} + {{z}^{2}}}}{{{{{(a - r)}}^{2}} + {{z}^{2}}}}{{E}_{c}}(k)} \right], \\ {{H}_{z}}(r,z) = \frac{1}{{4\pi }}\frac{2}{{\sqrt {{{{(a + r)}}^{2}} + {{z}^{2}}} }}\left[ {{{K}_{c}}(k) + \frac{{{{a}^{2}} - {{r}^{2}} - {{z}^{2}}}}{{{{{(a - r)}}^{2}} + {{z}^{2}}}}{{E}_{c}}(k)} \right], \\ \end{gathered} $

где $I$ – ток витка; $2a$ – диаметр витка; $r$, $z$ – координаты точки наблюдения; ${{K}_{c}}(k)$, ${{E}_{c}}(k)$ – полные эллиптические интегралы Лежандра первого и второго рода, соответственно

(2)

${{K}_{c}}(k) = \int\limits_0^{\pi {\text{/}}2} {{{{(1 - {{k}^{2}}{{{\sin }}^{2}}\psi )}}^{{ - 1/2}}}d\psi } ,\quad {{E}_{c}}(k) = \int\limits_0^{\pi /2} {\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}\psi } } d\psi .$

Модуль интегралов равен

(3)

${{k}^{2}} = 4ar{{({{(a + r)}^{2}} + {{z}^{2}})}^{{ - 1}}}.$

На оси витка ($r = 0$) имеем: ${{H}_{r}} = 0$, ${{H}_{z}} = Ia{{({{a}^{2}} + {{z}^{2}})}^{{ - 3/2}}}$. Индукция и поле связаны соотношением $B(r,z) = {{\mu }_{0}}H(r,z)$, где ${{\mu }_{0}}$ – магнитная постоянная.

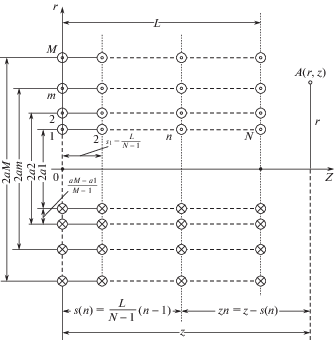
На рис. 1 показана схема расположения витков и слоев катушки; $A(r,z)$ – точка наблюдения, в которой вычисляется поле. Витки моделируются линейным круговым током (1). Начало координат расположено в торце катушки. Введены следующие обозначения. В радиальном направлении $r$: $M$ – число слоев катушки; $m$ – порядковый номер слоя ($m = 1,\; \ldots ,\;M$); $2a1$ – диаметр первого слоя; $2am$ – диаметр $m$-го слоя; $2aM$ – диаметр внешнего слоя; ($aM - a1{\text{/}}M - 1$, $M > 1$) – расстояние между слоями при равномерной намотке. Вдоль оси Z: $L$ – длина катушки; $N$ – число витков; $Z$ – расстояние от начала координат до $z$-координаты точки наблюдения $A(r,z)$; (s₁ = = $L{\text{/}}N - 1$, $N > 1$) – расстояние между витками при равномерной намотке; $s(n)$ – расстояние от начала координат до ($n - 1$)-го витка ($n = 1,\; \ldots ,\;N$); $zn$ – расстояние от ($n - 1$) витка до $z$-координаты точки наблюдения $A(r,z)$.

Рис. 1.

Полагая число витков вдоль оси $Z$ равным $N = 1$, получаем схему плоской катушки с изменяемым числом витков в радиальном направлении $r$. При числе слоев в радиальном направлении $M = 1$ схема соответствует однослойной катушке с намоткой вдоль оси $Z$.

Далее, для определенности, межслойные и межвитковые расстояния задаются степенными функциями.

Плоская катушка ($N = 1$). Результирующее поле катушки в точке наблюдения $A(r,z)$ определяется суммированием полей, создаваемых отдельными витками (1). Расстояния между слоями по $r$ задаем функцией

(4)

$Funck(aM,a1,m,k) = {{(m - {\text{1/}}M - 1)}^{k}}(aM - a1),$

где $k$ – показатель степени. Радиус m-го слоя определяется как

$am = \left| \begin{gathered} a1\quad {\text{е с л и }}\quad m = 1 \vee M = 1, \hfill \\ {\text{н е }}\;{\text{ч и с л о ,}}\;{\text{е с л и }}\quad m > M, \hfill \\ a1 + Funck(aM,a1,m,k)\quad {\text{в е з д е ,}}\;{\text{г д е }} \hfill \\ \end{gathered} \right.$

${{H}_{r}}$ и ${{H}_{z}}$ – компоненты полей, создаваемые в точке наблюдения $A$, m-м витком в соответствии с (1), (2), (3) равны

${{H}_{{rm}}}(r,z) = \left| \begin{gathered} 0,\quad {\text{е с л и }}\quad r = 0 \hfill \\ \left[ {\frac{I}{{4\pi r}}\left[ {\frac{{2z}}{{\sqrt {{{{(am + r)}}^{2}} + {{z}^{2}}} }}} \right]\left[ { - {{K}_{{cm}}}(r,z) + \left[ {\frac{{a{{m}^{2}} + {{r}^{2}} + {{z}^{2}}}}{{{{{(am - z)}}^{2}} + {{z}^{2}}}}} \right]{{E}_{{cm}}}(r,z)} \right]} \right]\quad {\text{в е з д е ,}} \hfill \\ \end{gathered} \right.$${{H}_{{zm}}}(r,z) = \frac{I}{{4\pi }}\left[ {\frac{2}{{\sqrt {{{{(am + r)}}^{2}} + {{z}^{2}}} }}} \right]\left[ {{{K}_{{cm}}}(r,z) + \left[ {\frac{{a{{m}^{2}} - {{r}^{2}} - {{z}^{2}}}}{{{{{(am - z)}}^{2}} + {{z}^{2}}}}} \right]{{E}_{{cm}}}(r,z)} \right],$

${\text{г д е }}\quad {{K}_{{cm}}}(r,z) = \int\limits_0^{\pi /2} {{{{(1 - k_{m}^{2}{{{\sin }}^{2}}\psi )}}^{{ - 1/2}}}d\psi } ,\quad {{E}_{{cm}}}(r,z) = \int\limits_0^{\pi /2} {\sqrt {1 - k_{m}^{2}{{{\sin }}^{2}}\psi } d} \psi ,$

$k_{m}^{2} = 4(am)r{{({{z}^{2}} + {{(am + r)}^{2}})}^{{ - 1}}}.$

Модуль поля, создаваемого m-м витком записывается в виде

${{H}_{m}}{\text{mod(}}r,z{\text{)}} = \sqrt {{{H}_{{rm}}}{{{(r,z)}}^{2}} + {{H}_{{zm}}}{{{(r,z)}}^{2}}} .$

Суммарные аксиальная ${{H}_{z}}$ и радиальная ${{H}_{r}}$ компоненты полей плоской катушки и модуль суммарного поля ${{H}_{m}}{\text{mod(}}r,z{\text{)}}$ вычисляются по формулам

$\begin{gathered} H{{r}_{m}}(r,z) = \sum\limits_{m = 1}^M {{{H}_{{rm}}}} (r,z),\quad H{{z}_{m}}(r,z) = \sum\limits_{m = 1}^M {{{H}_{{zm}}}} (r,z), \\ {{H}_{m}}{\text{mod(}}r,z{\text{)}} = \sqrt {H{{r}_{m}}{{{(r,z)}}^{2}} + H{{z}_{m}}{{{(r,z)}}^{2}}} . \\ \end{gathered} $

При $k = 1$ формулы определяют поле плоской катушки с равными расстояниями между витками.

Однослойная катушка с произвольным шагом намотки ($M = 1$). Закон изменения межвиткового расстояния по $z$ задаем функцией

(5)

$Funct(n,L) = {{(n - {\text{1/}}N - 1)}^{t}}L,$

где $t$ – показатель степени, $n{\text{ }} = 1, \ldots ,\;N$. Расстояния $s(n)$ и $zn$ имеют вид

$s(n) = \left| \begin{gathered} 0,\quad {\text{е с л и }}\quad n = 1, \hfill \\ NaN,\quad {\text{е с л и }}\quad n > {\rm N}, \hfill \\ Funct(n,L),\quad {\text{в е з д е ,}}\quad zn = z - Funct(n,L). \hfill \\ \end{gathered} \right.$

Радиальная $r$- и $z$-компоненты полей ${{H}_{r}}$ и ${{H}_{z}}$, создаваемые в точке наблюдения $A{\text{(}}r,z{\text{)}}$ $n$-м витком, следуют из формул

${{H}_{{rn}}}(r,z) = \left| \begin{gathered} 0,\quad {\text{е с л и }}r = {\text{0,}} \hfill \\ \frac{I}{{4\pi r}}\left[ {\frac{{2zn}}{{\sqrt {z{{n}^{2}} + (a1 + r)} }}} \right] - {{K}_{{cn}}}(r,z,n) + \left[ {\frac{{a{{1}^{2}} + {{r}^{2}} + z{{n}^{2}}}}{{{{{(a1 - r)}}^{2}} + z{{n}^{2}}}}} \right]{{E}_{{cn}}}(r,z,n)\quad {\text{в е з д е ,}} \hfill \\ \end{gathered} \right.$

${{H}_{{zn}}}(r,z) = \frac{I}{{4\pi }}\left[ {\frac{2}{{{{{(a1 + r)}}^{2}} + z{{n}^{2}}}}} \right]\left[ {{{K}_{{cn}}}(r,z,n) + \left[ {\frac{{a{{1}^{2}} - {{r}^{2}} - z{{n}^{2}}}}{{{{{(a1 - r)}}^{2}} + z{{n}^{2}}}}} \right]{{E}_{{cn}}}(r,z,n)} \right],$

${{K}_{{cn}}}(r,z,n) = \int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {{{{(1 - k_{n}^{2}{{{\sin }}^{2}}\psi )}}^{{ - \frac{1}{2}}}}} d\psi ,\quad {{E}_{{cn}}}(r,z,n) = \int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {\sqrt {1 - k_{n}^{2}{{{\sin }}^{2}}\psi } } d\psi ,$

$k_{n}^{2} = 4a{\text{1}}r{{(z{{n}^{2}} + {{(a{\text{1}} + r)}^{2}})}^{{ - 1}}}.$

Модуль поля, создаваемого $n$-м витком рассчитывается по формуле

${{H}_{n}}\bmod (r,z) = \sqrt {{{H}_{{rn}}}{{{(r,z)}}^{2}} + {{H}_{{zn}}}{{{(r,z)}}^{2}}} .$

Суммарные аксиальная ${{H}_{z}}$ и радиальная ${{H}_{r}}$ компоненты полей равны

$H{{z}_{n}}(r,z) = \sum\limits_{n = 1}^N {{{H}_{{zn}}}(r,z)} ,\quad H{{r}_{n}}(r,z) = \sum\limits_{n = 1}^N {{{H}_{{rn}}}(r,z)} ,$

откуда следует модуль суммарного поля

${{H}_{n}}\bmod (r,z) = \sqrt {H{{z}_{n}}{{{(r,z)}}^{2}} + H{{r}_{n}}{{{(r,z)}}^{2}}} .$

Многослойная многовитковая катушка ($N,\,\,M$). Расстояния между витками и слоями задаются в соответствии с определениями (4), (5). Компоненты полей следуют из соотношений

${{H}_{{rmn}}}(r,z) = \left| \begin{gathered} 0,\quad {\text{е с л и }}\quad r = 0 \hfill \\ \left( {\frac{I}{{4\pi }}} \right)\left[ {\frac{{2zn}}{{\sqrt {{{{(am + r)}}^{2}} + z{{n}^{2}}} }}} \right]\left[ { - {{K}_{{cmn}}}(r,z) + \left[ {\frac{{a{{m}^{2}} + {{z}^{2}} + z{{n}^{2}}}}{{{{{(am - r)}}^{2}} + z{{n}^{2}}}}} \right]{{E}_{{cmn}}}(r,z)} \right] \hfill \\ \end{gathered} \right.\quad {\text{в е з д е ,}}$${{H}_{{zmn}}}(r,z) = \left( {\frac{I}{{4\pi }}} \right)\left[ {\frac{2}{{\sqrt {\left( {{{{\left( {am + r} \right)}}^{2}} + z{{n}^{2}}} \right)} }}} \right]\left[ {{{K}_{{cmn}}}(r,z) + \left[ {\frac{{a{{m}^{2}} - {{r}^{2}} - z{{n}^{2}}}}{{{{{\left( {am - r} \right)}}^{2}} + z{{n}^{2}}}}} \right]{{E}_{{cmn}}}(r,z)} \right],$

где

${{K}_{{cmn}}}(r,z) = \int\limits_0^{\pi /2} {{{{(1 - k_{{mn}}^{2}{{{\sin }}^{2}}\psi )}}^{{ - 1/2}}}} d\psi ,\quad {{E}_{{cmn}}}(r,z) = \int\limits_0^{\pi /2} {\sqrt {1 - k_{{mn}}^{2}{{{\sin }}^{2}}\psi } } d\psi ,$

$k_{{mn}}^{2} = 4amr{{(z{{n}^{2}} + {{(am + r)}^{2}})}^{{ - 1}}}.$

Суммарные аксиальные и радиальные компоненты полей катушки вычисляются по формулам

(6)

$H{{r}_{{mn}}}(r,z) = \sum\limits_{m = 1}^M {\left( {\sum\limits_{n = 1}^N {{{H}_{{rmn}}}(m,r,z,n)} } \right)} ,\quad H{{z}_{{mn}}}(r,z) = \sum\limits_{m = 1}^M {\left( {\sum\limits_{n = 1}^N {{{H}_{{zmn}}}(m,r,z,n)} } \right)} .$

Из (6) следует модуль поля катушки

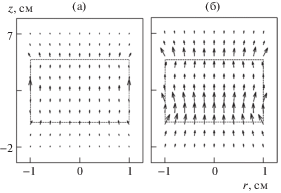
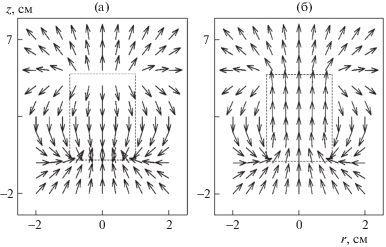
${{H}_{{{\text{mn}}}}}\bmod {\text{(}}r,z) = \sqrt {H{{r}_{{mn}}}{{{(r,z)}}^{2}} + H{{z}_{{mn}}}{{{(r,z)}}^{2}}} .$

На рис. 2 приведен график векторного поля компонент катушки $H{{r}_{{mn}}}$, $H{{z}_{{mn}}}$ (6) в плоскости $r - z$ в диапазоне (–1 см ≤ r ≤ 1 см, $ - 2 \leqslant z \leqslant 7$ см) при входных параметрах: число слоев $M = 5$, число витков $N = 3$, диаметр первого слоя $2a1 = 2$ см, диаметр внешнего слоя $aM = 7$ см, длина катушки $L = 5$ см. Пунктирной линией показаны границы катушки. Расчеты проводили в системе вычислений MathCad 14.

Рис. 2.

График векторного поля катушки. а – показатель степени в радиальном направлении, $k = 2$-квадратичная зависимость межслойных расстояний, показатель степени в $Z$-направлении $t = 1$ – равные расстояния между витками; б – $k = 2$, $t = 2$ – квадратичная зависимость межслойных и межвитковых расстояний.

В зависимости от значений показателей степени, входящих в определяющие формулы (4), (5), получаем следующие модификации магнитной системы: 1) $k = 1$ – равные расстояния между витками в радиальном направлении при заданном законе изменения расстояний в $z$-направлении; 2) $t = 1$ – равные расстояния между витками в $z$-направлении при заданном законе изменения расстояний в радиальном $r$-направлении; 3) $k = 1$ и $t = 1$ – равные расстояния между витками в радиальном $r$- и $z$-направлениях; 4) $M = 1$ – однослойная катушка при заданном законе изменения расстояний в $z$-направлении; 5) $M = 1$, $t = 1$ – однослойная катушка при равных расстояниях между витками в $z$-направлении; 6) $M = 2,$ $t = 1$ при противоположных направлениях токов в слоях и плотной намотке – аналог аксиально намагниченного тора [6] (см. далее); 7) $N = 1$ – плоская (дисковая) катушка при заданном законе изменения расстояний в радиальном направлении; 8) $N = 1$, $k = 1$ – плоская (дисковая) катушка при равных расстояниях в радиальном направлении; 9) $M = 1$, $N = 1$ – одиночный круговой токовый виток.

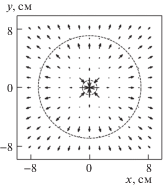
На рис. 3 приведен график векторного поля радиальной компоненты катушки $H{{r}_{{mn}}}$ (6) в плоскости ($x - y$) при $z = 3.7$ см ($L = 5$ см, $a = 1$ см, $aM = 7$ см, $N = 3$, $M = 5$, $t = 2$, $k = 2$).

Рис. 3.

Компоненты поля ${{H}_{x}}$, ${{H}_{y}}$ записываются следующим образом:

$r(x,y) = \sqrt {{{x}^{2}} + {{y}^{2}}} ,\quad q(x,y) = x{{({{x}^{2}} + {{y}^{2}})}^{{ - 1/2}}},\quad g(x,y) = y{{({{x}^{2}} + {{y}^{2}})}^{{ - 1/2}}},$

$Hx(x,y,z) = H{{r}_{{mn}}}(r,z)q(x,y),\quad Hy(x,y,z) = H{{r}_{{mn}}}(r,z)g(x,y).$

Рисунок 3 построен в пределах (–8 см ≤ x, y ≤ 8 см). Выделенная точками область показывает границы сечения обмотки $2a1 = 2$ см и $2aM = 14$ см.

Эквивалентность магнитной индукции аксиально намагниченного цилиндра и однослойной катушки с постоянным шагом намотки. Рассмотрим метод расчета индукции ${{{\mathbf{B}}}_{c}}$ аксиально намагниченного цилиндра. Начало координат расположено в торце цилиндра и совпадает с началом координат равноразмерной однослойной катушки. Схематично поле цилиндра ${{H}_{p}}$ и линии индукции катушки $B$ показаны на рис. 4.

Рис. 4.

Поля рассеяния и размагничивания цилиндра согласно “зарядовой” модели (а); индукция цилиндра в соответствии с моделью поверхностных токов (б); Индукция цилиндра совпадает с индукцией катушки.

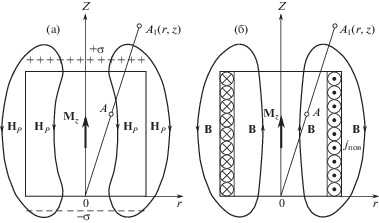
Поверхностные дивергенция и ротор намагниченности цилиндра ${{{\mathbf{M}}}_{z}}$ определяют плотности поверхностного “магнитного заряда” на торцах цилиндра $\sigma = - {\text{Div}}\,{{{\mathbf{M}}}_{z}}$ (рис. 4, а) и поверхностного тока на боковой поверхности ${{{\mathbf{j}}}_{{{\text{п о в }}}}} = \operatorname{Rot} {{{\mathbf{M}}}_{z}}$ (рис. 4, б), соответственно. В системе СИ (в вакууме) $\sigma $, ${{j}_{{{\text{п о в }}}}}$ и ${{M}_{z}}$ связаны простыми соотношениями: $\sigma = {\mathbf{Mn}}$ А/м, ${{{\mathbf{j}}}_{{{\text{п о в }}}}} = [{{{\mathbf{M}}}_{z}}{\mathbf{n}}]$ А/м (${\mathbf{n}}$ – нормаль к поверхностям цилиндра). Объемные “магнитные заряды” при однородной намагниченности равны нулю. Точками $A$ и ${{A}_{1}}(r,z)$ обозначены точки наблюдения.

Поверхностные “заряды” $\sigma $ создают размагничивающее поле ${{H}_{р }}$ объеме цилиндра, направленное противоположно ${{M}_{z}}$ (рис. 4, а) и поле рассеяния вне цилиндра (обозначаемое ${{H}_{p}}$). Размагничивающий фактор, определяющий размагничивающее поле цилиндра, имеет две компоненты ${{N}_{{r\,z}}}(r,z)$ и ${{N}_{{z\,z}}}(r,z)$. Компоненты ${{H}_{р }}$ и ${{M}_{z}}$ связаны соотношением ${{H}_{{ip}}} = - {{N}_{{iz}}}{{M}_{z}}$ ($i = r,z$). Размагничивающий фактор может принимать значения $0 \leqslant \sum\limits_i {{{N}_{{ip}}}} \leqslant 1$.

На рис. 4, б показаны линии индукции, создаваемые однослойной катушкой ($M = 1$, $t = 1$) с числом витков ${{N}_{c}}$. Плотность поверхностного тока катушки равна $j = {{N}_{c}}I{\text{/}}L$ А/м. Расчеты показывают, что при условии равенства плотностей поверхностных токов катушки и цилиндра $j = {{j}_{{{\text{п о в }}}}}$ намагниченность цилиндра ${{M}_{z}} = {{j}_{{{\text{п о в }}}}}$ создает индукцию ${{{\mathbf{B}}}_{c}}$, эквивалентную индукции катушки ${{B}_{n}}$ [7].

В [5] получены формулы для расчета полей аксиально намагниченного цилиндра

(7)

${{H}_{r}}\left( {r,z} \right) = - {{N}_{{rz}}}{{M}_{z}} = - {{M}_{z}}\left| \begin{gathered} \frac{1}{2}a\int\limits_0^\infty {{{J}_{1}}(tr){{J}_{1}}(ta)} [{{e}^{{ - tz}}} - {{e}^{{ - t\left( {L - z} \right)}}}]dt,\quad {\text{е с л и }}\quad \left( {0 \leqslant z \leqslant L} \right), \hfill \\ \frac{1}{2}a\int\limits_0^\infty {{{J}_{1}}(tr){{J}_{1}}(ta)} [{{e}^{{ - tz}}} - {{e}^{{t\left( {L - z} \right)}}}]dt,\quad {\text{е с л и }}\quad \left( {z \succ L} \right), \hfill \\ \frac{1}{2}a\int\limits_0^\infty {{{J}_{1}}(tr){{J}_{1}}(ta)[{{e}^{{tz}}} - {{e}^{{ - t\left( {L - z} \right)}}}]} dt,\quad {\text{е с л и }}\quad \left( {z \prec 0} \right); \hfill \\ \end{gathered} \right.$

(8)

${{H}_{z}}\left( {r,z} \right) = - {{N}_{{zz}}}{{M}_{z}} = - {{M}_{z}}\left| \begin{gathered} \frac{1}{2}a\int\limits_0^\infty {{{J}_{0}}(tr){{J}_{1}}(ta)} [{{e}^{{ - tz}}} + {{e}^{{ - t\left( {L - z} \right)}}}]dt,\quad {\text{е с л и }}\quad \left( {0 \leqslant z \leqslant L} \right), \hfill \\ \frac{1}{2}a\int\limits_0^\infty {{{J}_{0}}(tr){{J}_{1}}(ta)} [{{e}^{{ - tz}}} - {{e}^{{t\left( {L - z} \right)}}}]dt,\quad {\text{е с л и }}\quad \left( {z \succ L} \right), \hfill \\ \frac{1}{2}a\int\limits_0^\infty {{{J}_{0}}(tr){{J}_{1}}(ta)} [{{e}^{{ - t\left( {L - z} \right)}}} - {{e}^{{tz}}}]dt,\quad {\text{е с л и }}\quad \left( {z \prec 0} \right), \hfill \\ \end{gathered} \right.$

где ${{H}_{r}}(r,z)$ и ${{H}_{z}}(r,z)$ – радиальная $r$- и аксиальная $z$-компоненты поля, соответственно; ${{J}_{0}}(tr)$ и ${{J}_{1}}(ta)$ – функции Бесселя от действительного аргумента нулевого и первого порядка. Уравнения (7), (8) определяют поля размагничивания ${{H}_{p}}$ в объеме цилиндра и поля рассеяния ${{H}_{p}}$ вне цилиндра.

Индукция ${{B}_{c}}$ связана с ${{{\mathbf{H}}}_{p}}$ и ${{{\mathbf{M}}}_{z}}$ соотношением

(9)

${{{\mathbf{B}}}_{c}} = {{\mu }_{0}}\left( {{{{\mathbf{H}}}_{p}} + {{{\mathbf{M}}}_{z}}} \right).$

Линии индукции непрерывны и из уравнения (9) следуют формулы, определяющие ${{{\mathbf{B}}}_{c}}$ как в объеме цилиндра, так и вне его

(10)

${{B}_{r}}(r,z) = {{\mu }_{0}}{{H}_{r}}(r,z),$

(11)

${{B}_{z}}(r,z) = \left| \begin{gathered} {{\mu }_{0}}({{H}_{z}}(r,z) + {{M}_{z}}),\quad {\text{е с л и }}\quad 0 < z \leqslant L \wedge \left| r \right| < a, \hfill \\ {{\mu }_{0}}{{H}_{z}}(r,z)\quad {\text{в е з д е }}{\text{.}} \hfill \\ \end{gathered} \right.$

Модуль индукции равен ${{B}_{c}}\bmod (r,z) = \sqrt {{{B}_{r}}{{{(r,z)}}^{2}} + {{B}_{z}}{{{(r,z)}}^{2}}} $.

На рис. 5 построены нормализованные графики векторного поля цилиндра (7), (8) и индукции (10), (11) в плоскости ($r - z$) с входными параметрами $L = 5$ см, $а = 1$ см, (–4 см ≤ r ≤ 4 см, –2 см ≤ z ≤ 7 см). При числе витков катушки $N \geqslant 30$ графики индукции цилиндра и катушки практически идентичны. Точками показаны границы цилиндра.

Рис. 5.

Размагничивающее поле и поле рассеяния цилиндра (а); б – индукция цилиндра и однослойной катушки при плотной намотке.

На рис. 6 приведены графики индукций, создаваемых обтекаемым током цилиндром (8) и катушкой с равномерной намоткой (5) ($t = 1$), вдоль линии, смещенной в радиальном направлении относительно оси $Z$ на расстояние $r = 0.1$ см. Здесь же приведены также графики $Z$-компоненты размагничивающего поля цилиндра (8). Ток в каждом витке принят равным $I = 3$ А. Размеры эквивалентных магнитных систем: диаметр $2а = 2$ см, длина $L = 5$ см.

Рис. 6.

Символьная линия – индукция обтекаемого током цилиндра; сплошная линия – индукция равноразмерной однослойной катушки с равномерной намоткой; точечная линия $z$-компонента размагничивающего поля цилиндра ${{H}_{{zp}}}$; а – число витков катушки $N = 3$, $j = {{M}_{z}} = 180$ А/м, б – $N = 100$, $j = {{M}_{z}} = 6 \cdot {{10}^{3}}$ А/м.

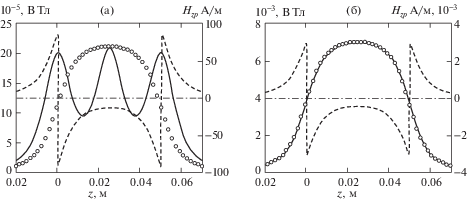
Рисунки показывают, что при числе витков $N \geqslant 100$ индукции катушки и цилиндра практически совпадают. При $N = 30$ разница максимальных значений индукций вблизи оси $Z$составляет ∼1.4%.

Выводы. Приведенные в статье результаты показали работоспособность предложенных методов расчета полей. Задание расстояний между слоями и витками катушки, изменяющимися по заранее заданному закону, является эффективным методом создания требуемой топологии поля. Модель позволяет рассчитывать межвитковую индукцию. В частном, но практически важном случае при равномерной намотке ($t = 1$), индукцию катушек ${{B}_{c}}$ целесообразно определять с использованием модели аксиально намагниченного цилиндра, обеспечивающей несопоставимо меньшее время компьютерных расчетов. Так, при $N = 1000$ витков ($L = 9$ см, шаг 0.1 см) время построения графика индукции катушки ${{B}_{c}}$ (рис. 6, б) на стандартном персональном компьютере составляет ~4.8 минуты. Такие же вычисления по модели цилиндра занимают доли секунды. Время расчета индукции ${{B}_{c}}$ пропорционально числу витков $N$. В расчетные формулы цилиндра входит намагниченность ${{M}_{z}}$, и время счета не зависит от числа витков.

Представленная модель органично встраивается в сложные вычислительные эксперименты и не влияет на временные параметры основной программы [8]. Используя модель цилиндра легко составить систему, аналогичную многослойной катушке. Два соосных цилиндра равной длины с противоположным направлением намагниченности ${{M}_{z}}$ образуют аксиально намагниченный тор.

В [5] приведены программы расчета тензора размагничивания прямоугольной призмы. Расчет полей и индукции призмы можно выполнить аналогично модели, представленной в статье. Из системы невзаимодействующих аксиально намагниченных цилиндров и однородно намагниченных призм легко создать сложную конфигурацию источников поля не обладающую симметрией по $r$.

Уравнения (7), (8) цилиндра при $L \gg a$ определяют поля торцевых разноименно “заряженных” дисков. При $L \ll a$ получаем двойной заряженный слой. Производные от энергии размагничивания ферромагнетика $E = 1{\text{/}}2\int {{\mathbf{M}}{{{\mathbf{H}}}_{p}}d\text{v}} $ по соответствующему параметру позволяют рассчитывать силы, действующие на поверхность образца.

Список литературы

Алиевский Б.Л., Орлов В.Л. Расчет параметров магнитных полей осесимметричных катушек: Справочник. М.: Энергоатомиздат, 1983. 112 с.
Алиевский Б.Л., Октябрьский А.М., Орлов В.Л., Постников В.А. Моделирование магнитных полей осесимметричных систем / Под. ред. Б.Л. Алиевского. М.: Изд-во МАИ, 2007. 317 с.
Штамбергер Г.А. Устройства для создания слабых постоянных магнитных полей / Под ред. К.Б. Карандеева. Новосибирск: Изд-во Наука, 1972. 176 с.
Бухгольц Г. Расчет электрических и магнитных полей. М.: Изд-во ин. лит-ры, 1961. 712 с.
Андреев А.К. Магнитостатика ферромагнетиков. М.: Изд-во МАИ, 2011. 162 с.
Андреев А.К. Пондеромоторные силы в системе “аксиально намагниченный тор – магнитомягкий шар” // Вестник московского авиационного института. 2015. Т. 22. № 4. С. 149–158.
Парсел Э. Электричество и магнетизм. М.: Наука, 1975. 439 с.
Котельников В.А., Котельников М.В., Морозов А.В. Математическое моделирование взаимодействия потока разреженной плазмы с магнитным полем. М.: Изд-во МАИ, 2015. 169 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал