Проблемы машиностроения и надежности машин, 2019, № 1, стр. 66-73

ОСНОВНОЕ НАПРЯЖЕННО-ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ КРУГЛОЙ ПЛАСТИНКИ ПЕРЕМЕННОЙ ТОЛЩИНЫ НА ОСНОВЕ НЕКЛАССИЧЕСКОЙ ТЕОРИИ

В. В. Фирсанов^*

Московский авиационный институт (Национальный исследовательский университет)
Москва, Россия

Поступила в редакцию 04.12.2017

DOI: 10.1134/S0235711919010073

Аннотация

Разработана математическая модель основного напряженно-деформированного состояния круглой пластинки с несимметрично меняющейся переменной толщиной при осесимметричном нагружении. Применяется метод прямого асимптотического интегрирования дифференциальных уравнений трехмерной теории упругости. Сформулирована краевая задача, представляющая собой систему двух дифференциальных уравнений в перемещениях второго и четвертого порядков с переменными коэффициентами и соответствующими граничными условиями. Приведен пример расчета пластинки, выполненный в системе “Mathlab-14” методом конечных разностей.

В современных условиях проектирования авиационной и ракетно-космической техники, определяемых разработкой новых конструктивно-силовых схем летательных аппаратов, интенсификацией и расширением спектра внешних воздействий, а также внедрением перспективных материалов, предъявляются повышенные требования к точности методов расчета напряженно-деформированного состояния (НДС) конструкций, обеспечивающих безопасную работу на пределе возможности материала при выполнении требований весового совершенства. Отметим, что не потеряли своего значения более оперативные, по отношению к численным, методы расчета НДС, основанные на аналитических моделях, в том числе, типа пластинок и оболочек с существенно переменными жесткостными характеристиками.

В настоящей статье рассматривается уточненный метод расчета круглой пластинки переменной толщины, расчетная схема которой используется при анализе прочности и долговечности таких элементов конструкций, как плоские днища резервуаров и теплообменных аппаратов, элементы различных силовых приводов и др.

Один из возможных путей построения математически обоснованной теории пластин и оболочек состоит в применении метода прямого асимптотического разложения компонентов НДС в ряды по малому параметру – относительной толщине трехмерного тела и в последующем интегрировании уравнений трехмерной теории упругости. С помощью этого метода в работе [1] были сформулированы варианты приближенных теорий, уточняющих результаты классической теории не только во внутренних областях пластинок и оболочек, но и в их узких краевых зонах. Однако, сформулированные краевые задачи, в силу сложности соответствующих им дифференциальных уравнений и различного типа граничных условий, напрямую решить затруднительно. В связи с этим в [2–4] краевые задачи с помощью вариационного метода Власова–Канторовича и специально подобранных аппроксимирующих полиномов решены и доведены до численных результатов, в том числе для прямоугольных пластинок и цилиндрических оболочек переменной толщины [5].

Отметим, что уточненные варианты расчета общего НДС круглых пластинок, построены для постоянной толщины и частного случая [6] переменной толщины, симметричной относительно оси, проходящей через центр масс поперечных сечений. Известно, что многие элементы авиационных конструкций оформляются в виде пластинок и оболочек переменной толщины таким образом, что одно из их оснований наклонено под некоторым углом к другому основанию. Расчетные схемы этих элементов конструкции разработаны [5] на основе метода прямого асимптотического интегрирования.

Аналогичные приведенным расчетные схемы несимметричных элементов конструкций разработаны в [7] с помощью другого подхода, заключающегося в разложении компонентов НДС в ряды по нормальной к срединной поверхности координате с последующим применением вариационного принципа Лагранжа. Отметим, что результаты соответствующие двум приведенным подходам имеют хорошее качественное и количественное совпадение.

В настоящей статье математический аппарат применяется для построения основного НДС круглой пластинки с несимметрично изменяющейся переменной толщиной.

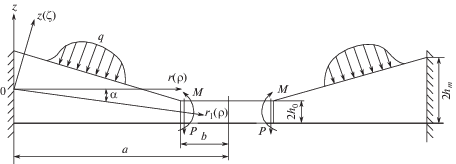
Постановка задачи. Пусть изотропная пластинка (рис. 1) с круглым отверстием в центре находится под действием симметричной поперечной нагрузки q(z). Отнесем пластинку к цилиндрической системе координат (r, θ, z), обозначив через a и b радиусы внешнего и внутреннего контуров, а через 2h – ее переменную толщину, определяемую соотношением

$h = {{h}_{m}} - r\operatorname{tg} \alpha ,\quad {\text{г д е }}\quad \operatorname{tg} \alpha = \frac{{{{h}_{m}} - {{h}_{0}}}}{{a - b}}.$

Рис. 1.

Круглая пластинка переменной толщины.

Для определенности будем полагать, что контур пластинки r = 0 жестко защемленный. Внутренний контур пластинки r = a – b может быть любым, в том числе свободным, нагруженным краевыми усилиями типа изгибающих моментов, поперечных и нормальных сил.

Наряду с цилиндрической системой координат $\left( {r,\theta ,z} \right)$ будем рассматривать косоугольную систему $\left( {{{r}_{1}},\theta ,{{z}_{1}}} \right)$, для которой справедливы равенства

(1)

${{r}_{1}} = \frac{r}{{\cos \alpha }},\quad {{z}_{1}} = z + {{r}_{1}}\sin \alpha .$

Исходная система уравнений плоской задачи теории упругости в косоугольной системе координат получается из соответствующей системы уравнений в цилиндрических координатах путем перехода от производных $\frac{\partial }{{\partial r}}$, $\frac{\partial }{{\partial {\text{z}}}}$ к производным $\frac{\partial }{{\partial {{r}_{1}}}}$, $\frac{\partial }{{\partial {{{\text{z}}}_{{\text{1}}}}}}$ по формулам

$\frac{\partial }{{\partial r}} = \frac{1}{{\cos \alpha }}\frac{\partial }{{\partial {{r}_{1}}}} + \operatorname{tg} \alpha \frac{\partial }{{\partial {{z}_{1}}}},\quad \frac{\partial }{{\partial z}} = \frac{\partial }{{\partial {{z}_{1}}}}$

и введения безразмерной системы координат с помощью равенств ${{r}_{1}} = c{{\rho }_{1}}$, ${{z}_{1}} = h\zeta $, $c = a - b$, полагая, что по $\left( {{{\rho }_{1}},\theta ,\zeta } \right)$ изменяемость искомого НДС не слишком велика.

Применяя метод асимптотического интегрирования уравнений теории упругости, построим математическую модель основного НДС. При интегрировании уравнений теории упругости все напряжения и перемещения Φ принимаем в виде

(2)

$\Phi = h_{*}^{{ - p}}\sum\limits_{s = 1}^\infty {h_{*}^{{(s - 1)}}{{\Phi }^{{(s)}}},} $

где p – целое число, которое задается разным для различных перемещений и напряжений, т.е. для различных s: ${{h}_{ * }} = {h \mathord{\left/ {\vphantom {h с }} \right. \kern-0em} с }$, а также учитываем граничные условия на верхней и нижней плоскостях пластинки

(3)

$\begin{gathered} {{\sigma }_{z}} + 2\operatorname{tg} \alpha {{\tau }_{{rz}}} = - q;\quad {{\tau }_{{rz}}} + 2\operatorname{tg} \alpha {{\sigma }_{r}} = - 2\operatorname{tg} \alpha q\quad {\text{п р и }}\quad {{z}_{1}} = h; \\ {{\sigma }_{z}} = {{\tau }_{{rz}}} = 0\quad {\text{п р и }}\quad {{z}_{1}} = - h. \\ \end{gathered} $

Для основного напряженного состояния выберем p в (2) следующим образом: p = 2 для ${{\sigma }_{r}},{{\sigma }_{\theta }}$; p = 0 для ${{\sigma }_{z}}$; p = 1 для ${{\tau }_{{rz}}}$; p = 2 для u; p = 3 для w. Подставим ряд (2) в исходную систему уравнений в косоугольных координатах (1), которая здесь не приводится.

Основное НДС. Следуя работам [2, 5], для определения искомых величин получим систему уравнений

(4)

$\begin{gathered} {{\chi }_{1}}\sigma _{r}^{{}} + \frac{{\partial \tau _{{rz}}^{{}}}}{{\partial \zeta }} + \frac{{\sigma _{r}^{{}} - \sigma _{\theta }^{{}}}}{\rho } = 0,\quad {{\chi }_{1}}\tau _{{rz}}^{{}} + \frac{{\partial \sigma _{z}^{{}}}}{{\partial \zeta }} + \frac{{\tau _{{rz}}^{{}}}}{\rho } = 0,\quad Eu = c(\sigma _{r}^{{}} - \nu \sigma _{\theta }^{{}}), \\ E\frac{u}{\rho } = c(\sigma _{\theta }^{{}} - \nu \sigma _{r}^{{}}),\quad E\frac{{\partial w}}{{\partial \zeta }} = 0,\quad E\left( {{{\chi }_{1}}w + \frac{{\partial u}}{{\partial \zeta }}} \right) = 0, \\ \end{gathered} $

где через χ₁ обозначен дифференциальный оператор

${{\chi }_{1}} = \frac{\partial }{{\partial \rho }} + \operatorname{tg} \alpha h_{ * }^{{\left( { - 1} \right)}}\frac{\partial }{{\partial \zeta }} + p\operatorname{tg} \alpha h_{ * }^{{\left( { - 1} \right)}} = 0\quad {\text{и }}\quad \rho = {{\rho }_{1}}\cos \alpha .$

Область применимости уравнений (4) ограничена неравенством $h_{ * }^{2}$ < tgα < $h_{ * }^{0}$

Перейдем в системе уравнений (4) к величинам, стоящим в левой части разложения (2) и, интегрируя ее, найдем

(5)

$\begin{gathered} w = w(\rho ),\quad u = \zeta {{u}_{1}} + {{u}_{0}},\quad {{\sigma }_{r}} = \zeta {{\sigma }_{{r1}}} + {{\sigma }_{{r0}}},\quad {{\sigma }_{\theta }} = \zeta {{\sigma }_{{\theta 1}}} + {{\sigma }_{{\theta 0}}}, \\ {{\tau }_{{rz}}} = {{\zeta }^{2}}{{\tau }_{{rz2}}} + \zeta {{\tau }_{{rz1}}} + {{\tau }_{{rz0}}},\quad {{\sigma }_{z}} = {{\zeta }^{3}}{{\sigma }_{{z3}}} + {{\zeta }^{2}}{{\sigma }_{{z2}}} + \zeta {{\sigma }_{{z1}}} + {{\sigma }_{{z0}}}. \\ \end{gathered} $

Здесь величины, отмеченные дополнительными числовыми индексами внизу, функции переменной ρ, связанные следующими равенствами:

${{u}_{1}} = - {{h}_{ * }}\frac{{dw}}{{d\rho }},\quad {{\sigma }_{{r1}}} = - \frac{E}{{(1 - {{v}^{2}})c}}\left[ {{{h}_{ * }}\frac{{{{d}^{2}}w}}{{d{{\rho }^{2}}}} + \left( {\frac{{v{{h}_{ * }}}}{\rho } - \operatorname{tg} \alpha } \right)\frac{{dw}}{{d\rho }}} \right],$

${{\sigma }_{{r0}}} = - \frac{E}{{(1 - {{v}^{2}})c}}\left( {\frac{{d{{u}_{0}}}}{{d\rho }} + v\frac{{{{u}_{0}}}}{\rho } - \operatorname{tg} \alpha \frac{{dw}}{{d\rho }}} \right),$

${{\sigma }_{{\theta 1}}} = - \frac{{vE}}{{(1 - {{v}^{2}})c}}\left[ {{{h}_{ * }}\frac{{{{d}^{2}}w}}{{d{{\rho }^{2}}}} + \left( {\frac{{{{h}_{ * }}}}{{\nu \rho }} - \operatorname{tg} \alpha } \right)\frac{{dw}}{{d\rho }}} \right],$

${{\sigma }_{{\theta 0}}} = \frac{E}{{(1 - {{v}^{2}})c}}\left[ {\frac{{{{u}_{0}}}}{\rho } + v\left( {\frac{{d{{u}_{0}}}}{{d\rho }} - \operatorname{tg} \alpha \frac{{dw}}{{d\rho }}} \right)} \right],$

${{\tau }_{{rz2}}} = \frac{{E{{h}_{ * }}}}{{2(1 - {{v}^{2}})c}}\left[ {{{h}_{ * }}\frac{{{{d}^{3}}w}}{{d{{\rho }^{3}}}} + \left( {\frac{{{{h}_{ * }}}}{\rho } - 2\operatorname{tg} \alpha } \right)\frac{{{{d}^{2}}w}}{{d{{\rho }^{2}}}} - \frac{1}{\rho }\left( {\frac{{{{h}_{ * }}}}{\rho } + \operatorname{tg} \alpha } \right)\frac{{dw}}{{d\rho }}} \right],$

${{\tau }_{{rz1}}} = - \frac{{E{{h}_{ * }}}}{{(1 - {{v}^{2}})c}}\left[ {\frac{{{{d}^{2}}{{u}_{0}}}}{{d{{\rho }^{2}}}} - 2\operatorname{tg} \alpha \frac{{{{d}^{2}}w}}{{d{{\rho }^{2}}}} + \frac{1}{\rho }\frac{{d{{u}_{0}}}}{{d\rho }} - \operatorname{tg} \alpha \left( {\frac{1}{\rho } - \frac{{\operatorname{tg} \alpha }}{{{{h}_{ * }}}}} \right)\frac{{dw}}{{d\rho }} - \frac{{{{u}_{0}}}}{{{{\rho }^{2}}}}} \right],$

(6)

${{\sigma }_{{z3}}} = - \frac{{E{{h}_{ * }}}}{{6(1 - {{v}^{2}})c}}\left[ {h_{*}^{2}\frac{{{{d}^{4}}w}}{{d{{\rho }^{4}}}} + 2{{h}_{ * }}\left( {\frac{{{{h}_{ * }}}}{\rho } - 2\operatorname{tg} \alpha } \right)\frac{{{{d}^{3}}w}}{{d{{\rho }^{3}}}} - } \right.$

$\left. { - \;\left( {\frac{{h_{*}^{2}}}{{{{\rho }^{2}}}} + 5\operatorname{tg} \alpha \frac{{{{h}_{ * }}}}{\rho } - 2{{{\operatorname{tg} }}^{2}}\alpha } \right)\frac{{{{d}^{2}}w}}{{d{{\rho }^{2}}}} + \frac{1}{\rho }\left( {\frac{{{{h}_{ * }}}}{\rho } + \operatorname{tg} \alpha } \right)\frac{{dw}}{{d\rho }}} \right],$

${{\sigma }_{{z2}}} = - \frac{{E{{h}_{ * }}}}{{2(1 - {{v}^{2}})c}}\left[ {{{h}_{ * }}\frac{{{{d}^{3}}{{u}_{0}}}}{{d{{\rho }^{3}}}} - 3\operatorname{tg} \alpha {{h}_{ * }}\frac{{{{d}^{3}}w}}{{d{{\rho }^{3}}}} + \left( {2\frac{{{{h}_{ * }}}}{\rho } - \operatorname{tg} \alpha } \right)\frac{{{{d}^{2}}{{u}_{0}}}}{{d{{\rho }^{2}}}} - } \right.$

$ - \;\operatorname{tg} \alpha \left( {4\frac{{{{h}_{ * }}}}{\rho } - 5\operatorname{tg} \alpha } \right)\frac{{{{d}^{2}}w}}{{d{{\rho }^{2}}}} - \frac{1}{\rho }\left( {\frac{{{{h}_{ * }}}}{\rho } + \operatorname{tg} \alpha } \right)\frac{{d{{u}_{0}}}}{{d\rho }} + $

$\left. { + \;\operatorname{tg} \alpha \frac{1}{\rho }\left( {\frac{{{{h}_{ * }}}}{\rho } + 3\operatorname{tg} \alpha } \right)\frac{{dw}}{{d\rho }} + \frac{1}{{{{\rho }^{2}}}}\left( {\frac{{{{h}_{ * }}}}{\rho } + \operatorname{tg} \alpha } \right){{u}_{0}}} \right],$

${{\sigma }_{{z1}}} = - {{h}_{ * }}\left( {\frac{{d{{\tau }_{{rz0}}}}}{{d\rho }} + \frac{{{{\tau }_{{rz0}}}}}{\rho }} \right) + $

$ + \;\frac{{E\operatorname{tg} \alpha \;{{h}_{ * }}}}{{(1 - {{v}^{2}})c}}\left[ {\frac{{{{d}^{2}}{{u}_{0}}}}{{d{{\rho }^{2}}}} - 2\operatorname{tg} \alpha \frac{{{{d}^{2}}w}}{{d{{\rho }^{2}}}} + \frac{1}{\rho }\frac{{d{{u}_{0}}}}{{d\rho }} - \operatorname{tg} \alpha \left( {\frac{1}{\rho } - \frac{{\operatorname{tg} \alpha }}{{{{h}_{ * }}}}} \right)\frac{{dw}}{{d\rho }} - \frac{{{{u}_{0}}}}{{{{\rho }^{2}}}}} \right].$

Потребуем, чтобы напряжения, вычисляемые при помощи формул (5) и (6) удовлетворяли граничным условиям (3). Находим

${{\tau }_{{rz0}}} = - \frac{{E{{h}_{ * }}}}{{(1 - {{v}^{2}})c}}\left[ {\frac{1}{2}{{h}_{ * }}\frac{{{{d}^{3}}w}}{{d{{\rho }^{3}}}} + \frac{{{{d}^{2}}{{u}_{0}}}}{{d{{\rho }^{2}}}} + \left( {\frac{1}{2}\frac{{{{h}_{ * }}}}{\rho } - 3\operatorname{tg} \alpha } \right)\frac{{{{d}^{2}}w}}{{d{{\rho }^{2}}}} + } \right.$

$\left. { + \;\frac{1}{\rho }\frac{{d{{u}_{0}}}}{{d\rho }} - \left( {\frac{1}{2}\frac{{{{h}_{ * }}}}{{{{\rho }^{2}}}} + \frac{3}{2}\operatorname{tg} \alpha \frac{1}{\rho } - \frac{{{{{\operatorname{tg} }}^{2}}\alpha }}{{{{h}_{ * }}}}} \right)\frac{{dw}}{{d\rho }} - \frac{{{{u}_{0}}}}{{{{\rho }^{2}}}}} \right],$

(7)

$\begin{gathered} {{\sigma }_{{z0}}} = \frac{{E{{h}_{ * }}}}{{(1 - {{v}^{2}})c}}\left[ {\frac{1}{3}h_{*}^{2}\frac{{{{d}^{4}}w}}{{d{{\rho }^{4}}}} + \frac{1}{3}{{h}_{ * }}\left( {2\frac{{{{h}_{ * }}}}{\rho } - \frac{{11}}{2}\operatorname{tg} \alpha } \right)\frac{{{{d}^{3}}w}}{{d{{\rho }^{3}}}} + \frac{1}{2}{{h}_{ * }}\frac{{{{d}^{3}}{{u}_{0}}}}{{d{{\rho }^{3}}}} - } \right. \\ - \;\frac{1}{3}\left( {\frac{{h_{*}^{2}}}{{{{\rho }^{2}}}} + 8\operatorname{tg} \alpha \frac{{{{h}_{ * }}}}{{{{\rho }^{2}}}} + \frac{{23}}{2}\frac{{{{{\operatorname{tg} }}^{2}}\alpha }}{\rho }} \right)\frac{{{{d}^{2}}w}}{{d{{\rho }^{2}}}} + \left( {\frac{{{{h}_{ * }}}}{\rho } + \frac{1}{2}\operatorname{tg} \alpha } \right)\frac{{{{d}^{2}}{{u}_{0}}}}{{d{{\rho }^{2}}}} + \\ \end{gathered} $

$ + \;\frac{1}{3}\left( {\frac{{h_{*}^{2}}}{{{{\rho }^{3}}}} + \frac{1}{2}\operatorname{tg} \alpha \frac{{{{h}_{ * }}}}{{{{\rho }^{2}}}} - \frac{1}{2}\frac{{{{{\operatorname{tg} }}^{2}}\alpha }}{\rho } + 3\frac{{{{{\operatorname{tg} }}^{3}}\alpha }}{{{{h}_{ * }}}}} \right)\frac{{dw}}{{d\rho }} - $

$\left. { - \;\frac{1}{{2\rho }}\left( {\frac{{{{h}_{ * }}}}{\rho } - \operatorname{tg} \alpha } \right)\frac{{d{{u}_{0}}}}{{d\rho }} - \frac{1}{{2{{\rho }^{2}}}}\left( {\frac{{{{h}_{ * }}}}{\rho } - \operatorname{tg} \alpha } \right){{u}_{0}}} \right]$

и систему основных дифференциальных уравнений задачи в перемещениях

${{h}_{*}}\frac{{{{d}^{2}}{{u}_{0}}}}{{d{{\rho }^{2}}}} + \left( {\frac{{{{h}_{*}}}}{\rho } - \operatorname{tg} \alpha } \right)\frac{{d{{u}_{0}}}}{{d\rho }} - \frac{1}{\rho }\left( {\frac{{{{h}_{*}}}}{\rho } - \nu \operatorname{tg} \alpha } \right){{u}_{0}} - \operatorname{tg} \alpha {{h}_{*}}\frac{{{{d}^{2}}w}}{{d{{\rho }^{2}}}} - $

$ - \;\operatorname{tg} \alpha \left( {\left( {1 - \nu } \right)\frac{{{{h}_{*}}}}{\rho } - \operatorname{tg} \alpha } \right)\frac{{dw}}{{d\rho }} - \frac{{1 - {{\nu }^{2}}}}{E}\operatorname{tg} \alpha cq = 0,$

(8)

$h_{*}^{3}\frac{{{{d}^{4}}w}}{{d{{\rho }^{4}}}} + 2h_{*}^{2}\left( {\frac{{{{h}_{*}}}}{\rho } - 5\operatorname{tg} \alpha } \right)\frac{{{{d}^{3}}w}}{{d{{\rho }^{3}}}} - {{h}_{*}}\left( {\frac{{h_{*}^{2}}}{{{{\rho }^{2}}}} + 14\operatorname{tg} \alpha \frac{{{{h}_{*}}}}{{{{\rho }^{2}}}} - 8{{{\operatorname{tg} }}^{2}}\alpha } \right)\frac{{{{d}^{2}}w}}{{d{{\rho }^{2}}}} + $

$ + \;\left( {\frac{{h_{*}^{2}}}{{{{\rho }^{3}}}} + 2\operatorname{tg} \alpha \frac{{h_{*}^{2}}}{{{{\rho }^{2}}}} + 10{{{\operatorname{tg} }}^{2}}\alpha \frac{{{{h}_{*}}}}{\rho } - 3{{{\operatorname{tg} }}^{3}}\alpha } \right)\frac{{dw}}{{d\rho }} + 3h_{*}^{2}\frac{{{{d}^{3}}{{u}_{0}}}}{{d{{\rho }^{3}}}} + $

$ + \;6{{h}_{*}}\left( {\frac{{{{h}_{*}}}}{\rho } - \operatorname{tg} \alpha } \right)\frac{{{{d}^{2}}{{u}_{0}}}}{{d{{\rho }^{2}}}} - 3\frac{{{{h}_{*}}}}{\rho }\left( {\frac{{{{h}_{*}}}}{\rho } + 2\operatorname{tg} \alpha } \right)\frac{{d{{u}_{0}}}}{{d\rho }} + 3\frac{{{{h}_{*}}}}{{{{\rho }^{2}}}}\left( {\frac{{{{h}_{*}}}}{\rho } + 2\operatorname{tg} \alpha } \right){{u}_{0}} + \frac{{3(1 - {{\nu }^{2}})}}{{2E}}cq = 0.$

Из анализа формул (5)–(8) видно, что в случае пластинки переменной толщины изгиб и растяжение не отделяются друг от друга.

Покажем, что напряжения, соответствующие общему интегралу уравнений дают следующие усилия и моменты:

${{N}_{r}} = \frac{{2E{{h}_{ * }}}}{{1 - {{v}^{2}}}}\left( {\frac{{d{{u}_{0}}}}{{d\rho }} + v\frac{{{{u}_{0}}}}{\rho } - \operatorname{tg} \alpha \frac{{dw}}{{d\rho }}} \right),\quad {{N}_{\theta }} = \frac{{2E{{h}_{ * }}}}{{1 - {{v}^{2}}}}\left[ {\frac{{{{u}_{0}}}}{\rho } - v\left( {\frac{{d{{u}_{0}}}}{{d\rho }} - \operatorname{tg} \alpha \frac{{dw}}{{d\rho }}} \right)} \right],$

$\begin{gathered} {{M}_{r}} = - \frac{{{{D}_{ * }}}}{{{{c}^{2}}}}\left[ {\frac{{{{d}^{2}}w}}{{d{{\rho }^{2}}}} + \left( {\frac{v}{\rho } - \frac{{\operatorname{tg} \left( \alpha \right)}}{{{{h}_{ * }}}}} \right)\frac{{dw}}{{d\rho }}} \right],\quad {{M}_{\theta }} = - \frac{{v{{D}_{ * }}}}{{{{c}^{2}}}}\left[ {\frac{{{{d}^{2}}w}}{{d{{\rho }^{2}}}} + \left( {\frac{1}{{v\rho }} - \frac{{\operatorname{tg} \alpha }}{{{{h}_{ * }}}}} \right)\frac{{dw}}{{d\rho }}} \right], \\ {{Q}_{r}} = - \frac{{{{D}_{ * }}}}{{{{c}^{3}}}}\left[ {\frac{{{{d}^{3}}w}}{{d{{\rho }^{3}}}} + \left( {\frac{1}{\rho } - 8\frac{{\operatorname{tg} \alpha }}{{{{h}_{ * }}}}} \right)\frac{{{{d}^{2}}w}}{{d{{\rho }^{2}}}} - \left( {\frac{1}{{{{\rho }^{2}}}} + 4\frac{{\operatorname{tg} \alpha }}{{{{h}_{ * }}\rho }} - 3\frac{{{{{\operatorname{tg} }}^{2}}\alpha }}{{h_{*}^{2}}}} \right)\frac{{dw}}{{d\rho }} + } \right. \\ \end{gathered} $

$\left. { + \;\frac{3}{{{{h}_{ * }}}}\frac{{{{d}^{2}}{{u}_{0}}}}{{d{{\rho }^{2}}}} + \frac{3}{{{{h}_{ * }}\rho }}\frac{{d{{u}_{0}}}}{{d\rho }} - 3\frac{{{{u}_{0}}}}{{{{h}_{ * }}\rho }}} \right],$

где ${{D}_{ * }} = \frac{{2Eh_{*}^{3}}}{{3(1 - {{v}^{2}})}}$.

Сформулируем граничные условия для определения произвольных интегрирования системы (8) следующего вида: по жестко защемленному контуру

(9)

${{u}_{0}} = w = \frac{{dw}}{{d\rho }} = 0$

и на внутреннем контуре отверстия

(10)

${{N}_{r}} = N,\quad {{M}_{r}} = M,\quad {{Q}_{r}} = P.$

При других вариантах закрепления пластинки граничные условия будут представлять собой комбинацию условий (9) и (10).

Анализируя уравнения (8) можно установить, что построенная модель определения НДС во внутренней области круглой пластинки с несимметрично изменяющейся толщиной базируется на гипотезе о неизменяемости вертикального элемента, т.е. отрезка прямой, перпендикулярного нижней грани пластинки. Эта гипотеза является обобщением известных гипотез Кирхгофа–Лява о неизменяемости нормального к серединной плоскости пластинки элемента.

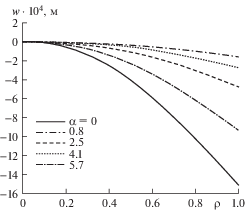
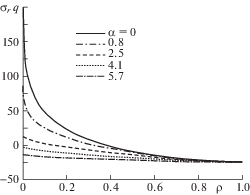
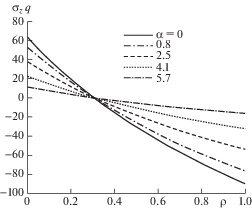
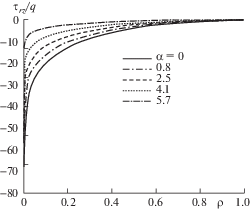
Пример расчета. Рассмотрим круглую пластинку с центральным отверстием, находящуюся под действием распределенной по верхнему основанию нагрузки. Расчеты проведены в системе “Matlab-14” методом конечных разностей. На рис. 2–5 приведены эпюры прогиба w и компонентов НДС по радиусу пластинки в зависимости от угла α, где точка ρ = 0 соответствует жестко защемленному краю, а точка ρ = 1 – внутреннему контуру пластинки. Значение угла α = 0 соответствует пластинке постоянной толщины, что позволяет провести соответствующие сравнения с пластинкой переменной толщины.

Рис. 2.

Рис. 3.

Эпюры прогиба W (рис. 2) и нормального напряжения σ_r (рис. 3), где α в град.

Рис. 4.

Рис. 5.

Эпюры нормального напряжения σ_θ (рис. 4) и касательного τ_rz (рис. 5) напряжения, где α в град.

Анализ рис. 2–5 показывает, что при наличии незначительной переменности толщины, например, α = 0.8°, поперечная жесткость на краю пластинки увеличивается на 60% по отношению к пластинке постоянной толщины. Дополнительные расчеты с использованием полученных результатов позволяют установить, что при этом же значении угла α прочность на краю пластинки можно повысить примерно в 2 раза, уменьшив массу пластинки на 30%.

Следует отметить, что к построенному основному НДС круглой пластинки необходимо добавить НДС типа “погранслой”, возникающий вблизи жестко защемленного края. В результате полное НДС рассматриваемой пластинки будет определено с точностью относительной толщины в каждой ее точке.

Работа выполнена при финансовой поддержке РФФИ (грант № 17-08-00849а).

Список литературы

Гольденвейзер А.Л. Теория упругих тонких оболочек. М.: Наука, 1976. 512 с.

Фирсанов В.В. Об уточнении классической теории прямоугольных пластинок из композиционных материалов // Механика композиционных материалов и конструкций. 2002. Т. 8. № 1. С. 28–64.

Фирсанов В.В. Исследование напряженно-деформированного состояния прямоугольных пластинок на основе неклассической теории // Проблемы машиностроения и надежности машин. 2016. № 6. С. 35–43.

Фирсанов В.В. Напряженное состояние типа “пограничный слой” – краевое кручение прямоугольной пластинки // Строительная механика инженерных конструкций и сооружений. 2016. № 6. С. 44–51.

Фирсанов В.В. Математическая модель напряженно-деформированного состояния прямоугольной пластинки переменной толщины с учетом пограничного слоя // Механика композиционных материалов и конструкций. 2016. Т. 22. № 1. С. 3–18. (МРБД Chemical Abstracts).

Тимошенко С.П., Войновский-Кригер С. Пластинки и оболочки. М.: Наука, 1966. 635 с.

Фирсанов В.В., Доан Ч.Н. Энергетически согласованная теория цилиндрических оболочек // Проблемы машиностроения и надежности машин. 2011. № 6. С. 49–54.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал