Проблемы машиностроения и надежности машин, 2019, № 1, стр. 3-14

Известно явление отрыва жидкости от твердых поверхностей при их резком движении в направлении по нормали. Это происходит в результате снижения давления на контактной поверхности. Теоретическому и экспериментальному изучению различных аспектов кавитации жидкостей посвящена обширная литература (например, [1–5]). Значительное внимание уделено анализу взаимодействия ударной волны в жидкости и деформации тонкостенных элементов конструкций. В частности, в [6, 7] экспериментально и теоретически изучено кавитационное взаимодействие падающей ударной волны с тонкостенной пластиной, представляющей днище вертикальной трубы. Показано, что в случае тонкой пластины на ее поверхности образуется кавитационная полость, что приводит к сильному изменению картины взаимодействия. В случае достаточно толстой пластины кавитация не возникает. Эти исследования направлены на определение напряженно-деформированного состояния и устойчивости элементов конструкций, контактирующих с жидкостью, гидродинамической штамповки тонкостенных деталей т.д.

Роль кавитационных явлений в различных технологических операциях, например, измельчения различных сред, их смешивания и очистки поверхностей рассмотрена в [8, 9], где изучено применение этих явлений в космических технологиях. В экспериментах по возбуждению вертикальных колебаний прозрачного цилиндрического сосуда с водой выявлены разные режимы образования кластера пузырьков, их миграции, группирования в зависимости от отношения собственных частот и частоты возбуждения.

Вопросы достижения высоких параметров в кластере кавитационных пузырьков рассмотрены в [10] и других работах. Большое число исследований посвящено анализу кавитационного обтекания препятствий потоком жидкости [11–13], рассмотрены различные аспекты воздействия кавитационных пузырьков на стенки каналов [14], где ценными являются экспериментальные результаты.

Настоящее исследование посвящено качественному аналитическому моделированию образования и схлопывания кавитационной полости и сравнению с экспериментальными данными, полученными в [15, 16], где описано, как вертикальная стеклянная бутылка с водой подвергается сверху удару, что приводит к образованию развитой кавитационной полости у днища. Затем в результате резкого повышения давления при ее схлопывании происходит разрушение бутылки.

Известно [3], что число кавитации Са определяется равенством

где L, ρ – высота столба жидкости и ее плотность; р₀, ${{р }_{v}}$ – давления на верхнюю и нижнюю поверхности (р₀ – атмосферное давление, ${{р }_{v}}$ – давление насыщенных паров); g, $\ddot {u}$ – гравитационное и наведенное ускорения.

Будем исходить из предположения $\ddot {u} > g$. В экспериментах [15, 16] показано, что Са ≤ 0.6. Эти данные будем использовать при построении модели явления.

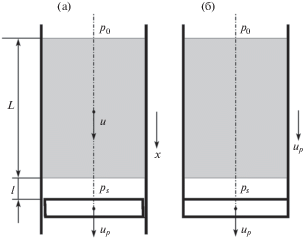
1. Простейшая модель образования кавитационной полости и ее схлопывания. Столб идеальной несжимаемой жидкости плотностью ρ, высотой L в вертикальной трубе удерживается в равновесии поршнем или днищем трубы (рис. 1). На верхнюю поверхность действует атмосферное давление р₀, на нижнюю – давление р_s = р₀ + gρL. В момент времени t = 0 поршень приходит в движение в направлении вниз по заданному закону

Коэффициенты ряда а₀, а₁ равны нулю в силу равенства нулю перемещения и скорости при t = 0. Предполагаем, что продолжительность t_р перемещения поршня имеет порядок действия ударных волн в жидкостях 10^–3 с [2–7]. Ускорение этого движения в начальный момент значительно превосходит гравитационное ускорение g. Возможно изменение знака в интервале 0 < t ≤ t_р. Принимаем, что высота столба L имеет порядок 10^–1 м, так что при скорости волны с = 1500 м/с время прохождения ее по длине L имеет порядок L/с ∼ 10^–4 с. Следовательно, за время движения поршня происходит многократное отражение волны от концов столба. Тогда приближенно можно не учитывать растяжение–сжатие столба жидкости за это время (за исключением начального и конечного моментов движения).

В интервале времени 0 < t ≤ ${{t}_{v}}$ происходит совместное движение поршня и столба жидкости, когда давление на контактной поверхности падает от значения р_s = р₀+ gρL до давления насыщенных паров ${{p}_{v}}$. Поэтому в уравнении движения жидкости $\rho L\ddot {u}$ = = ${{p}_{0}} + g\rho L - {{p}_{s}}$ для этого интервала времени вместо $\rho L\ddot {u}$ примем $\rho L{{\ddot {u}}_{p}}\alpha $ (точка над буквой – производная по времени t). Величина α < 1 и зависит от продольной координаты и времени. Введение ее позволяет приближенно учитывать начальное растяжение жидкого слоя и уменьшение средней плотности вблизи поверхности поршня в результате расширения мельчайших пузырьков при падении давления.

В настоящем приближенном анализе величину α считаем постоянной, определяемой исходя из экспериментальных данных. При этом вводим в рассмотрение тонкий однородный кавитационный слой на поверхности поршня толщиной l(t) = u_p(t) – u(t) = = (1 – α)u_p, оставляя неизменной массу ρL жидкости на единицу площади поперечного сечения.

Момент ${{t}_{v}}$ отрыва жидкости от поршня определяем из условия р_s = ${{p}_{v}}$ или

где ${{\ddot {u}}_{p}}({{t}_{v}})$ – заданное ускорение поршня в момент ${{t}_{v}}$. При α = Са уравнение (3) совпадает с (1), однако величина α имеет более широкий смысл.

В соответствии с (2) ${{\ddot {u}}_{p}}({{t}_{v}}) = 2{{a}_{2}} + 6{{a}_{3}}{{t}_{v}} + 12{{a}_{4}}t_{v}^{2}$. С учетом этого из (3) находим

Знак перед корнем в (4) определяется с учетом знаков а₂, а₃, а₄. Если известно значение ${{р }_{v}}$, то коэффициент α определяется по формуле (3).

В интервале ${{t}_{v}}$ < t ≤ t_m движение столба жидкости определяется уравнением $\ddot {u} = P$ при условиях $u = \alpha {{u}_{p}}$, $\dot {u} = \alpha {{\dot {u}}_{p}}$ в момент t = ${{t}_{v}}$. Решение этого уравнения с этими условиями имеет вид

где t_m – момент достижения максимальной толщины кавитационного слоя l = u_p – u. Он определяется из условия $\dot {l} = 0$ или ${{\dot {u}}_{p}}({{t}_{m}}) = \dot {u}({{t}_{m}})$. Подставив сюда выражения (2) и (5) получаем уравнение относительно t_m

При определении корней уравнения (6) отбросим последние два члена. Их вклад будет оценен далее при задании конкретных данных. Тогда решение уравнения (6) имеет вид

Знак перед вторым членом в скобках определяем при рассмотрении конкретных данных. Выражения $u({{t}_{m}})$ и $\dot {u}({{t}_{m}})$ получаем из (5)

Рассмотрим движение в интервале t_m < t ≤ t_с, где t_с – момент схлопывания кавитационного слоя. При t = t_с толщина этого слоя l(t_с) = u_p(t_с) – u(t_с) = 0. Из этого уравнения определяем значение t_с. Принимаем предположение, что оно меньше или равно времени заданного движения поршня (t_с ≤ t_р) и в интервале t_m < t ≤ t_с происходит адиабатическое сжатие кавитационного слоя с показателем γ. Тогда уравнение движения принимает вид

Решение уравнения (9) ищем в виде

где ${{u}_{0}} = u({{t}_{m}})$, ${{u}_{1}} = \dot {u}({{t}_{m}})$, причем $u({{t}_{m}})$ и $\dot {u}({{t}_{m}})$ определены в (8). Кроме того в (2) теперь ${{a}_{0}} = {{u}_{p}}({{t}_{m}})$, ${{a}_{1}} = {{\dot {u}}_{p}}({{t}_{m}})$. Коэффициенты а₂, а₃, а₄ сохраняют свои значения. Тогда

В (9) и (11) используем приближение (1 + z)^–γ = 1 – γz + γ(γ + 1)z²/2. Подставляя (10) и (11) в уравнение (9) и сравнивая члены при одинаковых степенях τ, находим коэффициенты (10)

Возрастание давления в кавитационной полости в интервале t_m < t ≤ t_с определяется по формуле

сюда нужно подставить выражения (11), (12).

2. Кавитация при движении поршня с постоянным ускорением. Принимаем, что ускорение поршня скачкообразно возрастает при t = 0, затем скачкообразно обращается в нуль при t = t_р. Из (2) следует

В рамках модели в данном случае время ${{t}_{v}}$ = 0, коэффициент α не вводится. Таким образом, кавитация жидкости возникает сразу в начале движения поршня. Так как теперь ${{u}_{p}}({{t}_{v}}) = {{u}_{p}}(0) = 0$, ${{\dot {u}}_{p}}({{t}_{\text{v}}}) = {{\dot {u}}_{p}}(0) = 0$, то по (5) перемещение нижней поверхности столба жидкости равно

Уравнения (6), (7), а также время максимальной толщины кавитационного слоя t_m не имеют места, так как происходит постоянное увеличение величины l(t) = u_p(t) – u(t) в пределах 0 ≤ t ≤ t_р. В момент t_р движение поршня прекращается, достигается максимальная толщина слоя l(t_р) = u_p(t_р) – u(t_р), где в соответствии с (14), (15) имеем u_p(t_р) = = ${{a}_{2}}t_{p}^{2}$, u_p(t_р) = Р$t_{p}^{2}{\text{/}}2$. Поэтому можно считать, что t_m = t_р = 5 · 10^–3 с. При t = t_р скорость столба жидкости $\dot {u}({{t}_{p}}) = P{{t}_{p}}$, а скорость поршня ${{\dot {u}}_{p}}({{t}_{p}}) = 0$. Следовательно, $\dot {l}({{t}_{p}})$ = –Pt_p. Дальнейшее движение столба жидкости определяется уравнением (9), где вместо l(t_m) нужно подставить l(t_р). По (10)

Так как ${{\dot {u}}_{p}}({{t}_{p}}) = 0$, то $\dot {l}({{t}_{p}}) = {{\dot {u}}_{p}}({{t}_{p}}) - \dot {u}({{t}_{p}}) = - \dot {u}({{t}_{p}})$. В рассматриваемом случае а₃ = = а₄ = 0, поэтому вместо (11) имеем

Используя для (17) разложение функции (1 + z)^–γ в степенной ряд и с учетом (16) из уравнения (9) находим коэффициенты ряда

Оценим члены ряда (16), (18) при следующих данных. Примем высоту столбика воды L = 0.15 м, значения плотности ρ = 10³ кг/м³, ускорения g = 9.81 м/с², давлений р₀ = = 1 бар = 10⁵ кг/(м · с²), ${{p}_{v}}$ = 0.022 бар, показателя адиабаты γ = 1.325, а₂ = 2940 м/с², t_р = 5 · 10^–3 с. В соответствии с (3) Р = 750 м/с². К моменту t_р остановки поршня толщина кавитационного слоя равна

С учетом приведенных значений $u({{t}_{p}}) = Pt_{p}^{2}{\text{/}}2$, ${{\dot {u}}_{p}}({{t}_{p}}) = P{{t}_{p}}$, а также выражений (18) ряд (16) приводим к виду

Если наибольшее значение τ = τ_с= t_с – t_р принять равным 2t_р = 10^–2 с, то из (20) получаем и = (3375 – 91 – 15)$t_{p}^{2}$.

Таким образом, ряд (16) или (20) быстро сходится. Основными являются первые члены, пропорциональные τ². Это означает, что движение столба жидкости до удара по уже остановившемуся поршню (в момент t_р) происходит без заметного противодействия со стороны сжимающегося кавитационного слоя. Ввиду такой сходимости момент схлопывания слоя t_с можно определить из условия l(t_с) = и(t_с) – и_р(t_р) = 0 с учетом только первых трех членов (16) или первого члена (20). Итак $Pt_{c}^{2} - 2{{a}_{2}}t_{p}^{2} \approx 0$, отсюда

При принятых данных из (21) следует t_с = 2.8t_р или τ_с= t_с – t_р = 1.8t_р. Это свидетельствует, что приведенная оценка сходимости ряда (16) с принятым значением τ_с = 2t_р является справедливой. Для принятых данных все движение продолжается в течение t_с = 2.8t_р = 2.8 · 5 · 10 ^–3= 14 · 10 ^–3 с, из них 9 · 10^–3 с после остановки поршня. Давление при таком сжатии кавитационного слоя определяется по (13), где вместо времени t_m должно быть t_р. При l(t_р)/l(t) = 20 давление в слое равно р = 1.16 бар, при l(t_р)/l(t) = 100 давление р = 9.83 бар. Процесс самого удара столбиком жидкости по поршню исключается из данного рассмотрения.

3. Сравнение с экспериментальными данными. В [15, 16] приводятся результаты экспериментального исследования кавитации в вертикальной стеклянной бутылке с водой. Эксперимент соответствует правой схеме на рис. 1. По кромке горлышка открытой бутылки, удерживаемой экспериментатором за боковую стенку, производится удар. Стенка и днище бутылки получают ускоренное движение, направленное вниз. Столбик воды отстает от движения днища, в результате чего происходит его отрыв от днища. Образованная при этом полость заполняется пузырьками, примыкающими друг к другу (рис. 2). В дальнейшем происходит сжатие полости, в результате чего возрастает давление в этом пароводяном объеме. Резкое повышение давления при схлопывании полости и удар столбика воды по днищу приводят к образованию трещин и разрушению бутылки.

На рис. 3 приводится запись показаний датчика ускорений, прикрепленного к нижней поверхности днища. На рис. 2 и 3 отсчет времени t начинается с момента удара по верхней кромке бутылки, поэтому начало показания датчика на днище соответствует времени t₀ ≈ 0.5 мс. В приведенных формулах отсчет времени начинается с момента записи датчика. В отличие от эксперимента в расчетах положительное направление ускорения принято вниз.

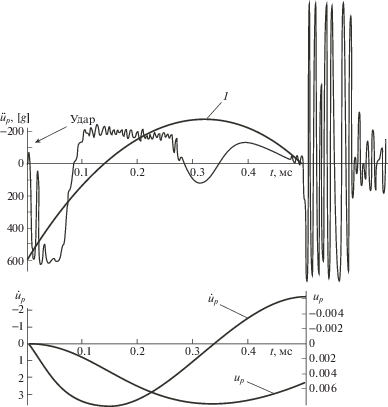
Если ограничиться представлением (1) перемещения поршня (днища), то его ускорение ${{\ddot {u}}_{p}} = 2{{a}_{2}} + 6{{a}_{3}}t + 12{{a}_{4}}{{t}^{2}}$, где для записи ускорений на рис. 3 приближенно а₂ = = 2940 м/с², а₃ = –9 · 10⁵ м/с³, а₄ = 7 · 10⁷ м/с⁴. Соответствующая кривая показана на рис. 3 цифрой 1. При рассмотрении скачкообразного увеличения ускорения на величину 2а₂ в разделе 2 специально было взято значение а₂. В нижней части рис. 3 приведены эпюры скорости ${{\dot {u}}_{p}}(t)$ и перемещения ${{u}_{p}}(t)$. Сравнение эксперимента и теории будем проводить до начала процесса разрушения. Из рис. 3 следует, что это время равно 5–5.5 мс, хотя оно не совсем совпадает с рис. 2, где при t = t₁₂ – 0.5 = 5.22 мс кавитационная полость еще не сжалась. Возможно, что данные по рис. 2 и 3 соответствуют разным экспериментам.

Значение Р по (3) для данного эксперимента мало зависит от последних двух членов и равно Р ≈ р₀/(ρL) = 750 м/с². Время ${{t}_{\text{v}}}$ достижения давления ${{p}_{v}}$ на контактной поверхности определяется по (4). Из рис. 2 видно, что это время соответствует промежутку между кадрами, обозначенными t₆ и t₇. Примем это время равным 1 мс, что с учетом сдвига t в расчетах дает ${{t}_{\text{v}}}$ = 0.5 мс. Тогда по (4) или из выражения

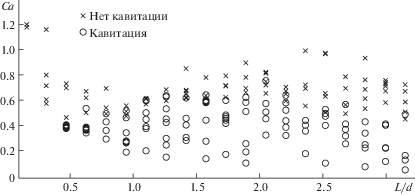
Если принять ${{t}_{v}}$ = 0.8 мс, то по (22) имеем α = 0.36. Коэффициент α может быть определен по рис. 4 [16], где представлены экспериментальные данные по числу кавитации Са и относительной высоте L/d (d – диаметр бутылки). Видна слабая зависимость числа Са от L/d. Наибольшее количество значений Са, когда возникает кавитация, находится примерно в пределах 0.2 < Са < 0.6. Число Са и коэффициент α можно отождествить. Найденные значения α = 0.22 и α = 0.36 находятся в интервале приведенных значений Са. В дальнейшем будем применять значение α = 0.22 (${{t}_{v}}$ = 0.5 мс).

Перемещение и скорость поршня в момент ${{t}_{v}}$ = 0.5 мс в соответствии с (2) равны ${{u}_{p}}({{t}_{v}})$ = 0.62 · 10^–3 м, ${{\dot {u}}_{p}}({{t}_{v}})$ = 2.30 м/с. Следовательно, $u({{t}_{v}}) = \alpha {{u}_{p}}({{t}_{v}})$ = 0.13 · 10^–3 м, $\dot {u}({{t}_{v}})$ = $\alpha {{\dot {u}}_{p}}({{t}_{v}})$ = 0.51 м/с, а приведенная толщина кавитационного слоя l(${{t}_{v}}$) = и_р(${{t}_{v}}$) – – и(${{t}_{v}}$) = 0.49 ⋅ 10^–3 м. По (5) и полученным числовым данным ${{u}_{p}}({{t}_{v}})$, ${{\dot {u}}_{p}}({{t}_{v}})$, Р и α функция перемещения определяется в интервале ${{t}_{v}}$ < t < t_m.

По (7) определяем время t_m наибольшей толщины кавитационного слоя. Корни его равны t_m = 2.68 мс, t_m = 7.0 мс. Второй из них лежит выше рассматриваемого интервала времени, поэтому принимаем первый корень. Он несколько меньше, чем в эксперименте (на рис. 3 это время обозначено t₃ ≈ 3.6, что соответствует расчетному времени 3.6 – 0.5 = 3.1 мс).

Оценим влияние отброшенных членов $P{{t}_{v}} - {{\dot {u}}_{p}}({{t}_{v}})$ = 0.264 м/с в уравнении (6) при определении его корней по (7). Таким образом, невязка уравнения (6) составляет Δ = = 0.264. Требование Δ = 0 приводит к изменению результата t_m = 2.68 мс только в третьем знаке после запятой.

В этот момент перемещение поршня по (2) при найденных значениях а₂, а₃, а₄ равно и_р(2.68) = 7.39 · 10^–3 м, а перемещение столба жидкости по (10), (12) равно и(2.68) = = 3.02 · 10^–3 м. Поэтому толщина слоя каверны l(2.68) = и_р(2.68) – и(2.68) = 4.37 · 10^–3 м. В [15, 16] не приводятся данные о внутреннем диаметре d бутылки и максимальной толщине слоя l. Если принять d = 0.05 м и по рис. 2 отношение l/d примерно 1/5, то l ≈ 0.01 м. Таким образом, наблюдаемая в эксперименте толщина l около двух раз больше, чем найденная по расчету. Здесь следует принять во внимание некоторое несоответствие рис. 2 и 3. Кроме того в простейшей модели предполагается чисто паровой слой, в то время как в действительности имеется пузырьковый слой с некоторой долей жидкости между пузырьками (рис. 2). Поэтому чисто паровой объем меньше, чем слой на рис. 2. Это обстоятельство сближает экспериментальные и расчетные результаты по толщине кавитационного слоя.

Для моментов времени t > t_m значение давления в кавитационной полости ${{p}_{v}}$ = = 0.022 бар, γ = 1.325 и отношениях l(t_m)/l(t) = 10 и 50 равно соответственно р = = ${{p}_{v}}$[l(t_m)/l(t)]^γ = 0.46 бар и 3.92 бар.

4. Качественный анализ процесса после удара столба жидкости. Колебания ускорений с большой амплитудой после момента t_с = 5 мс (рис. 3) можно объяснить упругими колебаниями днища в результате резкого повышения давления в исчезающем кавитационном слое и удара, а прекращение их связано с интенсивным растрескиванием стекла (последний кадр на рис. 2) и разрушением. Частота этих свободных колебаний составляет около 10⁴ Герц (10 циклов за 1 мс).

Низшая собственная частота осесимметричных колебаний круглой пластины с шарнирным закреплением краев, представляющей днище трубы, равна [17]

где Е, μ – модуль упругости и коэффициент Пуассона; d, h – диаметр и толщина пластины. Приведенная масса m единичной площади состоит из соответствующей массы пластины ρh, массы датчика ускорений и присоединенной массы жидкости, которая зависит от самой искомой частоты [17]. В целях приближенных оценок примем, что масса датчика (значение которой не сообщается в [15, 16]) равна половине массы днища и равномерно распределена по его площади, а присоединенная масса жидкости равна этой сумме. Поэтому m = 3ρh. Частота (23) пропорциональна d^–2, m^–1/2, поэтому результат не сильно зависит от неточности m.

При данных для стекла Е = 9 · 10¹⁰ кг/(м · с²), μ = 0.3, ρ = 3 · 10³ кг/м³, а также размерах днища d = 0.05 м, h = 0.005 м из (23) получаем  f  ≈ 0.73 · 10⁴ Гц, что меньше, чем экспериментальное значение. В случае принятия условий защемления края круглой пластины в (23) вместо коэффициента 3.67 будет 6.58, поэтому f ≈ 1.31 · 10⁴ Гц. Первая из этих частот является оценкой снизу, вторая – сверху. Экспериментальное значение ее лежит между ними.

Обозначим функцию прогиба днища через w(r, t). В центре r = 0 прогиб равен перемещению и_р(t), которое до рассмотрения изгибной деформации днища считалось независимой от радиуса (абсолютно жесткий поршень). Если принять условия при r = R упругой круглой пластины приближенно соответствующими шарнирному закреплению

то при $v$ → 0 функцию w можно задать в виде функции Бесселя нулевого порядка J₀(z) c аргументом z = 4.8 r/d [17].

В уравнении осесимметричного динамического изгиба круглой пластины

р_s – давление на контактной поверхности жидкости и днища, зависящее от радиуса r ввиду его изгиба. В приближенном анализе считаем р_s постоянным по всей контактной площади. Амплитуду $\ddot {W}$ колебаний ускорения $\ddot {w}(r)$ днища на стадии t > 5 мс (рис. 3) примем равной 7000 м/с². Тогда

Так как при t = t_с прогиб и скорость прогиба равны нулю, то из (25) получаем

Уравнение метода Бубнова–Галеркина по (24)–(26) будет

В приближенном анализе этой стадии движения давление р_s – р₀ не учитывается. Инерционное воздействие за счет массы днища, датчика ускорений, а также присоединенной массы жидкости учитывается вторым членом в левой части уравнения. За время полупериода колебаний около 0.05 мс не происходит отрыва жидкости от поверхности днища, так как ранее было показано ${{t}_{v}}$ ≈ 0.5 мс, поэтому прилегающий слой жидкости совершает колебания вместе с днищем.

Максимальные напряжения возникают в центре днища (r = 0). Изгибающий момент равен М = D∂²w/∂r². Вблизи центра выражение (26) можно записать

Тогда амплитуда изгибающего момента в центре равна M ≈ $0.29D\ddot {W}{\text{/}}{{(fd)}^{2}}$. При принятых ранее данных М = 8.37 кг · м/с². Напряжения на поверхностях днища при r = 0 равны σ = 6 М/h² или $\sigma = \frac{{1.74D\ddot {W}}}{{{{{(fdh)}}^{2}}}}$ ≈ 20 бар. Этот уровень напряжений на два порядка меньше, чем предел прочности стекол. Необходимо иметь в виду, что неизбежные поры в стекле, неровности и особенно микротрещины в нем являются концентраторами напряжений. Очевидно, трещины в начале развиваются вблизи этих концентраторов.

Повышение давления в жидкости приводит к разлету в разные стороны осколков боковых стенок бутылки (рис. 5 [15, 16]). Изложение характера их разлета по высоте дает некоторое представление о распространении давления вверх по жидкости. Отметим, что форма донышка в виде полусферы обеспечивает схлопывание кавитационной полости в центральной части донышка. Это приводит к разрушению главным образом этой части и к направленному потоку жидкости с осколками стекла [16].

Выводы. Приведенная простейшая модель образования кавитационной полости на контактной поверхности жидкости и ускоренно движущегося поршня в трубе предполагает одномерность задачи. Это приближение представляется приемлемым при высоте столбика, превышающей его диаметр (L/d > 1), что в экспериментах [15, 16] имеет место. Из рис. 2 видна ровная верхняя поверхность кавитационного слоя (или нижняя поверхность столба жидкости). На верхней поверхности столба одномерность движения может быть нарушена ввиду развития неустойчивости Релея–Тейлора. Однако из-за отношения L/d > 1 возмущения проникают на малую глубину по сравнению с высотой. Кроме того, направленное вниз ускорение длится менее 1 мс (рис. 3), когда развивается неустойчивость верхней поверхности жидкости, затем ускорение меняет направление, что приводит к гашению возмущений. В [15, 16] нет данных по динамике верхней поверхности жидкости.

Существенным является допущение о несжимаемости жидкости. Этот недостаток частично устраняется введением в рассмотрение расширения объема жидкости за счет роста мельчайших пузырьков при падении давления.

Из рис. 2 видно, что развитая кавитационная полость заполнена пузырьками, между которыми имеется жидкая фаза в виде пленок и малых объемов. В модели принимается однородный паровой слой толщиной, изменяющейся по времени. Максимальная расчетная толщина меньше экспериментального значения.

Процесс сжатия кавитационного слоя после достижения его максимума считается происходящим адиабатически, причем не учитывается конденсация пара, что имеет место [6]. Сильное повышение давления происходит в момент схлопывания полости, что сопровождается ударом столба по поршню (днищу бутылки). В результате этого удара по днищу возбуждаются упругие колебания, амплитуда ускорений которых в эксперименте даже больше, чем ускорение при начальном ударе по кромке горлышка бутылки (рис. 3). Частота колебаний пропорциональна величине hс/d ², где h, d – толщина и диаметр днища, с – скорость распространения волны растяжения–сжатия для стекла. В результате этих колебаний и концентрации динамических напряжений вблизи неровностей и микротрещин происходит разрушение испытуемого образца.

Приведенную модель можно уточнить при наличии новых экспериментальных результатов.

Работа выполнена частично по грантам РФФИ № 17-41-02040017-р_а, № 18-01-00150.