Проблемы машиностроения и надежности машин, 2019, № 1, стр. 53-65
МЕТОДИКА СИНТЕЗА УПРАВЛЯЮЩИХ ВОЗДЕЙСТВИЙ ДЛЯ ОБЕСПЕЧЕНИЯ ЗАДАННОГО УРОВНЯ НАДЕЖНОСТИ
В. М. Труханов 1, *, М. П. Кухтик 1
1 Волгоградский государственный технический университет
Волгоград, Россия
* E-mail: trukhanov1939@mail.ru
Поступила в редакцию 28.03.2017
Аннотация
Предлагаемая методика позволяет учесть активные управляющие воздействия, выраженные в виде конструктивных, технологических и эксплуатационных параметров, при создании технических систем. Она решает задачу управления процессом совершенствования изделия при направленном улучшении его выходной характеристики. Объектом исследования является подвижная установка специального назначения. При оценке управляющих воздействий использован математический аппарат матричного исчисления и методы математической статистики. Получены уравнения управляющих воздействий для закона распределения Вейбулла и экспоненциального закона без учета наложенных ограничений. Приведен пример нахождения управляющих воздействий.
Объектом исследования является подвижная установка специального назначения. Известно, что существующие методы достижения и обеспечения заданного уровня надежности на этапе создания требуют уточнения и соответствующей корректировки. В связи с этим поставлена задача целенаправленного изменения значений параметров конструктивного, технологического и эксплуатационного характера отдельных элементов, сборочных единиц, узлов и изделия в целом для достижения и обеспечения заданного уровня надежности и других технических и эксплуатационных характеристик.
В настоящей статье управляющие воздействия, выраженные в виде изменений конструктивных, технологических и эксплуатационных параметров, исходят от конструктора, технолога или эксплуатационника и влияют на выходную характеристику изделия в целом или ее составных частей. Полученные с помощью управляющих воздействий выходные характеристики позволят сократить время для достижения требуемого уровня надежности или другой технической и эксплуатационной характеристики.
Так как одной из важнейших характеристик для подвижных установок специального назначения является надежность выполнения поставленной задачи в заданное время в соответствии с нормативными документами, то необходимо принять в качестве выходной характеристики функцию надежности. Результаты многолетней эксплуатации (30 лет) [2] более 1000 изделий показывают, что распределение вероятности безотказной работы подвижной установки подчиняется закону распределения Вейбулла с различными значениями параметров формы кривой α.
Методика основывается на теоретических разработках и результатах исследований, проведенных в работах [1–5]. При разработке математической модели для вновь создаваемого изделия задача состоит в том, чтобы выходная характеристика этого изделия не была хуже выходной характеристики изделия–аналога после его отработки при условии изменения конструктивных, технологических и других параметров нового изделия, предназначенного для выполнения более сложных задач.
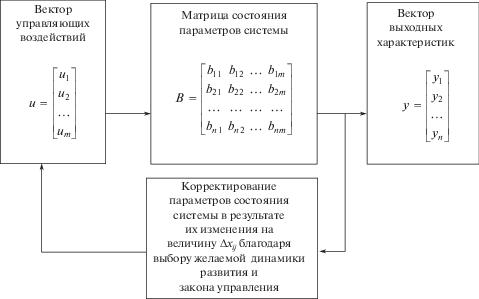
Учитывая специфику отработки сложных технических систем, рассмотрим задачу определения управляющих воздействий в явном аналитическом виде. Для решения этой задачи сделаны некоторые предпосылки. При разработке математической модели считается неизвестной модель системы, а необходимые управляющие воздействия находят, задаваясь динамикой развития системы и законом ее управления [1]. Принимая во внимание специфику рассматриваемой задачи, в математическую модель вводят новый класс желаемых законов управления и допущение об экспоненциальности (плавности) желаемой динамики развития системы. Это позволяет избежать построения нелинейных уравнений. При таком подходе к решению задачи можно получить систему линейных уравнений, обеспечивающих нахождение управляющих воздействий в явном виде. Модель отработки представим в виде системы, имеющей вход, выход и характеризуемое состояние (рис. 1).
В качестве входа в эту систему принимаем вектор управляющих воздействий, который можно представить в виде: конструктивных изменений отрабатываемых систем или элементов, заложенных в конструкторской документации; изменения технологических параметров в части ужесточения допусков на изготовляемые и контролируемые детали, узлы и другие сборочные единицы; уточнения эксплуатационной документации.
Из практики отработки сложных технических систем известно, что наибольшее влияние на выходную характеристику оказывают управляющие воздействия, связанные с конструктивными изменениями отрабатываемых систем или элементов, меньшее влияние – изменения технологических параметров и еще меньшее – уточнение эксплуатационной документации. Под конструктивным воздействием на параметры понимают изменение геометрических размеров, массовых характеристик, запаса прочности, запаса по ресурсу, изменение материала, введение резервирования элементов и т.п. Изменения технологических параметров связаны с увеличением или уменьшением допусков при изготовлении или регулировании, введением дополнительных технологических операций и так далее, а уточнение эксплуатационной документации – с внесением в инструкцию эксплуатации дополнительных указаний при ручных операциях. Например, вводят таблички с надписями “Опасно”, “Внимание”, “Выпустить воздух” и т.д.
Если в процессе отработки изделия выполняют большое число доработок и соответственно накоплен достаточно обширный статистический материал, то в этом случае целесообразно строить модель роста надежности для каждого вида управляющих воздействий – конструкционных, технологических, изменений эксплуатационной документации. Влияние каждого управляющего воздействия на выходную характеристику системы целесообразно оценить по предыстории с помощью функций регрессии, которые позволяют учесть количественные и качественные факторы. Под выходными характеристиками узлов, механизмов и изделия в целом понимают изменение основных параметров, заложенных в технических условиях на них. Такими характеристиками могут быть вероятность безотказной работы, наработка на отказ, сила выходного тока или напряжение, производительность, время подъема ракеты в вертикальное положение с подвижной установки для ее пуска и т.д.
Наиболее важной выходной характеристикой, предъявляемой к сложной технической системе, является ее работоспособность, которая чаще всего представлена в виде наработки на отказ или вероятности безотказной работы. Эти характеристики являются обобщенными, так как они определяют, в конечном итоге, выполнение поставленной перед изделием задачи. Рассмотрим случай, когда выходная характеристика выражается изменением наработки на отказ, являющийся соотношением вида
(1)
${{y}_{i}}\left( t \right) = T_{i}^{{{\text{т р }}}}\left( t \right) - {{T}_{i}}\left( t \right),$Основная задача процесса доработок состоит в том, чтобы обеспечить рост величин Ti(t) и приблизить к нулю значение функции (1). Практика отработки изделий показывает, что во многих случаях желательно иметь плавное изменение выходной характеристики. Такому изменению должно соответствовать изменение во времени решения дифференциального уравнения $dy(t){\text{/}}dt$ = –Dy. Примем
где exp(–Dt) – матричная экспонента; y0 – вектор начального состояния выходной характеристики изделия (системы). Для простоты предположим, что D – диагональная матрица, т.е.При таком выборе матрицы D из уравнения (2) следует
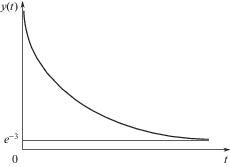
Пусть t0 – заданный срок отработки. Тогда уравнение (3) будет плавно приближаться к нулю, если коэффициенты λi = 3/t0. Изменение выходной характеристики в процессе отработки показано на рис. 2. Такое допущение позволяет предположить, что D = 3I/t0, где I – единичная матрица.
Следует отметить, что в этом случае можно было обойтись решением скалярных уравнений, так как матрица диагональная. Здесь она дана для дальнейшего обобщения, поскольку использовалась матричная экспонента для недиагональной матрицы.
Многолетняя практика отработки сложных технических систем показывает, что механизмы, пульты и другие сборочные единицы необходимо подвергать испытаниям в объеме, равном объему испытаний изделия в целом. На основании этого можно предположить, что время отработки для всех исполнительных механизмов одинаково, т.е. ti = t0. В этом случае выходная характеристика изделия упрощается и принимает вид y(t) = exp(–t/t0)y0.
Анализ (2) и (3) показывает, что эти формулы определяют заданные условия изменения выходной характеристики изделия, создаваемые правильным выбором управляющих воздействий, т.е. выбором вектора управления. На практике успех в реализации заданной программы отработки обеспечивают в результате определенных приращений вектора управления в некотором интервале, т.е. благодаря обеспечению вполне конкретных значений скоростей изменения управления. Таким образом, желаемый закон управления, к которому следует стремиться, должен содержать производную от вектора управления. Одновременно с этим, производные являются факторами, влияющими на выходную характеристику. Такой выбор желаемого закона управления позволяет упростить обработку статистических данных по методу наименьших квадратов и одновременно учесть суммарные воздействия всех управлений, действующих прямо или косвенно на суммарное изменение выходной характеристики изделия в целом.
Любую доработку осуществляют после определенного накопления факторов, вызывающих необходимость ее проведения. В количественной форме это выражается следующим образом. Если выходная характеристика изделия представляет собой центральный момент, выраженный в функции времени y(t) = Tтр(t) – T(t), по которому проводят доработку, то управляющее воздействие u(t) должно быть пропорционально интегралу на отрезке [0, t]. Эти соображения предполагают выбор формы желаемого закона управления
(4)
$Bu\left( t \right) = \int\limits_0^t {y\left( \tau \right)d\tau } \quad {\text{и л и }}\quad B\frac{{du\left( t \right)}}{{dt}} = y\left( t \right),$Такая форма записи желаемого закона управления содержит управление в неявной форме. В этом случае описывается ситуация, когда управление осуществляют по накопленному суммарному изменению выходной характеристики в форме линейной комбинации управлений. Переходя от скалярного случая к векторному, когда управление является векторной функцией времени и аналогично, выходная характеристика представляет собой вектор, имеем
Постоянная величина B в уравнении (4) является не числом, а матрицей, постоянной и определенной для некоторого одного момента времени, т.е.
Тогда уравнение (4) в развернутом виде можно записать так
Таким образом, желаемый закон управления, отображаемый уравнением (4), является уравнением неявного вида. Если в это уравнение подставить заданное значение вектора $y\left( t \right) = y_{t}^{{{\text{т р }}}}$, то полученное в результате уравнение
может не иметь решения при каждом значении t, так как в этом случае ничем не гарантируется выполнение условия являющегося необходимым и достаточным для разрешимости уравнения. В уравнении (6) B+ – матрица, псевдообратная матрице B.Для решения уравнения (5) воспользуемся методом наименьших квадратов [5], согласно которому вектор управления должен удовлетворять условию (6) наилучшим образом, т.е. сумма квадратов координат вектора $\varepsilon = y_{t}^{{{\text{т р }}}} - B(du(t){\text{/}}dt)$ должна достигнуть наименьшего значения. В соответствии с этим решение имеет вид du(t)/dt = ${{B}^{ + }}y_{t}^{{{\text{т р }}}}$.
С учетом соотношений (2) и (4) и при введении в них обозначения y0 = yтр получим [1]
Учитывая, что
(7)
$\int\limits_0^t {{\text{exp}}\left( { - D\tau } \right)y_{t}^{{{\text{т р }}}}d\tau = {{D}^{{ - 1}}}\left( {I - {\text{exp}}\left( { - Dt} \right)} \right){{y}^{{{\text{т р }}}}}} ,$(8)
$u\left( t \right) = {{u}^{{\text{0}}}} + {{B}^{ + }}{{D}^{{ - 1}}}\left( {I - {\text{exp}}\left( { - Dt} \right)} \right){{y}^{{{\text{т р }}}}}.$Преобразуем соотношения (7) и (8)
(9)
${{D}^{{ - 1}}} = {{t}_{{\text{0}}}}I{\text{/}}3,\quad (I - {\text{exp}}( - Dt)) = (1 - {\text{exp}}( - 3t{\text{/}}{{t}_{{\text{0}}}}))I,$После подстановки (9) в выражение (8) имеем
(10)
$u\left( t \right) = {{u}^{{\text{0}}}} + ({{t}_{{\text{0}}}}{\text{/}}3)(1 - {\text{exp}}( - 3t{\text{/}}{{t}_{{\text{0}}}})){{B}^{ + }}{{y}^{{{\text{т р }}}}}.$В общем виде при задании времени T отработки вектор управляющих воздействий u(t) = u0 + T(1 – exp(–t/T))B+yтр.
Развернутый вид этого вектора
(11)
$\left[ \begin{gathered} {{u}_{1}}\left( t \right) \\ ...{\text{ }}... \\ {{u}_{m}}\left( t \right) \\ \end{gathered} \right] = \left[ \begin{gathered} u_{1}^{0}\left( t \right) \\ ...{\text{ }}... \\ u_{m}^{0}\left( t \right) \\ \end{gathered} \right] + T\left( {1 - {\text{exp}}\left( { - \frac{t}{T}} \right)} \right){{\left[ {\begin{array}{*{20}{c}} {{{b}_{{11}}}}&{{{b}_{{12}}}}&{...}&{{{b}_{{1m}}}} \\ {...}&{...}&{...}&{...} \\ {{{b}_{{n1}}}}&{{{b}_{{n2}}}}&{...}&{{{b}_{{nm}}}} \end{array}} \right]}^{ + }}\left[ \begin{gathered} y_{1}^{{{\text{т р }}}} \\ ... \\ y_{n}^{{{\text{т р }}}} \\ \end{gathered} \right].$Из формулы (10) следует, что при t = 0 вектор управления u(t) = u0, а при t = t0 будет u(t) ≈ u0 + B+yтр/3.
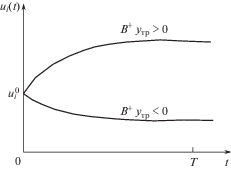
Таким образом, для изделия в целом функция управления ui(t) экспоненциально возрастает или убывает относительно значения $u_{i}^{0}$ в зависимости от того, является ли произведение i-й строки матрицы B+ на столбец положительным или отрицательным (рис. 3).
Следовательно, управляющие воздействия определены в явном виде для заданного срока отработки и требуемого значения выходной характеристики. Полученные решения удовлетворяют следующим двум условиям: они обеспечивают заданную динамику изменения выходной характеристики и являются наиболее близкими (при использовании метода наименьших квадратов) к значениям параметров желаемого закона управления.
При получении решения ограничения на управляющие воздействия не учитывались, поэтому может оказаться, что некоторые из расчетных значений параметров управления физически не реализуемы. Расчетные значения необходимо сравнить с допустимыми значениями и, если хотя бы одно из требований не выполняется, то провести корректирование желаемой динамики изменения выходной характеристики y(t) или параметров желаемого закона управления. После этого расчет повторяют до получения приемлемых значений параметров управления.
Полученное решение задачи позволяет определить оптимальные управляющие воздействия при заданной динамике изменения выходной характеристики y = φ(α, λ, t) изделия, желаемом законе управления u = φ(B, y, t) и наложении ограничений на управление u ≤ uдоп и срок отработки T ≤ Tдоп.
Рассмотренная модель позволяет определить управляющие воздействия в явном аналитическом виде при переходе от общей системы нелинейных дифференциальных уравнений к системе линейных дифференциальных уравнений, когда управление осуществляется по накопленному суммарному изменению выходной характеристики, а не по изменению по k-й производной от выходной характеристики. Следовательно, полученные параметры управления являются непрерывными функциями времени и обеспечивают заданную динамику развития выходной характеристики y(t). На практике доработки проводят в дискретные моменты времени, поэтому их можно получить как соответствующие точки на непрерывной кривой. В разработанной математической модели (11) учтена стохастическая природа исходных данных, полученных в результате статистического оценивания, при котором каждое следующее значение параметра управления получают на основании только новой поправки к полученному значению параметра, т.е. благодаря приращению значения параметра состояния на Δbij.
Излагаемая методика оценивания управляющих воздействий позволяет учесть активные управляющие воздействия при отработке систем и тем самым решает в активной постановке задачу управления процессом совершенствования изделия при направленном улучшении его характеристик. Основой методики являются описанные теоретические разработки. В качестве желаемой динамики изменения выходной характеристики (функции надежности) принят закон распределения Вейбулла, который является универсальным, так как при различных значениях параметра α распределения он превращается в другие виды распределений.
Выходная характеристика для принятого закона имеет вид [2] $y\left( t \right)$ = $P\left( t \right)$ = = $\exp ( - \lambda {{t}^{\alpha }})$. Тогда заданные условия изменения выходной характеристики в процессе отработки можно записать как решение дифференциального уравнения от функции распределения Вейбулла $F\left( t \right) = 1 - P\left( t \right)$ = $1 - {\text{exp}}( - \lambda {{t}^{\alpha }})$
(12)
$\frac{{dy\left( t \right)}}{{dt}} = f\left( t \right) = \frac{{dF\left( t \right)}}{{dt}} = \alpha \lambda {{t}^{{\alpha - 1}}}{\text{exp(}} - \lambda {{t}^{\alpha }}{\text{)}},$Эти условия должны быть обеспечены в результате выбора управляющих воздействий, т.е. выбора вектора управления u(t). Практика показывает, что успех в реализации программы отработки, заданной в виде уравнения (12), обеспечивают благодаря определенным приращениям Δu(t) вектора управления, т.е. желаемый закон управления пропорционален интегралу от изменения выходной характеристики. Следует отметить, что выбор желаемого закона управления позволяет определить необходимые параметры управления с использованием накопленного изменения выходной характеристики и одновременно учитывать суммарное воздействие всех параметров управлений, действующих прямым и косвенным образом на суммарное изменение выходной характеристики в целом.
Зависимость выходной характеристики y(t) от параметров управления определим в регрессионной форме линейным соотношением [1, 2, 4]
(где u0 – начальное значение параметра управления, T – заданный период отработки системы) или в развернутом виде(14)
$\begin{gathered} {{y}_{1}}(t) = {{b}_{{11}}}({{u}_{1}}(t) - u_{1}^{0}) + {{b}_{{12}}}({{u}_{2}}(t) - u_{2}^{0}) + \;...\; + {{b}_{{1m}}}({{u}_{m}}(t) - u_{m}^{0}), \\ ...\;...\;...\;...\;...\;...\;...\;...\;...\;...\;...\;...\;...\;...\;...\;...\;...\;...\;...\;...\;...\;... \\ {{y}_{n}}(t) = {{b}_{{n1}}}({{u}_{1}}(t) - u_{1}^{0}) + {{b}_{{n2}}}({{u}_{2}}(t) - u_{2}^{0}) + \;...\; + {{b}_{{nm}}}({{u}_{m}}(t) - u_{m}^{0}), \\ \end{gathered} $Для решения уравнения (13) необходимо ввести псевдообратную матрицу B+. Решением уравнения (13) является выражение вида [2, 4, 5]
(15)
$[u(t) - {{u}^{{\text{0}}}}] = {{B}^{ + }}y(t)\quad {\text{и л и }}\quad \left[ \begin{gathered} {{u}_{1}}(t) - u_{1}^{0} \hfill \\ ...\;...\;...\;... \hfill \\ {{u}_{m}}(t) - u_{m}^{0} \hfill \\ \end{gathered} \right] = {{\left[ {\begin{array}{*{20}{c}} {{{b}_{{11}}}}&{{{b}_{{12}}}}&{...}&{{{b}_{{1m}}}} \\ {...}&{...}&{...}&{...} \\ {{{b}_{{n1}}}}&{{{b}_{{n2}}}}&{...}&{{{b}_{{nm}}}} \end{array}} \right]}^{ + }}\left[ \begin{gathered} {{y}_{1}}(t) \\ ...\;... \\ {{y}_{n}}(t) \\ \end{gathered} \right].$Таким образом, управляющие воздействия для заданной динамики развития выходной характеристики, выраженной в форме распределения Вейбулла, находят, используя выражение
(16)
$u(t) = {{u}^{0}} + [1 - {\text{exp}}( - \lambda {{t}^{\alpha }}{\text{)}}]{{B}^{ + }}{{y}^{{{\text{т р }}}}}(t){\text{/}}\lambda ,$(17)
$\left[ \begin{gathered} {{u}_{1}}\left( t \right) \\ ...\;... \\ {{u}_{m}}\left( t \right) \\ \end{gathered} \right] = \left[ \begin{gathered} u_{1}^{0} \\ ... \\ u_{m}^{0} \\ \end{gathered} \right] + \frac{1}{\lambda }\left[ {1 - {\text{exp}}( - \lambda {{t}^{\alpha }}{\text{)}}} \right]{{\left[ {\begin{array}{*{20}{c}} {{{b}_{{11}}}}&{{{b}_{{12}}}}&{...}&{{{b}_{{1m}}}} \\ {...}&{...}&{...}&{...} \\ {{{b}_{{n1}}}}&{{{b}_{{n2}}}}&{...}&{{{b}_{{nm}}}} \end{array}} \right]}^{ + }}\left[ \begin{gathered} y_{1}^{{{\text{т р }}}}\left( t \right) \\ ...\;... \\ y_{n}^{{{\text{т р }}}}\left( t \right) \\ \end{gathered} \right].$Из формулы (16) следует, что при t = 0 вектор управления равен начальному значению параметра u(t = 0) = u0. При t → ∞ определяют u(t), используя выражение u(t → ∞) = u0 + B+yтр(t)/λ. Следовательно, функция управления uj(ti) плавно возрастает или убывает относительно значения $u_{j}^{0}$ в зависимости от того, является ли произведение i-й строки псевдообратной матрицы B+ на столбец y(t) положительным или отрицательным. При выводе формулы (16) предполагали, что матрица B и псевдообратная матрица B+ известны точно. В действительности матрица B, имеющая смысл таблицы коэффициентов регрессии (14), неизвестна и подлежит оцениванию [1, 5].
Методика оценки псевдообратной матрицы B+ сводится к следующему. На основании выбранного закона управления (в данном случае соотношение (13)) методом наименьших квадратов определяют коэффициенты регрессии bij [5].
Первый шаг. Берем первое уравнение из соотношений (14)
Второй шаг. Берем экспериментальные или расчетные данные по результатам испытаний или эксплуатации (m ≥ 10, n ≥ 5) для ${{y}_{1}}\left( t \right) = {{y}_{1}}$ и сводим в таблицу, записав уравнения (14) для каждой строки (табл. 1: табличная форма записи исходных данных первого уравнения).
Таблица 1
| у1 | ${{u}_{1}} - u_{1}^{0}$ | ${{u}_{2}} - u_{2}^{0}$ | … | ${{u}_{m}} - u_{m}^{0}$ | yij |
|---|---|---|---|---|---|
| у11 | ${{u}_{{11}}} - u_{1}^{0}$ | ${{u}_{{12}}} - u_{2}^{0}$ | … | ${{u}_{{1m}}} - u_{m}^{0}$ | $\begin{gathered} {{y}_{{11}}} = {{b}_{{11}}}({{u}_{{11}}} - u_{1}^{0}) + {{b}_{{12}}}({{u}_{{12}}} - \\ - \;u_{2}^{0}) + ... + {{b}_{{1m}}}({{u}_{{1m}}} - u_{m}^{0}) \\ \end{gathered} $ |
| … | … | … | … | … | … … … … … … … … … |
| yn1 | ${{u}_{{n1}}} - u_{1}^{0}$ | ${{u}_{{n2}}} - u_{2}^{0}$ | … | ${{u}_{{nm}}} - u_{m}^{0}$ | $\begin{gathered} {{y}_{{n1}}} = {{b}_{{11}}}({{u}_{{n1}}} - u_{1}^{0}) + {{b}_{{12}}}({{u}_{{n2}}} - \\ - \;u_{2}^{0}) + \;...\; + {{b}_{{1m}}}({{u}_{{nm}}} - u_{m}^{0}) \\ \end{gathered} $ |
Третий шаг. На основании исходных данных табл. 1. запишем
Четвертый шаг. Методом наименьших квадратов находим вектор
Далее по аналогии рассмотрим второе, третье и т.д. уравнения из соотношения (14).
В частном случае, когда выходную характеристику определяют для отрабатываемого изделия в целом, транспонированную матрицу [y]T записывают в виде вектора yT. При этом оценку псевдообратной матрицы также представляют в виде вектора ${{\hat {B}}^{ + }}$.
Если отработку всех исполнительных узлов, механизмов, пультов и других элементов изделия проводят в составе изделия, то оценка псевдообратной матрицы несколько упрощается и сводится к следующему. Выберем n моментов этапов времени ti, представив соотношение (15) для этих моментов в виде [5]
Используя метод наименьших квадратов, найдем оценку матрицы B по формуле $\hat {B} = {{[y]}^{{\text{T}}}}{{[{{[{{u}_{j}}\left( {{{t}_{i}}} \right) - u_{j}^{0}]}^{{\text{T}}}}]}^{ + }}$. Далее с помощью стандартных функций MATLAB определим оценку псевдообратной матрицы [3] ${{\hat {B}}^{ + }}$ = ${{[{{[y]}^{{\text{T}}}}]}^{ + }}{{[{{u}_{j}}\left( {{{t}_{i}}} \right) - u_{j}^{0}]}^{{\text{T}}}}$. В этом случае для получения оценки матрицы B используют опытные данные uj(t) и $u_{j}^{0},$ полученные по предыстории. В соответствии с желаемым законом управления, пропорциональным интегралу от изменения выходной характеристики, значения yj(ti) приближенно рассчитывают по формуле
Каждую строку uj(ti) получают из соответствующего столбца, т.е. транспонированием матрицы исходных данных. Для нахождения оценки псевдообратной матрицы аналогично определяют транспонированную матрицу ${{[{{u}_{j}}\left( {{{t}_{i}}} \right) - u_{j}^{0}]}^{{\text{T}}}}$. При этом строку получают из соответствующего столбца, в котором каждый элемент можно определить как разность между следующим и первым элементами данного столбца. Полученную оценку псевдообратной матрицы в дальнейшем используют как постоянную матрицу для определения параметров управлений, подставив ее в (17).
Методика нахождения управляющих воздействий на этапе создания сложных систем сводится к следующему: 1) составляют матрицу u = [uij] исходных данных – конструктивных, технологических и эксплуатационных параметров uij, наработок на отказ или интенсивностей отказов, или вероятностей безотказной работы за заданное время t для соответствующего i-го этапа жизни изделия; 2) по исходной матрице u = [uij] в соответствии с выбранным законом управления и заданной желаемой динамикой развития выходной характеристики определяют транспонированные матрицы параметров управлений и выходной характеристики [uT], [yT]; 3) с использованием стандартных функций MATLAB [3] определяют транспонированную псевдообратную матрицу [y+]T; 4) рассчитывают оценку псевдообратной матрицы ${{\hat {B}}^{ + }}$ = $[{{u}^{{\text{T}}}}]{{[{{y}^{ + }}]}^{{\text{T}}}}$, которую в последующем применяют как постоянную; 5) заключительный этап – определение управляющего воздействия по формуле, полученной в соответствии с выбранным желаемым законом управления и заданной динамикой развития выходной характеристики.
Методика нахождения управляющих воздействий апробирована при создании подвижных установок для ракетных комплексов (1976, 1982, 1987 гг.).
Пример. В процессе испытаний подвижной установки специального назначения были зафиксированы отказы конструктивного и технологического характера отдельных узлов и исполнительных механизмов, которые снижали надежность подвижной установки в целом. Результаты проведенных доработок в виде изменения соответствующих параметров (исходные данные) сведены в табл. 2 (пример заимствован из [2]).
Таблица 2
| u1, ° | u2, МПа | u3, шт | u4, см | u5, МПа | y1 · 10–4, ч | y2 · 10–4, ч | y3 · 10–4, ч | y4 · 10–4, ч | y5 · 10–4, ч | t · 10–4, ч |
|---|---|---|---|---|---|---|---|---|---|---|
| 1.50 | 18 | 10.0 | 15.0 | 0.3 | 1.00 | 6.00 | 3.00 | 2.00 | 1.50 | 0.14 |
| 1.30 | 20 | 8.0 | 16.0 | 0.6 | 1.20 | 8.00 | 5.00 | 6.20 | 2.50 | 0.36 |
| 1.20 | 25 | 6.5 | 16.8 | 0.8 | 1.50 | 9.50 | 5.80 | 9.70 | 3.30 | 0.58 |
| 1.08 | 30 | 5.0 | 17.5 | 1.0 | 1.80 | 10.70 | 6.50 | 12.90 | 4.00 | 0.86 |
| 1.00 | 37 | 4.0 | 18.1 | 1.0 | 2.00 | 11.80 | 7.20 | 15.90 | 4.60 | 1.08 |
| 0.91 | 45 | 3.0 | 18.6 | 1.2 | 2.50 | 12.80 | 7.80 | 18.70 | 5.10 | 1.22 |
| 0.85 | 50 | 2.2 | 19.0 | 1.3 | 3.00 | 13.60 | 8.40 | 20.70 | 5.50 | 1.44 |
| 0.80 | 55 | 1.5 | 19.3 | 1.3 | 3.80 | 14.10 | 8.90 | 21.80 | 5.80 | 1.48 |
| 0.75 | 70 | 1.0 | 19.5 | 1.4 | 4.50 | 14.50 | 10.30 | 22.80 | 6.10 | 1.51 |
| 0.70 | 90 | 0.7 | 19.6 | 1.5 | 6.00 | 15.00 | 10.50 | 23.60 | 6.30 | 1.55 |
Требуется определить оптимальные параметры управления в виде изменения геометрических параметров конструкции, технологических процессов и т.п., подтверждающие требуемую наработку на отказ yтр за T0 = 5 лет ≈ 50 000 ч. В условных единицах yтр рассчитывается как отношение количества часов в году к требуемой наработке на отказ T0, т.е. yтр = y(t) = 8640/50 000 = 0.1728.
Решение 1. Задаем желаемую динамику развития выходной характеристики в форме экспоненциальной зависимости для закона Вейбулла α = 1
2. Выберем желаемый закон управления, пропорциональный интегралу от изменения выходной характеристики
3. Результаты статистических данных, полученных при отработке изделия-аналога, сведены в табл. 2.
4. В соответствии с выбранным желаемым законом управления преобразуем таблицу исходных данных к исходным матрицам, при этом
В результате преобразования получим матрицы u и y(t) размерностью m × (n – 1)
5. Транспонируем исходную матрицу u
6. Для исходной матрицы y(t) транспонированную псевдообратную матрицу [y+]T найдем с помощью стандартных функций MATLAB [3, 5]
7. Используя метод наименьших квадратов, найдем оценку псевдообратной матрицы ${{\hat {B}}^{ + }}$ = uT[y+]T [3, 5]
8. Для заданной желаемой динамики развития выходной характеристики и выбранного желаемого закона управления управляющие воздействия определим по выражению ${{u}_{j}}\left( t \right)$ = $u_{j}^{0}$ + $T(1 - {\text{exp}}( - t{\text{/}}T)){{\hat {B}}^{ + }}{{y}^{{{\text{т р }}}}}$, которое преобразуем, приняв период отработки T0= 3 года и T = T0/3;
Подставив в формулу (11) исходные данные $u_{j}^{0}$, ${{\hat {B}}^{ + }},$ yтр и t = 0, 1, 2, 3, получим расчетные значения параметров управления (табл. 3).
Таблица 3
| Параметр управления | Период отработки, год | |||
|---|---|---|---|---|
| 0 | 1 | 2 | 3 | |
| u1(t) – угол, при котором одновременно срабатывают блокировки | 1.50 | 1.28 | 1.20 | 1.17 |
| u2(t) – измененная прочность материала металлоконструкций, МПа | 18.00 | 83.40 | 107.46 | 116.32 |
| u3(t) – число сварных швов определенной длины на металлоконструкциях | 10.00 | 9.44 | 9.23 | 9.16 |
| u4(t) – изменение диаметра штока домкрата, см | 15.00 | 15.15 | 15.20 | 15.22 |
| u5(t) – изменение давления в бустере муфты силового привода, МПа | 0.30 | 0.20 | 0.16 | 0.15 |
Анализ полученных значений параметров управления показывает, что параметры u1(t), u2(t), u3(t), u4(t) и u5(t) отражают положительную динамику изменения выходной характеристики и соответствуют физическому смыслу дорабатываемого узла.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 17-01-00018.
Список литературы
Гартунг Ю.А. Исследование развития динамических систем, обусловленного некоторыми дифференциальными программами. М.: Наука, 1984. 59 с.
Труханов В.М. Надежность в технике. М.: ООО Издательский дом “Спектр”, 2017. 656 с.
Труханов В.М. Метод достижения и обеспечения заданного уровня надежности изделий машиностроения на основе управляющих воздействий // Проблемы машиностроения и надежности машин. 2005. № 3. С. 96–100.
Труханов В.М. Математическая модель изменения уровня надежности изделий с учетом управляющих воздействий, выраженных в виде вероятностей // Проблемы машиностроения и надежности машин. 2014. № 2. С. 44–47.
Труханов В.М. Математические модели роста уровня надежности технической системы с учетом управляющих воздействий, выраженных в виде вероятностей и наложенных ограничений // Проблемы машиностроения и надежности машин. 2016. № 4. С. 39–43.
Дьяконов В.П. MATLAB. Полный самоучитель. М.: ДМК-Пресс, 2017. 768 с.
Гантмахер Ф.Р. Теория матриц. М.: ФИЗМАТЛИТ, 2004. 560 с.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин