Проблемы машиностроения и надежности машин, 2019, № 2, стр. 68-77

В разрабатываемых узлах трения (подшипниковые опоры, зубчатые и фрикционные и др. передачи) для различных машиностроительных отраслей используется контакт шероховатых металлических поверхностей, которые работают при различных смазках, в том числе и смазке водой. Исследования указывают на существенную зависимость несущей способности смазочного слоя и долговечности узлов трения от параметров шероховатости металлических поверхностей. Практика свидетельствует о существенной трансформации исходной шероховатости до оптимальных значений ее параметров, определяющих контактные давления и толщины смазочных слоев эксплуатируемых узлов трения.

Исследованию влияния шероховатости на характеристики смазочного слоя в смазываемых узлах трения посвящено большое количество работ. В работах [1–3] рассмотрены смазываемые контакты жестких шероховатых поверхностей, исследовано влияние поперечных и продольных шероховатостей на характеристики смазочного слоя. Деформации тел при этом не учитывали. В работах [4, 5] учитывалось влияние деформаций на характеристики смазываемого контакта шероховатых тел. Было отмечено, что деформации тел сглаживают неровности. В результате высота микронеровностей в области высокого давления меньше исходной высоты микронеровностей. Однако во всех приведенных работах не рассматривались предельные нагрузки, когда небольшое увеличение нагрузки приводит к переходу из упруго-гидродинамического режима в смешанный режим.

В настоящей статье приведено исследование контактного взаимодействия двух металлических цилиндрических контртел при их внешнем контакте и смазке маловязким маслом. Параметры шероховатостей варьируются в широком диапазоне. Определены условия, при которых происходит переход из упругогидродинамического режима в режим смешанного трения. По результатам этих исследований устанавливаются оптимальные параметры шероховатости металлического контртела.

Математическая модель. Математическая модель смазываемого контакта двух упругих шероховатых цилиндров в режиме упруго-гидродинамического трения включает в себя уравнения, определяющие толщину смазочного слоя, распределение давления в смазочном слое, реологические свойства смазки, необходимые начальные и граничные условия.

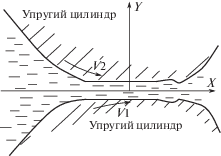
Схема контакта приведена на рис. 1. Начнем с уравнений, определяющих толщину смазочного слоя. Рассмотрим смазочный слой между поверхностями двух упругих шероховатых цилиндров. Направим ось $X$ системы координат $OXY$ в сторону движения смазочного слоя, начало системы координат поместим на линии действия нагрузки $Q$. Полагая, что область, в которой развивается высокое давление, мала по сравнению с радиусами цилиндров, уравнение поверхности i-го цилиндра (i = 1, 2) запишем в виде

где $i = 1$ относится к нижнему цилиндру, а $i = 2$ – к верхнему цилиндру, ${{W}_{i}}$ – перемещение поверхности i-го цилиндра вследствие его деформаций, значение ${{W}_{i}}$ считается положительным, если оно направлено по нормали внутрь цилиндра, ${{\tilde {\varepsilon }}_{i}}(X,t)$ – функция, которая задает шероховатость движущейся поверхности i-го цилиндра, ${{\Delta }_{i}}$ – $Y$‑координата недеформированной средней поверхности i-го цилиндра при $X = 0$.

Если поверхность i-го цилиндра в области контакта движется по направлению оси $X$ со скоростью ${{V}_{i}}$, то функцию ${{\tilde {\varepsilon }}_{i}}(X,t)$ можно представить в виде

где ${{\tilde {X}}_{i}}$ – координата, привязанная к поверхности $i$-го цилиндра, ${{\tilde {\varepsilon }}_{i}}({{\tilde {X}}_{i}})$ – функция, задающая шероховатость поверхности в системе координат, в которой поверхность неподвижна.

Функцию ${{\tilde {\varepsilon }}_{i}}({{\tilde {X}}_{i}})$ принимаем в виде

где ${{R}_{{q,}}}_{i}$ – высота микронеровностей $i$-й поверхности; ${{{\lambda }}_{i}}$ – шаг микронеровностей $i$-й поверхности; ${{\beta }_{i}}$ – фаза неровностей $i$-й поверхности.

При отсутствии шероховатости угловое положение цилиндра не играет роли. Однако при наличии шероховатости угловое положение цилиндра определяет характер поведения толщины смазочного слоя в месте его обрыва. Это приводит к зависимости решения задачи от углового положения цилиндра.

Толщина смазочного слоя равна

где $\varepsilon (X,t)$ = $2{{R}_{{q,1}}}\sin \left( {2{\pi }\frac{{X - {{V}_{1}}t}}{{{{{\lambda }}_{1}}}} + {{\beta }_{1}}} \right)$ + $2{{R}_{{q,2}}}\sin \left( {2{\pi }\frac{{X - {{V}_{2}}t}}{{{{{\lambda }}_{2}}}} + {{\beta }_{2}}} \right)$; $R$ – приведенный радиус.

Пусть $C$ есть значение координаты $X$, в которой происходит разрушение смазочного слоя. Принимая в уравнении (1) значение $X$ равным $C$ и вычитая полученное уравнение из уравнения (1), найдем

где ${{\tilde {h}}_{c}}$ – толщина смазочного слоя в месте его обрыва.

Перемещение поверхности цилиндра ${{W}_{i}}$ функционально связано с распределением давления $P(X,t)$, развиваемым в смазочном слое. Временная зависимость давления $P$ обусловлена не стационарностью процессов в смазочном слое при временной зависимости скоростей ${{V}_{1}}$ и ${{V}_{2}}$, а также изменением толщины смазочного слоя со временем вследствие движения шероховатостей поверхностей. Таким образом, даже при постоянных значениях скоростей ${{V}_{1}}$ и ${{V}_{2}}$ давление в смазочном слое будет изменяться со временем.

Если цилиндры проявляют упругие свойства, то перемещения поверхности связаны с приложенным к ней давлением соотношением [1]

где ${{\nu }_{i}}$ – коэффициент Пуассона $i$-го цилиндра, ${{E}_{i}}$ – его модуль упругости.

Из (3) следует

Из (2) и (4) следует выражение для толщины смазочного слоя при известной функции распределения давления $P(X,t)$

где $E{\text{'}}$ – приведенный модуль упругости, определяемый по формуле

Распределение давления в смазочном слое в гидродинамическом режиме определяем из нестационарного уравнения Рейнольдса [7]

где $V = ({{V}_{1}} + {{V}_{2}}){\text{/2}}$.

Для учета изменения вязкости жидкости с изменением давления используем модель Баруса [7]

где ${{\mu }_{0}}$ – вязкость смазки при атмосферном давлении, $\alpha $ – пьезокоэффициент вязкости.

Зависимость плотности смазочного материала от давления примем в виде, предложенном в [7]

где ${{\rho }_{0}}$ – плотность смазки при атмосферном давлении, ${{C}_{1}}$, ${{C}_{2}}$ – константы.

Для уравнения Рейнольдса должны быть заданы граничные условия. Принимаем обычные для теории смазки условия

Здесь $A$ – левая (входная) граничная точка смазочного слоя. В режиме обильной смазки при аналитическом анализе обычно принимают $A = - \infty $. Однако при численном решении должно быть задано конкретное число. Его надо задавать достаточно большим, чтобы замена бесконечности на конечное число не привела к большой погрешности.

Давление, развиваемое в смазочном слое, уравновешивает приложенную к цилиндрам нагрузку, т.е.

где $Q$ – нагрузка на единицу длины цилиндров, которая в общем случае может зависеть от времени.

Кроме условий (5), (6) должны быть заданы начальные условия, которые в каждой конкретной задаче должны быть сформулированы.

После решения указанной системы уравнений можно определить составляющую касательных сил, действующих со стороны смазочного слоя на цилиндр

и момент сил, действующих со стороны смазочного слоя на цилиндр

После определения силы ${{F}_{t}}$ и момента $M$ коэффициент трения можно определить по формуле

При численном решении системы уравнений она приводится к безразмерному виду. Рассмотрим случай контакта упругих шероховатых цилиндров, разделенных тонким слоем смазочного материала. Полагаем, что нагрузка не зависит от времени, а скорость может меняться со временем. Введем безразмерные переменные по формулам

где b – половина ширины площадки контакта, которая была бы при сухом контакте упругих цилиндров с приведенным радиусом R.

В безразмерных переменных задача формулируется следующим образом

где ${{K}_{1}} = {{P}_{g}}{{C}_{1}}$, ${{K}_{2}} = {{P}_{g}}{{C}_{2}}$, $G = \alpha {{P}_{g}}$, ${{\bar {R}}_{{q,1}}}$ = $\frac{{4R{{R}_{{q,1}}}}}{{{{b}^{2}}}}$, ${{\bar {R}}_{{q,2}}}$ = $\frac{{4R{{R}_{{q,2}}}}}{{{{b}^{2}}}}$, $S = 3{{\pi }^{2}}\frac{{{{\mu }_{0}}VRE{\text{'}}}}{{{{Q}^{2}}}}$, ${{k}_{1}} = \frac{b}{{{{\lambda }_{1}}}}$, ${{k}_{2}} = \frac{b}{{{{\lambda }_{2}}}}$, ${{u}_{1}} = \frac{{{{V}_{1}}}}{V}$ = $\frac{{2{{V}_{1}}}}{{{{V}_{1}} + {{V}_{2}}}}$, ${{u}_{2}} = \frac{{{{V}_{2}}}}{V}$ = $\frac{{2{{V}_{2}}}}{{{{V}_{1}} + {{V}_{2}}}}$.

После решения приведенной системы уравнений коэффициент трения может быть определен по формуле

Если скорость качения меняется со временем, то параметр $S$ зависит от безразмерного времени $\bar {t}$. Если скорость качения постоянна, но шероховатость учитывается, то процесс будет нестационарным, т.е. толщина смазочного слоя и давление в нем будут зависеть от времени. Только в случае постоянства скорости и не учете шероховатости задача становится стационарной.

Метод численного решения. Для численного решения приведенной системы уравнений они заменяются системой нелинейных алгебраических уравнений, которая решается методом Ньютона. Система алгебраических уравнений получается после замены интегралов конечными суммами, а производных – конечными разностями.

Предположим, что известны значения функций $c(\bar {t})$, $h(x,\bar {t})$, $p(x,\bar {t})$ в момент времени $\bar {t} = {{\bar {t}}^{{I - 1}}}$, т.е. известны значения величин ${{c}^{{I - 1}}}$ = $c({{\bar {t}}^{{I - 1}}})$ и функций ${{h}^{{I - 1}}}(x)$ = = $h(x,{{\bar {t}}^{{I - 1}}})$, ${{p}^{{I - 1}}}(x)$ = $p(x,{{\bar {t}}^{{I - 1}}})$. Покажем, как вычисляются в настоящей статье значения этих функций в момент времени ${{\bar {t}}^{I}}$ = ${{\bar {t}}^{{I - 1}}} + \Delta t$, где $\Delta t > 0$ – заданная величина. То есть, как вычисляются значения величин ${{c}^{I}}$ = $c({{\bar {t}}^{I}})$ и функций ${{h}^{I}}(x)$ = $h(x,{{\bar {t}}^{I}})$, ${{p}^{I}}(x)$ = $p(x,{{\bar {t}}^{I}})$. Так как значения функций в момент времени $t = 0$ известны, то, задавая шаг по времени, и повторяя процедуру можно определить значения этих функций в любой момент времени.

В качестве начального приближения этой величины ${{c}^{I}}$ = $c({{\bar {t}}^{I}})$ принимаются ее значения в момент времени $\bar {t} = {{\bar {t}}_{{I - 1}}}$. При выполнении каждой итерации эти значения известны, что позволяет ввести в отрезке $[a,{{c}^{I}}]$ неравномерную сетку. Обозначим

присвоим переменной $t$ значение ${{t}^{I}}$ и проинтегрируем обе части этого уравнения на отрезке $[0.5({{x}^{{j - 1}}} + {{x}^{j}})$, $0.5({{x}^{j}} + {{x}^{{j + 1}}})]$. При интегрировании функции $s\left( x \right)$ представим ее сплайн функцией первого порядка где ${{\text{v}}_{r}}\left( x \right)$ – кусочно-линейная функция на отрезке $[a,x_{k}^{I}]$, ${{\text{v}}_{r}}(x) = 1$, если $x = {{x}_{r}}$, ${{\text{v}}_{r}}(x) = 0$, если $x = {{x}_{i}}$, $i \ne r$.

Заменим полученные после интегрирования производные первого порядка конечными разностями. При этом внесем экспоненту, входящую в выражение для вязкости смазочного материала под знак дифференциала. В результате получим следующие уравнения

Принимая в уравнении (11) последовательно $x = {{x}_{{I,i}}}$, $i = 0,1,\; \ldots ,\;{{N}_{I}} - 1$, интегрируя в промежутке $\left( {{{{\bar {t}}}_{{I - 1}}},{{{\bar {t}}}_{I}}} \right)$ и воспользовавшись при вычислении интеграла формулой трапеций, получаем

Принимая в (8) $\bar {t} = {{\bar {t}}_{I}}$, $x = {{x}_{i}}$, $i = 0,1,\; \ldots ,\;{{N}_{I}} - 1$ и подставляя вместо функции ${{p}_{I}}(x)$ сплайн-функцию первого порядка, после интегрирования получаем

Производные в граничных условиях заменяем конечными разностями. Интеграл в (10) заменим конечной суммой. В результате получаем соотношение

Граничные условия принимают вид

Уравнения (12)–(15) представляют собой систему $3{{N}_{I}} + 5$ уравнений относительно $3{{N}_{I}} + 5$ неизвестных ${{h}_{{I,i}}}$, ${{p}_{{I,i}}}$, ${{s}_{{I,i}}}$, ${{h}_{{0,I}}}$ и ${{c}_{I}}$. Запишем эту систему уравнений в виде

где $({{X}_{1}},{{X}_{2}},\; \ldots ,\;{{X}_{{3{{N}_{I}} + 5}}}) = ({{h}_{{I,i}}},{{p}_{{I,i}}},{{s}_{{I,i}}},{{h}_{{0,I}}}{{c}_{I}})$, $i = 0,1,\; \ldots ,\;{{N}_{I}}$.

Система уравнений (16) решается итерациями с использованием метода Ньютона. Итерации по методу Ньютона завершаются при выполнении условия

где $\varepsilon $ – заданная величина. В расчетах принималось $\varepsilon = {{10}^{{ - 6}}}$.

При расчетах число узлов сетки выбиралось таким образом, чтобы на половине длины шероховатости располагалось не менее 15 узлов сетки. Максимальное число узлов сетки оказалось равным 120. Время счета одного варианта составляет порядка 2 минут.

Анализ результатов расчета. Были проведены расчеты двух смазанных металлических цилиндров диаметром 100 мм и с осевым размером b = 5 мм. Расчеты проводились для двух вариантов: сталь – сталь при E ' = 205 ГПа; сталь – бронза при E ' = 110 ГПа; высота неровностей R_q менялась от 0.2 до 1.2 мкм. Шаг неровностей изменялся от 250 мкм до 500 мкм. Скорость качения принималась равной 5.2 м/сек с эффективным удельным скольжением равным 0.02. Нормальная нагрузка, отнесенная к единице длины цилиндров, принималась равной 400 и 800 кН. Вязкость смазки принята 0.03 Па · сек.

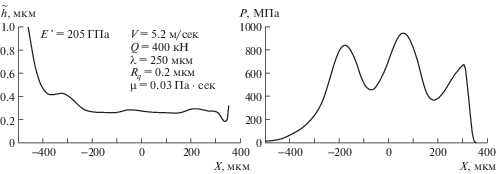
Анализ расчетов показывает, что деформации тел существенно уменьшают высоту неровностей в области высокого давления. При этом давление имеет максимум в области, в которой выступ шероховатости уменьшает толщину смазочного слоя, и минимум, где шероховатость способствует увеличению толщины смазочного слоя. Такое распределение давления приводит к тому, что при значениях параметров, приведенных на рис. 2, и при исходной шероховатости R_q = 0.2 мкм, колебания толщины смазочного слоя в области высокого давления не превышают 0.03 мкм, т.е. почти в 7 раз меньше. В результате этого изменение толщины смазочного слоя в области высокого давления, обусловленное шероховатостью, мало по сравнению со средним значением толщины в этой области.

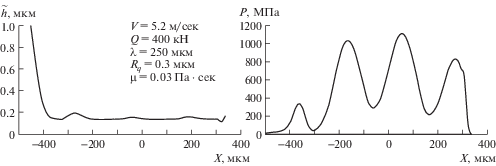
Хотя пульсации толщины смазочного слоя в области высокого давления гасятся деформациями тел, пульсации распределения давления в этой области велики и они растут с ростом высоты микронеровностей. Когда высота микронеровностей достигает определенного значения, происходит разрыв смазочного слоя и контакт переходит в режим смешанного трения. Это хорошо иллюстрируют результаты расчетов, приведенные на рис. 2 и 3, где приведены зависимости $\tilde {h}$ и P(X) при Q = 400 кН, V = 5.2 м/с, μ = 0.03 Па · с, λ = 250 мкм, R_q = 0.2 мкм (рис. 2) и R_q = 0.3 мкм (рис. 3). Видно, что при R_q = 0.2 мкм локальные минимумы давления имеют порядок 400 МПа, а при R_q = = 0.3 мкм один из локальных минимумов имеет порядок нескольких МПа. Это означает, что при более высокой высоте микронеровностей контакт переходит в режим смешанного трения.

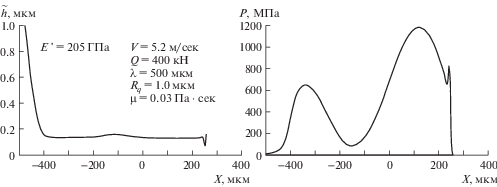
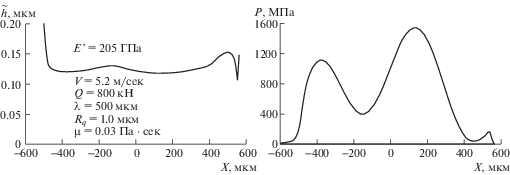
Значение высоты микронеровностей R_q, при которой происходит переход из гидродинамического режима в режим смешанного трения, существенно зависит от шага микронеровностей (рис. 3 и 4). На рис. 4 результаты получены при шаге микронеровностей λ = 500 мкм и при тех же значениях остальных параметров, что и на рис. 3. Видно, что при шаге λ = 500 мкм переход в режим смешанного трения происходит при высоте микронеровностей выше 1 мкм, в то время как при шаге микронеровностей λ = 250 мкм переход в режим смешанного трения происходит при высоте микронеровностей порядка 0.3 мкм.

Рост нагрузки приводит к уменьшению толщины смазочного слоя, но слабо влияет на высоту микронеровностей, при которой происходит переход в режим смешанного трения. Об этом свидетельствует сопоставление данных (рис. 4) с данными (рис. 5), на котором приведены результаты расчетов при Q = 800 кН.

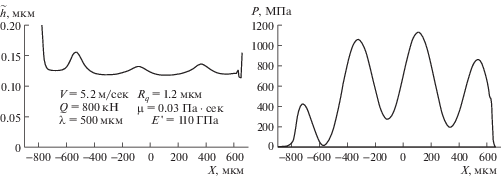
Уменьшение модуля упругости контактирующих тел приводит к увеличению размера области высокого давления, высоты микронеровностей, при которой происходит переход в режим смешанного трения. В этом можно убедиться, сопоставляя результаты расчетов, приведенных на рис. 5 и 6. На рис. 6 приведены результаты расчетов для пары трения сталь – бронза с приведенным модулем упругости E ' = 110 ГПа. Видно, что пара сталь – бронза переходит в режим смешанного трения при R_q = 1.2 мкм, в то время как пара трения сталь – сталь переходит в режим смешанного трения при R_q = = 1.0 мкм.

Таким образом, предложенная математическая модель для исследования влияния шероховатости в смазываемом контакте упругих шероховатых поверхностей позволяет исследовать характеристики смазочного слоя, по которым определяются условия перехода из упругогидродинамического режима в режим смешанного трения.

Работа выполнена в рамках ФЦП “Исследования и разработки по приоритетным направлениям развития научно-технического комплекса России на 2014–2020 гг.”. Проект RFMEFI57815X0108.