Проблемы машиностроения и надежности машин, 2019, № 2, стр. 27-39
ИДЕНТИФИКАЦИЯ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК УПРУГОСТИ И ДЕМПФИРУЮЩИХ СВОЙСТВ ТИТАНОВОГО СПЛАВА ОТ-4 НА ОСНОВЕ ИССЛЕДОВАНИЯ ЗАТУХАЮЩИХ ИЗГИБНЫХ КОЛЕБАНИЙ ТЕСТ-ОБРАЗЦОВ
В. Н. Паймушин 1, 2, *, В. А. Фирсов 1, В. М. Шишкин 3
1 Казанский национальный исследовательский технический университет им. А.Н. Туполева
г. Казань, Россия
2 Казанский федеральный университет
г. Казань, Россия
3 Вятский государственный университет
г. Киров, Россия
* E-mail: vpajmushin@mail.ru
Поступила в редакцию 18.08.2017
Принята к публикации 24.12.2018
Аннотация
В статье показано значительное снижение динамического модуля упругости титанового сплава ОТ-4 в диапазоне частот 0–25 Гц по сравнению со статическим модулем упругости с дальнейшей стабилизацией отмеченного динамического модуля при частотах 25–80 Гц на основе исследования затухающих изгибных колебаний серии консольно закрепленных тест-образцов; разработана методика идентификации демпфирующих свойств отмеченного сплава при растяжении – сжатии с учетом внутреннего и внешнего аэродинамического демпфирования на основе метода конечных элементов и минимизации целевой функции, содержащей экспериментальные и расчетные логарифмические декременты колебаний тест-образца; построена матрица аэродинамического демпфирования конечного элемента на основе аппроксимации Морисона для представления погонной силы аэродинамического сопротивления при колебаниях тест-образца; получена усредненная по нескольким тест-образцам амплитудная зависимость логарифмического декремента колебаний, представляющая демпфирующие свойства исследуемого сплава ОТ-4.
Введение. Титановые сплавы отличаются высокой удельной прочностью и жесткостью в сочетании с высокой термической и коррозионной стойкостью, что открывают большие перспективы их применения в авиационной промышленности, ракетостроении и транспортном машиностроении. Это определяет необходимость адекватного определения их упругих и демпфирующих свойств, соответствующих реальным условиям режимов работы конструкции.
В расчетах по определению динамической реакции конструкций в колебательных режимах деформирования традиционно используются характеристики упругости материала, найденные при статических испытаниях соответствующих тест-образцов. Однако проведенные динамические испытания дюралюминиевых тест-образцов в режимах изгибных затухающих и резонансных колебаний в диапазоне частот 0–200 Гц [1] показали значительное снижение экспериментально измеренных частот по сравнению с их расчетными значениями, найденными с использованием статического модуля упругости дюралюминия, что нельзя объяснить погрешностями эксперимента, а только существенным снижением модуля упругости дюралюминия в указанном диапазоне частот по сравнению с его статическим номиналом. Это означает, что использование в динамических режимах деформирования статического модуля упругости материала может дать значительные ошибки в определении резонансных частот и динамической напряженности элементов конструкций. Отсюда вытекает необходимость определения упругих свойств других перспективных конструкционных материалов в динамических режимах деформирования.
К числу наименее исследованных механических характеристик титана и его сплавов относится демпфирующая способность, влияющая на динамическую напряженность элементов конструкции в циклических режимах деформирования и, прежде всего, при резонансе, реализующихся в конструкции при совпадении частот ее собственных колебаний с частотой внешнего циклического воздействия. При таком режиме нагружения многократно возрастают амплитудные значения параметров динамического напряженно-деформированного состояния (НДС). Корректное и достоверное их теоретическое определение с необходимой для практических целей точностью требует надлежащего учета в расчетных соотношениях демпфирующих свойств материалов конструкций, обусловленных внутренним трением.
Для экспериментального исследования демпфирующих свойств материалов в диапазоне частот от 50 до 5000 Гц в настоящее время существует международный стандарт ASTM E-756 [2], в соответствии с которым акустическим методом в резонансном режиме исследуются изгибные колебания консольно закрепленных тест-образцов различной структуры. Однако указанный стандарт имеет целый ряд ограничений, сужающих область его применения: 1) невозможно исследование демпфирующих свойств материалов в диапазоне частот от 0 до 50 Гц, наиболее полно отражающим реальные условия эксплуатации большинства конструкций; 2) демпфирующие свойства материалов исследуются в условиях малых амплитуд перемещений, что ограничивает использование полученных результатов для оценки динамического поведения конструкций с большими эксплуатационными амплитудами колебаний, например, лопастей несущих и управляющих винтов вертолетов, ветроэнергоустановок и т.д.; 3) не учитывается демпфирование воздушной среды при колебаниях тест-образцов, что, как показали проведенные исследования [3], может привести к существенным погрешностям в определении демпфирующих свойств как материала так и конструкции в целом, поскольку составляющая внешнего аэродинамического демпфирования будет приписываться к определяемой демпфирующей способности материала.
Имеющиеся экспериментальные и теоретические методы учета аэродинамического демпфирования при изгибных колебаниях тест-образцов в основном направлены на получение коэффициентов аэродинамического сопротивления и структурных формул для вычисления аэродинамической составляющей демпфирования [4–6], что не вписывается в общую конечно-элементную идеологию моделирования динамической реакции по причине отсутствия обоснованных методов получения матрицы аэродинамического демпфирования тест-образца. Наиболее приемлемый способ получения данной матрицы может состоять в использовании классической аппроксимации Морисона [7, 8] для представления погонных сил аэродинамического сопротивления протяженных объектов и конструкций, но данный вопрос пока остается открытым.
Необходимо отметить, что характеристики демпфирования материалов, получаемые при изгибных колебаниях тест-образцов, являются лишь сравнительной оценкой их демпфирующих свойств, и не могут быть использованы в условиях отличных от эксперимента [9]. Отсюда возникает необходимость идентификации реальных демпфирующих свойств материала по экспериментальным характеристикам демпфирования тест-образцов в условиях изгибных колебаний. Данные характеристики получают путем исследования резонансных или затухающих изгибных колебаний тест-образцов. Но проведение эксперимента в условиях резонанса требует чрезвычайно точной настройки частоты источника колебаний из-за высокой чувствительности амплитуды колебаний тест-образца к малым изменениям частоты вблизи резонанса. Поэтому идентификацию демпфирующих свойств материалов более удобно и надежно проводить на основе исследования затухающих изгибных колебаний, соответствующих тест-образцов [3, 10].
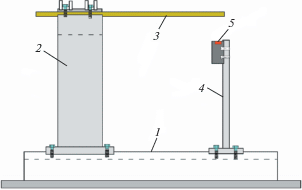
Экспериментальная установка для исследования затухающих изгибных колебаний тест-образцов. На кафедре прочности конструкций Казанского национального исследовательского технического университета им. А.Н. Туполева разработана специальная экспериментальная установка [3] для определения динамических характеристик упругости и демпфирующих свойств материалов (изотропных, композитных, эластичных) на основе исследования затухающих изгибных колебаний соответствующих тест-образцов (рис. 1). Установка состоит из основания 1 и силовой стенки 2, жестко соединенных между собой. На стенке консольно закрепляется испытуемый тест-образец 3. Защемление осуществляется с помощью разнесенных планок, соединяемых со стенкой двумя рядами болтовых соединений и исключающих поворот испытуемого тест-образца в сечении заделки. На основании установлена стойка 4 для крепления лазерного датчика перемещений 5, положение которой вдоль основания может изменяться для измерения амплитуды колебаний точек тест-образца при изменении его стрелы вылета.
В установке используется триангуляционный лазерный датчик фирмы RIFTEK (RF603-X/100), обеспечивающий точность измерения амплитуды колебаний 0,01 мм. Результаты измерений в цифровом формате поступают на персональный компьютер. Замеры начинаются с некоторой задержкой по времени, необходимой для перехода из начального (статического) изогнутого состояния на низшую форму колебаний тест-образца. Разработанное математическое обеспечение позволяет осуществить до 2000 замеров прогиба в секунду, и, таким образом, весьма точно отразить реальную виброграмму затухающих колебаний испытуемого образца.
Идентификация частной зависимости динамического модуля упругости титанового сплава ОТ-4. Проведены динамические испытания в режиме затухающих изгибных колебаний серии консольно закрепленных тест-образцов прямоугольного поперечного сечения с длинами L = 140–750 мм, что соответствует диапазону экспериментально измеренных частот ${{f}_{*}}$ = 73.3–2.68 Гц. Статический модуль упругости и плотность сплава ОТ-4: E = 1.1 × 105 МПа; ρ = 4430 кг/м3. Ширина и толщина тест-образцов: b = 20 мм; h = 1.94 мм. Значения динамического модуля упругости отмеченного сплава в указанном диапазоне частот ${{f}_{*}}$ определялись по формуле
следующей из известного соотношения для нахождения низшей частоты свободных изгибных колебаний консольно закрепленного стержня(2)
$f = {{(1.875{\text{/}}L)}^{2}}\sqrt {EI{\text{/}}m} {\text{/(2}}\pi {\text{)}};\quad I = b{{h}^{3}}{\text{/}}12;\quad m = \rho bh.$В табл. 1 приведены длины L тест-образцов, их экспериментальные частоты ${{f}_{*}}$, соответствующие расчетные частоты f, полученные по формуле (2) при статическом модуле упругости E = 1.1 × 105 МПа (для сравнения их с частотами ${{f}_{*}}$), относительное расхождение частот $\Omega = ({{f}_{{\text{*}}}} - f){\text{/}}f$ и значения динамического модуля упругости Ed сплава ОТ-4, полученные по формуле (1) при частотах ${{f}_{*}}$. Обращает на себя внимание факт систематического и значительного снижения экспериментальных частот ${{f}_{*}}$ тест-образцов по сравнению с соответствующими расчетными частотами f, полученными при статическом модуле упругости E = 1.1 × 105 МПа, что нельзя истолковать погрешностями эксперимента (в этом случае величины Ω имели бы больший разброс и различные знаки). Данный факт можно объяснить только существенно меньшим значением динамического модуля упругости Ed исследуемого сплава по сравнению с его статическим модулем упругости E.
Таблица 1.
| L, мм | ${{f}_{{\text{*}}}}$, Гц | f, Гц | Ω | Ed, МПа |
|---|---|---|---|---|
| 140 | 73.30 | 79.67 | –0.0800 | 0.9310 × 105 |
| 150 | 64.09 | 69.41 | –0.0766 | 0.9380 × 105 |
| 160 | 56.00 | 61.00 | –0.0820 | 0.9270 × 105 |
| 175 | 47.87 | 50.99 | –0.0612 | 0.9694 × 105 |
| 200 | 36.20 | 39.04 | –0.0727 | 0.9458 × 105 |
| 225 | 28.94 | 30.85 | –0.0619 | 0.9682 × 105 |
| 250 | 23.31 | 24.99 | –0.0672 | 0.9574 × 105 |
| 275 | 19.49 | 20.65 | –0.0562 | 0.9799 × 105 |
| 300 | 16.35 | 17.35 | –0.0576 | 0.9767 × 105 |
| 325 | 13.86 | 14.78 | –0.0622 | 0.9667 × 105 |
| 400 | 9.30 | 9.76 | –0.0471 | 0.9987 × 105 |
| 500 | 6.04 | 6.25 | –0.0336 | 1.0285 × 105 |
| 600 | 4.23 | 4.34 | 0.0253 | 1.0460 × 105 |
| 700 | 3.08 | 3.20 | –0.0375 | 1.0274 × 105 |
| 750 | 2.68 | 2.78 | –0.0360 | 1.0251 × 105 |
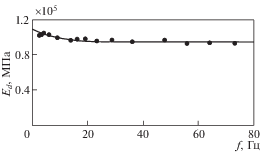
Полученные значения Ed имеют некоторый экспериментальный разброс (рис. 2 – точки). Для получения сглаживающей кривой использовалась аппроксимация
Параметры c1, c2, c3, c4 данной аппроксимации определялись минимизацией целевой функции
(4)
$H({{c}_{1}},{{c}_{2}},{{c}_{3}},{{c}_{4}}) = \sum\limits_i {{{{(1 - E_{{d,i}}^{*}{\text{/}}{{E}_{{d,i}}})}}^{2}}} ,$В результате получена зависимость
(5)
$\begin{gathered} {{E}_{d}}(f) = 9.472 \times {{10}^{4}}\exp ( - 2.156 \times {{10}^{{ - 8}}}f) + \\ + \;1.528 \times {{10}^{4}}\exp ( - 1.238 \times {{10}^{{ - 1}}}f), \\ \end{gathered} $Идентификация демпфирующих свойств сплава ОТ-4. Теоретические основы. При затухающих изгибных колебаниях тест-образца материал в любой точке поперечного сечения находится в состоянии циклического растяжения-сжатия. В этом случае демпфирующие свойства материала определяются логарифмическим декрементом колебаний (ЛДК) D, зависящим от амплитуды деформации ε0. Для представления зависимости D(ε0) предлагается использовать степенную функцию
Демпфирующие свойства тест-образца при колебаниях по низшей моде определяются ЛДК δ(А), зависящим от амплитуды колебаний А его свободного конца (зависимость δ(А) можно получить обработкой экспериментальной виброграммы затухающих изгибных колебаний тест-образца). Идентификация демпфирующих свойств материала состоит в отыскании параметров α- и β-функции (6) по имеющейся экспериментальной зависимости δ*(А) так, чтобы расчетные ЛДК тест-образца мало отличались от экспериментальных значений δ* при некотором заданном наборе амплитуд Aj ( j = = 1, 2, …, m) в диапазоне представления зависимости δ*(А). Для оценки результатов необходимо ввести норму невязки сравниваемых величин, например, в виде
Здесь F(α, β) – целевая функция, неявно зависящая от параметров α и β; $\delta _{j}^{{\text{*}}}$, ${{\delta }_{j}}$ – соответственно экспериментальные и расчетные ЛДК тест-образца при амплитудах Aj ( j = 1, 2, …, m).
Для нахождения минимума функции нескольких переменных обычно используют метод координатного или скорейшего спуска [11], где требуется вычислять частные производные от данной функции по каждой независимой переменной. Однако, при отсутствии явной зависимости F(α, β) частные производные $\partial F{\text{/}}\partial \alpha $ и $\partial F{\text{/}}\partial {\beta }$ необходимо определять численно. Поэтому предпочтительными будут прямые методы поиска нулевого порядка [11] (симплекс-метод, метод Хука–Дживса, метод Розенброка), не требующие вычисления отмеченных производных. Наиболее удобным является метод Хука–Дживса, который легко реализуется при любой размерности пространства поиска.
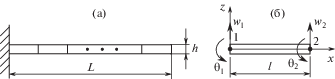
При моделировании затухающих изгибных колебаний тест-образца учитываются внутреннее демпфирование, обусловленное необратимым рассеянием энергии в материале, силы аэродинамического сопротивления и частотная зависимость динамического модуля упругости материала. Для учета комплекса перечисленных факторов предлагается использовать метод конечных элементов с представлением тест-образца совокупностью балочных элементов (рис. 3). Узловыми параметрами элемента являются прогибы w1, w2 и углы поворота поперечных сечений θ1, θ2, зависящие от времени t.
Представим прогиб w(t) в пределах элемента в виде
Здесь ${{r}_{e}}(t) = \{ {{w}_{1}}\;{{\theta }_{1}}\;{{w}_{2}}\;{{\theta }_{2}}\} $, $N = \{ {{N}_{1}}\;{{N}_{2}}\;{{N}_{3}}\;{{N}_{4}}\} $ – вектор базисных функций:
Для получения уравнений движения конечного элемента воспользуемся принципом Даламбера–Лагранжа
Здесь $\delta {{A}_{J}}$, $\delta {{A}_{\sigma }}$, $\delta {{A}_{a}}$ – соответственно возможные работы сил инерции, нормальных напряжений σ и сил аэродинамического сопротивления, определяемые с учетом представления (7). Символ δ в (8) и далее означает варьирование величины справа от него. Выражение для $\delta {{A}_{J}}$ получается следующим:
(9)
$\delta {{A}_{J}} = - m\int\limits_0^l {\delta w\ddot {w}dx} = - m\delta r_{e}^{T}\int\limits_0^l {N{{N}^{T}}} dx{{\ddot {r}}_{e}} = - \delta r_{e}^{T}{{M}_{e}}{{\ddot {r}}_{e}}.$Здесь m – погонная масса тест-образца, ${{M}_{e}}$ – матрица масс конечного элемента:
(10)
${{M}_{e}} = - m\int\limits_0^l {N{{N}^{T}}} dx = m\left[ {\begin{array}{*{20}{c}} {13l{\text{/}}35}&\vline & {11{{l}^{2}}{\text{/}}210}&\vline & {9l{\text{/}}70}&\vline & { - 13{{l}^{2}}{\text{/}}420} \\ \hline {11{{l}^{2}}{\text{/}}210}&\vline & {{{l}^{3}}{\text{/}}105}&\vline & {13{{l}^{2}}{\text{/}}420}&\vline & { - {{l}^{3}}{\text{/}}140} \\ \hline {9l{\text{/}}70}&\vline & {13{{l}^{2}}{\text{/}}420}&\vline & {13l{\text{/}}35}&\vline & { - 11{{l}^{2}}{\text{/}}210} \\ \hline { - 13{{l}^{2}}{\text{/}}420}&\vline & { - {{l}^{3}}{\text{/}}140}&\vline & { - 11{{l}^{2}}{\text{/}}210}&\vline & {{{l}^{3}}{\text{/}}105} \end{array}} \right].$Возможная работа $\delta {{A}_{\sigma }}$ зависит от модели неупругого деформирования материала. Если материал тест-образца обладает вязкоупругими свойствами, то для их описания можно использовать физические зависимости между компонентами тензора напряжений ${{\sigma }_{{ij}}}$, тензора деформаций ${{\varepsilon }_{{ij}}}$ и тензора скоростей деформаций ${{\dot {\varepsilon }}_{{ij}}}$ = $\partial {{\varepsilon }_{{ij}}}{\text{/}}\partial t$: ${{\sigma }_{{ij}}}$ = ${{\sigma }_{{ij}}}({{\varepsilon }_{{ij}}},{{\dot {\varepsilon }}_{{ij}}})$. При одноосном напряженном состоянии простейшая из таких зависимостей, наиболее часто используемая на практике, соответствует известной модели Фойгта–Томпсона–Кельвина [12, 13]
где σ, ε, $\dot {\varepsilon }$ – соответственно нормальное напряжение, относительная деформация и скорость ее изменения по времени t; E, η – модуль упругости и коэффициент вязкости материала. Коэффициент η связан с ЛДК D(ε0) материала зависимостью где ω – круговая частота деформирования материала. В случае зависимости упругих свойств материала от частоты ω, модуль E необходимо заменить динамическим модулем упругости Ed [14, 15]. С учетом такой замены и зависимости (12) модель (11) принимает видВ этом случае возможная работа $\delta {{A}_{\sigma }}$ будет такой
(13)
$\delta {{A}_{\sigma }} = - \int\limits_0^l {\int\limits_{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-0em} 2}}^{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2}} {\delta \varepsilon \sigma dzdx} } = - {{E}_{d}}b\left[ {\int\limits_0^l {\int\limits_{ - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2}}^{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2}} {\delta \varepsilon \varepsilon dzdx} + \frac{1}{{\pi \omega }}\int\limits_0^l {\int\limits_{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-0em} 2}}^{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2}} {\delta \varepsilon D({{\varepsilon }_{0}})\dot {\varepsilon }dzdx} } } } \right].$Деформация ε и ее амплитуда ε0 в точке z поперечного сечения элемента определяются геометрическими зависимостями
(14)
${\varepsilon } = - z{{(N{\text{'')}}}^{T}}{{r}_{e}},\quad {{{\varepsilon }}_{{\text{0}}}} = \left| z \right|{{{\chi }}_{0}}(x).$Здесь ${{{\chi }}_{0}}(x)$ – амплитуда кривизны оси элемента. Будем считать, что величина ${{{\chi }}_{0}}$ не зависит от x и равна ее значению в середине элемента. Тогда вместо (6) получается зависимость
Подставляя данную зависимость в выражение (13) и учитывая (14) получаем
Последнее выражение можно привести к виду
(15)
$\delta {{A}_{\sigma }} = - \delta r_{e}^{T}{{K}_{e}}{{r}_{e}} - \delta r_{e}^{T}{{C}_{{e,m}}}{{\dot {r}}_{e}},$(16)
$\begin{gathered} {{K}_{e}} = \frac{{{{E}_{d}}b{{h}^{3}}}}{{12}}\int\limits_0^l {N{\text{''}}{{{(N{\text{''}})}}^{T}}dx} = \frac{{{{E}_{d}}b{{h}^{3}}}}{{12}}\left[ {\begin{array}{*{20}{c}} {12{\text{/}}{{l}^{3}}}&\vline & {6{\text{/}}{{l}^{2}}}&\vline & { - 12{\text{/}}{{l}^{3}}}&\vline & {6{\text{/}}{{l}^{2}}} \\ \hline {6{\text{/}}{{l}^{2}}}&\vline & {4{\text{/}}l}&\vline & { - 6{\text{/}}{{l}^{2}}}&\vline & {2{\text{/}}l} \\ \hline { - 12{\text{/}}{{l}^{3}}}&\vline & { - 6{\text{/}}{{l}^{2}}}&\vline & {12{\text{/}}{{l}^{3}}}&\vline & { - 6{\text{/}}{{l}^{2}}} \\ \hline {6{\text{/}}{{l}^{2}}}&\vline & {2{\text{/}}l}&\vline & { - 6{\text{/}}{{l}^{2}}}&\vline & {4{\text{/}}l} \end{array}} \right]; \\ {{C}_{{e,m}}} = \frac{{3\alpha {{{({{\chi }_{0}}h{\text{/}}2)}}^{\beta }}}}{{\pi \omega (\beta + 3)}}{{K}_{e}}. \\ \end{gathered} $При определении сил аэродинамического сопротивления считается, что аэродинамическое взаимодействие может быть сведено к инерционному эффекту присоединенной массы и аэродинамическому демпфированию. Инерционный эффект приводит к снижению частоты, а аэродинамическое демпфирование – к росту ЛДК тест-образца по сравнению с его колебаниями в вакууме. Классической в этом случае является аппроксимация Морисона [7, 8]
(17)
${{P}_{a}}(x,t) = - 0.25{{\rho }_{a}}{{b}^{2}}{{C}_{M}}\dot {u} - 0.5{{\rho }_{a}}b{{C}_{D}}\left| u \right|u.$Здесь Pa(x, t) – погонная аэродинамическая сила, ρa – плотность воздуха, CM – коэффициент присоединенной массы; CD – коэффициент аэродинамического сопротивления, $u = \dot {w}$ – скорость потока относительно тест-образца на бесконечности. Коэффициенты CM и CD являются функциями безразмерных параметров ${{\kappa }_{0}} = A{\text{/}}b$, $d = {{b}^{2}}\omega {\text{/}}(2\pi \mu )$ и $\Delta = h{\text{/}}b$, где μ – кинематическая вязкость воздуха. В работе [4] показано, что при колебаниях тест-образца в воздухе влияние присоединенной массы на относительное снижение частоты ω (по сравнению с частотой в вакууме) составляет величину порядка 0,001. Поэтому далее этим влиянием можно пренебречь и вместо (17) использовать выражение
Коэффициент аэродинамического сопротивления обычно представляется в виде суммы вязкой Cvis и вихревой Cvort составляющих [4, 16]: CD = Cvis + Cvort. Влияние вязкой составляющей на ЛДК тест-образца существенно только на малых амплитудах колебаний. При этом можно использовать аналитическое приближение Стокса, из которого для тонкого тест-образца (Δ < 1/3) следует формула [17]
где $W(\xi )$ – нормированная низшая мода колебаний тест-образцаДля определения составляющей ${{C}_{{{\text{vort}}}}}$ можно воспользоваться аппроксимацией, приведенной в работе [6]
Перейдем к определению возможной работы погонной аэродинамической силы Pa(x, t) по длине конечного элемента. При этом будем считать, что величины CD и $\left| {\dot {w}} \right|$ в пределах элемента постоянны и равны их значениям в его середине
Подставляя сюда представление (7) получаем
С учетом равенства (10) и выражения для погонной массы m = ρbh последнее соотношение можно привести к виду
где ${{C}_{{e,a}}}$ – матрица аэродинамического демпфирования конечного элемента:(19)
${{C}_{{e,a}}} = 0.5{{\rho }_{a}}{{C}_{D}}\left| {\dot {w}} \right|{{M}_{e}}{\text{/}}({\rho }h).$Подставляя выражения (9), (15) и (18) в уравнение (8) и учитывая условие $\delta {{r}_{e}} \ne 0$, получаем систему уравнений движения конечного элемента
Объединяя данные уравнения по направлениям общих для смежных конечных элементов узловых перемещений приходим к системе разрешающих уравнений
где $M$, ${{С }_{m}}$, ${{С }_{a}}$, $K$, $r$ – соответственно матрица масс, матрицы внутреннего и аэродинамического демпфирования, матрица жесткости и вектор узловых перемещений конечно-элементной модели тест-образца. Необходимо заметить, что матрица $K$ в уравнениях (20) должна вычисляться при динамическом модуле упругости Ed, зависящим от расчетной частоты f, которая на момент формирования системы (20) еще неизвестна. Поэтому процесс определения частоты f необходимо итерировать [1] используя полученную зависимость (5). Однако, проведенные численные эксперименты показали, что поученная таким образом частота f оказывается довольно близкой к экспериментальной частоте ${{f}_{{\text{*}}}}$. Поэтому с целью сокращения трудоемкости вычисления матрицы $K$ динамический модуль Ed можно вычислять по зависимости (5) при экспериментальной частоте ${{f}_{{\text{*}}}}$.Из выражений (16) и (19) видно, что матрица ${{С }_{m}}$ должна зависеть от амплитуд кривизны χ0, а матрица ${{С }_{a}}$ – от модулей скоростей $\left| {\dot {w}} \right|$ центров конечных элементов. В этом случае уравнения (20) возможно решить только с использованием прямых шаговых методов с вычислением матрицы ${{С }_{a}}$ на каждом шаге интегрирования и пересчетом матрицы ${{С }_{m}}$ на каждом цикле колебаний, что приводит к высокой трудоемкости решения данных уравнений. В связи с этим вместо (19) предлагается использовать соотношение
Это дает возможность пересчитывать матрицу ${{С }_{a}}$ не на каждом шаге интегрирования, а так же как и матрицу ${{С }_{a}}$, на каждом цикле колебаний в соответствии с достигнутыми значениями w0 центров конечных элементов.
Так как затухающие колебания тест-образца происходят по низшей моде F, то справедливо представление r = Fq, где q – нормальная координата данной моды. Это дает возможность перейти от системы (20) к уравнению
с модальными параметрамиУравнение (22) дает возможность определить расчетные амплитуды затухающих колебаний и соответствующие им ЛДК тест-образца. При этом вместо шагового интегрирования возможно использовать алгоритм прогонки [18], значительно сокращающий процесс определения отмеченных параметров:
Модальные параметры $c_{{q,m}}^{{(i + 1)}}$ и $c_{{q,a}}^{{(i + 1)}}$ вычисляются при амплитуде колебаний A(i + 1) по соответствующим матрицам демпфирования Cm и Ca тест-образца. Необходимые для этого значения амплитуды кривизны ${\chi }_{0}^{{(i + 1)}}$ в серединах конечных элементов определяются выражением
Необходимо отметить, что зависимости $D({{\varepsilon }_{0}}) = \alpha \varepsilon _{0}^{\beta }$, найденные на различных тест-образцах, могут иметь значительный разброс. Поэтому данные зависимости необходимо определять на нескольких тест-образцах, усредняя после этого полученные результаты.
Численные эксперименты. Для идентификации параметров α и β зависимости $D({{\varepsilon }_{0}})$ = $\alpha \varepsilon _{0}^{\beta }$ титанового сплава ОТ-4 использовались экспериментальные ЛДК шести тест-образцов с длинами 150, 160, 175, 200, 225 и 250 мм. Толщина и ширина тест-образцов: h = 1.94 мм; b = 20 мм. Экспериментальные ЛДК тест-образцов определялись по известной формуле
Для представления аналитической зависимости огибающей $A(t)$ использовалась аппроксимация
с параметрами a1, a2, a3, a4, определяемыми из условияПоиск параметров α и β зависимости $D({{\varepsilon }_{0}}) = \alpha \varepsilon _{0}^{\beta }$ осуществлялся методом Хука–Дживса при координатах базовой точки
Таблица 2.
| L, м | α0 | β0 | α | β | r | F(α, β) |
|---|---|---|---|---|---|---|
| 150 | 0.01857 | 0.08089 | 0.01806 | 0.08080 | 145 | 0.000000147 |
| 160 | 0.04360 | 0.16632 | 0.04347 | 0.16932 | 110 | 0.000000143 |
| 175 | 0.06458 | 0.20759 | 0.05742 | 0.19347 | 900 | 0.000000779 |
| 200 | 0.06244 | 0.21456 | 0.04546 | 0.18345 | 2370 | 0.000000983 |
| 225 | 0.10381 | 0.26712 | 0.06198 | 0.21342 | 3365 | 0.000001494 |
| 250 | 0.04670 | 0.15051 | 0.01733 | 0.05223 | 7625 | 0.000003371 |
На рис. 4 для примера приведены экспериментальная (пунктирная линия) и расчетная (сплошная линия) амплитудные зависимости ЛДК тест-образца длиной L = 175 мм. Полученные зависимости являются достаточно близкими между собою, что свидетельствует о хорошем качестве поиска параметров α и β.
Рис. 4.
Амплитудные зависимости ЛДК тест-образца длиной L = 175 мм, экспериментальная (пунктирная линия) и расчетная (сплошная линия).
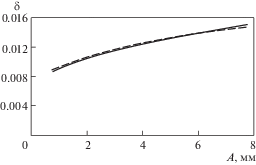
На рис. 5 приведены полный ЛДК (1), параметр внутреннего демпфирования (ПВД) (2), обусловленный демпфирующими свойствами материала и аэродинамическая составляющая демпфирования (3) тест-образца длиной L = 225 мм. Нетрудно видеть, что аэродинамическое сопротивление заметно увеличивает демпфирующие свойства тест-образца (по сравнению с ПВД), что говорит о необходимости учета данного сопротивления при идентификации демпфирующих свойств титанового сплава ОТ-4.
Рис. 5.
Полный ЛДК (1), ПВД (2) и аэродинамическая составляющая демпфирования (3) тест-образца длиной L = 225 мм.
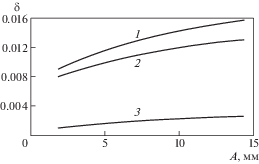
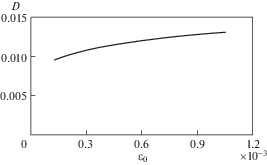
По параметрам α и β, приведенным в табл. 2, проведено арифметическое усреднение зависимостей $D({{\varepsilon }_{0}}) = \alpha \varepsilon _{0}^{\beta }$ в 50 точках рабочего диапазона амплитуд деформаций ε0 = [0.123 × 10–3; 1.056 × 10–3] с последующей идентификацией окончательной амплитудной зависимости ЛДК титанового сплава ОТ-4 по отмеченным точкам. В результате получена зависимость
показывающая заметное увеличение ЛДК отмеченного сплава при возрастании амплитуды деформации ε0 (рис. 6).Выводы. Показано снижение динамического модуля упругости титанового сплава ОТ-4 при растяжении–сжатии в диапазоне частот f = 0–25 по сравнению с его статическим номиналом (примерно на 13.3%) с дальнейшей практической стабилизацией отмеченного модуля при частотах 25–80 Гц, что необходимо учитывать при определении собственных частот колебаний и динамической напряженности элементов конструкций, изготовленных из данного сплава. Построена матрица аэродинамического демпфирования конечного элемента, позволяющая включить аэродинамическое сопротивление в расчетный ЛДК тест-образца при идентификации демпфирующих свойств материала. Получена усредненная зависимость ЛДК сплава ОТ-4 при растяжении-сжатии от амплитуды соответствующей деформации на основе исследования затухающих изгибных колебаний серии тест-образцов, показывающая заметное возрастание демпфирующих свойств отмеченного сплава при увеличении амплитуды деформации ε0.
Исследование выполнено за счет гранта Российского научного фонда (проект № 14-19-00667).
Список литературы
Paimushin V.N., Firsov V.A., Gynal I., Shishkin V.M. Accounting for the Frequency-Dependent Dynamic Elastic Modulus of Duralumin in Deformation Problems // J. Appl. Mech. and Tech. Phys. 2017. V. 58. № 3. P. 517–528.
ASTM E-756-05. Standard Test Method for Measuring Vibration-damping Properties of Materials. ASTM International, PA, 2010.
Paimushin V.N., Firsov V.A., Gunal I., Egorov A.G. Theoretical-Experimental Method for Determining the Parameters of Damping Based on the Study of Damped Flexural Vibrations of Test Specimens. 1. Experimental Basis // Mechanics of Composite Materials. 2014. V. 50. № 2. P. 127–136.
Egorov A.G., Kamalutdinov A.M., Nuriev A.N., Paimushin V.N. Theoretical-Experimental Method for Determining the Parameters of Damping Based on the Study of Damped Flexural Vibrations of Test Specimens. 2. Aerodynamic Component of Damping // Mechanics of Composite Materials. 2014. V. 50. № 3. P. 267–278.
Камалутдинов А.М., Егоров А.Г. Определение коэффициента аэродинамического сопротивления гармонически колеблющейся тонкой пластины / Сборник докладов XI Всероссийского съезда по фундаментальным проблемам теоретической и прикладной механики. Казань, 20–24 августа 2015 г. С. 1693–1695.
Egorov A.G., Kamalutdinov A.M., Paimushin V.N., Firsov V.A. Theoretical-Experimental Method of Determining the Drag Coefficient of a Harmonically Oscillating Thin Plate // J. Appl. Mech. and Tech. Phys. 2016. V. 57. № 2. P. 275–282.
Sarpkaya T. Force on a circular cylinder in viscous oscillatory flow at low Keulegan–Carpenter numbers // J. Fluid Mech. 1986. V. 165. P. 61–71.
Keulegan G.H., Carpenter L.H. Forces on cylinders and plates in an oscillating fluid. // J. Res. Nat. Bureau of Standards. 1958. V. 60. № 5. P. 423–440.
Писаренко Г.С., Яковлев А.П., Матвеев В.В. Вибропоглощающие свойства конструкционных материалов: Справочник. Киев: Наукова думка, 1971. 375 с.
Paimushin V.N., Firsov V.A., Gyunal I., Egorov A.G., Kayumov R.A. Theoretical-experimental Method for Determining the Parameters of Damping Based on the Study of Damped Flexural Vibrations of Test Specimens. 3. Identification of the Characteristics of Internal Damping // Mechanics of Composite Materials. 2014. V. 50. № 5. P. 633–646.
Шуп Т. Решение инженерных задач на ЭВМ. М.: Мир, 1982. 238 с.
Хильчевский В.В., Дубенец В.Г. Рассеяние энергии при колебаниях тонкостенных элементов конструкций // Киев: Вища школа, 1977. 252 с.
Постников В.С. Внутреннее трение в металлах. М.: Металлургия, 1969. 330 с.
Paimushin V.N., Firsov V.A., Gynal I., Shishkin V.M. Development of an Improved Technique for Identification of the Damping Properties of Orthogonally Reinforced Composites in Shear // Mechanics of Composite Materials. 2016. V. 52. № 2. P. 133–142.
Paimushin V.N., Firsov V.A., Gynal I., Shishkin V.M. Identification of the Elastic and Damping Characteristics of Soft Materials Based on the Analysis of Damped Flexural Vibrations of Test Specimens // Mechanics of Composite Materials. 2016. V. 52. № 4. P. 435–454.
Sader J.E. Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope // J. Appl. Phys. 1998. V. 84. № 1. P. 64–76.
Aureli M., Porfiri M. Low frequency and large amplitude oscillations of cantilevers in viscous fluids // Appl. Phys. Lett. 2010. V. 96. 164102.
Paimushin V.N., Firsov V.A., Gynal I., Shishkin V.M. Identification of the Elastic and Damping Characteristics of Carbon Fiber-Reinforced Plastic Based on a Study of Damping Flexsural Vibrations Test Specimens // J. Appl. Mech. and Tech. Phys. 2016. V. 57. № 4. P. 720–730.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин