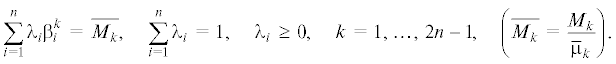Проблемы машиностроения и надежности машин, 2019, № 3, стр. 104-112

ФУНКЦИЯ ВОССТАНОВЛЕНИЯ ПРИ НАРАБОТКАХ С РАСПРЕДЕЛЕНИЯМИ КАК СМЕСЬ n ЭКСПОНЕНЦИАЛЬНЫХ РАСПРЕДЕЛЕНИЙ. НАХОЖДЕНИЕ ПАРАМЕТРОВ СМЕСЕЙ МЕТОДОМ МОМЕНТОВ

И. М. Федотова^1, *, В. И. Вайнштейн¹, Г. М. Цибульский¹, Ю. В. Вайнштейн¹

¹ Институт космических и информационных технологий ФГАОУ ВО “Сибирский федеральный университет”
Красноярск, Россия

Поступила в редакцию 27.10.2017
Принята к публикации 18.02.2019

DOI: 10.1134/S0235711919030040

Аннотация

В статье рассматриваются задачи теории надежности технических систем для случая, когда наработки до отказа восстанавливаемых (заменяемых) элементов распределены как смесь распределений. Для простого процесса восстановления, когда наработки распределены в виде смеси $n$ экспоненциальных распределений, представлен метод нахождения в явном виде функции восстановления (среднего числа отказов на промежутке от 0 до t). Для случая $n = 3$ выписана ее явная формула. Случай $n = 2$ рассмотрен в [1]. Для смесей двух и трех экспоненциальных, Эрланга, Релея и Максвелла распределений представлен алгоритм получения в явном виде точечных оценок неизвестных параметров, входящих в смесь. В работе продолжаются исследования, начатые в работах [1, 2].

Ключевые слова: смесь функций распределений, процесс восстановления, функция восстановления, метод моментов

1. Введение. Постановка задачи. Имеется большое количество известных законов распределения, например, экспоненциальное, Вейбулла–Гнеденко, Эрланга, гамма-распределение, нормальное, усеченное нормальное, логарифмически нормальное, обратное гауссовское, Релея, Максвелла, которым подчиняются наработки многих элементов различных технических систем [3]. Понятно, что все они не могут описать разнообразие наработок элементов при их эксплуатации. Например, плотности вероятности известных законов не более чем одномодальны, хотя у наработок плотности могут быть бимодальными (двухвершинными) и даже полимодальными, или когда функция распределения наработки до отказа является смесью двух или большего числа функций распределений из множества известных законов распределения.

Смесь $n$ функций распределений ${{F}_{i}}(t)$, $i = 1,\; \ldots ,\;n$ [3] определяется по формуле

(1)

$F(t) = \sum\limits_{i = 1}^n \,{{{\lambda }}_{i}}{{F}_{i}}(t),\quad {{{\lambda }}_{i}} \geqslant 0,\quad \sum\limits_{i = 1}^n \,{{{\lambda }}_{i}} = 1.$

В отличие от одной функции распределения, для смеси распределений задача нахождения точечных оценок параметров, входящих в смесь, значительно усложняется. Это связано со сложностью трансцендентной целевой функции правдоподобия для максимизации, если задача решается методом максимального правдоподобия, с большим количеством неизвестных параметров (к параметрам функций распределения, задающих смесь, добавляются неизвестные параметры ${{{\lambda }}_{i}}$ с дополнительными условиями ${{{\lambda }}_{i}} \geqslant 0$, $\sum\nolimits_{i = 1}^k {{{{\lambda }}_{i}}} $ = 1). Задача еще может усложниться за счет определения функций распределения, задающих смесь, и их количества. Это так называемая задача расщепления смеси [4–8].

В работе рассматриваются две задачи:

1. Нахождение функции восстановления (среднего числа отказов на промежутке от нуля до $t$) для простого процесса восстановления, образованного наработками, распределенными как смесь $n$ экспоненциальных распределений.

Простым (обычным) процессом восстановления называется последовательность неотрицательных независимых случайных величин ${{X}_{i}}$ – наработок элементов от $i - 1$-го до $i$-го отказа, имеющих одну и ту же функцию распределения [2, 3, 9–12].

2. Нахождение методом моментов точечных оценок неизвестных параметров, входящих в смесь распределений.

2. Функция восстановления простого процесса восстановления при наработках, распределенных как смесь n экспоненциальных распределений. Запишем функцию распределения и плотность смеси $n$ экспоненциальных распределений

(2)

$F(t) = \sum\limits_{i = 1}^n \,{{\lambda }_{i}}(1 - {{e}^{{ - {{\alpha }_{i}}t}}}),\quad f(t) = F{\kern 1pt} {\text{'}}(t) = \sum\limits_{i = 1}^n \,{{\lambda }_{i}}{{\alpha }_{i}}{{e}^{{ - {{\alpha }_{i}}t}}},\quad t \geqslant 0,\quad {{\lambda }_{i}} \geqslant 0,\quad \sum\limits_{i = 1}^n \,{{\lambda }_{i}} = 1.$

Исследуем функцию интенсивности отказов $\varphi (t)$ = $\frac{{f(t)}}{{1 - F(t)}}$ = $\frac{{\sum\nolimits_{i = 1}^n {{{\lambda }_{i}}{{\alpha }_{i}}{{e}^{{ - {{\alpha }_{i}}t}}}} }}{{\sum\nolimits_{i = 1}^n {{{\lambda }_{i}}{{e}^{{ - {{\alpha }_{i}}t}}}} }}$:

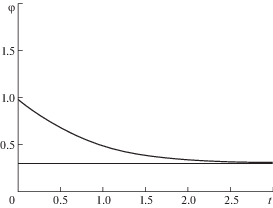
$\mathop {\lim }\limits_{t \to \infty } \,\varphi (t) = \mathop {\lim }\limits_{t \to \infty } \frac{{\sum\limits_{i = 1}^n \,{{\lambda }_{i}}{{\alpha }_{i}}{{e}^{{ - {{\alpha }_{i}}t}}}}}{{\sum\limits_{i = 1}^n {{\lambda }_{i}}{{e}^{{ - {{\alpha }_{i}}t}}}}} = \mathop {\lim }\limits_{t \to \infty } \frac{{{{\lambda }_{k}}{{\alpha }_{k}} + \sum\limits_{i = 1,i \ne k}^n {{\lambda }_{i}}{{e}^{{ - ({{\alpha }_{i}} - {{\alpha }_{k}})t}}}}}{{{{\lambda }_{k}} + \sum\limits_{i = 1,i \ne k}^n {{\lambda }_{i}}{{e}^{{ - ({{\alpha }_{i}} - {{\alpha }_{k}})t}}}}} = {{\alpha }_{k}} = \mathop {\min }\limits_{i = 1,2,...,n} {{\alpha }_{i}},$

$\varphi {\text{'}}(t) = \left( {\frac{{\sum\limits_{i = 1}^n \,{{\lambda }_{i}}{{\alpha }_{i}}{{e}^{{ - {{\alpha }_{i}}t}}}}}{{\sum\limits_{i = 1}^n \,{{\lambda }_{i}}{{e}^{{ - {{\alpha }_{i}}t}}}}}} \right)' = - \frac{{\sum\limits_{i = 1}^n \,\sum\limits_{j = 1,j \ne i}^n {{\lambda }_{i}}{{\lambda }_{j}}{{{({{\alpha }_{i}} - {{\alpha }_{j}})}}^{2}}{{e}^{{ - ({{\alpha }_{i}} + {{\alpha }_{j}})t}}}}}{{2{{{\left( {\sum\limits_{i = 1}^n \,{{\lambda }_{i}}{{e}^{{ - {{\alpha }_{i}}t}}}} \right)}}^{2}}}} < 0,\quad \varphi (0) = \sum\limits_{i = 1}^n \,{{\lambda }_{i}}{{\alpha }_{i}}.$

Получили, что функция интенсивности отказов монотонно убывает, и прямая $\varphi = {{\alpha }_{k}}$ является ее горизонтальной асимптотой. Характерный график функции интенсивности отказов имеет вид (рис. 1).

Рис. 1.

Замечание. Интенсивность отказов экспоненциального распределения F(t) = 1 – ${{e}^{{ - \alpha t}}}$ постоянна: $\varphi (t) = \alpha $. Из рис. 1 видно, что интенсивность отказов смеси экспоненциальных распределений имеет период приработочных отказов, и лишь с увеличением продолжительности работы интенсивность становится практически постоянной. Это существенно отличает смесь экспоненциальных распределений от одного экспоненциального распределения, при котором интенсивность отказов не имеет периода приработки, такого важного и характерного в начальный период работы многих технических систем.

Найдем функцию восстановления $H(t)$ (среднее число отказов за время от нуля до $t$) простого процесса восстановления, образованного смесью $n$ экспоненциальных распределений. Запишем интегральное уравнение для функции восстановления [2, 3, 9–12]

$H(t) = F(t) + \int\limits_0^t {H(t - x)dF(x)} .$

Для (2)

(3)

$H(t) = \sum\limits_{i = 1}^n {{{\lambda }_{i}}(1 - {{e}^{{ - {{\alpha }_{i}}t}}})} + \int\limits_0^t {H(t - x)d\left( {\sum\limits_{i = 1}^n {{{\lambda }_{i}}(1 - {{e}^{{ - {{\alpha }_{i}}x}}})} } \right)} .$

Переходя в (3) к преобразованию Лапласа–Стилтьеса $F{\text{*}}(s)$ = $\int_0^\infty {{{e}^{{ - st}}}dF(t)} $ [3, 11] и, учитывая ${\text{(}}1 - {{e}^{{ - {{\alpha }_{i}}t}}}{\text{)*}}(s)$ = $\frac{{{{\alpha }_{i}}}}{{s + {{\alpha }_{i}}}}$, ${\text{(}}\int_0^t {H(t - x)dF(x)} {\text{)*}}(s)$ = $H{\text{*}}(s)F{\text{*}}(s)$ [3], получаем $H{\text{*}}(s)$ = = $\sum\nolimits_{i = 1}^n {\frac{{{{\lambda }_{i}}{{\alpha }_{i}}}}{{s + {{\alpha }_{i}}}}} $ + $H{\text{*}}(s)\sum\nolimits_{i = 1}^n {\frac{{{{\lambda }_{i}}{{\alpha }_{i}}}}{{s + {{\alpha }_{i}}}}} $. Отсюда

(4)

$H{\text{*}}(s) = \frac{{\sum\limits_{i = 1}^n \frac{{{{\lambda }_{i}}{{\alpha }_{i}}}}{{s + {{\alpha }_{i}}}}}}{{1 - \sum\limits_{i = 1}^n \frac{{{{\lambda }_{i}}{{\alpha }_{i}}}}{{s + {{\alpha }_{i}}}}}} = \frac{{\sum\limits_{i = 1}^n {{\lambda }_{i}}{{\alpha }_{i}}\prod\limits_{j = 1,j \ne i}^n (s + {{\alpha }_{j}})}}{{\prod\limits_{i = 1}^n (s + {{\alpha }_{i}}) - \sum\limits_{i = 1}^n {{\lambda }_{i}}{{\alpha }_{i}}\prod\limits_{j = 1,j \ne i}^n (s + {{\alpha }_{j}})}} = \frac{{{{P}_{{n - 1}}}(s)}}{{{{Q}_{n}}(s)}},$

${{P}_{{n - 1}}}(s)$, ${{Q}_{n}}(s)$ – многочлены степени $n - 1$ и $n$ соответственно

${{P}_{{n - 1}}}(0) = \sum\limits_{i = 1}^n \,{{\lambda }_{i}}\,\prod\limits_{j = 1}^n {{\alpha }_{j}} = 1 \cdot \prod\limits_{j = 1}^n \,{{\alpha }_{j}} \ne 0,$

${{Q}_{n}}(0) = \prod\limits_{i = 1}^n \,{{\alpha }_{i}} - \sum\limits_{i = 1}^n \,{{\lambda }_{i}}\,\prod\limits_{j = 1}^n \,{{\alpha }_{j}} = \prod\limits_{i = 1}^n \,{{\alpha }_{i}} - 1 \cdot \prod\limits_{j = 1}^n \,{{\alpha }_{j}} = 0.$

Переходя к обратному преобразованию Лапласа–Стилтьеса в (4), находим функцию восстановления $H(t)$. Для нахождения обратного преобразования Лапласа–Стилтьеса следует вначале перейти к преобразованию Лапласа [2, 13]

(5)

$\hat {H}(s) = \int\limits_0^\infty {{{e}^{{ - st}}}H(t)dt} ,\quad \hat {H}(s) = \frac{{H{\text{*}}(s)}}{s},$

а затем воспользоваться формулой обратного преобразования Лапласа дробно-рациональной функции.

Если $\hat {H}(s)$ дробно-рациональная функция: $\hat {H}(s) = \frac{{{{P}_{m}}(s)}}{{{{Q}_{n}}(s)}}$, ${{P}_{m}}(s)$, ${{Q}_{n}}(s)$ – многочлены степени $m$ и $n$ соответственно ($m < n$), то [13]

(6)

$H(t) = \sum\limits_{k = 1}^r \frac{1}{{({{l}_{k}} - 1)!}}\mathop {lim}\limits_{s \to {{s}_{k}}} \frac{{{{d}^{{{{l}_{k}} - 1}}}}}{{d{{s}^{{{{l}_{k}} - 1}}}}}((s - {{s}_{k}}{{)}^{{{{l}_{k}}}}}\hat {H}(s){{e}^{{st}}}),$

где ${{s}_{k}}$ нули знаменателя функции $\hat {H}(s)$ кратности ${{l}_{k}}$ (${{Q}_{n}}({{s}_{k}}) = 0$), $k = 1,\; \ldots ,\;r$, $\sum\nolimits_{k = 1}^r {{{l}_{k}}} $ = n.

Рассмотрим случай $n = 3$. В соответствии с (4)

$H{\text{*}}(s)\, = \,\frac{{({{\lambda }_{1}}{{\alpha }_{1}}\, + {{\lambda }_{2}}{{\alpha }_{2}}\, + {{\lambda }_{3}}{{\alpha }_{3}}){{s}^{2}}\, + ({{\lambda }_{1}}{{\alpha }_{1}}({{\alpha }_{2}}\, + {{\alpha }_{3}}) + {{\lambda }_{2}}{{\alpha }_{2}}({{\alpha }_{1}}\, + {{\alpha }_{3}}) + {{\lambda }_{3}}{{\alpha }_{3}}({{\alpha }_{1}}\, + {{\alpha }_{2}}))s + {{\alpha }_{1}}{{\alpha }_{2}}{{\alpha }_{3}}}}{{s({{s}^{2}} + ({{\alpha }_{1}}(1 - {{\lambda }_{1}}) + {{\alpha }_{2}}(1 - {{\lambda }_{2}}) + {{\alpha }_{3}}(1 - {{\lambda }_{3}}))s + {{\lambda }_{3}}{{\alpha }_{1}}{{\alpha }_{2}} + {{\lambda }_{2}}{{\alpha }_{1}}{{\alpha }_{3}} + {{\lambda }_{1}}{{\alpha }_{2}}{{\alpha }_{3}})}}.$

При конкретных значениях параметров ${{\lambda }_{1}}$, ${{\lambda }_{2}}$, ${{\lambda }_{3}}$, ${{\alpha }_{1}}$, ${{\alpha }_{2}}$, ${{\alpha }_{3}}$ находим корни квадратного уравнения

${{s}^{2}} + ({{\alpha }_{1}}(1 - {{\lambda }_{1}}) + {{\alpha }_{2}}(1 - {{\lambda }_{2}}) + {{\alpha }_{3}}(1 - {{\lambda }_{3}}))s + {{\lambda }_{3}}{{\alpha }_{1}}{{\alpha }_{2}} + {{\lambda }_{2}}{{\alpha }_{1}}{{\alpha }_{3}} + {{\lambda }_{1}}{{\alpha }_{2}}{{\alpha }_{3}} = 0,$

а затем по формулам (5), (6) получаем функцию восстановления $H(t)$.

Для смеси двух экспоненциальных распределений $F(t)$ = $\lambda (1 - {{e}^{{ - {{\alpha }_{1}}t}}})$ + $(1 - \lambda )(1$ – ‒ ${{e}^{{ - {{\alpha }_{2}}t}}})$, $0 \leqslant \lambda \leqslant 1$, функция восстановления найдена в [1]

$H(t) = \frac{{{{\alpha }_{1}}{{\alpha }_{2}}}}{{(1 - \lambda ){{\alpha }_{1}} + \lambda {{\alpha }_{2}}}}t + \frac{{\lambda (1 - \lambda )({{\alpha }_{1}} - {{\alpha }_{2}}{{)}^{2}}}}{{{{{((1 - \lambda ){{\alpha }_{1}} + \lambda {{\alpha }_{2}})}}^{2}}}}(1 - {{e}^{{ - ((1 - \lambda ){{\alpha }_{1}} + \lambda {{\alpha }_{2}})t}}}).$

3. Метод моментов получения точечных оценок неизвестных параметров смеси распределений. Получим методом моментов явные формулы точечных оценок неизвестных параметров смеси двух и трех распределений характерных для теории надежности технических систем.

Пусть $F(t,{{\alpha }_{1}},{{\alpha }_{2}},\; \ldots ,\;{{\alpha }_{r}})$ – функция распределения, ${{\alpha }_{1}},{{\alpha }_{2}},\; \ldots ,\;{{\alpha }_{r}}$ – неизвестные параметры. Точечные оценки параметров находятся методом моментов приравнивая теоретические ${{\mu }_{k}}$ = $\int_0^\infty {{{x}^{k}}dF} (x,{{\alpha }_{1}},{{\alpha }_{2}},\; \ldots ,\;{{\alpha }_{r}})$ и эмпирические моменты ${{M}_{k}}$ = $\frac{1}{N}\sum\nolimits_{i = 1}^N {x_{i}^{k}} $ до порядка r, где ${{x}_{1}},{{x}_{2}},\; \ldots ,\;{{x}_{N}}$ – заданная выборка объема $N$

(7)

$\int\limits_0^\infty {{{x}^{k}}dF(x,{{\alpha }_{1}},{{\alpha }_{2}},\; \ldots ,\;{{\alpha }_{r}})} = \frac{1}{N}\sum\limits_{i = 1}^N \,x_{i}^{k},\quad k = 1,\; \ldots ,\;r.$

Систему (7) для смесей $n$ однопараметрических распределений Релея, Максвелла, Эрланга, экспоненциально можно записать в единообразном виде

(8)

1) Для смеси распределений Релея: ${{f}_{i}}(t)$ = $\left\{ {\begin{array}{*{20}{l}} {\frac{t}{{\sigma _{i}^{2}}}{{e}^{{ - \frac{{{{t}^{2}}}}{{2\sigma _{i}^{2}}}}}},\quad t \geqslant 0,} \\ {0,\quad t < 0,} \end{array}} \right.$ ${{\bar {\mu }}_{k}}$ = $\frac{{k!!}}{2}\sqrt {2\pi } $, если $k$ – нечетное и ${{\bar {\mu }}_{k}}$ = $\left( {\frac{k}{2}} \right){{!2}^{{\frac{k}{2}}}}$, если $k$ – четное, ${{\beta }_{i}} = {{\sigma }_{i}}$;

2) Для смеси распределений Максвелла: ${{f}_{i}}(t)$ = $\left\{ {\begin{array}{*{20}{l}} {\frac{{4h_{i}^{3}}}{{\sqrt \pi }}{{t}^{2}}{{e}^{{ - h_{i}^{2}{{t}^{2}}}}},\quad t \geqslant 0,} \\ {0,\quad t < 0,} \end{array}} \right.$ ${{\bar {\mu }}_{k}}$ = $\frac{2}{{\sqrt \pi }}\left( {\frac{{k + 1}}{2}} \right)!$, если $k$ – нечетное и ${{\bar {\mu }}_{k}}$ = $\frac{{(k + 1)!!}}{{{{2}^{{\frac{k}{2}}}}}}$, если $k$ – четное, ${{\beta }_{i}} = \frac{1}{{{{h}_{i}}}}$;

3) Для смеси распределений Эрланга порядка $m > 1$: ${{f}_{i}}(t)$ = $\frac{{\alpha _{i}^{m}{{t}^{{m - 1}}}}}{{(m - 1)!}}{{e}^{{ - {{\alpha }_{i}}t}}}$, ${{\bar {\mu }}_{k}}$ = m(m + + 1)...(m + k – 1), ${{\beta }_{i}} = \frac{1}{{{{\alpha }_{i}}}}$. При $m = 1$ имеем смесь $n$ экспоненциальных распределений.

Заметим, что система (8) является системой алгебраических уравнений относительно неизвестных ${{\lambda }_{i}}$, ${{\beta }_{i}}$. Это позволяет для ее решения эффективно применять различные пакеты прикладных программ, например, Maple. Это могут быть явные решения, либо решения, получаемые численными методами.

Для смесей двух и трех распределений: экспоненциальных, Релея, Максвелла и Эрланга решение системы (8) можно выписать в явном виде.

Запишем систему (8) для смеси двух распределений (${{\lambda }_{1}} = \lambda $, ${{\lambda }_{2}} = 1 - \lambda $)

(9)

$\lambda {{\beta }_{1}} + (1 - \lambda ){{\beta }_{2}} = {{\bar {M}}_{1}},\quad \lambda \beta _{1}^{2} + (1 - \lambda )\beta _{2}^{2} = {{\bar {M}}_{2}},\quad \lambda \beta _{1}^{3} + (1 - \lambda )\beta _{2}^{3} = {{\bar {M}}_{3}}.$

Из первого уравнения системы (9) выражаем $\lambda = \frac{{{{{\bar {M}}}_{1}} - {{\beta }_{2}}}}{{{{\beta }_{1}} - {{\beta }_{2}}}}$ и подставляем его во второе и третье уравнения

${{\bar {M}}_{1}}({{\beta }_{1}} + {{\beta }_{2}}) - {{\beta }_{1}}{{\beta }_{2}} = {{\bar {M}}_{2}},\quad {{\bar {M}}_{1}}{{({{\beta }_{1}} + {{\beta }_{2}})}^{2}} - {{\bar {M}}_{1}}{{\beta }_{1}}{{\beta }_{2}} - {{\beta }_{1}}{{\beta }_{2}}({{\beta }_{1}} + {{\beta }_{2}}) = {{\bar {M}}_{3}}.$

Переходя к неизвестным $p = {{\beta }_{1}} + {{\beta }_{2}}$ и $q = {{\beta }_{1}}{{\beta }_{2}}$, получаем линейную систему уравнений: ${{\bar {M}}_{1}}p - q$ = ${{\bar {M}}_{2}}$, ${{\bar {M}}_{2}}p$ – ${{\bar {M}}_{1}}q$ = ${{\bar {M}}_{3}}$. Ее решение:

$p = \frac{{{{{\bar {M}}}_{3}} - {{{\bar {M}}}_{1}}{{{\bar {M}}}_{2}}}}{{{{{\bar {M}}}_{2}} - \bar {M}_{1}^{2}}},\quad q = \frac{{{{{\bar {M}}}_{1}}{{{\bar {M}}}_{3}} - \bar {M}_{2}^{2}}}{{{{{\bar {M}}}_{2}} - \bar {M}_{1}^{2}}}.$

Далее по найденным ${{\beta }_{1}} = \frac{{p + \sqrt {{{p}^{2}} - 4q} }}{2}$, ${{\beta }_{2}} = \frac{{p - \sqrt {{{p}^{2}} - 4q} }}{2}$ находим неизвестные параметры смеси в явном виде.

Замечание. Если для конкретной выборки найденные решения комплексные, или хотя бы одно из них неположительное, или найденное $\lambda $ не удовлетворяет неравенству $0 \leqslant \lambda \leqslant 1$, то метод моментов для данной выборки не дает возможность получить точечные оценки неизвестных параметров смеси.

Явные формулы точечных оценок параметров для смеси двух экспоненциальных распределений получены в работе [1], включающей пример выборки, для которой гипотеза об экспоненциальном распределении отвергается, а гипотеза о распределении как смесь двух экспоненциальных согласуется с рассматриваемой выборкой.

Рассмотрим систему (8) для смеси трех распределений Релея, Максвелла, Эрланга:

${{\lambda }_{1}} + {{\lambda }_{2}} + {{\lambda }_{3}} = 1,\quad {{\lambda }_{1}}{{\beta }_{1}} + {{\lambda }_{2}}{{\beta }_{2}} + {{\lambda }_{3}}{{\beta }_{3}} = {{\bar {M}}_{1}},\quad {{\lambda }_{1}}\beta _{1}^{2} + {{\lambda }_{2}}\beta _{2}^{2} + {{\lambda }_{3}}\beta _{3}^{2} = {{\bar {M}}_{2}},$

${{\lambda }_{1}}\beta _{1}^{3} + {{\lambda }_{2}}\beta _{2}^{3} + {{\lambda }_{3}}\beta _{3}^{3} = {{\bar {M}}_{3}},\quad {{\lambda }_{1}}\beta _{1}^{4} + {{\lambda }_{2}}\beta _{2}^{4} + {{\lambda }_{3}}\beta _{3}^{4} = {{\bar {M}}_{4}},\quad {{\lambda }_{1}}\beta _{1}^{5} + {{\lambda }_{2}}\beta _{2}^{5} + {{\lambda }_{3}}\beta _{3}^{5} = {{\bar {M}}_{5}}.$

Из первых трех уравнений системы выражаем ${{\lambda }_{1}}$, ${{\lambda }_{2}}$, ${{\lambda }_{3}}$:

${{\lambda }_{1}} = \frac{{{{{\bar {M}}}_{1}}{{\beta }_{3}} - {{\beta }_{2}}{{\beta }_{3}} - {{{\bar {M}}}_{2}} + {{{\bar {M}}}_{1}}{{\beta }_{2}}}}{{({{\beta }_{1}} - {{\beta }_{2}})({{\beta }_{3}} - {{\beta }_{1}})}},\quad {{\lambda }_{2}} = - \frac{{{{{\bar {M}}}_{1}}{{\beta }_{3}} - {{\beta }_{1}}{{\beta }_{3}} - {{{\bar {M}}}_{2}} + {{{\bar {M}}}_{1}}{{\beta }_{1}}}}{{({{\beta }_{1}} - {{\beta }_{2}})({{\beta }_{3}} - {{\beta }_{2}})}},$

${{\lambda }_{3}} = - \frac{{{{{\bar {M}}}_{1}}{{\beta }_{1}} - {{\beta }_{1}}{{\beta }_{2}} - {{{\bar {M}}}_{2}} + {{{\bar {M}}}_{1}}{{\beta }_{2}}}}{{({{\beta }_{3}} - {{\beta }_{1}})({{\beta }_{3}} - {{\beta }_{2}})}}.$

Подставляем найденные ${{\lambda }_{1}}$, ${{\lambda }_{2}}$, ${{\lambda }_{3}}$ в четвертое, пятое и шестое уравнения системы. Имеем

${{\bar {M}}_{2}}({{\beta }_{1}} + {{\beta }_{2}} + {{\beta }_{3}}) - {{\bar {M}}_{1}}({{\beta }_{1}}{{\beta }_{2}} + {{\beta }_{2}}{{\beta }_{3}} + {{\beta }_{1}}{{\beta }_{3}}) + {{\beta }_{1}}{{\beta }_{2}}{{\beta }_{3}} = {{\bar {M}}_{3}},$

${{\bar {M}}_{2}}{{({{\beta }_{1}} + {{\beta }_{2}} + {{\beta }_{3}})}^{2}} - {{\bar {M}}_{1}}({{\beta }_{1}} + {{\beta }_{2}} + {{\beta }_{3}})({{\beta }_{1}}{{\beta }_{2}} + {{\beta }_{2}}{{\beta }_{3}} + {{\beta }_{1}}{{\beta }_{3}}) + {{\beta }_{1}}{{\beta }_{2}}{{\beta }_{3}}({{\beta }_{1}} + {{\beta }_{2}} + {{\beta }_{3}}) + $

$ + \;{{\bar {M}}_{1}}{{\beta }_{1}}{{\beta }_{2}}{{\beta }_{3}} - {{\bar {M}}_{2}}({{\beta }_{1}}{{\beta }_{2}} + {{\beta }_{2}}{{\beta }_{3}} + {{\beta }_{1}}{{\beta }_{3}}) = {{\bar {M}}_{4}},$

${{\bar {M}}_{2}}{{({{\beta }_{1}} + {{\beta }_{2}} + {{\beta }_{3}})}^{3}} - {{\bar {M}}_{1}}{{({{\beta }_{1}} + {{\beta }_{2}} + {{\beta }_{3}})}^{2}}({{\beta }_{1}}{{\beta }_{2}} + {{\beta }_{2}}{{\beta }_{3}} + {{\beta }_{1}}{{\beta }_{3}}) + {{\beta }_{1}}{{\beta }_{2}}{{\beta }_{3}}{{({{\beta }_{1}} + {{\beta }_{2}} + {{\beta }_{3}})}^{2}} + $

$ + \;{{\bar {M}}_{1}}{{({{\beta }_{1}}{{\beta }_{2}} + {{\beta }_{2}}{{\beta }_{3}} + {{\beta }_{1}}{{\beta }_{3}})}^{2}} + {{\bar {M}}_{1}}{{\beta }_{1}}{{\beta }_{2}}{{\beta }_{3}}({{\beta }_{1}} + {{\beta }_{2}} + {{\beta }_{3}}) - {{\beta }_{1}}{{\beta }_{2}}{{\beta }_{3}}({{\beta }_{1}}{{\beta }_{2}} + {{\beta }_{2}}{{\beta }_{3}} + {{\beta }_{1}}{{\beta }_{3}}) - $

$ - \;{{\bar {M}}_{2}}({{\beta }_{1}} + {{\beta }_{2}} + {{\beta }_{3}})({{\beta }_{1}}{{\beta }_{2}} + {{\beta }_{2}}{{\beta }_{3}} + {{\beta }_{1}}{{\beta }_{3}}) + {{\bar {M}}_{2}}{{\beta }_{1}}{{\beta }_{2}}{{\beta }_{3}} = {{\bar {M}}_{5}}.$

Левые части полученной системы уравнений являются симметрическими многочленами, что дает возможность в переменных ${{\beta }_{1}} + {{\beta }_{2}} + {{\beta }_{3}} = p$, ${{\beta }_{1}}{{\beta }_{2}} + {{\beta }_{1}}{{\beta }_{3}} + {{\beta }_{2}}{{\beta }_{3}} = q$ и ${{\beta }_{1}}{{\beta }_{2}}{{\beta }_{3}} = s$ преобразовать ее в линейную систему уравнений

${{\bar {M}}_{2}}p - {{\bar {M}}_{1}}q + s = {{\bar {M}}_{3}},\quad {{\bar {M}}_{3}}p - {{\bar {M}}_{2}}q + {{\bar {M}}_{1}}s = {{\bar {M}}_{4}},\quad {{\bar {M}}_{4}}p - {{\bar {M}}_{3}}q + {{\bar {M}}_{2}}s = {{\bar {M}}_{5}}.$

Ее решение:

$p = \frac{{{{{\bar {M}}}_{5}}\bar {M}_{1}^{2} - {{{\bar {M}}}_{5}}{{{\bar {M}}}_{2}} + \bar {M}_{2}^{2}{{{\bar {M}}}_{3}} + {{{\bar {M}}}_{3}}{{{\bar {M}}}_{4}} - {{{\bar {M}}}_{1}}\bar {M}_{3}^{2} - {{{\bar {M}}}_{2}}{{{\bar {M}}}_{1}}{{{\bar {M}}}_{4}}}}{{ - 2{{{\bar {M}}}_{2}}{{{\bar {M}}}_{1}}{{{\bar {M}}}_{3}} + \bar {M}_{2}^{3} + \bar {M}_{3}^{2} + \bar {M}_{1}^{2}{{{\bar {M}}}_{4}} - {{{\bar {M}}}_{2}}{{{\bar {M}}}_{4}}}},$

$q = - \frac{{{{{\bar {M}}}_{1}}{{{\bar {M}}}_{3}}{{{\bar {M}}}_{4}} - {{{\bar {M}}}_{1}}{{{\bar {M}}}_{5}}{{{\bar {M}}}_{2}} + {{{\bar {M}}}_{3}}{{{\bar {M}}}_{5}} - \bar {M}_{4}^{2} - \bar {M}_{3}^{2}{{{\bar {M}}}_{2}} + \bar {M}_{2}^{2}{{{\bar {M}}}_{4}}}}{{ - 2{{{\bar {M}}}_{2}}{{{\bar {M}}}_{1}}{{{\bar {M}}}_{3}} + \bar {M}_{2}^{3} + \bar {M}_{3}^{2} + \bar {M}_{1}^{2}{{{\bar {M}}}_{4}} - {{{\bar {M}}}_{2}}{{{\bar {M}}}_{4}}}},$

$s = \frac{{\bar {M}_{3}^{3} - 2{{{\bar {M}}}_{3}}{{{\bar {M}}}_{2}}{{{\bar {M}}}_{4}} - {{{\bar {M}}}_{1}}{{{\bar {M}}}_{3}}{{{\bar {M}}}_{5}} + {{{\bar {M}}}_{1}}\bar {M}_{4}^{2} + \bar {M}_{2}^{2}{{{\bar {M}}}_{5}}}}{{ - 2{{{\bar {M}}}_{2}}{{{\bar {M}}}_{1}}{{{\bar {M}}}_{3}} + \bar {M}_{2}^{3} + \bar {M}_{3}^{2} + \bar {M}_{1}^{2}{{{\bar {M}}}_{4}} - {{{\bar {M}}}_{2}}{{{\bar {M}}}_{4}}}}.$

По теореме Виета неизвестные ${{\beta }_{1}}$, ${{\beta }_{2}}$, ${{\beta }_{3}}$ являются корнями кубического уравнения ${{\beta }^{3}} - p{{\beta }^{2}} + q\beta - s = 0$. Отсюда

${{\beta }_{1}} = \frac{1}{6}{{A}^{{1/3}}} - 6B + \frac{1}{3}p,\quad {{\beta }_{2}} = - \frac{1}{{12}}{{A}^{{1/3}}} + 3B + \frac{1}{3}p + \frac{{\sqrt 3 }}{2}\left( {\frac{1}{6}{{A}^{{1/3}}} - 6B} \right)i,$

${{\beta }_{3}} = - \frac{1}{{12}}{{A}^{{1/3}}} + 3B + \frac{1}{3}p - \frac{{\sqrt 3 }}{2}\left( {\frac{1}{6}{{A}^{{1/3}}} - 6B} \right)i,$

где $A = - 36pq + 108s + 8{{p}^{3}}$ + $12\sqrt {12{{q}^{3}} - 3{{q}^{2}}{{p}^{2}} - 54pqs + 81{{s}^{2}} + 12s{{p}^{3}}} $, $B = \frac{{3q - {{p}^{2}}}}{{9{{A}^{{1/3}}}}}$.

Далее по найденным ${{\beta }_{1}}$, ${{\beta }_{2}}$, ${{\beta }_{3}}$ находим неизвестные параметры смеси в явном виде.

Рассмотрим смесь двух нормальных распределений

$f(t) = \lambda \frac{1}{{\sqrt {2\pi } {{\sigma }_{1}}}}{{e}^{{ - \frac{{{{{(t - {{a}_{1}})}}^{2}}}}{{2\sigma _{1}^{2}}}}}} + (1 - \lambda )\frac{1}{{\sqrt {2\pi } {{\sigma }_{2}}}}{{e}^{{ - \frac{{{{{(t - {{a}_{2}})}}^{2}}}}{{2\sigma _{2}^{2}}}}}},\quad {{\mu }_{{ik}}} = \frac{1}{{\sqrt {2\pi } {{\sigma }_{1}}}}\int\limits_{ - \infty }^\infty {{{t}^{k}}{{e}^{{ - \frac{{{{{(t - {{a}_{1}})}}^{2}}}}{{2\sigma _{1}^{2}}}}}}} dt,\quad k = 1,\; \ldots ,\;5,$

${{\mu }_{{i1}}} = {{a}_{i}},\quad {{\mu }_{{i2}}} = \sigma _{i}^{2} + a_{i}^{2},\quad {{\mu }_{{i3}}} = \sigma _{i}^{2}{{a}_{i}} + a_{i}^{3},\quad {{\mu }_{{i4}}} = 3\sigma _{i}^{4} + 6\sigma _{i}^{2}a_{i}^{2} + a_{i}^{4},$

${{\mu }_{{i5}}} = 15\sigma _{i}^{4}{{a}_{i}} + 10\sigma _{i}^{2}a_{i}^{3} + a_{i}^{5}.$

Для рассматриваемого случая система (8) запишется в виде

$\lambda {{a}_{1}} + (1 - \lambda ){{a}_{2}} = {{M}_{1}},\quad \lambda (\sigma _{1}^{2} + a_{1}^{2}) + (1 - \lambda )(\sigma _{2}^{2} + a_{2}^{2}) = {{M}_{2}},$

(10)

$\begin{gathered} \lambda (3\sigma _{1}^{2}{{a}_{1}} + a_{1}^{3}) + (1 - \lambda )(3\sigma _{2}^{2}{{a}_{2}} + a_{2}^{3}) = {{M}_{3}}, \\ \lambda (3\sigma _{1}^{4} + 6\sigma _{1}^{2}a_{1}^{2} + a_{1}^{4}) + (1 - \lambda )(3\sigma _{2}^{4} + 6\sigma _{2}^{2}a_{2}^{2} + a_{2}^{4}) = {{M}_{4}}, \\ \end{gathered} $

$\lambda (15\sigma _{1}^{4}{{a}_{1}} + 10\sigma _{1}^{2}a_{1}^{3} + a_{1}^{5}) + (1 - \lambda )(15\sigma _{2}^{4}{{a}_{2}} + 10\sigma _{2}^{2}a_{2}^{3} + a_{2}^{5}) = {{M}_{5}}.$

Укажем схему численного решения системы (10). Выражаем $\lambda $ из первого уравнения системы (10) и подставляем его во второе и третье уравнения. Относительно $\sigma _{1}^{2}$ и $\sigma _{2}^{2}$ получается линейная система двух уравнений. Из нее в явном виде $\sigma _{1}^{2}$ и $\sigma _{2}^{2}$ выражаются через ${{a}_{1}}$ и ${{a}_{2}}$. Найденные выражения для $\lambda $, $\sigma _{1}^{2}$, $\sigma _{2}^{2}$ подставляем в четвертое и пятое уравнения рассматриваемой системы (10). Получаем систему двух уравнений относительно ${{a}_{1}}$, ${{a}_{2}}$. Далее подстановкой $p = {{a}_{1}} + {{a}_{2}}$, $q = {{a}_{1}}{{a}_{2}}$ понижаем ее порядок. Указанные преобразования можно проводить в системе Maple.

В итоге система (10) сводится к системе двух алгебраических уравнений относительно p и q, которую численно решаем, например, в системе Maple.

Здесь, как и в выше рассмотренных случаях следует следить за выполнением условий $\sigma _{1}^{2} > 0$ и $\sigma _{2}^{2} > 0$, $0 \leqslant \lambda \leqslant 1$.

Следует отметить, что оценки, полученные методом моментов, могут служить начальными приближениями в различных численных итерационных методах при решении задачи методом максимального правдоподобия [14, 15].

4. Численный пример. Рассмотрим пример проверки гипотезы о распределении случайной величины по конкретной выборке с ${{M}_{1}}$ = 27.197, ${{M}_{2}}$ = 819.72, ${{M}_{3}}$ = 26606.499, ${{M}_{4}}$ = 911657.69, ${{M}_{5}}$ = 32498037.02. В табл. 1 приведен ее интервальный вариационный ряд.

Таблица 1

Интервалы	(7.4, 11.1)	(11.1, 14.8)	(14.8, 18.5)	(18.5, 22.2)	(22.2, 25.9)	(25.9, 29.6)
Относительные частоты	$\frac{{31}}{{1500}}$	$\frac{{99}}{{1500}}$	$\frac{{169}}{{1500}}$	$\frac{{222}}{{1500}}$	$\frac{{176}}{{1500}}$	$\frac{{130}}{{1500}}$
Интервалы	(29.6, 33.3)	(33.3, 37.0)	(37.0, 40.7)	(40.7, 44.4)	(44.4, 48.1)
Относительные частоты	$\frac{{215}}{{1500}}$	$\frac{{237}}{{1500}}$	$\frac{{142}}{{1500}}$	$\frac{{59}}{{1500}}$	$\frac{{20}}{{1500}}$

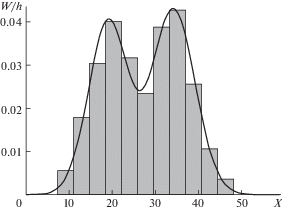
На рис. 2 приведена гистограмма относительных частот.

Рис. 2.

По виду гистограммы выдвигаем гипотезу о распределении в виде смеси двух нормальных распределений. Точечные оценки для параметров смеси находим по предложенному алгоритму в пункте 3: $\lambda = 0.46$, ${{a}_{1}} = 19.08$, ${{a}_{2}} = 34.18$, ${{\sigma }_{1}} = 4.59$, ${{\sigma }_{2}} = 4.99$. Выдвинутая гипотеза согласуется с рассмотренной выборкой по критерию согласия Пирсона c уровнем значимости 0.05. График плотности, полученной смеси приведен на рис. 2.

5. Заключение. В математической теории надежности технических систем первичными понятиями являются случайная наработка (время, расстояние) элемента (системы) до отказа и ее функция распределения. Именно они задают важнейшее понятие в теории надежности – процесс восстановления. Как указывалось во введении, известные законы распределения наработок в математической теории надежности не более чем одномодальны, что сужает возможность их применения в теории надежности технических систем.

В статье рассматриваются смеси двух и трех распределений Рэлея, Максвелла, экспоненциального и Эрланга порядка $m$, характерных для теории надежности технических систем, что дает возможность, например, получения полимодальных распределений наработок. Методом моментов получены явные формулы точечных оценок для неизвестных параметров таких смесей. Разработан численный алгоритм и приведен пример нахождения точечных оценок смеси двух нормальных распределений с использованием системы Maple.

Для простого процесса, образованного смесью n экспоненциальных распределений, предложен алгоритм получения в явном виде функции восстановления.

Рассмотренный в статье численный пример нахождения функции распределения у случайной величины по выборке с двухвершинной гистограммой показывает целесообразность дальнейшего исследования смесей классических распределений, как в задачах математической статистики, так и приложении смесей распределений в задачах теории надежности.

Конфликт интересов: Авторы заявляют, что у них нет конфликта интересов.

Список литературы

Vaynshteyn I.I. Renewal process and operation strategies in the theory of reliability of technical systems under prefailure lives distributed as a mixture of two exponential distributions / I.I. Vaynshteyn, I.M. Fedotova, G.M. Tsibul’skiy, Y.V. Vaynshteyn // Journal of Machinery Manufacture and Reliability, 2017. V. 46. № 2. P. 84–90.
Вайнштейн И.И. Процессы и стратегии восстановления с изменяющимися функциями распределения в теории надежности / И.И. Вайнштейн. Красноярск: СФУ, 2016. 189 с.
Байхельт Ф. Надежность и техническое обслуживание. Математический подход: пер. с англ. / Ф. Байхельт, П. Франкен. М.: Радио и связь, 1988. 392 с.
Айвазян С.А. Прикладная статистика. Классификация и снижение размерности / С.А. Айвазян, В.М. Бухштабер, И.С. Енюков, Л.Д. Мешалкин. М.: Финансы и статистика, 1989. 609 с.
Батракова Д.А., Королев В.Ю. Вероятностно-статистический анализ хаотических потоков в телекоммуникационных сетях с помощью скользящего разделения смесей // Системы и средства передачи информации: сб. научных трудов. М.: ИПИ РАН, 2006. С. 183–209.
Батракова Д.А., Королев В.Ю., Шоргин С.Я. Новый способ вероятностно-статистического анализа информационных потоков в телекоммуникационных сетях // Информатика и ее применение. 2007. С. 40–53.
Королев В.Ю. ЕМ-алгоритм, его модификации и их применение к задаче разделения смесей вероятностных распределений: Теоретический обзор. М.: ИПИ РАН, 2007. 94 с.
Токмачев М.С., Смирнов С.В. Программная реализация исследования смесей вероятностных распределений // Вестник Новгородского государственного университета. 2012. № 68. С. 85–89.
Барзилович Е.Ю. Вопросы математической надежности / Ю.К Беляев, В.А. Каштанов и др. М.: Радио и связь, 1983. 376 с.
Боровков А.А. Теория вероятностей. М.: Либерком, 2009. 652 с.
Гнеденко Б.В. Курс теории вероятностей / Б.В. Гнеденко. М.: Наука, 1988. 446 с.
Гнеденко Б.В. Математические методы в теории надежности: Основные характеристики надежности и их статистический анализ / Б.В. Гнеденко, Ю.К. Беляев, А.Д. Соловьев. М.: Либроком, 2013. 584 с.
Лаврентьев М.А. Методы теории функций комплексного переменного / М.А. Лаврентьев, Б.В. Шабат. М.: ЛАНЬ, 2002. 688 с.
Королев В.Ю., Назаров А.Л. Разделение смесей вероятностных распределений при помощи сеточных методов моментов и максимального правдоподобия // Автоматика и телемеханика. 2010. Выпуск 3. С. 98–116.
Горошко А.В., Ройзман В.П. Представление и обработка статистических данных, не подчиняющихся унимодальным законам распределения // Машиностроение и инженерное образование. 2013. № 3. С. 60–67.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал