Проблемы машиностроения и надежности машин, 2019, № 3, стр. 56-64

Подшипники скольжения применяются в различных машинах, содержащих вращающиеся опорные узлы. В качестве примеров можно указать компрессоры, вентиляторы, турбины, генераторы и многие другие. Конструктивные параметры подшипников и условия их эксплуатации широко варьируются в зависимости от конкретных приложений. Окружные скорости на валу могут достигать 90 м/с, а удельные нагрузки 3.5 МПа [1]. В условиях повышенных скоростей и нагрузок увеличивается температура смазочной пленки, что приводит к уменьшению вязкости и ухудшению характеристик подшипников. Например, для широко применяемого масла ISO VG32 вязкость при 40°С составляет 0.0325 Па с, а при 100°С падает до 0.0054 Па с. Между тем температуры 40–50°С часто являются температурами поступающего масла, а температуры около 100°С могут достигаться в смазочной пленке. Это делает необходимым учет зависимости вязкости от температуры при расчете подшипников.

Для повышенных условий эксплуатации [2], стандартом стало применение подшипников с самоустанавливающимися вкладышами. Подшипники и являются более дорогими и сложными по сравнению с подшипниками с фиксированной геометрией, они широко применяются, благодаря своей повышенной устойчивости. В то же время наличие подвижных вкладышей и увеличение числа степеней свободы приводит к увеличению сложности расчета подшипника. Полный расчет включает в себя решение ряда подзадач, для которых разработаны различные методы [1]. Выбор конкретных методов приводит к различным вычислительным схемам. В то же время при проектировании приходится много раз проводить расчеты для различных значений конструктивных параметров. Поэтому возникает необходимость в достаточно точной модели подшипника, имеющей умеренную вычислительную сложность. Такая модель строится в настоящей статье.

Повышенное внимание уделяется тепловым процессам, возникающим в смазочном слое. Для подшипников с самоустанавливающимися вкладышами вопрос о расчете температурного режима между вкладышами до конца не решен. В настоящей статье подробно анализируются различные схемы моделирования такого процесса.

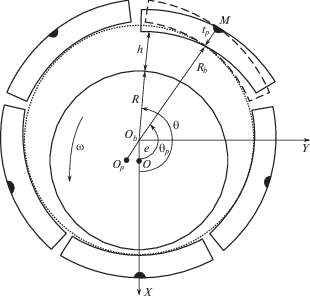
Геометрия подшипника схематически показана на рис. 1. Смазочный слой находится между поверхностями вала и вкладышей. Вал вращается с угловой скоростью ω, а вкладыши могут поворачиваться вокруг точки (или линии) закрепления (точка М), реагируя таким образом на изменения режима работы подшипника. На рис. 1 показан поворот одного из вкладышей. Обычно делается четыре или пять вкладышей. Смазка подается в смазочный слой через промежутки между вкладышами – карманы. Размеры карманов на порядок больше толщины смазочного слоя, поэтому давление в них можно считать равным давлению окружающей среды. На рис. 1 кроме того обозначены: О_b – центр подшипника, R_b – его радиус, О – центр вала, R – радиус вала, e = |О_bО| – эксцентриситет подшипника, О_p – центр кривизны вкладыша, R_p – радиус вкладыша, θ_p – угол положения точки закрепления вкладыша, t_p – толщина вкладыша.

Толщина смазочного слоя h в пределах отдельного вкладыша определяется по формуле

где ΔR_p = R_p – R – радиальный зазор вкладыша, θ_c – угол между линией центров и направлением нагрузки, m = 1 – ΔR/ΔR_p – коэффициент преднагруженности вкладыша, ΔR = R_b – R – радиальный зазор подшипника, ψ_p – угол наклона вкладыша. Величины θ_p и ψ_p имеют разные значения для каждого вкладыша, в то время как ΔR_p, m и t_p на практике обычно одинаковы.

Предположим, что на подшипник действует нагрузка, под действием которой вал и вкладыши занимают некоторое равновесное положение. Оно определяется параметрами, задающими положение центра масс вала e и θ_c и углами наклона вкладышей ψ_p (перекосы вала не учитываются). Для их вычисления решим систему уравнений статического равновесия, которая выражает равенство нулю равнодействующих сил и моментов, действующих на вал и вкладыши. Эту систему решаем методом Ньютона, на каждой итерации которого вычисляем силовые характеристики подшипника (реакцию на внешнюю нагрузку). Для вычисления силовых характеристик необходимо знать распределение давления р в смазочном слое. Его определяем из уравнения Рейнольдса, которое в случае учета зависимости вязкости от температуры имеет вид

где $U = {\omega }R$ – скорость поверхности вала, μ – динамическая вязкость смазки, которую вычисляли по формуле Фальца ${{\mu } \mathord{\left/ {\vphantom {{\mu } {{{{\mu }}_{0}}}}} \right. \kern-0em} {{{{\mu }}_{0}}}}$ = ${{\left( {{{{{T}_{0}}} \mathord{\left/ {\vphantom {{{{T}_{0}}} T}} \right. \kern-0em} T}} \right)}^{k}}$, где μ₀ – вязкость, соответствующая температуре подачи смазки T₀, Т – температура в смазочном слое, k – константа, зависящая от сорта масла. Координаты х, у, z вводятся в смазочном слое: x = Rθ – окружная координата, направленная вдоль слоя, z – осевая координата (z = 0 соответствует среднему сечению подшипника), у – координата, направленная поперек слоя, причем у = 0 соответствует границе смазка–вкладыш, а у = h границе смазка–вал. Область, занятая смазочным слоем, разбивается карманами на ряд подобластей, соответствующих вкладышам, на границах которых задавались условия равенства давления давлению окружающей среды р_а.

Однако в зависимости от условий эксплуатации в подшипнике могут возникнуть зоны кавитации. Границы таких зон определяли из условий Свифта–Штибера p(x, z) = р_а, ${{\partial p} \mathord{\left/ {\vphantom {{\partial p} {\partial x}}} \right. \kern-0em} {\partial x}}$ = 0. Уравнение (1) вместе с дополнительными условиями решали численно. Дискретизация строится методом конечных объемов, обеспечивающим на разностной сетке выполнение закона сохранения расхода, выражаемого уравнением (1). Отметим, что уравнение (1) решается в двумерной области, так как давление постоянно по толщине смазочного слоя и не зависит от у.

Учет зависимости вязкости от температуры принципиально усложняет расчет подшипника, так как уравнение Рейнольдса становится связанным через вязкость с уравнением энергии в смазке.

В отличие от давления температура меняется как вдоль слоя, так и поперек него. Для достаточно длинного подшипника температура слабо меняется в осевом направлении [3], поэтому теплопередачей в этом направлении часто пренебрегают. Принимая это предположение, полагаем, что температура является функцией только двух переменных х, у и будем определять ее в центральной плоскости z = 0. Уравнение энергии запишем в виде

где ρ – плотность смазки, с_р – теплоемкость, u, $v$ – скорости вдоль осей x и y соответственно, λ – коэффициент теплопроводности. Для вычисления скоростей используем уравнения движения смазки для тонкого слоя и уравнение неразрывности с граничными условиями u = $v$ = 0 при y = 0 и u = U при y = h. В уравнении неразрывности учтено, что в силу симметрии относительно центрального сечения ${{\partial w} \mathord{\left/ {\vphantom {{\partial w} {\partial z}}} \right. \kern-0em} {\partial z}} = 0$, где w – скорость в осевом направлении. Уравнения (3) легко решаются с учетом того, что р не зависит от у [4]. Уравнение (2) решается методом конечных разностей, при этом первые производные аппроксимируются разностями против потока.

Анализ размерностей показывает, что в уравнении (2) при члене, соответствующем теплопроводности в окружном направлении ${{\partial }^{2}}T{\text{/}}\partial {{x}^{2}}$, появляется малый коэффициент ε² (${\varepsilon } = \Delta R{\text{/}}{{R}_{b}}$), поэтому этим слагаемым пренебрегаем. Однако при больших эксцентриситетах может возникнуть обратное течение вблизи поверхности вкладыша (u < 0). В таких зонах алгоритм расчета становится неустойчивым. Здесь следует сохранить эллиптичность уравнения по обеим координатам, предупреждая возникновение вычислительной неустойчивости. Поэтому для таких областей решается полное уравнение (2), а для остальных уравнение

Область, где решается уравнение энергии, представляет собой вертикальное сечение смазочного слоя, заключенного между валом и вкладышами. Она разбивается на подобласти, определяемые границами вкладышей. Это границы вдоль поперечной координаты у, соответствующие передней и задней кромкам вкладыша, а также границы смазка–вал и смазка–вкладыш. На этих границах ставились граничные условия для уравнения (2).

На передней кромке вкладыша температура определяется температурой, с которой смазка поступает из кармана. На задней кромке, если решается уравнение (4), граничное условие не нужно. Если в пространстве между валом и вкладышем возникает обратное течение и решается уравнение (2), то ставится “мягкое” граничное условие ∂T/∂x = 0.

Для вычисления температуры во вкладышах в настоящей статье применяется подход, предложенный в [5]. При этом во вкладышах пренебрегаем теплопроводностью в окружном направлении. Учитывая, что в смазочном слое вдоль осевой координаты температура считается постоянной, то же самое принимаем и для вкладышей. Тогда уравнение теплопроводности во вкладыше становится одномерным и его можно решить аналитически. Интегрируя его при условии согласования значений температуры и тепловых потоков на границе смазка–вкладыш, получим уравнение для температуры на этой границе

где T_a – температура окружающей среды, ${\text{Nu}} = {\alpha (}{{R}_{b}} + {{t}_{p}}{)/\lambda }$ – число Нуссельта, λ_р – теплопроводность материала вкладыша, α – коэффициент теплообмена между вкладышем и окружающей средой.

Так как в положении статического равновесия вал прогревается практически равномерно, можно принять, что температура вала в установившемся состоянии будет одинаковой для всего вала. Такое предположение типично для термогидродинамического анализа подшипников [6]. Введенное предположение приводит к тому, что равенство тепловых потоков между валом и смазкой надо понимать в интегральном смысле. Тогда окончательно получим граничное условие на границе смазка–вал в виде

В зоне кавитации не существует сплошной пленки смазки, и течение представляет собой сложный двухфазный поток жидкости и газа. Обычно в этом случае используется уравнение энергии с некоторой модификацией, учитывающей тем или иным способом эффект кавитации. Одним из таких способов является так называемый метод эффективной длины [4]. Поскольку объемный расход смазки должен сохраняться, предполагаем, что масляная пленка в зоне кавитации будет сплошной, но уменьшенной протяженности. Так как градиент давления в области кавитации равен нулю, то скорость будет иметь профиль, соответствующий течению Куэтта, и эффективную длину L_eff можно рассчитать с помощью равенства объемных расходов вдоль направления скольжения ${{L}_{{{\text{eff}}}}}(x)$ = ${{h({{x}_{{{\text{cav}}}}})} \mathord{\left/ {\vphantom {{h({{x}_{{{\text{cav}}}}})} {h(x)}}} \right. \kern-0em} {h(x)}}L$, где ${{x}_{{{\text{cav}}}}}$ – окружная координата начала зоны кавитации.

Уравнение энергии решается в этой области с параметрами смазки (теплоемкость, плотность, вязкость, теплопроводность), определяемыми по формуле ${\eta }$ = ${{{\eta }}_{g}}$ + (η_f – – ${{{\eta }}_{g}}){{{{L}_{{{\text{eff}}}}}} \mathord{\left/ {\vphantom {{{{L}_{{{\text{eff}}}}}} L}} \right. \kern-0em} L}$, где η какой-либо из параметров, причем нижний индекс g относится к газу, а  f к жидкости.

Смешивание смазки между вкладышами определяет температуру, с которой масло втекает под следующий вкладыш. Поскольку в уравнении энергии в окружном направлении преобладают конвективные слагаемые, то входная температура смазки является наиболее важным граничным условием для уравнения энергии. В то же время определение температуры смазки на входе каждого вкладыша является одной из наиболее сложных проблем при анализе подшипников с самоустанавливающимися вкладышами [7].

Процесс смешивания масла в кармане обычно учитывается с помощью общего баланса тепла. При этом предполагается, что холодное (поступающее извне) и горячее (поступающее из-под вкладыша) масло полностью перемешиваются [8]. В работе [9] в модель были включены эмпирические коэффициенты, которые определяют, в какой пропорции смешивается горячее и холодное масло. Однако эти коэффициенты не являются универсальными и связаны с конкретным подшипником.

Упомянутые модели могут определить только среднюю по толщине смазочного слоя температуру масла на входе в следующий вкладыш. Однако при использовании постоянной температуры на входе во вкладыш теряется информация о градиенте температуры и, следовательно, тепловом потоке на границе смазки и вала.

В более подробных моделях предполагается, что в начале вкладыша температура имеет линейный или параболический профиль в радиальном направлении [10–12]. В случае параболического профиля для определения всех его параметров приходится привлекать дополнительные гипотезы.

Единично выполненные “точные” расчеты процесса течения в смазочном кармане последовательно указывают на то, что все смешивание происходит в тонком слое вблизи вала [13, 14].

Дж. Х. Вор [15] для расчета температуры смазки в кармане выделил контрольный объем – тонкий слой смазки, примыкающий к поверхности вала, и решая упрощенное уравнение конвективного переноса тепла рассматривал теплообмен в этом объеме. Однако при этом не моделировался отдельно процесс смешения горячей и холодной смазки.

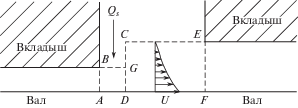
В настоящей статье также выделяется контрольный объем CDFE для течения в кармане, показанный пунктирными линиями на рис. 2. При этом надо иметь ввиду, что протяженность кармана AF на 2–3 порядка больше толщины смазочного слоя (АB или FE).

Горячая смазка выходит из-под предыдущего вкладыша (линия АВ), имея расход Q_AB, и входит в следующий (линия FE), где требуется расход Q_FE. Если Q_FE > Q_AB, то для компенсации разницы необходимо дополнительное масло Q_s с температурой T_s, которое поступает из кармана. Предполагается, что смешение происходит в объеме BADG сразу же на выходе горячего масла из-под вкладыша [15]. Похожая схема смешения для упорного подшипника была рассмотрена в работе [16]. При этом выполняется равенство тепловых потоков

Из равенства (5) можно определить среднюю температуру на линии DG. Однако при этом теряется информация о градиенте температуры и, следовательно, тепловом потоке к валу. Поэтому будем рассматривать равенство (5) локально. Для этого разобьем область BADG на полоски высотой $\Delta {{y}_{i}}$ по вертикали и запишем равенство (5) для каждой такой полоски. Фактически высота каждой полоски равняется высоте ячейки конечноразностной сетки. Таким образом вычисляется температура на линии DG (индекс полоски i для краткости записи опускаем) На остальной границе контрольного объема GCE полагаем T = T_s.

Если Q_FE < Q_AB, то дополнительное масло не требуется и в формуле (5) полагаем Q_s = 0. Это приводит к равенству тепловых потоков q_DG = q_AB или ${{u}_{{{\text{AB}}}}}{{T}_{{{\text{AB}}}}}$ = ${{u}_{{{\text{DG}}}}}{{T}_{{{\text{DG}}}}}$, откуда находим ${{T}_{{{\text{DG}}}}}$ для этого случая.

Скорости смазки в контрольном объеме определяли из уравнений для тонкого слоя (3) с учетом постоянства давления в кармане. При этом предполагали, что на границе СЕ скорость равна нулю. В частном случае, когда рассматривается модель с вязкостью, не зависящей от температуры, в продольном направлении получается профиль Куэтта, а поперечная скорость равна нулю.

В остальной части кармана температуру смазки рассчитывали путем решения в контрольном объеме уравнения энергии (4). При этом диффузионное слагаемое в угловом направлении не учитывали ввиду отсутствия здесь обратных течений.

После определения температурного поля в смазочном слое всего подшипника рассчитываются новые значения величины вязкости, вновь решается уравнение Рейнольдса, уравнение энергии и весь процесс повторяется до достижения заданной точности при определении параметров равновесного положения.

Для верификации модели проводили сравнение с экспериментальными данными работы [17] для подшипника с четырьмя самоустанавливающимися вкладышами. Во всех экспериментах внешняя нагрузка была приложена между вкладышами. Параметры подшипника приведены в табл. 1.

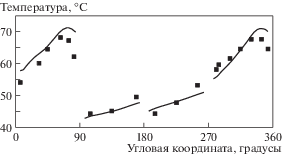
На рис. 3 представлено распределение температуры на поверхностях вкладышей. Сплошные линии – расчет, черные квадраты – эксперимент (аналогично и на рис. 4). В целом можно заключить, что имеет место удовлетворительное согласование расчетных и экспериментальных данных. Как и ожидалось, два вкладыша, между которыми направлена нагрузка, имеют значительно большую температуру, чем остальные. Это связано с тем, что в данной области зазор минимален.

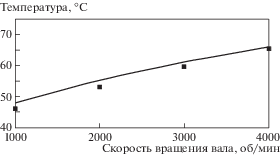
Большой интерес представляет температура вала, так как чрезмерный нагрев поверхности вала может приводить к термической неустойчивости (эффект Мортона) [18]. На рис. 4 представлена зависимость температуры вала от скорости его вращения. Из рис. 4 видно, что температура вала возрастает с увеличением скорости вращения, хорошо согласуясь с экспериментальными данными. Отличие между рассчитанными значениями и экспериментальными не превышает 3%.

В заключение отметим, что в статье построена термогидродинамическая модель подшипника с самоустанавливающимися вкладышами, состоящая из ряда подмоделей. Для определения давления в смазочном слое использовали уравнение Рейнольдса в форме, учитывающей зависимость вязкости от температуры. Возможную кавитацию учитывали методом эквивалентной длины. Для определения температуры использовали уравнение энергии в предположении постоянства температуры в осевом направлении. Для описания процесса смешения с поступающим извне маслом в пространстве между вкладышами была построена модель, основанная на использовании уравнения энергии в тонком слое.

Сравнение результатов расчета с экспериментальными данными позволяет заключить, что предложенная термогидродинамическая модель достаточно хорошо описывает процессы в смазочном слое подшипника с самоустанавливающимися вкладышами и может служить основой для проектирования таких подшипников.

Конфликт интересов: Авторы заявляют, что у них нет конфликта интересов.