Проблемы машиностроения и надежности машин, 2019, № 3, стр. 27-35
НЕЛИНЕЙНЫЙ ИЗГИБ ПОЛОГОЙ ПАНЕЛИ ПОД ДЕЙСТВИЕМ ДАВЛЕНИЯ ГАЗА
М. А. Ильгамов 1, 2, *, В. Е. Моисеева 2, **
1 Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия
2 Институт механики и машиностроения ФИЦ “Казанский научный центр РАН”
Казань, Россия
* E-mail: ilgamov@anrb.ru
** E-mail: vemoi@yandex.ru
Поступила в редакцию 13.09.2018
Принята к публикации 18.02.2019
Аннотация
Рассмотрен изгиб круглой весьма пологой панели под действием избыточных давлений на нижнюю и верхнюю поверхности. Используется уточненное выражение распределенной поперечной силы, зависящей не только от перепада давлений на поверхности, но и от взаимодействия среднего избыточного давления и кривизны срединной поверхности. Это уточнение проводится в линейном приближении. Предполагается, что кромка панели изолирована от избыточного давления. Дополнена классическая теория нелинейного изгиба круглой пологой панели под действием давлений на ее поверхности.
Введение. Отличительной чертой весьма пологой панели или пластины с начальной погибью является реализация разных напряженно-деформированных состояний в зависимости от знака перепада давлений на ее поверхности [1, 2]. Если обозначить через h толщину, γ – удельный вес материала, $\gamma h$ – вес единичной площадки панели, ${{p}_{1}}$, ${{p}_{2}}$ – избыточные давления, действующие на нижнюю и верхнюю поверхности панели выпуклостью вниз, то при увеличении поперечной нагрузки, направленной вниз (${{p}_{1}} < \gamma h + {{p}_{2}}$), происходит плавное возрастание ее прогиба. При ${{p}_{1}} > \gamma h + {{p}_{2}}$ и некоторых дополнительных условиях на входные параметры может происходить резкое перемещение панели в сторону ее вогнутости (“хлопок” [2]). Подъемистые панели прохлопывают, как правило, по несимметричной форме. Для весьма пологих панелей характерна только симметричная форма прохлопывания [2–6].
Насколько известно, в литературе [1–10] отсутствует анализ напряженно-деформированного состояния при изгибе тонких упругих пластин, оболочек и мембран в зависимости от среднего давления окружающей среды. В классической теории изгиба принимается, что поперечная распределенная нагрузка q на тонкую пластину равна $q = \gamma h + {{p}_{2}} - {{p}_{1}}$. В случае малого среднего избыточного давления или приложения избыточного давления только к одной из поверхностей, а также малом отношении среднего давления к модулю упругости материала Е это значение q является достаточно точным.
Учет влияния разности площадей нижней и верхней поверхностей, среднего давления pm = (p1 + p2)/2 на цилиндрический изгиб удлиненной пластины приводит к выражению для распределенной поперечной нагрузки [11, 12]
где функция прогиба w(x) зависит от эффективной жесткости D(1 + α). Здесь D – изгибная жесткость пластины, α – безразмерный параметр, который для шарнирно закрепленной пластины длиной L равен При получении (1), (2) предполагается, что кромки пластины изолированы от действия давлений р1, р2. Это зависит от конструкции опорных устройств (например, защемление, которое препятствует продольному перемещению пластины).Для конструкций типа железобетонных, корабельных при атмосферном давлении или односторонних невысоких давлениях параметр α равен нулю или весьма мал. Но для конструкций оборудования нефтехимии, энергетики, глубоководных аппаратов, аэрокосмической техники могут быть немалые значения α. Если $E = 2 \times {{10}^{6}}$ бар (сталь), ${{p}_{m}} = 20$ бар, $L{\text{/}}h = {{10}^{2}}$, то $\alpha = 0.1$. Эффективная жесткость повышается на 10%. В случае $E = 2 \times {{10}^{5}}$ бар (магниевый сплав) параметр α = 1. При этом эффективная жесткость равна 2D, прогиб меньше в два раза, чем в случае, когда не учитывается разность площадей верхней и нижней поверхностей пластины.
В работе [12] значение прогиба при определении параметра α по моделям Кирхгоффа и Тимошенко сравнивается с классическим результатом. В [13] изучено поведение пластины при вакуумировании ее поверхностей. При этом значение параметра α отрицательное. Установлена возможность выпучивания пластины под действием среднего отрицательного давления при равенстве отрицательных избыточных давлений.
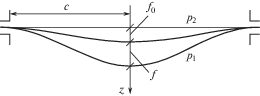
1. Постановка задачи. Круглая весьма пологая панель, выпуклостью обращенная вниз, испытывает давления p0 + p1, p0 + p2 на нижнюю и верхнюю поверхности (рис. 1). Здесь p0 – атмосферное давление, p1, p2 − избыточные давления, которые могут иметь и отрицательные значения (вакуумирование поверхностей панели). В последнем случае должно быть ограничение p0 + p1 ≥ 0, p0 + p2 ≥ 0. Для случая жидкости можно принять p0 + p1 ≥ ${{p}_{\text{v}}}$, p0 + p2 ≥ ${{p}_{\text{v}}}$, где ${{p}_{\text{v}}}$ – давление насыщенных паров (для воды ${{p}_{\text{v}}}$ = = 0.022 бар). Задаются определенные условия закрепления на кромке r = с и действия давления на эти кромки. Предполагается, что на сечение r = с действует либо только давление p0, либо p0 + pm, где pm − среднее избыточное давление. Под действием этих давлений и собственного веса происходит осесимметричный изгиб. Направление вниз принимается за положительные значения распределенной поперечной силы q, начального и текущего прогибов, оси z.
Система нелинейных уравнений весьма пологой панели (или пластины с начальной погибью ${{w}_{0}}(r)$) относительно функции прогиба $w(r)$ и функции напряжений $\Phi (r)$ имеет вид [2, c. 179]
(3)
$\begin{gathered} D\frac{d}{{dr}}({{\nabla }^{2}}w) - \frac{h}{r}\frac{{d\Phi }}{{dr}}\left( {\frac{{d{{w}_{0}}}}{{dr}} + \frac{{dw}}{{dr}}} \right) = \Psi ,{\text{ }} \\ \frac{d}{{dr}}({{\nabla }^{2}}\Phi ) + \frac{E}{r}\left[ {\frac{{d{{w}_{0}}}}{{dr}}\frac{{dw}}{{dr}} + \frac{1}{2}{{{\left( {\frac{{dw}}{{dr}}} \right)}}^{2}}} \right] = 0, \\ D = \frac{{E{{h}^{3}}}}{{12(1 - {{\nu }^{2}})}},\quad {{\sigma }_{r}} = \frac{{d\Phi }}{{rdr}},\quad {{\sigma }_{\varphi }} = \frac{{{{d}^{2}}\Phi }}{{d{{r}^{2}}}},\quad \Psi = \frac{1}{r}\int\limits_0^r {qrdr} . \\ \end{gathered} $Предполагается, что в начальном состоянии панель находится под всесторонним атмосферным давлением p0 (оно действует также на кромку r = с). Это состояние панели считается ненапряженным. Прогиб w возникает при действии избыточных давлений p1 и p2. Относительно w, Φ используются граничные условия защемления и свободного перемещения точек контура по радиусу
Нелинейная краевая задача (3)–(4) основана на гипотезах Кирхгоффа [2]. При определении поперечной распределенной нагрузки $q$ также остаемся в рамках этих гипотез, в соответствии с которыми кривизны срединной поверхности равны(5)
${{\kappa }_{r}} = - \frac{{{{d}^{2}}({{w}_{0}} + w)}}{{d{{r}^{2}}}},\quad {{\kappa }_{\varphi }} = - \frac{{d({{w}_{0}} + w)}}{{rdr}}.$(6)
$\begin{gathered} d{{S}_{1}} = dr\left( {1 + \frac{h}{2}{{\kappa }_{r}}} \right)rd\varphi \left( {1 + \frac{h}{2}{{\kappa }_{\varphi }}} \right), \\ d{{S}_{2}} = dr\left( {1 - \frac{h}{2}{{\kappa }_{r}}} \right)rd\varphi \left( {1 - \frac{h}{2}{{\kappa }_{\varphi }}} \right). \\ \end{gathered} $Равнодействующая поперечных сил равна
Здесь собственный вес панели отнесен к срединной поверхности. Подставляя выражения (5), (6) в (7) и отбрасывая нелинейные члены, получаем(8)
$\begin{gathered} q = {{p}_{e}} + {{p}_{m}}h{{\nabla }^{2}}({{w}_{0}} + w),\quad {{p}_{e}} = \gamma h + {{p}_{2}} - {{p}_{1}}, \\ {{\nabla }^{2}} = \frac{d}{{rdr}}\left( {r\frac{d}{{dr}}} \right),\quad {{p}_{m}} = \frac{{{{p}_{1}} + {{p}_{2}}}}{2}. \\ \end{gathered} $С учетом $q$ из (8) функцию $\Psi $ можно записать в виде
(9)
$\Psi = \frac{{{{p}_{e}}r}}{2} + \frac{{{{p}_{m}}h}}{r}\int\limits_0^r {r{{\nabla }^{2}}(w + {{w}_{0}})dr = } \frac{{{{p}_{e}}r}}{2} + {{p}_{m}}h\frac{d}{{dr}}(w + {{w}_{0}}).$С целью упрощения анализа принимаем приближенные выражения для начальных и дополнительных прогибов, удовлетворяющие условиям (4), в виде [2, с. 205]
(10)
${{w}_{0}} = {{f}_{0}}{{(1 - {{r}^{2}}{\text{/}}{{c}^{2}})}^{2}},\quad w = f{{(1 - {{r}^{2}}{\text{/}}{{c}^{2}})}^{2}}.$Подставив функции (10) во второе уравнение (3), получаем следующее ограниченное при $r = 0$ выражение
(11)
$\frac{{d\Phi }}{{dr}} = - \frac{{E({{f}^{2}} + 2f{{f}_{0}})}}{{6c}}\left( {6\frac{{{{r}^{3}}}}{{{{c}^{3}}}} - 4\frac{{{{r}^{5}}}}{{{{c}^{5}}}} + \frac{{{{r}^{7}}}}{{{{c}^{7}}}}} \right) + \frac{{Cr}}{2}.$(12)
$\begin{gathered} A({{\xi }^{3}} + 3{{\xi }_{0}}{{\xi }^{2}} + 2\xi _{0}^{2}\xi ) + \frac{{16}}{{3(1 - {{\nu }^{2}})}}[(1 + \alpha )\xi + \alpha {{\xi }_{0}}] = q*, \\ A = \frac{6}{7},\quad {{\xi }_{0}} = \frac{{{{f}_{0}}}}{h},\quad q* = \left( {\frac{{{{p}_{e}}}}{E}} \right){{\left( {\frac{c}{h}} \right)}^{4}},\quad \alpha = \kappa \left( {\frac{{{{p}_{m}}}}{E}} \right){{\left( {\frac{c}{h}} \right)}^{2}},\quad \kappa = \frac{{3(1 - {{\nu }^{2}})}}{4}. \\ \end{gathered} $Известно [4], что при условии соответствия аппроксимаций дополнительного прогиба пластинки и ее начальной погиби, вывод основного уравнения можно распространить и на другие граничные условия. Например, при условиях шарнирного опирания, когда точки контура смещаются свободно
(13)
$w = 0,\quad \frac{{{{d}^{2}}w}}{{d{{r}^{2}}}} + \frac{\nu }{r}\frac{{dw}}{{dr}} = 0,\quad \frac{{d\Phi }}{{rdr}} = 0\quad (r = c),$2. Изгиб при направлении нагрузки в сторону выпуклости панели. В этом случае γh + p2 > > ${{p}_{1}}$ (${{p}_{e}} < 0$). Рассмотрим случай защемления кромки панели.
На рис. 2 изображены монотонно возрастающие зависимости $q{\text{*}}(\xi )$ по (12) при $\alpha = 6$ (сплошные линии) и $\alpha = 0$ (штриховые линии) для ряда значений начальной погиби ξ0. С увеличением поперечной силы происходит рост относительного дополнительного прогиба ξ, что увеличивает кривизну панели.
Рис. 2.
Зависимость безразмерной стрелы прогиба ξ от безразмерной распределенной поперечной силы $q{\text{*}}$, направленной в сторону выпуклости круглой панели разной пологости (${{\xi }_{0}}$ = 0; 1; 2), при параметрах α = 0 (штриховые линии) и α = 6 (сплошные линии).
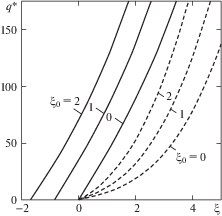
В классическом решении [2] рост прогиба начинается, как только появляется поперечная сила $q{\text{*}}$ (штриховые линии на рис. 2). В отличие от него при $\alpha > 0$ положительный прогиб проявляется только при некотором ненулевом значении поперечной силы $q{\text{*}}$. Чем больше параметр α, тем больше значение $q{\text{*}}$, при котором начинается дополнительный прогиб панели. Это значение $q{\text{*}}$ может быть определено из уравнения (12), в котором отбрасываются нелинейные члены. Решение его имеет вид
(14)
$\left( {\frac{{12}}{7}\xi _{0}^{2} + \frac{{16(1 + \alpha )}}{{3(1 - {{\nu }^{2}})}}} \right)\xi = q{\text{*}} - \frac{{16\alpha {{\xi }_{0}}}}{{3(1 - {{\nu }^{2}})}}.$(15)
$\frac{{{{p}_{e}}}}{{{{p}_{m}}}} > 4\left( {\frac{{{{f}_{0}}}}{h}} \right){{\left( {\frac{h}{c}} \right)}^{2}}.$(16)
$\varepsilon \approx \frac{{7{{\xi }_{0}}}}{{7(1 + \alpha ) - \xi _{0}^{2}}},\quad \xi \approx - \frac{{(7\alpha - {{\xi }_{0}}){{\xi }_{0}}}}{{7(1 + \alpha ) - \xi _{0}^{2}}}.$Для значений параметра α с разными знаками на рис. 3 представлены зависимости безразмерного прогиба в центре панели от безразмерного параметра $q{\text{*}}$ для значений ${{\xi }_{0}} = 0$; 1; 2. Видно, что в окрестности $q{\text{*}} = 0$, при ${{\xi }_{0}} > 0$, $\alpha = 0.3$ за счет влияния среднего давления pm наблюдается изгиб в сторону вогнутости (при нарушении условия (15)), затем прогиб плавно возрастает. Как и выше, при фиксированном значении $q{\text{*}}$ при увеличении α прогиб в центре уменьшается, а при отрицательном значении α – возрастает.
Рис. 3.
Зависимость безразмерной стрелы прогиба ξ от безразмерной распределенной поперечной силы $q{\text{*}}$, направленной в сторону выпуклости круглой панели при разных значениях пологости (${{\xi }_{0}}$ = 0; 1; 2) и параметра α (0; 0.3; –0.3).
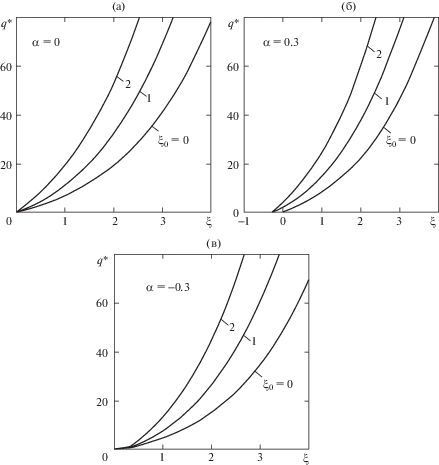
Линейное решение (14) неограниченно возрастает при значении параметра $\alpha \approx - 1$ – – $0.3\xi _{0}^{2}$ (при $\nu $ = 1/3), которое можно считать критическим. Для вакуумированной плоской пластины (${{\xi }_{0}} = 0$) критическое значение равно $\alpha = - 1$ [13]. При этом предполагается, что на кромки пластины и панели действует только давление ${{p}_{0}}$.
3. Изгиб при поперечном направлении нагрузки в сторону вогнутости панели. При этом нужно изменить знак в правой части уравнения (12) или знак ξ0 на отрицательный (рис. 4a). Примем последний случай. Тогда уравнение (12) приобретает вид
(17)
$A({{\xi }^{3}} - 3{{\xi }_{0}}{{\xi }^{2}} + 2\xi _{0}^{2}\xi ) + \frac{{16}}{{3(1 - {{\nu }^{2}})}}((1 + \alpha )\xi - \alpha {{\xi }_{0}}) = q{\text{*}}.$(18)
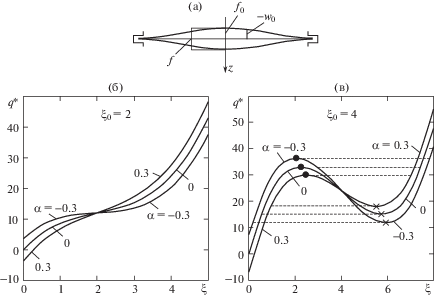
$\begin{gathered} 3A{{\xi }^{2}} - 6A{{\xi }_{0}}\xi + 2A\xi _{0}^{2} + \frac{{16}}{{3(1 - {{\nu }^{2}})}}(1 + \alpha ) = 0, \\ \left| {{{\xi }_{0}}} \right| \geqslant \frac{4}{3}\sqrt {\frac{{3(1 + \alpha )}}{{A(1 - {{\nu }^{2}})}}} ,\quad \xi = {{\xi }_{0}} \pm \sqrt {\frac{{\xi _{0}^{2}}}{3} - \frac{{16(1 + \alpha )}}{{9A(1 - {{\nu }^{2}})}}} . \\ \end{gathered} $Рис. 4.
Зависимость безразмерной стрелы прогиба ξ круглой панели от безразмерной поперечной силы $q{\text{*}}$, направленной в сторону вогнутости при разных значениях пологости (${{\xi }_{0}}$ = 2; 4) и параметра α (0; 0.3; –0.3).
При этом верхняя и нижняя критические силы равны
При малой относительной начальной погиби (рис. 4б) с ростом перепада давления прогиб монотонно возрастает. Увеличение параметра $\alpha $ при фиксированном значении $q{\text{*}}$ до точки перегиба (${{d}^{2}}q{\text{*/}}d{{\xi }^{2}}$ = 0) при $\xi = {{\xi }_{0}}$ приводит к росту прогиба, а после – к уменьшению. Это объясняется тем, что до положения панели, совпадающей с плоскостью, проходящей через круговую опору (до точки перегиба), направления сил от перепада давлений и среднего давления совпадают. После перехода через плоскость, сила от среднего давления направлена против силы от перепада ввиду изменения знака кривизны. Это видно по соотношениям (8).
При выполнении условия (18) (${{\xi }_{0}} = 4$, рис. 4в) после достижения верхней критической силы с интенсивностью $q_{B}^{*}$, отмеченной точками, происходит хлопок. Хлопок представляет собой скачкообразный переход панели из равновесного состояния с относительно небольшими прогибами в равновесное состояние с большими прогибами [2, 7]. При последовательном уменьшении силы после достижения $q_{H}^{{\text{*}}}$ (значок ×) панель скачком возвращается в состояние с малыми прогибами. Из рис. 4в видно, что наибольшие значения верхней критической силы $q_{B}^{*}$ наблюдаются при вакуумировании ($\alpha = - 0.3$), увеличение параметра $\alpha $ приводит к уменьшению $q_{B}^{*}$. До хлопка при постоянном значении перепада давления с ростом $\alpha $ прогиб увеличивается. После хлопка при фиксированном значении $q{\text{*}}$ с увеличением параметра $\alpha $ прогиб уменьшается. Отметим, что в данном примере наименьшие значения $q_{H}^{*}$ наблюдаются при $\alpha = - 0.3$.
5. Заключение. Влияние на изгиб среднего избыточного давления pm = (p1 + p2)/2 на поверхности тонкой круглой весьма пологой панели радиусом с и толщиной h определяется безразмерным параметром $\alpha \approx \kappa \left( {\frac{{{{p}_{m}}}}{E}} \right){{\left( {\frac{c}{h}} \right)}^{2}}$, где Е – модуль упругости материала, κ – коэффициент, зависящий от граничных условий (при $\nu $ = 1/3 для шарнирного опирания κ = 0.99, при защемлении – κ = 0.67), p1, p2 – избыточные давления на нижнюю и верхнюю поверхности.
В случае, когда распределенная поперечная нагрузка q = γh + p2 – p1 направлена в сторону выпуклости панели, происходит монотонное возрастание ее прогиба. Но при увеличении параметра $\alpha $ для фиксированного значения q прогиб уменьшается. При высоких значениях $\alpha $, когда влияние среднего давления превосходит поперечную силу, панель выпрямляется, принимает плоскую форму.
Если поперечная нагрузка действует на панель в направлении начальной вогнутости, то при больших ξ0 достигаются верхняя и нижняя критические нагрузки. При этом наибольшее и наименьшее значения критической нагрузки наблюдаются при отрицательных значениях параметра $\alpha $.
Благодарности. Авторы выражают благодарность М.С. Ганеевой и З.В. Скворцовой за обсуждение статьи.
Конфликт интересов: Авторы заявляют, что у них нет конфликта интересов.
Список литературы
Timoshenko S. Theory of Plates and Shells. New York: McGraw–Hill Book Company Inc., 1940. 399 р. (Тимошенко С.П. Пластины и оболочки. М.; Л.: Гостехиздат, 1948. 460 с.)
Вольмир А.С. Гибкие пластинки и оболочки. М.: Гостехиздат, 1956. 420 с.
Феодосьев В.И. К расчету хлопающей мембраны // ПММ. 1946. Т. 10. № 2. С. 295–300.
Nylander H. Die Durchschlaglast von Platten // Oesterr. Ing.-Archiv. 1955. № 2–3. P. 181–196.
Муштари Х.М., Галимов К.З. Нелинейная теория упругих оболочек. Казань: Таткнигоиздат, 1957. 431 с.
Корнишин М.С. Нелинейные задачи теории пластин и пологих оболочек и методы их решения. М.: Наука, 1964. 191 с.
Корнишин М.С., Исанбаева Ф.С. Гибкие пластины и панели. М.: Наука, 1968. 260 с.
Свирский И.В. Методы типа Бубнова–Галеркина и последовательных приближений. М.: Наука, 1968. 200 с.
Ворович И.И. Математические проблемы нелинейной теории пологих оболочек. М.: Наука, 1989. 376 с.
Shen H.Sh. Postbuckling Behavior of Plates and Shells. Shanghai Jiao Tong University, 2017. 675 p.
Ильгамов М.А. Влияние давления окружающей среды на изгиб тонкой пластины и пленки // ДАН. 2017. Т. 476. № 4. С. 402–405.
Ильгамов М.А. О влиянии давления окружающей среды на изгиб пластины // Проблемы машиностроения и надежности машин. 2017. № 5. С. 30–35.
Ильгамов М.А. Изгиб и устойчивость тонкой пластины при вакуумировании ее поверхностей // ДАН. 2018. Т. 480. № 5. С. 542–544.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин