1. На главную
  2. Электронные версии
  3. Проблемы машиностроения и надежности машин
  4. № 4, 2019

Проблемы машиностроения и надежности машин, 2019, № 4, стр. 14-21

СТРУКТУРНЫЙ И КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА ДЛЯ ОБРАБОТКИ ВНУТРЕННИХ ПОВЕРХНОСТЕЙ

А. С. Фомин 1, *, М. Е. Парамонов 1

1 Сибирский государственный индустриальный университет
Новокузнецк, Россия

* E-mail: alexey-nvkz@mail.ru

Поступила в редакцию 12.03.2018
Принята к публикации 24.04.2019

Полный текст (PDF)

Аннотация

Настоящее исследование посвящено структурному и кинематическому анализу, а также разработке трехмерной параметрической модели механизма для обработки внутренних поверхностей. Движение выходного элемента исследуемого механизма в пространстве ограничивается двумя общими наложенными связями. Механизм позволяет варьировать траекторию движения выходного звена за счет изменения длины неподвижного звена (стойки). Применение данного механизма кроме обработки внутренних поверхностей может быть реализовано в устройствах для перемешивания различных смесей, лазерной резки и воспроизведения пространственных кривых.

Ключевые слова: механизм, кинематическая пара, наложенная связь, степень свободы

1. Введение. Одной из ведущих отраслей промышленного развития ряда государств является машиностроение. Развитие данной отрасли неразрывно связано с постоянным внедрением новейших высокоэффективых механических систем, позволяющих решать актуальные технологические задачи, поставленные практикой. Механические системы, имеющие возможность функционирования с минимальным числом звеньев, реализующие пространственные движения выходных элементов и организованные исключительно из одноподвижных кинематических пар, имеют ряд преимуществ, к которым относится долговечность их конструкций, возможность получения высоких скоростей звеньев, повышенный КПД, точность, надежность и другие важные технологические свойства.

Такие механические системы имеют как параллельную [1, 2], так и последовательную структуру [3], и создаются с разным числом общих наложенных связей, лежащим в диапазоне от нуля до четырех [4]. Системы без наложенных связей относятся к классически пространственным, в них выходные звенья имеют шесть степеней свободы и могут беспрепятственно поворачиваться и смещаться относительно каждой из осей координат [5]. Механизмы с одной и двумя общими наложенными связями также являются пространственными, однако относительно некоторых из осей координат движения звеньев в них являются запрещенными [3, 6–8]. Три общих наложенных связи описывают структуру плоских и сферических механизмов [9, 10], а четыре – винтовых и клиновых [11].

Настоящая статья посвящена исследованию пространственного механизма, в котором движение выходного звена ограничивается двумя общими наложенными связями. Вместе с тем, в исследуемом механизме реализована возможность изменения траектории движения выходного звена за счет изменения длины стойки. Данный тип механизмов является одним из простейших пространственных по числу звеньев и имеет меньшее число избыточных связей по сравнению с плоскими, сферическими и клиновыми механизмами. Несмотря на очевидные конструктивные преимущества механизмов данного типа, результаты их исследования представлены в настоящее время не в полной мере, что можно объяснить отсутствием детализированных методов их синтеза и анализа. В связи с этим целью настоящего исследования является проведение структурного и кинематического анализа механизма с двумя общими наложенными связями, применение которого целесообразно при обработке внутренних поверхностей деталей машин.

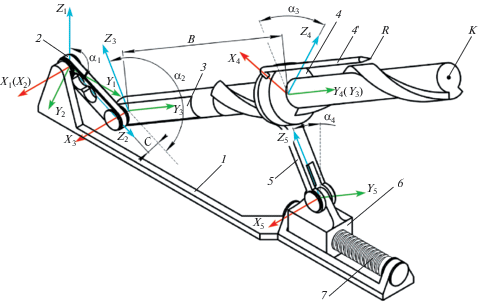
2. Структурный анализ механизма. Обратимся к анализу структуры исследуемого механизма, кинематическая схема которого показана на рис. 1 [12]. Механизм включает в свой состав стойку 1, кривошип 2, винтовой шатун 3, гайку 4 с обрабатывающим элементом 4 ', коромысло 5, ползун 6 и винт 7. Все звенья входят между собой в кинематические пары только пятого класса. Пары звеньев 1–2, 2–3, 4–5, 5–6 и 7–1 выполнены вращательными, причем геометрические оси пар 1–2, 2–3 и 5–6 параллельны друг другу и лежат в перпендикулярной плоскости к осям пар звеньев 4–5 и 7–1. Кинематические пары звеньев 3–4 и 6–7 выполнены винтовыми. Пара звеньев 6–1 выполнена поступательной. Звенья 1–5 образуют винто-рычажный механизм, подвижность которого определяется по формуле для кинематических цепей с двумя общими наложенными связями и равна одному (W2 = 1) [6]. Звенья 1, 6 и 7 образуют винтовой механизм, подвижность которого вычисляется по формуле для кинематических цепей с четырьмя общими наложенными связями и также равна одному (W4 = 1) [11]. Таким образом, общая подвижность механизма для обработки внутренних поверхностей определяется путем сложения подвижностей обеих кинематических цепей, входящих в его состав, и равна двум (W2, 4 = 1). Это означает, что движение в механизме задается двум звеньям кривошипу 2 и винту 7. Однако движение винта 7 требуется для изменения длины стойки 1, т.е. установки коромысла 5 на заданном расстоянии от шарнира 1–2. Это позволяет изменить траекторию движения элемента 4 ', жестко установленного на гайке 4. Также может быть изменена длина кривошипа 2 посредством смещения кинематической пары звеньев 1–2 вдоль кривошипа 2 за счет выполненных на нем отверстий (рис. 1). Таким образом, с учетом изменяемых параметров могут быть получены разные траектории движения выходного звена, гайки 4 с элементом 4 '.

Рис. 1.

Кинематическая схема механизма для обработки внутренних поверхностей.

3. Кинематический анализ механизма. Обратимся к определению положения точки R элемента 4' в пространстве (рис. 1). Механизм приводится в движение вращением кривошипа 2 вокруг оси х1 на угол α1. Для исследования кинематики данного механизма применим аналитический метод преобразования координат, который широко используется при изучении пространственных кинематических цепей и манипуляторов [13, 14].

С каждым из звеньев механизма свяжем прямоугольную систему координат. Начало системы координат O1x1y1z1 связано со стойкой 1, начало системы координат O2x2y2z2 связано с кривошипом 2. Центры обеих систем координат совпадают и расположены во вращательной кинематической паре звеньев 1–2 так, что оси x1 и x2 совпадают. Положение системы координат O2x2y2z2 в системе O1x1y1z1 определяется матрицей Денавита–Хартенберга

${{T}^{{\left( {2,1} \right)}}} = \left( {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&{\cos ({{\alpha }_{1}})}&{\sin ({{\alpha }_{1}})} \\ 0&0&{ - \sin ({{\alpha }_{1}})}&{\cos ({{\alpha }_{1}})} \end{array}} \right).$

Начало системы координат O3x3y3z3 связано с шатуном 3 и расположено в кинематической паре звеньев 2–3. Оси координат x2 и x3 параллельны друг другу. Положение системы координат O3x3y3z3 в системе O2x2y2z2 определится матрицей Денавита–Хартенберга следующего вида

${{T}^{{\left( {3,2} \right)}}} = \left( {\begin{array}{*{20}{c}} 1&0&0&0 \\ { - c}&1&0&0 \\ 0&0&{\cos ({{\alpha }_{2}})}&{ - \sin ({{\alpha }_{2}})} \\ {{{l}_{2}}}&0&{\sin ({{\alpha }_{2}})}&{\cos ({{\alpha }_{2}})} \end{array}} \right),$
где c – заданный конструктивный размер; l2 – заданная длина кривошипа 2; α2 – неизвестная переменная, характеризующая поворот шатуна 3 относительно кривошипа 2. Параметры с и l2 определяют смещение системы координат O3x3y3z3 относительно O2x2y2z2.

Начало системы координат O4x4y4z4 связано с гайкой 4 и расположено в кинематической паре звеньев 3–4, причем оси у3 и у4 совпадают. Положение системы координат O4x4y4z4 в системе O3x3y3z3 определяется матрицей Денавита–Хартенберга, записанной в виде

${{T}^{{\left( {4,3} \right)}}} = \left( {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&{\cos ({{\alpha }_{3}})}&0&{ - \sin ({{\alpha }_{3}})} \\ B&0&1&0 \\ 0&{\sin ({{\alpha }_{3}})}&0&{\cos ({{\alpha }_{3}})} \end{array}} \right),$
где B – переменный размер, характеризующий смещение гайки 4 относительно винтового шатуна 3; α3 – неизвестная переменная, характеризующая поворот гайки 4 относительно винтового шатуна 3.

Начало системы координат O5x5y5z5 связано с коромыслом 5 и расположено в кинематической паре звеньев 5–1. Положение системы координат O5x5y5z5 в системе O4x4y4z4 определяется матрицей Денавита–Хартенберга

${{T}^{{\left( {5,4} \right)}}} = \left( {\begin{array}{*{20}{c}} 1&0&0&0 \\ { - {{l}_{5}}\sin ({{\alpha }_{3}})}&{\cos ({{\alpha }_{3}})}&0&{\sin ({{\alpha }_{3}})} \\ 0&0&1&0 \\ { - {{l}_{5}}\cos ({{\alpha }_{3}})}&{ - \sin ({{\alpha }_{3}})}&0&{\cos ({{\alpha }_{3}})} \end{array}} \right),$
где l5 – заданная длина коромысла 5, определяющая смещение начала системы координат O5x5y5z5 относительно O4x4y4z4.

Положение системы координат O1x1y1z1 в системе O5x5y5z5 определяется матрицей Денавита–Хартенберга

${{T}^{{\left( {1,5} \right)}}} = \left( {\begin{array}{*{20}{c}} 1&0&0&0 \\ c&1&0&0 \\ { - {{l}_{1}}\cos ({{\alpha }_{4}})}&0&{\cos ({{\alpha }_{4}})}&{\sin ({{\alpha }_{4}})} \\ { - {{l}_{1}}\sin ({{\alpha }_{4}})}&0&{ - \sin ({{\alpha }_{4}})}&{\cos ({{\alpha }_{4}})} \end{array}} \right),$
где α4 – неизвестная переменная, характеризующая поворот коромысла 5 относительно стойки 1; l1 – заданная длина стойки 1, определяющая расстояние между центрами систем координат O1x1y1z1 и O5x5y5z5.

Уравнение замкнутости контура исследуемого механизма запишется в следующем виде

(1)
${{T}^{{\left( {2,1} \right)}}}{{T}^{{\left( {3,2} \right)}}}{{T}^{{\left( {4,3} \right)}}}{{T}^{{\left( {5,4} \right)}}}{{T}^{{\left( {1,5} \right)}}} = E,$
где Е – единичная матрица.

Положение точки R элемента 4 ' в системе координат O1x1y1z1 определится из следующего выражения

$\left( {\begin{array}{*{20}{c}} 1 \\ {{{x}_{{1R}}}} \\ {{{y}_{{1R}}}} \\ {{{z}_{{1R}}}} \end{array}} \right) = {{T}^{{\left( {2,1} \right)}}}{{T}^{{\left( {3,2} \right)}}}{{T}^{{\left( {4,3} \right)}}}\left( {\begin{array}{*{20}{c}} 1 \\ m \\ n \\ 0 \end{array}} \right),$
где x1R, y1R, z1R – координаты точки R в системе O1x1y1z1, m и n – заданные параметры, определяющие длину элемента 4' по осям x4 и y4. Переменные значения углов α2, α3, α4 и смещение В определяются из выражения (1).

Положение точки K, принадлежащей винтовому шатуну 3 (рис. 1) и перемещающейся в плоскости, в системе O1x1y1z1 определится, как

$\left( {\begin{array}{*{20}{c}} 1 \\ {{{x}_{{1K}}}} \\ {{{y}_{{1K}}}} \\ {{{z}_{{1K}}}} \end{array}} \right) = {{T}^{{\left( {2,1} \right)}}}{{T}^{{\left( {3,2} \right)}}}\left( {\begin{array}{*{20}{c}} 1 \\ 0 \\ {{{l}_{3}}} \\ 0 \end{array}} \right),$
где x1K, y1K, z1K – координаты точки K в системе O1x1y1z1, l3 – заданная длина винтового шатуна 3.

Далее задача решается численными методами. Были заданы следующие параметры: l1 = 186 мм, l2 = 40 мм, l3 = 290 мм, l5 = 62 мм, с = 9.5 мм, m = 23 мм, n =100 мм, шаг резьбы p = 85 мм. По результатам проведенных расчетов сформированы табл. 1 и 2, где приведены численные значения всех переменных параметров (α2, α3, α4, B, xR, yR, zR, yK и zK) в зависимости от угла поворота кривошипа 2 (α1).

Таблица 1.

Численные значения переменных параметров (α2, α3, α4 и B) в зависимости от угла поворота кривошипа (α1) для 12 положений механизма

                      α1, град
0 30 60 90 120 150 180 210 240 270 300 330
α2, град 7.01 38.29 74.38 114.51 150.31 181.31 209.05 234.31 259.03 283.32 308.43 334.58
α3, град 229.05 328.36 406.03 441.43 414.36 338.46 246.37 163.07 104.57 82.18 98.32 150.21
α4, град 6.49 9.31 16.21 24.51 31.19 33.15 31.25 27.16 21.58 16.24 11.28 7.58
В, мм 189.85 166.02 147.68 139.55 146.29 163.94 185.66 205.23 219.26 224.78 220.84 208.63
Таблица 2.

Численные значения координат точки R(xR, yR, zR) элемента 4' и точки K(yK, zK) винтового шатуна 3 в системе O1x1y1z1 в зависимости от угла поворота кривошипа (α1) для 12 положений механизма

  α1, град
0 30 60 90 120 150 180 210 240 270 300 330
xR, мм –24.74 9.98 6.33 –6.34 3.67 11.79 –18.78 –31.66 –15.28 –6.27 –12.76 –29.34
yR, мм 287.44 283.77 267.61 247.97 235.88 246.47 256.42 250.00 254.18 265.19 274.51 282.31
zR, мм 57.08 67.07 105.19 122.07 124.85 103.83 90.93 110.31 118.33 111.68 104.43 87.56
yK, мм 285.53 305.41 312.85 303.17 282.82 263.57 249.12 239.46 235.36 238.27 248.64 265.42
zK, мм 74.33 96.51 100.98 122.54 123.51 124.99 111.21 97.32 86.77 79.97 76.04 73.71

Таким образом, задача определения положения точек R и K разрешена. Скорости и ускорения данных точек могут быть определены путем дифференцирования координат по времени.

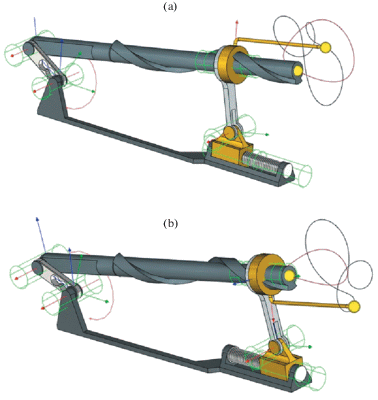
4. Визуализация и расчет траекторий движения выходного звена. В соответствии с кинематической схемой механизма для обработки внутренних поверхностей, приведенной на рис. 1, а также с учетом размеров звеньев механизма, приведенных в разделе 3, была разработана трехмерная параметрическая модель для визуализации траекторий движения точек R и K. На рис. 2 представлены трехмерные модели исследуемого механизма, когда ползун 6 находится в крайнем левом положении при длине стойки l1 = = 186 мм (рис. 2a) и когда ползун 6 находится в крайнем правом положении при длине стойки l1 = 241 мм (рис. 2б). На обоих рисунках также представлены воспроизводимые траектории движений точек R и K. Отметим, что при смещении ползуна 6, т.е. при изменении длины стойки 1, траектории указанных точек имеют разный характер.

Рис. 2.

Механизма для обработки внутренних поверхностей с воспроизводимыми траекториями движения точек R и K: (a) когда ползун 6 в крайнем левом положении при l1 = 186 мм; (б) когда ползун 6 в крайнем правом положении при l1 = 241 мм.

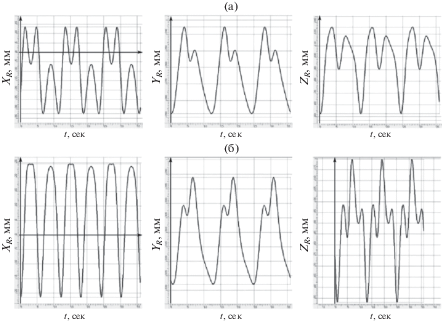
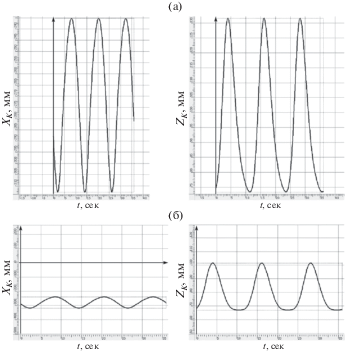
Это подтверждается также и графиками изменения координат данных точек от времени, приведенными на рис. 3a и 4a для модели, когда ползун 6 находится в крайнем левом положении, и на рис. 3б и 4б для модели, когда ползун 6 находится в крайнем правом положении.

Рис. 3.

Графики изменения координат (xR, yR, zR) точки R элемента 4' от времени (t): (a) для случая по рис. 2a; (б) для случая по рис. 2б.

Рис. 4.

Графики изменения координат (yK, zK) точки K винтового шатуна 3 от времени (t): (a) для случая по рис. 2a; (б) для случая по рис. 2б.

5. Заключение. В настоящем исследовании решены задачи структурного и кинематического анализа пятизвенного пространственного механизма для обработки внутренних поверхностей. Определена подвижность механизма с учетом входящих в его состав кинематических цепей с разным числом общих наложенных связей. Определены переменные углы наклона звеньев и смещения в кинематических парах, а также координаты, определяющие положение обрабатывающего элемента в пространстве в зависимости от положения ведущего звена. На основе кинематической схемы исследуемого механизма была разработана его трехмерная параметрическая модель и получены траектории движения выходного звена при изменении длины стойки механизма, которая варьируется за счет подвижной опоры коромысла. Проведен сравнительный анализ траекторий движения звеньев механизма путем сопоставления графиков изменения координат от времени. Исследованный механизм может найти широкое применение не только в обрабатывающих устройствах, но также и в смесительных системах, в машинах по лазерной резке и при вычерчивании пространственных кривых.

Финансирование. Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-31-00440.

Конфликт интересов. Авторы заявляют об отсутствии конфликта интересов.

Список литературы

  1. Глазунов В.А., Данилин П.О., Левин С.В., Тывес Л.И., Шалюхин К.А. Разработка механизмов параллельной структуры с кинематической и динамической развязкой // Ж. Проблемы машиностроения и надежности машин. 2010. № 2. С. 23.

  2. Хейло С.В., Глазунов В.А., Ширинкин М.А., Календарев А.В. Возможные применения механизмов параллельной структуры // Ж. Проблемы машиностроения и надежности машин. 2013. № 5. С. 19.

  3. Fomin A., Ivanov W., Paik J. Design of five-bar screw-lever manipulator and optimization of its output link path of motion. // Procedia Engineering. 2017. V. 206. P. 1703.

  4. Fomin A., Dvornikov L., Paik J. Calculation of the general number of imposed constraints of kinematic chains // Procedia Engineering. 2017. V. 206. P. 1309.

  5. Глазунов В.А., Ласточкин А.Б., Шалюхин К.А., Данилин П.О. К анализу и классификации устройств относительного манипулирования // Ж. Проблемы машиностроения и надежности машин. 2009. № 4. С. 81.

  6. Фомин А.С. Разработка методов структурного синтеза, кинематического и кинетостатического анализа механизмов второго семейства: автореф. дис. … канд. техн. наук. Омск. ОмГТУ. 2013. С. 20.

  7. Глазунов В.А., Левин С.В., Шалюхин К.А., Хаккыоглу М., Во Динь Тунг. Разработка механизмов параллельной структуры с четырьмя степенями свободы и частичной развязкой // Ж. Проблемы машиностроения и надежности машин. 2010. № 5. С. 3.

  8. Fomin A., Dvornikov L., Paramonov M., Jahr A. To the theory of mechanisms subfamilies. IOP Conference Series // Materials Science and Engineering. V. 124 (1). 012055.

  9. Briot S., Glazunov V., Arakelian V. Investigation on the effort transmission in planar parallel manipulators // Journal of Mechanisms and Robotics. 2013. V. 5(1).

  10. Хейло С.В., Глазунов В.А., Кулемкин Ю.В., Эфрос В.Л. Анализ ускорений и нелинейных колебаний сферического механизма параллельной структуры // Ж. Проблемы машиностроения и надежности машин. 2013. № 3. С. 9.

  11. Баклушин Д.С. Разработка методов структурного и кинематического синтеза клиновых и винтовых механизмов четвертого семейства: автореф. дис. … канд. техн. наук. Омск, ОмГТУ 2007. С. 21.

  12. Фомин А.С., Парамонов M.E. РФ Патент 161687, 2016.

  13. Хейло С.В., Глазунов В.А., Во Динь Тунг. Решение задачи о скоростях и особых положениях сферического манипулятора параллельной структуры // Ж. Машиностроение и инженерное образование. 2011. № 1. С. 18.

  14. Rashoyan G.V., Lastochkin A.B., Glazunov V.A. Kinematic analysis of a spatial parallel structure mechanism with a circular guide // Journal of Machinery Manufacture and Reliability. 2015. V. 44. № 7. P. 54.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал