1. На главную
  2. Электронные версии
  3. Проблемы машиностроения и надежности машин
  4. № 4, 2019

Проблемы машиностроения и надежности машин, 2019, № 4, стр. 3-13

РАЗРАБОТКА И РЕШЕНИЕ ЗАДАЧИ О ПОЛОЖЕНИЯХ МЕХАНИЗМА ПАРАЛЛЕЛЬНО-ПОСЛЕДОВАТЕЛЬНОЙ СТРУКТУРЫ ДЛЯ ХИРУРГИЧЕСКИХ ОПЕРАЦИЙ КАК АЛЬТЕРНАТИВЫ РОБОТУ DA VINCI

Е. И. Велиев 1, Р. Ф. Ганиев 2, В. А. Глазунов 2, Г. С. Филиппов 2, *, А. Н. Терехова 2

1 Российская медицинская академия непрерывного профессионального образования
Москва, Россия

2 Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия

* E-mail: filippov.gleb@gmail.com

Поступила в редакцию 11.03.2019
Принята к публикации 24.04.2019

Полный текст (PDF)

Аннотация

В статье проведен анализ робототехнической системы, являющейся альтернативой системы da Vinci. Приведена схема разработанного механизма параллельно-последовательной структуры. Решена задача о положениях.

Ключевые слова: малоинвазивная хирургия, роботическая система da Vinci, механизм параллельно-последовательной структуры, винтовое исчисление

Значение малоинвазивной хирургии, основанной на использовании манипуляционных систем (иногда подобные системы называют роботизированными или роботическими) и направленной на минимизацию области вмешательства в организм и степени травмирования тканей, возросло в последние несколько десятилетий. Основными преимуществами операций такого типа является уменьшение хирургических надрезов, снижение потерь крови и послеоперационных болей, сокращение времени пребывания в лечебных учреждениях [1–3]. В настоящее время широко применяется ручная лапароскопия, недостатки которой связаны с тем, что длительное пребывание в неудобных положениях повышает сложность работы хирурга и может снизить точность его действий. Применение ассистирующих роботов в малоинвазивной хирургии повышает маневрирующие возможности путем увеличения числа степеней свободы, решает проблему точки опоры и исключает дрожание рук [4].

Первым хирургическим роботом был разработанный около 30-ти лет назад робот PUMA 200 (Питтсбург, Пенсильвания), использовавшийся при биопсии головного мозга [5]. Затем роботизированная хирургия получила серьезное развитие [6–8]. Одним из наиболее известных устройств в этой области является система da Vinci Intuitive Surgical System. Она применяется в урологии, проктологии, гинекологии, кардиохирургии, эндокринологии и других медицинских областях [9–12]. В настоящее время существует третье поколение da Vinci Surgical System – Xi.

Согласно имеющимся сведениям, в мире используется более 4000 систем da Vinci Surgical System (все модели за все время), с применением которых проводится около 1 млн операций в год [13]. В России первый робот системы da Vinci появился в 2007 г. [14].

Следует отметить, что помимо высокой стоимости ($1.3–1.7 млн оборудование, около $150 000 годовое обслуживание, а также специальные одноразовые инструменты [15]) к недостаткам системы da Vinci Surgical System необходимо отнести чрезвычайно высокие соотношения массы механизма к полезной нагрузке, а также размеров звеньев к размеру рабочей зоны хирургического робота.

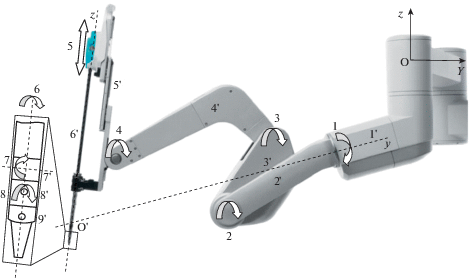
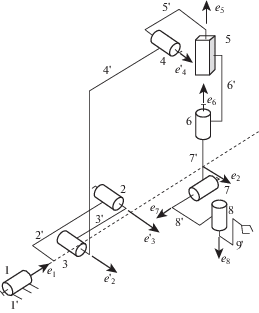
Проведем структурный анализ механизма роботизированной хирургической системы da Vinci. Рассмотрим общий вид данного манипулятора (рис. 1). Механизм содержит девять звеньев (1'–9'), одну поступательную (5) и восемь вращательных (1–4, 6–8) кинематических пар, причем схема имеет последовательную структуру (рис. 2). Используя формулу Сомова–Малышева, получим число степеней свободы механизма относительно неподвижного основания

(1)
$W = {\text{ }}6(n - 1) - 5{{p}_{5}} - 4{{p}_{4}} - 3{{p}_{3}} - 2{{p}_{2}} - {{p}_{1}} = 6(9 - 1) - 5 \cdot 8 = 8,$
где $W$ – число степеней свободы, $n$ – число звеньев кинематической цепи, ${{p}_{i}}$ – количество кинематических пар i-го класса (без учета подвижности губок схвата).

Рис. 1.

Один из манипуляторов da Vinci S.

Рис. 2.

Кинематическая схема одного из манипуляторов da Vinci S.

Согласно соотношению (1) механизм имеет восемь степеней свободы, хотя рабочий орган–инструмент обладает лишь шестью подвижностями. Дополнительные степени свободы необходимы для обеспечения постоянства точки ввода инструмента. Для этого используются вращения в кинематических парах 1–4 (рис. 1), где пара 1 дает вращение вокруг оси y, а пары 2–4 – вокруг перпендикулярной ей оси x, но с постоянной точкой пересечения осей O' (рис. 1).

Покажем наличие избыточности используемых в схеме приводов. Рассмотрим единичные винты, проходящие вдоль осей кинематических пар 2, 3, 4. Плюккеровы координаты единичных винтов осей кинематических пар в связанной с основанием неподвижной системе координат OXYZ в начальном положении будут ${\mathbf{e}}_{2}^{'}$ = $(1,0,0,0$, $y_{2}^{{'{^\circ }}}$, $z_{2}^{{'{^\circ }}})$; ${\mathbf{e}}_{3}^{'}$ = $(1,0,0,0$, $y_{3}^{{'{^\circ }}}$, $z_{3}^{{'{^\circ }}})$; ${\mathbf{e}}_{4}^{'}$ = $(1,0,0,0$, $y_{4}^{{'{^\circ }}}$, $z_{4}^{{'{^\circ }}})$. Зададим единичный винт ${{{\mathbf{e}}}_{2}}$ = $(1,0,0,0$, $y_{2}^{{^\circ }}$, $z_{2}^{{^\circ }})$, где $y_{2}^{{^\circ }}$ и $z_{2}^{{^\circ }}$ находятся из системы уравнений

(2)
$\left\{ \begin{gathered} a + b + c = 1; \hfill \\ a \cdot y_{2}^{{'{^\circ }}} + b \cdot y_{3}^{{'{^\circ }}} + c \cdot y_{4}^{{'{^\circ }}} = y_{2}^{{^\circ }}; \hfill \\ a \cdot z_{2}^{{'{^\circ }}} + b \cdot z_{3}^{{'{^\circ }}} + c \cdot z_{4}^{{'{^\circ }}} = z_{2}^{{^\circ }}. \hfill \\ \end{gathered} \right.$
Видно, что при любых $y_{2}^{{^\circ }}$ и $z_{2}^{{^\circ }}$ решение системы (2) существует, а значит кинематические пары 2–4 могут быть заменены одной. Таким образом, три кинематические пары c приводами дают только одну степень свободы, а выходное звено (рабочий орган) имеет шесть степеней свободы.

Наличие последовательной схемы у робота da Vinci обусловило необходимость включения двух дополнительных кинематических пар с приводами. При этом каждый следующий привод располагается на конце предшествующего звена, и общая длина манипулятора составляет несколько метров (при размере рабочей зоны не более пятнадцати сантиметров). Общий вес одной “руки” составляет порядка 80 кг (при весе самого инструмента, размещенного на ее конце, порядка 20 г), что приводит к снижению позиционной точности [16–18]. Использование механизмов параллельной структуры должно уменьшить влияние этих недостатков [19, 20]. Упомянутые механизмы, в которых выходное звено связано с основанием несколькими кинематическими цепями, отличаются повышенными показателями по точности и грузоподъемности в сравнении с обычными роботами, имеющими последовательную структуру и воспринимающими нагрузку как консоль [21, 22].

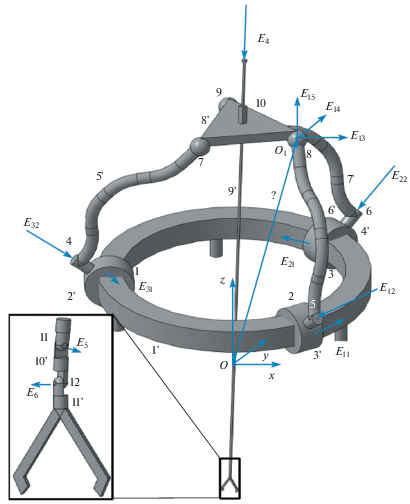
Предлагаемый механизм (рис. 3) имеет параллельную структуру и не требует избыточных приводов [23]. Он включает в себя три кинематические цепи, каждая из которых содержит приводную каретку, расположенную на круговой направляющей, вращательную кинематическую пару и сферическую кинематическую пару, связанную с подвижной платформой. При этом оси всех вращательных пар пересекаются в точке О. Кроме этого на подвижной платформе установлен линейный двигатель, ось которого проходит через точку О. Этот двигатель перемещает центральную штангу, на конце которой последовательно находятся две вращательных кинематических пары с перпендикулярными друг другу осями и инструмент. Центр О является точкой ввода инструмента.

Рис. 3.

Схема механизма с шестью степенями свободы для лапароскопических операций.

Проведем структурный анализ предлагаемого механизма. Он содержит одиннадцать звеньев (1'–11'), одну поступательную (10), восемь вращательных (1–6, 11–12) и три сферических (7–9) кинематических пар (рис. 3).

Используя формулу Сомова–Малышева, получим число степеней свободы механизма

$W = {\text{ }}6(n - 1) - 5{{p}_{5}} - 4{{p}_{4}} - 3{{p}_{3}} - 2{{p}_{2}} - {{p}_{1}} = 6(11 - 1) - 5 \times 9 - 3 \times 3 = 6.$

Покажем, что любые движения не меняют положения центра О. Для этого рассмотрим единичные винты, проходящие вдоль осей кинематических пар. Пусть с основанием связана неподвижная система координат OXYZ, центр которой совпадает с центром О. Тогда плюккеровы координаты единичных винтов кинематических цепей будут: E11 = E21 = E31 = (0, 0, 1, 0, 0, 0); E12 = (x12, y12, z12, 0, 0, 0 ); E13 = (1, 0, 0, 0, $y_{{13}}^{{^\circ }}$, $z_{{13}}^{{^\circ }}$); E14 = (0, 1, 0, $x_{{14}}^{{^\circ }}$, 0, $z_{{14}}^{{^\circ }}$); E15 = (0, 0, 1, $x_{{15}}^{{^\circ }}$, $y_{{15}}^{{^\circ }}$, 0); E22 = (x22, y22, z22, 0, 0, 0 ); E23 = (1, 0, 0, 0, $y_{{23}}^{{^\circ }}$, $z_{{23}}^{{^\circ }}$); E24 = (0, 1, 0, $x_{{24}}^{{^\circ }}$, 0, $z_{{24}}^{{^\circ }}$); E25 = (0, 0, 1, $x_{{25}}^{{^\circ }}$, $y_{{25}}^{{^\circ }}$, 0); E32 = (x32, y32, z32, 0, 0, 0 ); E33 = (1, 0, 0, 0, $y_{{33}}^{{^\circ }}$, $z_{{33}}^{{^\circ }}$); E34 = (0, 1, 0, $x_{{34}}^{{^\circ }}$, 0, $z_{{34}}^{{^\circ }}$); E35 = (0, 0, 1, $x_{{35}}^{{^\circ }}$, $y_{{35}}^{{^\circ }}$, 0).

Единичные винты обеспечивают движения платформы лишь вокруг точки О (сферические движения). Действительно, оси первых двух кинематических пар каждой цепи (E11, E21, E31) проходят через точку О и дают лишь вращения, а оси трех конечных вращательных пар, соответствующих сферическому шарниру, проходят через центр сферы и могут обусловить одно вращение, ось которого также проходит через центр О.

Обозначим вектор, соединяющий начало координат О и центр рассматриваемого шарнира О1, как ρ. При этом можно видеть, что $y_{{13}}^{{^\circ }}$ = ρz, $z_{{13}}^{{^\circ }}$ = ρy, $x_{{14}}^{{^\circ }}$ = ρz, $y_{{14}}^{{^\circ }}$ = ρx, $x_{{15}}^{{^\circ }}$ = ρy, $y_{{15}}^{{^\circ }}$ = ρx. Отсюда следует, что существует скользящий вектор, проходящий через центр О и имеющий нулевой момент относительно этого центра, т.е. определяет скорость в сферической паре. Подобные соотношения имеют место для всех трех кинематических цепей. В соответствии с этим, подвижная платформа совершает вращение лишь вокруг точки О, что обеспечивает постоянство центра введения инструмента.

Поскольку ось инструмента проходит через точку О, то движения вдоль оси инструмента, осуществляемые поступательным приводом расположенным на платформе, не меняют положение этой точки. В соответствии с этим, механизм обеспечивает сохранение центра ввода инструмента без наличия избыточности приводов, что выгодно отличает его от робота da Vinci. Кроме того, приводы установлены ближе к основанию, а кинематические цепи могут содержать лишь достаточно легкие звенья, что снижает вес и уменьшает габариты.

Описанный механизм можно использовать в хирургии не только как аналог лапароскопического инструмента, но и как устройство для перемещения видеокамеры, а также других вспомогательных инструментов. В Институте машиноведения им. А.А. Благонравова РАН изготовлен действующий макет подобного робота. В нем каретки сопрягаются с круговой направляющей посредством зубчатой передачи, а на каретках установлены двигатели, осуществляющие вращение приводных зубчатых колес.

Приведем сравнительную таблицу манипуляторов da Vinci и предлагаемого механизма, отражающую основные различия, являющиеся следствием применения принципиально разных структурных схем. Из табл. 1 следует, что предлагаемый механизм достаточно перспективен. Таким образом, проведен структурный анализ системы da Vinci Surgical System, предложена схема хирургического робота и представлен его прототип.

Таблица 1
  Кол-во степеней свободы (без учета инструмента) Кол-во приводов Вес без учета основания Размер рабочей области Позиционная точность Возможность увеличения рабочей нагрузки Независимость от импортных поставщиков и поддержки Использование стандартных лапароскопических инструментов
da Vinci S 6 8 ≈80 кг 15 см × 15 см × × 15 см 1.05 ± 0.24 мм Нет Нет Нет
предлагаемый механизм 6 6 ≈8 кг 15 см × 15 см × × 15 см 0.13 ± 0.03 мм Да Да Да

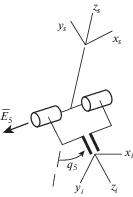
Для того, чтобы упростить конструкцию, не утратив функциональные свойства, можно устранить одну степень свободы, оставив лишь одно вращение инструмента относительно оси стержня – выходного звена сферического механизма параллельной структуры. При этом соответствующий узел рассматриваемого устройства может иметь две соосные вращательные кинематические пары, перемещающие губки схвата инструмента и задающие ось этого схвата (рис. 4).

Рис. 4.

Схват механизма с пятью степенями свободы.

Рассмотрим решение задачи о положениях для пятистепенного механизма, включающего трехподвижную сферическую часть с круговой направляющей (выходное звено этой части – стержень, установленный с возможностью перемещения вдоль его оси), а также вращательную кинематическую пару, ось которой перпендикулярна оси стержня. Положение рабочего органа задается матрицей Денавита–Хартенберга, где блок 3 × 3 соответствует направляющим косинусам, а четвертый столбец выражает координаты конца инструмента.

Система координат инструмента ОXiYiZi повернута вокруг оси х относительно системы координат, связанной с выходным звеном сферического механизма ОXsYsZs. Угол поворота отсчитывается от направления, противоположного оси zs и выражает координату q5, т.е. поворот происходит вокруг оси Е5 вращательной кинематической пары. Нужно найти координаты конца стержня выходного звена сферического механизма, определить положение оси zs сферического механизма и все углы поворота α, β, γ.

Матрицу положений инструмента можно представить следующим образом

$Ad{{\alpha }_{i}} = \left( {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&{\cos {{\alpha }_{i}}}&{ - \sin {{\alpha }_{i}}}&0 \\ 0&{\sin {{\alpha }_{i}}}&{\cos {{\alpha }_{i}}}&0 \\ 0&0&0&1 \end{array}} \right),\quad Ad{{\beta }_{i}} = \left( {\begin{array}{*{20}{c}} {\cos {{\beta }_{i}}}&0&{\sin {{\beta }_{i}}}&0 \\ 0&1&0&0 \\ { - \sin {{\beta }_{i}}}&0&{\cos {{\beta }_{i}}}&0 \\ 0&0&0&1 \end{array}} \right),$
$Ad{{\gamma }_{i}} = \left( {\begin{array}{*{20}{c}} {\cos {{\gamma }_{i}}}&{ - \sin {{\gamma }_{i}}}&0&0 \\ {\sin {{\gamma }_{i}}}&{\cos {{\gamma }_{i}}}&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{array}} \right),\quad Ad{{r}_{i}} = \left( {\begin{array}{*{20}{c}} 1&0&0&{{{x}_{i}}} \\ 0&1&0&{{{y}_{i}}} \\ 0&0&1&{{{z}_{i}}} \\ 0&0&0&1 \end{array}} \right),$
$A{{A}_{i}} = Ad{{r}_{i}} \cdot Ad{{\gamma }_{i}} \cdot Ad{{\beta }_{i}} \cdot Ad{{\alpha }_{i}},$
где xi, yi, zi – координаты конца инструмента, ${{\alpha }_{i}}$, ${{\beta }_{i}}$, ${{\gamma }_{i}}$ – углы его ориентации.

Найдем координаты конца стержня – выходного звена сферического механизма. Для этого необходимо вектор, длина которого равна длине инструмента, умножить на матрицу поворотов, соответствующую ориентации инструмента. Полученную матрицу смещений нужно умножить на матрицу ААi. В результате имеем вектор конца стержня – выходного звена сферической части механизма (четвертая строка – это вспомогательная единица)

$\left[ {\begin{array}{*{20}{c}} {{{x}_{i}} + {{d}_{i}}(\sin ({{\alpha }_{i}})\sin ({{\gamma }_{i}}) + \cos ({{\alpha }_{i}})\cos ({{\gamma }_{i}})\sin ({{\beta }_{i}}))} \\ {{{y}_{i}} - {{d}_{i}}(\cos ({{\gamma }_{i}})\sin ({{\alpha }_{i}}) - \cos ({{\alpha }_{i}})\sin ({{\beta }_{i}})\sin ({{\gamma }_{i}}))} \\ {{{z}_{i}} + {{d}_{i}}\cos ({{\alpha }_{i}})\cos ({{\beta }_{i}})} \\ 1 \end{array}} \right].$

Длина выдвижения стержня (координата q4)

$\begin{gathered} {{L}_{s}} = {{q}_{4}} = ({{[{{x}_{i}} + {{d}_{i}}(\sin ({{\alpha }_{i}})\sin ({{\gamma }_{i}}) + \cos ({{\alpha }_{i}})\cos ({{\gamma }_{i}})\sin ({{\beta }_{i}}))]}^{2}} + \\ + \;{{[{{y}_{i}} - {{d}_{i}}(\cos ({{\gamma }_{i}})\sin ({{\alpha }_{i}}) - \cos ({{\alpha }_{i}})\sin ({{\beta }_{i}})\sin ({{\gamma }_{i}}))]}^{2}} + \\ + \;{{[{{z}_{i}} + {{d}_{i}}\cos ({{\alpha }_{i}})\cos ({{\beta }_{i}})]}^{2}}{{)}^{{1/2}}}. \\ \end{gathered} $

Найдем координаты единичного вектора оси Zs(Xzs, Yzs, Zzs), совпадающей с осью стержня – выходного звена сферического механизма

${{X}_{{zs}}} = \frac{{{{x}_{i}} + {{d}_{i}}(\sin ({{\alpha }_{i}})\sin ({{\gamma }_{i}}) + \cos ({{\alpha }_{i}})\cos ({{\gamma }_{i}})\sin ({{\beta }_{i}}))}}{{{{L}_{s}}}},$
где две другие координаты Yzs и Zzs определяются аналогично.

Найдем координаты оси Xs(Xxs, Yxs, Zxs), связанной с выходным звеном сферического механизма ${{X}_{{xs}}}$ = $\cos ({{\beta }_{i}})$$\cos ({{\gamma }_{i}})$, координаты Yxs, Zxs определяются аналогично.

Координаты оси Ys(Xys, Yys, Zys), можно найти через векторное произведение двух найденных осей координатной системы

${{X}_{{ys}}} = {{Y}_{{zs}}}{{Z}_{{xs}}} - {{Y}_{{xs}}}{{Z}_{{zs}}},$
для нахождения Yzs и Zzs используем аналогичные соотношения.

Исходя из изложенного, путем приравнивания двух матриц, включающих углы αi, βi, γi и приведенные координаты, можно найти углы

$\beta = - \arcsin ({{Z}_{{xs}}});\quad \alpha = \arcsin \left( {\frac{{{{Z}_{{ys}}}}}{{\cos {{\beta }_{i}}}}} \right);\quad \gamma = \arcsin \left( {\frac{{{{Y}_{{xs}}}}}{{\cos {{\beta }_{i}}}}} \right).$

Приведем пример решения. Пусть углы ориентации инструмента αi= π/6 рад; βi = π/6 рад; γi= π/6 рад, а координаты конца инструмента xi = 0.09(м); yi = 0.06 (м); zi = 0.08 (м).

В этом случае матрица ААi имеет вид

$A{{A}_{i}} = \left( {\begin{array}{*{20}{c}} {0.75}&{ - 0.217}&{0.625}&{0.09} \\ {0.433}&{0.875}&{ - 0.217}&{0.06} \\ { - 0.5}&{0.433}&{0.75}&{0.08} \\ 0&0&0&1 \end{array}} \right).$

Вектор, характеризуемый длиной инструмента di = 0.1 умножаем на матрицу AAii

${{d}_{{ii}}} = {{\left( {\begin{array}{*{20}{c}} {6.25 \times {{{10}}^{{ - 3}}}}&{ - 2.165 \times {{{10}}^{{ - 3}}}}&{7.5 \times {{{10}}^{{ - 3}}}}&1 \end{array}} \right)}^{T}}.$

Отсюда вектор конца стержня-выходного звена сферического механизма

$\left[ {\begin{array}{*{20}{c}} {0.09 + 0.01\left( {\sin \left( {\frac{\pi }{6}} \right)\sin \left( {\frac{\pi }{6}} \right) + \cos \left( {\frac{\pi }{6}} \right)\cos \left( {\frac{\pi }{6}} \right)\sin \left( {\frac{\pi }{6}} \right)} \right)} \\ {0.06 - 0.01\left( {\cos \left( {\frac{\pi }{6}} \right)\sin \left( {\frac{\pi }{6}} \right) - \cos \left( {\frac{\pi }{6}} \right)\sin \left( {\frac{\pi }{6}} \right)\sin \left( {\frac{\pi }{6}} \right)} \right)} \\ {0.08 + 0.01\cos \left( {\frac{\pi }{6}} \right)\cos \left( {\frac{\pi }{6}} \right)} \\ 1 \end{array}} \right].$

Длина выдвижения стержня Ls, которая является четвертой обобщенной координатой q4, равна

${{L}_{s}} = {{q}_{4}} = 0.142\;{\text{м }}{\text{.}}$

Координаты единичных векторов осей Xs, Ys, Zs системы, связанной с выходным звеном сферического механизма, имеют значения: ${{X}_{{xs}}} = 0.75$; $Yxs = 0.433$; ${{Z}_{{xs}}} = - 0.5$; ${{X}_{{ys}}} = - 0.469$; ${{Y}_{{ys}}} = 0.799$; ${{Z}_{{ys}}} = - 0.012$; ${{X}_{{zs}}} = 0.676$; ${{Y}_{{zs}}} = 0.406$; $Zzs = 0.615$.

Используя приведенные соотношения, получаем

$\alpha = - 0.014\;{\text{р а д }};\quad \beta = 0.524\;{\text{р а д }};\quad \gamma = 0.524\;{\text{р а д }}.$

Для нахождения обобщенной координаты q5, рассмотрим оси координатных систем выходного звена сферического механизма и инструмента. Приравниваем две матрицы, одна из которых включает углы αi, βi, γi, а другая направляющие косинусы, т.е. координаты единичных векторов осей подвижной системы, связанной с инструментом в неподвижной системе координат. При этом имеем ${{X}_{{zi}}} = 0.625$ м; Yzi = –0.217 м; ${{Z}_{{zi}}} = 0.75$ м.

Координаты осей подвижной системы, связанной с выходным звеном сферического механизма, имеют следующие значения ${{X}_{{zs}}} = 0.676$, ${{Y}_{{zs}}} = 0.406$, ${{Z}_{{zs}}} = 0.615$ м. В соответствии с этим

${{q}_{5}} = \arccos [ - [{{X}_{{ys}}}{{X}_{{yi}}} + ({{Y}_{{ys}}}{{Y}_{{yi}}} + {{Z}_{{ys}}}{{Z}_{{yi}}})]],\quad {{q}_{5}} = 2.491\;{\text{р а д }}{\text{.}}$

Рассмотрим задачу о положениях сферической части механизма параллельно-последовательной структуры. Эта часть представляет собой сферический механизм с тремя кинематическими цепями и тремя степенями свободы. Примем следующие параметры кинематических цепей. Единичный вектор первой кинематической пары всех цепей имеет координаты ${{e}_{{11}}} = {{e}_{{21}}} = {{e}_{{31}}} = {{(\begin{array}{*{20}{c}} 0&0&1 \end{array})}^{T}}$. Единичные векторы второй и третьей кинематических пар второй кинематической цепи в начальном положении ${{e}_{{12}}} = {{(1,0,0)}^{T}}$, ${{e}_{{13}}} = {{\left( {\begin{array}{*{20}{c}} 0&{0.707}&{0.707} \end{array}} \right)}^{T}}$.

Силовой винт, передаваемый со стороны данной кинематической цепи на выходное звено в начальном положении, равен векторному произведению ${{r}_{1}} = {{e}_{{12}}}{{e}_{{13}}}$, ${{r}_{1}} = {{\left( {\begin{array}{*{20}{c}} 0&{ - 0.707}&{0.707} \end{array}} \right)}^{T}}$. Отметим, что в данном случае силовой винт – это чистый момент.

Вектор второй кинематической пары второй цепи ${{e}_{{22}}} = {{\left( {\begin{array}{*{20}{c}} { - 0.5}&{0.866}&0 \end{array}} \right)}^{T}}$.

Вектор третьей кинематической пары второй цепи повернут относительно вектора третьей кинематической пары первой кинематической цепи на угол 120°, следовательно, его координаты равны ${{e}_{{23}}} = {{\left( {\begin{array}{*{20}{c}} { - 0.612}&{ - 0.354}&{0.707} \end{array}} \right)}^{T}}$. Силовой винт (момент), передаваемый на выходное звено равен ${{r}_{2}} = {{e}_{{22}}}{{e}_{{23}}}$, ${{r}_{2}} = {{\left( {\begin{array}{*{20}{c}} {0.612}&{0.354}&{0.707} \end{array}} \right)}^{T}}$.

Аналогично для третьей кинематической цепи координаты единичных векторов второй и третьей кинематических пар равны

${{e}_{{32}}} = {{\left( {\begin{array}{*{20}{c}} { - 0.5}&{ - 0.866}&0 \end{array}} \right)}^{T}},\quad {{e}_{{33}}} = {{\left( {\begin{array}{*{20}{c}} {0.612}&{ - 0.354}&{0.707} \end{array}} \right)}^{T}}.$

Силовой винт (момент), передаваемый на выходное звено равен

${{r}_{3}} = {{e}_{{32}}}{{e}_{{33}}},\quad {{r}_{3}} = {{\left( {\begin{array}{*{20}{c}} { - 0.612}&{0.354}&{0.707} \end{array}} \right)}^{T}}.$

Для проверки, не является ли указанное положение особым, запишем определитель матрицы координат найденных моментов

$\left| r \right| = \left| {\begin{array}{*{20}{c}} 0&{0.612}&{ - 0.612} \\ { - 0.707}&{0.354}&{0.354} \\ {0.707}&{0.707}&{0.707} \end{array}} \right| = 0.918.$

Определитель отличен от нуля, положение не является особым.

Положение выходного звена описывается матрицей поворотов, полученной произведением матриц

${{A}_{\alpha }} = \left( {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos \alpha }&{ - \sin \alpha } \\ 0&{\sin \alpha }&{\cos \alpha } \end{array}} \right),\quad {{A}_{\beta }} = \left( {\begin{array}{*{20}{c}} {\cos \beta }&0&{\sin \beta } \\ 0&1&0 \\ { - \sin \beta }&0&{\cos \beta } \end{array}} \right),$
${{А }_{\gamma }} = \left( {\begin{array}{*{20}{c}} {\cos \gamma }&{ - \sin \gamma }&0 \\ {\sin \gamma }&{\cos \gamma }&0 \\ 0&0&1 \end{array}} \right),\quad {{A}_{A}} = {{A}_{\alpha }}{{A}_{\beta }}{{A}_{\gamma }}.$

Найдем координаты единичных векторов подвижных кинематических пар в произвольном положении. Для первой цепи текущее положение второй кинематической пары

$e{{t}_{{12}}} = {{\left( {\begin{array}{*{20}{c}} {\cos ({{\phi }_{{11}}})}&{\sin ({{\phi }_{{11}}})}&0 \end{array}} \right)}^{T}};$
где ${{\phi }_{{11}}}$ – угол поворота во входной кинематической паре.

Текущее положение единичного вектора третьей кинематической пары первой цепи определяется следующим образом

$e{{t}_{{13}}} = {{A}_{A}}{{e}_{{13}}} = \left( {\begin{array}{*{20}{c}} {0.707[\sin \gamma (\sin \alpha - \cos \alpha ) + \cos \gamma \sin \beta (\sin \alpha + \cos \alpha )]} \\ {0.707[\cos \gamma (\cos \alpha - \sin \alpha ) + \sin \gamma \sin \beta (\sin \alpha + \cos \alpha )]} \\ {0.707[\cos \beta (\sin \alpha + \cos \alpha )]} \end{array}} \right).$

Скалярное произведение векторов et12 и et13 равно нулю. Отсюда имеем

$\begin{gathered} \cos ({{\phi }_{{11}}})\frac{{\sqrt 2 }}{2}[\sin \gamma (\sin \alpha - \cos \alpha ) + \cos \gamma \sin \beta (\sin \alpha + \cos \alpha )] + \\ + \;\sin ({{\phi }_{{11}}})\frac{{\sqrt 2 }}{2}[\cos \gamma (\cos \alpha - \sin \alpha ) + \sin \gamma \sin \beta (\sin \alpha + \cos \alpha )] = 0. \\ \end{gathered} $

Согласно изложенному ϕ11 = q1

${{\phi }_{{_{{11}}}}} = {\text{arctg}}\left[ {\frac{{ - [\sin \gamma (\sin \alpha - \cos \alpha ) + \cos \gamma \sin \beta (\cos \alpha + \sin \alpha )]}}{{[\cos \gamma (\cos \alpha - \sin \alpha ) + \sin \gamma \sin \beta (\cos \alpha + \sin \alpha )]}}} \right].$

Для положения, когда α = 0, β = 0, γ = π/6, обобщенная координата ϕ11 = π/6 рад. Для второй цепи, используя аналогичный подход, имеем

$\begin{gathered} \cos ({{\phi }_{{21}}})\frac{{\sqrt 2 }}{4}[\sin \gamma (2\sin \alpha + \cos \alpha ) + \cos \gamma \sin \beta (2\cos \alpha - \sin \alpha ) - \sqrt 3 \cos \gamma \cos \beta ] + \\ + \;\sin ({{\phi }_{{21}}})\frac{{\sqrt 2 }}{4}[\cos \gamma (\cos \alpha - 2\sin \alpha ) + \sin \gamma \sin \beta (\sin \alpha + 2\cos \alpha ) - \sqrt 3 \sin \gamma \cos \beta ], \\ \end{gathered} $
где все обозначения аналогичны рассмотренным ранее.

Отсюда находим вторую обобщенную координату q2. Согласно тому, что скалярное произведение между векторами второй и третьей кинематических пар равно нулю ϕ21 = q2

${{\phi }_{{21}}} = {\text{arctg}}\left[ {\frac{{ - \left[ {\frac{{\sqrt 2 }}{4}[\sin \gamma (\sin 2\alpha + \cos \alpha ) + \cos \gamma \sin \beta (2\cos \alpha - \sin \alpha ) - \sqrt 3 \cos \gamma \cos \beta ]} \right]}}{{\frac{{\sqrt 2 }}{4}[ - \cos \gamma (\cos \alpha + 2\sin \alpha ) - \sin \gamma \sin \beta (\sin \alpha - 2\cos \alpha ) - \sqrt 3 \sin \gamma \cos \beta ]}}} \right] + \pi .$

В данном соотношении все обозначения аналогичны представленным ранее, слагаемое $\pi $ появилось вследствие того, что второй привод функционирует в соответствующем секторе круговой направляющей. При α = 0, β = 0, γ = π/6, обобщенная координата второй цепи ϕ21= 5π/6.

Для третьей кинематической цепи используем аналогичный подход и получаем ϕ31 = q3.

${{\phi }_{{31}}} = {\text{arctg}}\left[ {\frac{{ - \left[ {\frac{{\sqrt 2 }}{4}[\sin \gamma (\sin 2\alpha + \cos \alpha ) + \cos \gamma \sin \beta (2\cos \alpha - \sin \alpha ) + \sqrt 3 \cos \gamma \cos \beta ]} \right]}}{{\frac{{\sqrt 2 }}{4}[\sqrt 3 \sin \gamma \cos \beta - \cos \gamma (\cos \alpha + 2\sin \alpha ) - \sin \gamma \sin \beta (\sin \alpha + 2\cos \alpha )]}}} \right] + \pi .$

Для рассматриваемого примера ϕ31=3π/2 рад.

Таким образом, представлен механизм параллельно-последовательной структуры, являющийся альтернативой роботу da Vinci. Предложенный механизм отличается наличием части, имеющей параллельную структуру и содержащей три кинематические цепи, каждая из которых содержит приводную пару, перемещающуюся по круговой направляющей, а также две неприводные кинематические пары. Такая конструкция позволяет снизить габариты и вес при сохранении функциональных возможностей.

Финансирование. Работа выполнена при финансовой поддержке РФФИ, грант № 16-29-04273 офи_м.

Конфликт интересов. Авторы заявляют об отсутствии конфликта интересов.

Список литературы

  1. Minimally invasive surgery market–Global industry analysis, size, share, growth, trends & forecast, 2013–2019 // Transparency Market Research. Albany. NY. USA. Tech. Rep. 2014.

  2. Bonjer H.J. and Cancer Laparoscopic or Open Resection Study Group, Laparoscopic surgery versus open surgery for colon cancer: Short-term outcomes of a randomised trial // Lancet Oncol. 2005. V. 6. № 7. P. 477.

  3. Велиев Е.И., Голубцова Е.Н., Томилов А.А. Возможности малоинвазивной коррекции недержания мочи после радикального лечения рака предстательной железы // Ж. Онкоурология. 2013. № 4. С. 37.

  4. Ficarra V., Novara G., Fracalanza S. A prospective, non-randomized trial comparing robot-assisted laparoscopic and retropubic radical prostatectomy in one European institution // BJU Int. 2009. V. 104. № 4. P. 534.

  5. Kwoh Y.S., Hou J., Jonckheere E.A., Hayati S. A robot with improved absolute positioning accuracy for CT guided stereotactic brain surgery // IEEE Transactions on Biomedical Engineering. 1988. V. 35. № 2. P. 153.

  6. Sooriakumaran P., Srivastava A., Shariat S.F. A Multinational, Multiinstitutional Study Comparing Positive Surgical Margin Rates among 22393 Open, Laparoscopic, and Robot-assisted Radical Prostatectomy Patients // Eur Uro. 2014. V. 66. № 3. P. 450.

  7. Davis J., Kreaden U., Gabbert J., Thomas R. Perioperative outcomes of robot-assisted radical prostatectomy compared with open radical prostatectomy: results from the nationwide inpatient sample // J. Endourol. 2013.

  8. Maeso S., Reza M., Mayol J.A., Blasco J.A., Guerra M., Andradas E., Plana M.N. Efficacy of the da Vinci surgical system in abdominal surgery compared with that of laparoscopy: a systematic review and meta-analysis // Ann. Surg. 2010. V. 252. № 2. P. 254.

  9. Hubens G., Balliu L., Ruppert M., Gypen B., Van Tu T., Vaneerdeweg W. Roux-en-Y gastric bypass procedure performed with the da Vinci robot system: is it worth it // Surg Endosc. 2008. V. 22. № 7. P. 1690.

  10. Iselin C., Fateri F., Caviezel A., Schwartz J., Hauser J. Usefullness of the Da Vinci robot in urologic surgery // Rev Med Suisse. 2007. V. 5. № 3. P. 2766.

  11. Joseph R.A., Salas N.A., Johnson C., Goh A., Cuevas S.P., Donovan M.A., Kaufman M.G., Miles B., Reardon P.R., Bass B.L., Dunkin B.J. Video. Chopstick surgery: a novel technique enables use of the Da Vinci Robot to perform single-incision laparoscopic surgery // Surg. Endosc. 2010. V. 24. № 12. P. 3224.

  12. Morelli L., Guadagni S., Caprili G., Di Candio G., Boggi U., Mosca F. Robotic right colectomy using the Da Vinci Single-Site® platform: case report // Int. J. Med. Robot. 2013. V. 9. № 3. P. 258.

  13. Annual report 2017 (2018) Intuitive Surgical Inc.

  14. Краснопольский В.И., Попов А.А., Мананникова Т.Н., Федоров А.А., Слободянюк Б.А., Коваль А.А., Мироненко К.В. Робот-ассистированная хирургия в онкогинекологии // Ж. Онкогинекология. 2014. № 3. С. 23.

  15. Prewitt R., Bochkarev V., McBride C.L., Kinney S., Oleynikov D. The patterns and costs of the da Vinci robotic surgery system in a large academic institution // J. Robot. Surg. 2008. V. 2. P. 17.

  16. Kwartowitz D.M., Herrell S.D., Galloway R.L. Update: Toward image-guided robotic surgery: determining the intrinsic accuracy of the daVinci-S robot // Int. J. CARS. 2007. V. 1. P. 301.

  17. Kong N.J., Stephens T.K., Kowalewski T.M. Da Vinci Tool Torque Mapping over 50,000 Grasps and its Implications on Grip Force Estimation Accuracy // International Symposium on Medical Robotics (ISMR). 2018.

  18. Shawn Tsuda, Dmitry Oleynikov, et al. Davinci surgical system // SAGES Webmaster. 2015.

  19. Ганиев Р.Ф., Глазунов В.А. Манипуляционные механизмы параллельной структуры и их приложения в современной технике // Ж. ДАН. 2014. Т. 459. № 4. С. 1.

  20. Ганиев Р.Ф., Глазунов В.А. Перспективы теории машин в связи с развитием современного машиностроения // Ж. Справочник. Инженерный журнал с приложением. 2015. Т. 5 (218). С. 3.

  21. Чунихин А.Ю., Глазунов В.А. Разработка механизмов параллельной структуры с пятью степенями свободы, предназначенных для технологических роботов // Ж. Проблемы машиностроения и надежности машин. 2017. № 4. С. 3.

  22. Глазунов В.А., Борисов В.А., Левин С.В., Шалюхин К.А., Шарапов И.Б. РФ Патент 169275. Манипулятор параллельной структуры с пятью степенями степени подвижности.

  23. Велиев Е.И., Ганиев Р.Ф., Глазунов В.А., Филиппов Г.С. Параллельные и последовательные структуры манипуляторов в роботохирургии // Ж. ДАН. 2019. № 2.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал