Проблемы машиностроения и надежности машин, 2019, № 5, стр. 34-42
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ КОПИРУЮЩЕГО УПРАВЛЕНИЯ РОБОТОТЕХНИЧЕСКИМ УСТРОЙСТВОМ, ОСНАЩЕННЫМ ЛИНЕЙНЫМ ЭЛЕКТРОПРИВОДОМ С УПРУГИМ ЗВЕНОМ
А. В. Мальчиков 1, С. Ф. Яцун 1, *, А. С. Яцун 1
1 Юго-Западный Государственный университет
г. Курск, Россия
* E-mail: teormeh@inbox.ru
Поступила в редакцию 21.09.2018
Принята к публикации 25.06.2019
Аннотация
Статья посвящена разработке математической модели и исследованию копирующей системы управления робототехнического устройства, оснащенного линейным электроприводом с упругим звеном. Особое внимание уделено моделированию нелинейных свойств электропривода и измерительной системы. Разработан комплексный критерий оценки качественных показателей системы управления и изучены возможности минимизации влияния нелинейностей на устойчивость копирующей системы управления за счет оптимизации параметров.
Введение. Анализ современного состояния рассматриваемой проблемы. Начиная с 60-х годов ХХ века в зарубежных странах, и в России широкое распространение получили биотехнические системы управления, в которых манипулятор робота копирует движение руки или ноги оператора. Применение такого принципа управления, называемого копирующим, существенно расширяет функциональные возможности оператора, так как человек-оператор может выполнять движения, которые без робототехнического устройства он выполнить не в состоянии. Кроме того, управление может осуществляться на достаточно большом расстоянии от зоны выполнения работ, обеспечивая телеуправление роботом. Важным является и то, что задачи можно выполнять с масштабированием (например, смещение руки оператора на один сантиметр равно смещения манипулятора на один миллиметр и т.д.) [1].
Отдельно стоит выделить применение копирующих систем управления для задач так называемой носимой робототехники, в которой манипулятор робота совершает совместное движение с конечностями человека, усиливая или ускоряя работу мышц.
Однако, несмотря на наличие ряда публикаций [2–7], и реализованных систем с копирующей системой управления, методы исследования поведения КСУ с упругим элементом в приводе и синтеза параметров разработаны недостаточно.
Обоснование актуальности рассматриваемой проблемы. Одним из путей улучшения работы и повышения робастности копирующих систем управления (КСУ) является введение упругих элементов в электропривод, такие робототехнические системы, получили название эластичных или мягких роботов [8–13]. Такое техническое решение позволяет повысить эффективность и расширить область применения в первую очередь носимых робототехнических устройств, получивших название экзоскелеты, которые могут одеваться на несколько частей тела или на отдельную конечность [14, 15]. Однако, дальнейшее распространение этих устройств сдерживается из-за того, что копирующее управление, применяемое в таких устройствах, часто не обеспечивают необходимые показатели качества. Связано это с тем, что введение упругих элементов в КСУ с нелинейными элементами, присущими электроприводам и измерительной системе в определенных режимах изменяет характер поведения системы автоматического управления, снижает точность, увеличивает время переходных процессов, то есть, ухудшаются показатели качества системы управления, ее устойчивость [16]. Для выявления таких режимов необходимо разработать математическую модель копирующей системы управления и методику исследования устойчивости.
При исследовании устойчивости системы автоматического управления с несколькими нелинейными элементами, удобно применить метод, основанный на зондировании пространства варьируемых параметров, и определении времени переходного процесса путем решения нелинейных дифференциальных уравнений, численными методами в каждой точке гиперпространства. Для зондирования многомерного пространства применяются неравномерные сетки, проекции которых на любую грань гиперкуба, имеющую меньшую размерность, не приводят к значительному сокращению количества точек. В качестве последовательности точек используют последовательности случайных точек. Процедура случайного поиска представлена в ряде источников [17, 18]. Размерность пространства варьирования определяется вектором варьируемых параметров $\bar {a} \in {{R}^{N}}$, где N – число параметров, определяющих свойства КСУ.
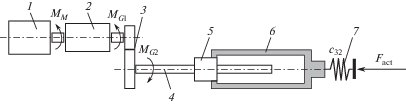
Изложение существа решения задачи. Расчетная схема. Одним из видов приводов, широко применяемых в робототехнике, являются линейные электроприводы, в основе которых лежит шарико-винтовая передача (ШВП), редуктор, электродвигатель. В зависимости от параметров такой трансмиссии, и в первую очередь шага ШВП, возможен режим функционирования, при котором реализуется эффект “самоторможение”, а также “сухое трение”. Кроме того, сам электродвигатель обладает нелинейными свойствами типа “зона нечувствительности и насыщение”. Копирующая система управления должна быть обеспечена системой связи человека и робота, чтобы движения оператора и машины были практически синхронны. Для этого КСУ оснащена датчиками перемещения или силы, а в ряде случаев и мускульной активности, которые передают информацию в бортовой вычислитель, который формирует управляющие воздействия, поступающие на приводы. Измерительная система КСУ, выполненная с использованием этих датчиков, так же обладает нелинейными свойствами типа “воздушный зазор”, “натяг”, “насыщение”. На рис. 1 приведена схема электропривода с упругим элементом, приводящего в движение звено робота.
На схеме: 1 – электродвигатель, развивающий крутящий момент ${{M}_{M}}$; 2 – редуктор с передаточным числом ${{k}_{{G1}}}$; 3 – цилиндрический редуктор с передаточным ${{k}_{{G2}}}$; 4 – винт шарико-винтовой передачи; 5 – гайка ШВП; 6 – исполнительное звено привода, 7 – дополнительный упругий элемент.
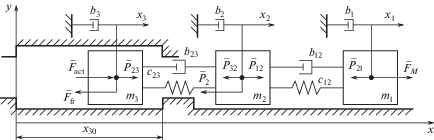
Математические модели элементов системы управления. Рассмотрим расчетную схему КСУ (рис. 2), которая состоит из трех твердых тел, связанных между собой упруго-вязкими элементами.
На схеме приняты следующие обозначения: масса ${{m}_{1}}$ – моделирует биологическое звено, ${{m}_{2}}$ – исполнительное звено робота, ${{m}_{3}}$ – исполнительное звено привода, ${{c}_{{12}}}$, ${{b}_{{12}}}$ – коэффициенты жесткости и вязкости измерительной системы; ${{c}_{{23}}}$, ${{b}_{{23}}}$ – коэффициенты жесткости и вязкости упругого элемента, соединяющего электропривод и исполнительное звено робота; ${{x}_{1}}$, ${{x}_{2}}$, ${{x}_{3}}$ – абсолютные координаты масс; ${{b}_{1}}$, ${{b}_{2}}$, ${{b}_{3}}$ – коэффициенты абсолютного вязкого сопротивления; ${{F}_{{{\text{act}}}}}$ – сила, развиваемая электроприводом; ${{F}_{{{\text{fr}}}}}$ – сила трения в механической передаче электропривода; ${{F}_{M}}$ – задающая сила, действующая на ${{m}_{1}}$ со стороны оператора; ${{P}_{{12}}} = {{P}_{{21}}}$ – сила, измеряемая датчиками измерительной системы; ${{P}_{{23}}} = {{P}_{{32}}}$ – сила упругого элемента, встроенного между исполнительным звеном электропривода и звеном робота; ${{P}_{2}}$ – сила, которую необходимо преодолеть при движении. На звено ${{m}_{1}}$ действуют силы ${{F}_{M}}$, ${{P}_{{12}}}$. На ${{m}_{2}}$ действуют силы ${{P}_{{12}}}$, ${{P}_{{32}}}$, ${{P}_{2}}$. На ${{m}_{3}}$ действуют ${{F}_{{{\text{act}}}}}$, ${{P}_{{23}}}$, ${{F}_{{{\text{fr}}}}}$. Кроме того, на все тела действуют силы вязкого сопротивления.
Математическую модель силы, развиваемой электроприводом, определим по формуле
(1)
${{F}_{{{\text{act}}}}} = \left\{ \begin{gathered} 0{\text{,}}\quad {\text{если}}\quad I < {{I}_{0}} \hfill \\ {{k}_{{{\text{act}}}}}I{\text{,}}\quad {\text{если}}\quad {{I}_{0}} < I < {{I}_{{\max }}} \hfill \\ {{k}_{{{\text{act}}}}}{{I}_{{\max }}}{\text{,}}\quad {\text{если}}\quad I > {{I}_{{\max }}} \hfill \\ \end{gathered} \right.,$В формуле (1) ${{I}_{0}}$ – минимальное значение тока электропривода, ${{I}_{{\max }}}$ – максимальный пусковой ток электропривода.
Силу сухого трения, определим по формуле
(3)
${{F}_{{{\text{fr}}}}} = \left\{ \begin{gathered} - F_{{{\text{fr}}}}^{{{\text{max}}}}{\text{sign}}({{{\dot {x}}}_{3}}),\quad {\text{если}}\quad {{{\dot {x}}}_{3}} \ne 0; \hfill \\ - \sum\limits_{j = 0}^n {F_{j}^{{m3}}} ,\quad {\text{если}}\quad {{{\dot {x}}}_{3}} = 0\quad {\text{и}}\quad \left| {\sum\limits_{j = 0}^n {F_{j}^{{m{\text{3}}}}} } \right| \leqslant F_{{{\text{fr}}}}^{{{\text{max}}}}; \hfill \\ - F_{{{\text{fr}}}}^{{{\text{max}}}}{\text{sign}}\left( {\sum\limits_{j = 0}^n {F_{j}^{{m3}}} } \right),\quad {\text{если}}\quad {{{\dot {x}}}_{3}} = 0\quad \left| {\sum\limits_{j = 0}^n {F_{j}^{{m3}}} } \right| > F_{{{\text{fr}}}}^{{{\text{max}}}}. \hfill \\ \end{gathered} \right.$Запишем дифференциальное уравнение движения m3
(4)
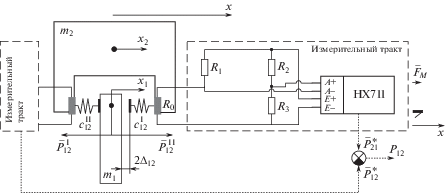
$\begin{gathered} m{{{\ddot {x}}}_{{\text{3}}}} + b{{{\dot {x}}}_{3}} = {{Р}_{{32}}} - {{F}_{{{\text{fr}}}}} - \sum\limits_{j = 0}^n {G_{j}^{{m3}}} \\ {{{\dot {x}}}_{3}} = 0{\text{,}}\quad {\text{если}}\quad \left| {\sum\limits_{j = 0}^n {G_{j}^{{m3}}} } \right| > \left| {{{F}_{{{\text{act}}}}}} \right|{\text{,}}\quad {\text{sign}}\left( {\sum\limits_{j = 0}^n {G_{j}^{{m3}}} } \right) \ne {\text{sign(}}{{F}_{{{\text{act}}}}}{\text{)}}, \\ \end{gathered} $Теперь рассмотрим схему измерительной системы КСУ (рис. 3).
Измерительная схема КСУ состоит из двух тензорезистивных чувствительных элементов, каждый из которых установлен на упругом основании с жесткостями $c_{{12}}^{{\text{I}}}$ и $c_{{12}}^{{{\text{II}}}}$. Схема закрепления чувствительных элементов позволяет регулировать зазор ${{\Delta }_{{12}}}$ между ними и массой m1 (рис. 3).
Для оценки деформации каждого из двух тензорезисторов используется полумостовая схема, показанная на рис. 3. На схеме ${{R}_{0}}$ – измерительный тензорезистор; ${{R}_{1}}$, ${{R}_{2}}$, ${{R}_{3}}$ – компенсирующие резисторы. В качестве аналого-цифрового преобразователя используется специализированная микросхема HX711. Далее цифровые сигналы с обоих АЦП поступают на микроконтроллер, который формирует задающее воздействие для системы управления электроприводом, при этом выходная величина, используемая в САУ $\vec {P}_{{12}}^{{}}$, определяется как разность показаний с обоих АЦП датчиков (5)
(5)
$\vec {P}_{{12}}^{{}} = P_{{21}}^{{\text{I}}} - P_{{12}}^{{{\text{II}}}} = c_{{12}}^{{\text{I}}}({{x}_{1}} - {{x}_{2}}) - c_{{12}}^{{{\text{II}}}}({{x}_{2}} - {{x}_{1}})$Если датчики измерительной системы установлены с зазором, то считая жесткость обоих чувствительных элементов равными ${{c}^{1}}_{{12}} = {{c}^{2}}_{{12}} = {{c}_{{12}}}$, получим
(6)
${{P}_{{12}}} = \left\{ \begin{gathered} 0{\text{,}}\quad {\text{если}}\quad \left| {{{x}_{1}} - {{x}_{2}}} \right| < = {{\Delta }_{{12}}} \hfill \\ {{c}_{{12}}}(({{x}_{1}} - {{x}_{2}}) - {{\Delta }_{{12}}}{\text{sign}}({{x}_{1}} - {{x}_{2}})){\text{,}}\quad {\text{если}}\quad \left| {{{x}_{1}} - {{x}_{2}}} \right| > {{\Delta }_{{12}}}, \hfill \\ \end{gathered} \right.$Если ${{\Delta }_{{12}}} = 0$, то ${{P}_{{12}}} = {{c}_{{12}}}({{x}_{1}} - {{x}_{2}})$, следовательно любое перемещение оператора приводит к появлению измеряемой величины $\vec {P}_{{12}}^{{}}$.
Для зондирования пространства параметров вектора $\bar {a} \in {{R}^{N}}$ дифференциальные уравнения, описывающие движение рассматриваемой механической системы представим в виде
где(9)
${\mathbf{M}} = \left( {\begin{array}{*{20}{c}} {{{m}_{1}}}&0&0 \\ 0&{{{m}_{2}}}&0 \\ 0&0&{{{m}_{3}}} \end{array}} \right);\quad {\mathbf{X}} = \left( {\begin{array}{*{20}{c}} {{{x}_{1}}} \\ {{{x}_{2}}} \\ {{{x}_{3}}} \end{array}} \right);$(10)
$\Phi (X,\dot {X}) = \left( {\begin{array}{*{20}{c}} {{{P}_{{21}}} + {{b}_{1}}{{{\dot {x}}}_{1}}} \\ { - {{P}_{{12}}} + {{P}_{{32}}} + {{b}_{2}}{{{\dot {x}}}_{2}}} \\ { - {{F}_{{act}}} - {{P}_{{23}}} + {{F}_{{fr}}} + {{b}_{3}}{{{\dot {x}}}_{3}}} \end{array}} \right);$(11)
${\mathbf{Q}} = \left( {\begin{array}{*{20}{c}} {{{F}_{M}}} \\ {{{P}_{2}}} \\ 0 \end{array}} \right).$Для обобщения результатов исследования и оптимизации приведем систему уравнений (8) к безразмерному виду, для этого введем обозначения: $\tau = \frac{t}{T}$ – безразмерное время ($T$ – масштаб времени), ${{\bar {x}}_{i}} = \frac{{{{x}_{i}}}}{L}$ – безразмерное перемещение ($L$ – масштаб перемещения).
Тогда для сил ${{P}_{{12}}}$ и ${{P}_{{23}}}$ справедливы выражения
(12)
${{P}_{{12}}} = {{c}_{{12}}}({{x}_{1}} - {{x}_{2}}) = {{c}_{{12}}}L({{\bar {x}}_{1}} - {{\bar {x}}_{2}});$(13)
${{P}_{{23}}} = {{c}_{{23}}}({{x}_{2}} - {{x}_{3}}) = {{c}_{{23}}}L({{\bar {x}}_{2}} - {{\bar {x}}_{3}}).$Преобразовав систему (8), получим
(14)
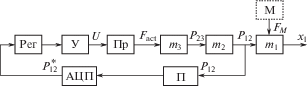
$\left\{ \begin{gathered} {{{\ddot {\bar {x}}}}_{1}} = {{{\bar {f}}}_{M}} - {\xi }_{{12}}^{2}({{{\bar {x}}}_{1}} - {{{\bar {x}}}_{2}}) - {{{\zeta }}_{1}}{{{\dot {\bar {x}}}}_{1}} \hfill \\ {{{\ddot {\bar {x}}}}_{2}} = {{{\bar {f}}}_{P}} - {{{\bar {m}}}_{{32}}}{\xi }_{{32}}^{2}({{{\bar {x}}}_{2}} - {{{\bar {x}}}_{3}}) + {{{\bar {m}}}_{{12}}}{\xi }_{{12}}^{2}({{{\bar {x}}}_{1}} - {{{\bar {x}}}_{2}}) - {{{\zeta }}_{2}}{{{\dot {\bar {x}}}}_{2}} \hfill \\ {{{\ddot {\bar {x}}}}_{3}} = {{{\bar {f}}}_{{{\text{act}}}}} - {{{\bar {f}}}_{{{\text{fr}}}}} + {\xi }_{{32}}^{2}({{{\bar {x}}}_{2}} - {{{\bar {x}}}_{3}}) - {{{\zeta }}_{3}}{{{\dot {\bar {x}}}}_{3}} \hfill \\ \end{gathered} \right.,$Структурная схема копирующей системы управления. Рассмотрим структурную схему копирующей системы управления электроприводом, приведенную на рис. 4, которая состоит из регулятора, усилителя, привода, исполнительного звена привода, исполнительного звена робота, биологического звена, преобразователя.
Сила ${{F}_{M}}$, создаваемая мышцами оператора создает перемещение биологического звена ${{m}_{1}}$. Силовой пропорционально диференцирующий (ПД) регулятор, формирует управляющее напряжение
(15)
${{u}^{{k + 1}}} = {{k}_{p}}(P_{{12}}^{k}) + {{k}_{d}}\left( {\frac{{P_{{12}}^{k} - P_{{12}}^{{k - 1}}}}{{\Delta t}}} \right),$Математическое моделирование. Обсуждение результатов в научном и прикладном аспектах. Полученная математическая модель управляемой электромеханической системы позволяет решить задачу оптимального синтеза параметров управляемой системы в следующей постановке. Получив значения ${{x}_{1}}$ и ${{x}_{2}}$, находим ошибку по положению ${\varepsilon } = {{x}_{1}} - {{x}_{2}}$ и устанавливаем параметры электропривода и регулятора позволяющие минимизировать ${\varepsilon }$. Введем три критерия эффективности работы системы: ${{K}_{{\text{I}}}}$ = = $\frac{1}{T}\int_0^T {\left| {{{x}_{1}} - {{x}_{2}}} \right|} dt$ – интегральный критерий ошибки; ${{K}_{A}} = \max ({{x}_{1}} - {{x}_{2}})$, $t \in [0,T]$ – амплитудный критерий ошибки; ${{K}_{{\text{Т}}}} = {{t}_{s}}$ – время переходного процесса, определяемого вхождением ошибки в 5% коридор от установившегося значения. В качестве целевой функции примем критерий, учитывающий и интегральную, амплитудную ошибку и время переходного процесса
(16)
$In = In(\bar {a}) = {{\alpha }_{{\text{1}}}}{{K}_{I}} + {{\alpha }_{{\text{2}}}}{{K}_{A}} + {{\alpha }_{{\text{3}}}}{{K}_{Т}},$Параметры, определяющие нелинейные свойства КСУ, можно разделить на неизменяемые, например массы, коэффициенты трения и т.д. и варьируемые, образующие вектор $\bar {a}$ = $({{k}_{{{\text{act}}}}}{{k}_{p}}{{k}_{d}}{{c}_{{12}}}{{c}_{{32}}})$. В пространстве этих параметров проведем серию вычислительных экспериментов для определения поверхности отклика $In$. Будем считать, что если $In < I{{n}_{0}}$, то система удовлетворяет требованиям устойчивости и точности. При моделировании были использованы следующие значения неизменяемых параметров двигателя (для коллекторного двигателя постоянного тока мощностью 60 Вт): ${{k}_{{{\text{act}}}}} = 6.8$; $R = 1.2$; $L = 0.008$, и механизма: ${{m}_{1}}$ = 10; ${{m}_{2}}$ = 25; ${{m}_{3}}$ = 2; ${{b}_{1}} = {{b}_{2}} = {{b}_{3}}$ = 100, ${{\Delta }_{{12}}}$ = = 0.002.
В качестве задающего усилия была использована прямоугольная функция, описываемая уравнением
(17)
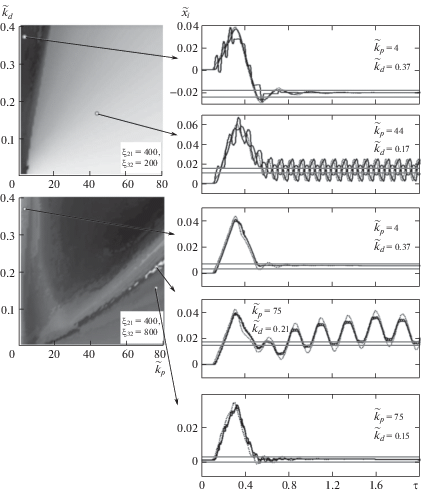
${{\bar {f}}_{M}} = \left\{ \begin{gathered} 0,\quad t \in {\text{[0,0}}{\text{.1)}} \hfill \\ {\text{100}},\quad t \in {\text{[0}}{\text{.1,0}}{\text{.3)}} \hfill \\ - {\text{100}},\quad t \in {\text{[0}}{\text{.3,0}}{\text{.5)}} \hfill \\ {\text{0}},\quad t \in {\text{[0}}{\text{.5,}} + \infty {\text{)}} \hfill \\ \end{gathered} \right.$На рис. 5 построены графики зависимости комплексного критерия $In(\bar {a})$ от значений коэффициентов kp, kd. На этих диаграммах определены области удовлетворительных в смысле критерия $In$ и неудовлетворительных режимов. Здесь же показаны примеры переходных процессов для устойчивых и неустойчивых режимов.
Рис. 5.
Комплексный параметр эффективности КСУ в области параметров ПД-регулятора и набор переходных характеристик при различных параметрах.
Для оценки размеров области удовлетворительности (устойчивости) системы, введем критерий качества управления ${\lambda } = {{S}_{1}}{\text{/}}{{S}_{0}}$, определяемый отношением количества экспериментов с устойчивым режимом к общему количеству вычислительных экспериментов (рис. 6). При этом, удовлетворительным режимом будем считать тот, при котором время переходного процесса ${{t}_{s}}$ меньше заданного. Также введем параметр ${{{\lambda }}_{m}}$ = ${\text{min}}({{S}_{1}}{\text{/}}{{S}_{0}})$, соответствующий минимуму отношения $\left( {{{S}_{1}}{\text{/}}{{S}_{0}}} \right)$ в исследуемом диапазоне значений безразмерной жесткости ${{{\xi }}_{{32}}}$. График этой величины в зависимости от безразмерной жесткости ${{{\xi }}_{{21}}}$ показан на рис. 6б.
Рис. 6.
Оценка влияния жесткостей упругого звена привода и жесткости измерительной системы на устойчивость системы: 1 – результаты для параметра ${{\xi }_{{12}}} = 150$; 2 – результаты для параметра ${{\xi }_{{12}}} = 200$; 3 – результаты для параметра ${{\xi }_{{12}}} = 400$; 4 – результаты для параметра ${{\xi }_{{12}}} = 800$.
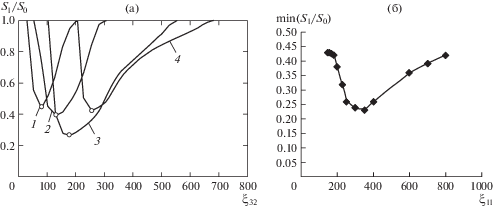
Анализ полученных диаграмм, представленных на рис. 6а показал, что величина области устойчивых режимов по отношению к общему числу ${\lambda } = {{S}_{1}}{\text{/}}{{S}_{0}}$ существенно зависит от величины жесткостей ${{{\xi }}_{{32}}}$ и ${{{\xi }}_{{21}}}$. Имеет место немонотонный характер изменения критериев ${\lambda }$ и ${{{\lambda }}_{m}}$. Область параметров с наименее удовлетворительными режимами определяется ${{{\xi }}_{{32}}} = 70{\kern 1pt} - {\kern 1pt} 350$ и ${{{\xi }}_{{21}}} = 350$ при ${{\Delta }_{{12}}} = 0.002$.
3аключение. В работе разработана математическая модель нелинейного электропривода копирующей системы управления с учетом нелинейных эффектов с неизменяемыми и варьируемыми параметрами. Предложен комплексный критерий оценки качества управления, учитывающий интегральную и максимальную ошибки, а также время переходного процесса. Особое внимание уделено исследованию влияния на качественные показатели системы управления, жесткости дополнительного упругого элемента, установленного в электроприводе и жесткости измерительной системы. Показано, что критерий качества управления ${\lambda } = {{S}_{1}}{\text{/}}{{S}_{0}}$ зависит от жесткости упругого элемента. На диаграмме оценки влияния жесткостей упругого звена привода и жесткости измерительной системы на устойчивость системы можно выделить три области: первая соответствует высокому уровню ${\lambda } = 1$ при малых значениях ${{{\xi }}_{{32}}}$ и с ростом ${{{\xi }}_{{21}}}$ эта область увеличивается, вторая – низкому $\lambda = 0.3{\kern 1pt} - {\kern 1pt} 0.4{\text{ }}$ при средних значениях ${{{\xi }}_{{32}}}$ и характеризуется смещением вправо при росте ${{{\xi }}_{{21}}}$; третья соответствует высокому уровню ${\lambda } = 1$ при больших значениях ${{{\xi }}_{{32}}}$. Минимальное значение критерия качества управления ${{{\lambda }}_{m}}$ зависит немонотонно от ${{{\xi }}_{{21}}}$ имея минимум при ${{{\xi }}_{{21}}} = 350$. В практическом плане установлена область параметров упругого подвеса, позволяющего обеспечить удовлетворительные показатели качества проектируемого устройства.
Список литературы
Furuta K. et al. Master-slave manipulator based on virtual internal model following control concept // Robotics and Automation. Proceedings. 1987 IEEE International Conference on. IEEE. 1987. V. 4. P. 567.
Pratt G.A., Williamson M.M. Series elastic actuators // Intelligent Robots and Systems 95. “Human Robot Interaction and Cooperative Robots”, Proceedings. 1995 IEEE/RSJ International Conference on. IEEE. 1995. V. 1. P. 399.
Robinson D.W. et al. Series elastic actuator development for a biomimetic walking robot // Advanced Intelligent Mechatronics, 1999. Proceedings. 1999 IEEE/ASME International Conference on. IEEE. 1999. P. 561.
Pratt G.A., Williamson M.M. Elastic actuator for precise force control, USA Patent 5650704, 1997.
Sakawa Y., Matsuno F., Fukushima S. Modeling and feedback control of a flexible arm // J. Robotic Systems. 1985. V. 2. № 4. P. 453.
De Luca A. Dynamic control of robots with joint elasticity // Robotics and Automation, 1988. Proceedings. 1988 IEEE International Conference on. IEEE. 1988. P. 152.
Spong M.W. Modeling and control of elastic joint robots // J. Dynamic Systems, Measurement, and Control. 1987. V. 109. № 4. P. 310.
Tomei P.A. Simple PD controller for robots with elastic joints // IEEE Transactions on Automatic Control. 1991. V. 36. № 10. P. 1208.
Keppler M., Lakatos D., Ott Ch., Albu-Scha¨ffer A. Elastic Structure Preserving (ESP) Control for Compliantly Actuated Robots IEEE TRANSACTIONS ON ROBOTICS.
Albu-Scha¨ffer A. et al. “Anthropomorphic soft robotics from torque control to variable intrinsic compliance,” in Robotics Research (Springer Tracts in Advanced Robotics), vol. 70, C. Pradalier, R. Siegwart, and G. Hirzinger, Eds. New York, USA: Springer, 2011. P. 185.
Ortega R., Kelly R., Loria A. A class of output feedback globally stabilizing controllers for flexible joints robots, IEEE Trans. Robot. Autom. 1995. V. 11. № 5. P. 766.
Albu-Scha¨ffer A., Hirzinger G. A globally stable state feedback controller for flexible joint robots, Adv. Robot. 2001. V. 15. № 8. P. 799.
Ott C. Cartesian Impedance Control of Redundant and Flexible-Joint Robots, B. Siciliano and O. Khatib, Eds. New York, USA: Springer, 2008.
Jatsun S. et al. Study of controlled motion of exoskeleton moving from sitting to standing position // Advances in Robot Design and Intelligent Control. Springer, Cham, 2016. P. 165.
Jatsun S., Savin S., Yatsun A. Parameter optimization for exoskeleton control system using sobol sequences // ROMANSY 21-Robot Design, Dynamics and Control. Springer, Cham, 2016. P. 361.
Westervelt E.R. et al. Feedback control of dynamic bipedal robot locomotion. CRC Press, 2007.
Растригин Л.А. Случайный поиск в задачах оптимизации многопараметрических систем. Рига: Изд-во Зинатне, 1965.
Курейчик В.М. Генетические алгоритмы // Ж. Известия Южного федерального университета. Технические науки. 1998. Т. 8. № 2.
Иванов Г.Г., Алфёров Г.В., Ефимова П.А. Устойчивость селекторно-линейных дифференциальных включений. Вестник пермского университета. 2017 Математика. Механика. Информатика Вып. 2(37) С. 25.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин