Проблемы машиностроения и надежности машин, 2019, № 5, стр. 59-69
АНАЛИЗ ЭФФЕКТИВНОСТИ РАВНОПРОЧНЫХ КОМПОЗИТНЫХ ЛИСТОВЫХ РЕССОР ПРИ РАЗЛИЧНЫХ УСЛОВИЯХ НАГРУЖЕНИЯ
А. Н. Полилов 1, *, Н. А. Татусь 1, Ш. Тян 2
1 Институт машиноведения им. А.А. Благонравова РАН
г. Москва, Россия
2 Xi’an Jiaotong University
г. Сиань, провинция Шэньси, Китай
* E-mail: polilovan@mail.ru
Поступила в редакцию 05.04.2018
Принята к публикации 25.06.2019
Аннотация
Для получения аналитических оценок возможного снижения массы рассматривается простейший случай консольной балки прямоугольного сечения, нагруженной сосредоточенной силой или распределенной нагрузкой. Выделены пять геометрических параметров проектирования, которые могут быть оптимально определены из пяти требований: по прочности, по возможной накопленной упругой энергии, по равнопрочности, по связи размеров сечения и по сопротивлению перерезывающей силе за счет известной прочности при межслойном сдвиге. Определены границы, за пределами которых линейная балочная теория приводит к некорректным результатам по прогибу равнопрочных балок при нагружении распределенными усилиями. Получены аналитические зависимости снижения требуемой массы равнопрочных балок от характера изменения приложенных усилий: чем более неравномерно изменяется приложенная нагрузка, тем большее преимущество по массе дает равнопрочное профилирование при заданных условиях по прочности и накопленной упругой энергией.
Введение. Балки равного сопротивления (equistrong – “равнопрочные”) исследовали со времен Галилея, но в учебной литературе по сопротивлению материалов и строительной механике обсуждается лишь простейшая треугольная форма, соответствующая условию равнонапряженности при изгибе сосредоточенной силой. Такой ограниченный интерес к равнопрочным балкам связан со сложностью их изготовления из стали. Наиболее известное применение нашли, по сути, треугольные балки в виде многолистовых рессор, в которых длина листов изменяется по линейному закону. Без учета трения такие рессоры соответствуют треугольной балке со ступенчатым изменением ширины. Скругляя концы листов, можно уменьшить размер “ступенек”, приближая по упругим свойствам многолистовую рессору к треугольной широкой балке постоянной толщины. Профилирование листов до равнопрочного профиля позволило бы перейти к, так называемым, малолистовым рессорам, когда равнопрочность достигается профилированием каждого листа (в идеале – единственного листа (12)), а не изменением длин листов. Но полноценное профилирование стальных листов – процедура крайне энергоемкая. Появление волокнистых композитов изменило ситуацию и возродило до этого абстрактный интерес к равнопрочным балкам [1–5], так как, в отличие от работы с металлами, изготовление “ажурной” композитной рессоры любого профиля не требует дополнительных усилий [6]. Так же как в природе без энергозатрат создаются сложные профилированные или ветвящиеся структуры (крона дерева, плавник рыбы, крыло бабочки) [7], так и композитные технологии: пултрузии (pulltrusion), пулформинга (pull-forming) и др. позволяют сравнительно легко получить любое изменение профиля.
Несмотря на кажущуюся изученность равнопрочных профилей, при анализе прогибов возникают неожиданные противоречия, и можно сформулировать дополнительные ограничения применимости балочного приближения для равнопрочных профилей, кроме традиционных требований малости: прогибов и углов поворота сечений.
В отличие от традиционных подходов строительной механики балка в настоящем изложении рассматривается не только как несущий брус, но и как листовая пружина, призванная запасать заданную упругую энергию [8]. Существенным усложнением анализа является необходимость учета влияния концевых участков с различной (для разных типов балок) длиной, определяемой площадью сечения на этих участках, достаточной для сопротивления перерезывающей силе, которое для композитов связано с межслойной сдвиговой прочностью [9].
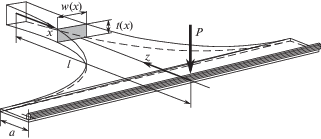
Постановка задачи. Рассматривается изгиб консольной балки фиксированной длины $l$ (length) с прямоугольным сечением, толщина t (thickness) и ширина w (width) которого принимаются изменяющимися по степенным законам, что правомерно, если изгибающий момент также изменяется по степенному закону
(1)
${\text{При}}\quad x \leqslant l - {{a}_{i}} \Rightarrow {{w}_{i}}(x) = {{w}_{i}}(0){{z}^{{{{\alpha }_{i}}}}};\quad {{t}_{i}}(x) = {{t}_{i}}(0){{z}^{{{{\beta }_{i}}}}};\quad z = 1 - x{\text{/}}l.$(2)
$\begin{gathered} {\text{При}}\quad x \in [l - {{a}_{i}};l] \Rightarrow {{w}_{i}}(x) = {{w}_{i}}(l - {{a}_{i}}) = {{w}_{i}}(0)a{{_{i}^{{\text{*}}}}^{{{{\alpha }_{i}}}}}; \\ {{t}_{i}}(x) = {{t}_{i}}(l - {{a}_{i}}) = {{t}_{i}}(0)a{{_{i}^{{\text{*}}}}^{{{{\beta }_{i}}}}};\quad a_{i}^{{\text{*}}} = {{a}_{i}}{\text{/}}l. \\ \end{gathered} $В качестве наглядных примеров в первых трех параграфах рассмотрены три простейших вида нагружения (обозначены римскими цифрами на рис. 1):
Рис. 1.
Виды нагрузок: I – сосредоточенная; II – равномерно распределенная; III – линейно убывающая.

концевая сосредоточенная сила; равномерно распределенная нагрузка; линейно убывающая распределенная нагрузка.
В реальности возможны различные комбинации этих нагрузок, но “красивых” аналитических решений для комбинированного нагружения равнопрочных балок получить не удается. Первый случай нагружения сосредоточенной силой – самый простой и практически наиболее важный для упругих элементов. Второй случай равномерно распределенной нагрузки ненамного сложнее, и он соответствует нагружению мостов, строительных конструкций или ветровым нагрузкам на крону дерева. Третий случай призван пояснить возникающие противоречия в вычислении прогибов по балочной теории, которые проанализированы в п. 4, чтобы затем перейти к общему энергетическому анализу возможного повышения весовой эффективности профилированных рессор.
1. Вид I – нагружение сосредоточенной силой (один верхний штрих) (рис. 1, I).
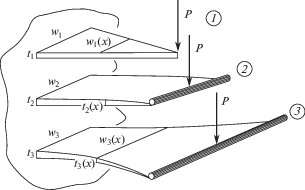
Индекс i в (1), (2) и далее означает тип балки (рис. 2): i = 0 – с постоянными размерами сечения; i = 1 – с постоянной толщиной; i = 2 – с постоянной шириной; i = 3 – с постоянной площадью поперечного сечения (constarea – “констэра”).
Рис. 2.
Три наиболее распространенных типа профилированных равнопрочных балок для нагружения концевой силой: треугольная – с постоянной толщиной –1; параболическая – с постоянной шириной – 2; констэра – с постоянной площадью сечения – 3.
В степенных зависимостях (1)–(2) при фиксированной длине $l$ содержатся пять параметров проектирования: начальные размеры сечения ${{w}_{i}}(0)$; ${{t}_{i}}(0)$, показатели ${{\alpha }_{i}}$; ${{\beta }_{i}}$ в законах их изменения (1) и длина концевого участка ${{a}_{i}}.$ Чтобы их однозначно определить, нужно чтобы проект балки удовлетворял пяти условиям:
1. Заданной жесткости $C$ – т.е. заданным отношением нагрузки Р к прогибу на конце $v_{i}^{{\text{'}}}(l)$
(3)
$C = \frac{P}{{{v}_{i}^{{\text{'}}}(l)}} = \frac{{E{{w}_{i}}(0)t_{i}^{3}(0)}}{{4\delta _{{{v}i}}^{'}{{l}^{3}}}};\quad \delta _{{{v}i}}^{{\text{'}}} = \frac{{{v}_{i}^{'}(l)}}{{{v}_{0}^{'}(l)}} = \frac{1}{{1 - {{\alpha }_{i}}{\text{/}}3 - {{\beta }_{i}}}}.$Коэффициент формы по прогибу $\delta _{{vi}}^{{\text{'}}}$ равен отношению максимального прогиба на конце профилированной балки к прогибу $v_{0}^{{\text{'}}}(l)$ прямоугольной балки с теми же размерами ${{w}_{i}}(0)$; ${{t}_{i}}(0)$ корневого сечения; штрих означает нагружение концевой силой – вид I.
2. Заданной прочности ${{\sigma }_{{\text{*}}}}$ (способностью выдержать заданную нагрузку ${{P}_{{\max }}}$)
(4)
$\frac{{6{{P}_{{{\text{max}}}}}l}}{{{{w}_{i}}(0)t_{i}^{2}(0)}} = {{\sigma }_{{{\text{max}}}}} \leqslant {{\sigma }_{{\text{*}}}}.$3. “Равнопрочности”
(5)
$\frac{{6P(l - x)}}{{{{w}_{i}}(x)t_{i}^{2}(x)}} = \frac{{6Pl}}{{{{w}_{i}}(0)t_{i}^{2}(0)}};\quad из\quad {\text{(1)}} \Rightarrow {{\alpha }_{i}} + 2{{\beta }_{i}} = 1.$4. Выбранного соотношения между размерами сечения. Тут возможно бесконечное число вариантов, но три типа балок наиболее естественны:
4.1. Постоянная толщина ${{t}_{1}}(0) = {\text{const}}$ ⇒ ${{\beta }_{1}} = 0$; ${{\alpha }_{1}} = 1$. Это условие связано с простотой получения упругого элемента, например, из стального листа;
4.2. Постоянная ширина ${{w}_{2}}(0) = {\text{const}}$ ⇒ ${{\alpha }_{2}} = 0$; ${{\beta }_{2}} = \frac{1}{2}$. Это условие определяется, например, ограничениями на габариты рессоры в автомобиле;
4.3. Постоянная площадь поперечного сечения ${{w}_{3}}(x){{t}_{3}}(x)$ = ${{w}_{3}}(0){{t}_{3}}(0)$.
Это условие особенно важно для обеспечения прочности композитных балок, так как позволяет сохранять постоянное число неперерезанных волокон по всей длине рессоры.
Тип 4.3 балки констэра (рис. 3) из (1) означает
и из условия “равнопрочности” (5): ${{\alpha }_{3}} = - 1$; ${{\beta }_{3}} = 1$.5. Сопротивления перерезывающей силе ${{P}_{{{\text{max}}}}}$, приложенной на конце балки (для распределенной нагрузки это условие не обязательно, так как на свободном конце перерезывающая сила равна нулю). Примем это условие в виде достижения межслойными касательными напряжениями критического значения ${{\tau }_{{\text{*}}}}$, тогда оно определяет длину а (2) концевого участка, площадь сечения которого должна сохраняться постоянной
(7)
${{w}_{i}}(l - {{a}_{i}}){{t}_{i}}(l - {{a}_{i}}) = {{t}_{i}}(0){{w}_{i}}(0){{(a_{i}^{{\text{*}}})}^{{{{\alpha }_{i}} + {{\beta }_{i}}}}} = \frac{{3{{P}_{{\max }}}}}{{2\tau {\text{*}}}} = A.$В балке констэра (типа 3) площадь сечения считается постоянной, и расстояние а3 необходимо определять не по условию прочности на межслойный сдвиг (7), которое формально выполняется всюду, а через конструктивно допустимую ширину ${{w}_{{\text{*}}}}$.
Требуемая нормированная длина $a_{i}^{{\text{*}}}$ концевого участка для разных типов равнопрочных балок различна, и поэтому влияние “испорченных” концов на жесткость (а значит, и на прочность) будет различным, т.к. изменятся требуемые размеры корневого сечения. Задача становится связанной по всем пяти условиям, т.е. принципиально более сложной. Соответствующие “реальные” коэффициенты по прогибу $\delta _{{vi}}^{{\text{*}}}$ и по массе $\delta _{{mi}}^{{\text{*}}}$ помечены верхним индексом * (табл. 1).
Таблица 1.
Параметры “идеальных” и “реальных” (*) консольных балок при нагружении сосредоточенной силой (вид I)
| Индекс i | Тип балки | ${{\alpha }_{i}}$ | ${{\beta }_{i}}$ | $\delta _{{vi}}^{'}$ | $\delta _{{mi}}^{{\text{'}}}$ | $\delta _{{\Sigma i}}^{'}$ | $\delta _{{vi}}^{{\text{'}}}{\text{/}}\delta _{{vi}}^{{\text{'}}}$ | $\delta _{{mi}}^{{\text{'}}}{\text{/}}\delta _{{mi}}^{{\text{'}}}$ | $a_{i}^{{\text{*}}} = {{a}_{i}}{\text{/}}l$ |
|---|---|---|---|---|---|---|---|---|---|
| 0 | ${{t}_{0}}(x)$, ${{w}_{0}}(x) = {\text{const}}$ | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | ${{t}_{1}}(x) = const$ | 1 | 0 | 3/2 | 1/2 | 1/3 | 1 – $a_{1}^{{{\text{*}}2}}{\text{/}}3$ | 1 + $a_{1}^{{{\text{*}}2}}$ | $\frac{A}{{{{t}_{1}}(0){{w}_{1}}(0)}}$ |
| 2 | ${{w}_{2}}(x) = const$ | 0 | 1/2 | 2 | 2/3 | 1/3 | 1 – $a_{2}^{{{\text{*}}3/2}}{\text{/}}2$ | 1 + $a_{2}^{{{\text{*}}3/2}}{\text{/}}2$ | ${{\left( {\frac{A}{{{{t}_{2}}(0){{w}_{2}}(0)}}} \right)}^{2}}$ |
| 3 | ${{w}_{3}}(x){{t}_{3}}(x) = const$ | –1 | 1 | 3 | 1 | 1/3 | 1 – $2a_{3}^{{\text{*}}}{\text{/}}3$ | 1 | ${{w}_{3}}(0){\text{/}}{{w}_{{\text{*}}}}$ |
Для удовлетворения условия (3) по жесткости необходимо рассчитать прогиб консольной балки
(8)
$v{\text{'}}(l) = \frac{P}{E}\left[ {\int\limits_0^{l - a} {\frac{{{{{(l - x)}}^{2}}dx}}{{I(x)}} + } \int\limits_{l - a}^l {\frac{{{{{(l - x)}}^{2}}dx}}{{I(l - a)}}} } \right] = {{v}_{0}}\delta _{v}^{{\text{*}}};\quad I(x) = \frac{{w(x){{t}^{3}}(x)}}{{12}};$(9)
$\delta _{{vi}}^{{\text{*}}} = \delta _{{vi}}^{{\text{'}}}[1 - ({{\alpha }_{i}}{\text{/}}3 + {{\beta }_{i}}){{(a_{i}^{{\text{*}}})}^{{3 - {{\alpha }_{i}} - {\text{3}}{{\beta }_{i}}}}}].$Нижний индекс 0 относится к прогибу (8) и к массе (10) прямоугольной балки с теми же размерами $w(0)$; $t(0)$ корневого сечения.
Массу балки легко рассчитать через размеры корневого сечения, законы их изменения (1), (2) и плотность $\rho $
(10)
$\begin{gathered} m(l) = \rho \left[ {\int\limits_0^{l - {{a}_{i}}} {{{w}_{i}}(x){{t}_{i}}(x)dx + } \int\limits_{l - {{a}_{i}}}^l {{{w}_{i}}(l - {{a}_{i}}){{t}_{i}}(l - {{a}_{i}})dx} } \right] = {{m}_{0}}\delta _{{mi}}^{{\text{*}}}; \\ \delta _{{mi}}^{{\text{*}}} = {{\delta }_{{mi}}} + (1 - {{\delta }_{{mi}}}){{(a_{i}^{{\text{*}}})}^{{1/{{\delta }_{{mi}}}}}};\quad {{\delta }_{{mi}}} = \frac{1}{{1 + {{\alpha }_{i}} + {{\beta }_{i}}}};\quad {{m}_{0}} = \rho w(0)t(0)l. \\ \end{gathered} $Например, для балки констэра: $\delta _{{v3}}^{{\text{*}}} = 3 - 2{{a}_{3}}{\text{/}}l$, $\delta _{{m3}}^{*} = {{\delta }_{{m3}}} = 1$.
Требуемые размеры корневого сечения найдутся для выбранного типа балки (i) из одновременного выполнения условий по прочности (4) и по жесткости (3) с учетом (9)
(11)
${{t}_{i}}(0) = \frac{{2C{{\sigma }_{{\text{*}}}}{{l}^{2}}}}{{3E{{P}_{{{\text{max}}}}}}}\delta _{{vi}}^{{\text{*}}} = {{t}_{0}}\delta _{{vi}}^{{\text{*}}}{\text{,}}\quad {{w}_{i}}(0) = \frac{{27P_{{{\text{max}}}}^{3}{{E}^{2}}}}{{2\sigma _{{\text{*}}}^{3}{{C}^{2}}{{l}^{3}}\delta _{{vi}}^{{{\text{*2}}}}}} = \frac{{{{w}_{0}}}}{{\delta _{{vi}}^{{{\text{*2}}}}}}{\text{,}}$(12)
${{n}_{i}} = \frac{{27P_{{{\text{max}}}}^{3}}}{{2{{C}^{2}}{{l}^{3}}w{\text{*}}}}\frac{{{{E}^{2}}}}{{\sigma _{{\text{*}}}^{3}\delta _{{vi}}^{2}}}$Из (12) видно, что только за счет низкого модуля упругости однонаправленного стеклопластика (в 4.5 раза ниже, чем у стали) можно примерно в 20 раз снизить число листов, т.е. любую реальную стальную многолистовую рессору заменить не просто малолистовой, но однолистовой рессорой из стеклопластика.
Из (11) (или с учетом (9), (10)) легко рассчитать минимально возможную массу “идеальной” (или “реальной”) балки
(13)
$m(l) = \rho {{w}_{i}}(0){{t}_{i}}(0)l{{\delta }_{{mi}}} = \frac{{\rho {{w}_{0}}{{t}_{0}}l{{\delta }_{{mi}}}}}{{\delta _{{{v}i}}^{{\text{'}}}}} = \frac{{9\rho P_{{\max }}^{2}E}}{{\sigma _{{\text{*}}}^{2}C}}\delta _{\Sigma }^{{\text{'}}},$Интересный вывод получается из (13) с учетом выполнения условия равнопрочности (5): $\alpha + 2\beta = 1$. Коэффициент снижения массы для всех равнопрочных (при нагружении концевой силой) балок, имеющих заданную прочность и жесткость, одинаков
(14)
$\delta _{\Sigma }^{{\text{'}}} = \frac{{3 - \alpha - 3\beta }}{{3(1 + \alpha + \beta )}} = \frac{1}{3}.$2. Вид II – равномерно распределенная нагрузка (двойной штрих) (рис. 1, II). Перерезывающая сила на конце равна нулю, поэтому концевые участки с постоянной площадью сечения формально не нужны. Таким образом, остаются 4 параметра проектирования: два размера корневого сечения ${{w}_{i}}(0)$, ${{t}_{i}}(0)$ и два параметра ${{\alpha }_{i}}$; ${{\beta }_{i}}$ зависимостей (1).
Условие по прочности типа (4) примет вид $({{P}_{{{\text{max}}}}} = {{p}_{{{\text{max}}}}}l)$
(15)
$\frac{{3{{P}_{{{\text{max}}}}}l}}{{{{w}_{i}}(0)t_{i}^{2}(0)}} = {{\sigma }_{{{\text{max}}}}} \leqslant \sigma {\text{*}}{\text{.}}$Условие равнопрочности (5) с учетом (1) принимает иной вид
(16)
$\frac{{p{{{(l - x)}}^{2}}}}{{{{w}_{i}}(x)t_{i}^{2}(x)}} = \frac{{p{{l}^{2}}}}{{{{w}_{i}}(0)t_{i}^{2}(0)}} \Rightarrow {{\alpha }_{i}} + 2{{\beta }_{i}} = 2.$Для формулировки условия типа (3) по жесткости нужно найти прогиб на конце, для чего надо дважды проинтегрировать уравнение изгиба
(17)
$\begin{gathered} EI(x)\frac{{{{d}^{2}}v_{i}^{{''}}(x)}}{{d{{x}^{2}}}} = \frac{{{{l}^{2}}}}{2}p{{z}^{2}};\quad z = 1 - \frac{x}{l} \in [0;1]; \\ v_{i}^{{''}}(x) = \frac{{6p{{l}^{4}}}}{{E{{w}_{i}}(0)t_{i}^{3}(0)(3 - {{\alpha }_{i}} - 3{{\beta }_{i}})}}\left[ {1 - z + \frac{{{{z}^{{4 - {{\alpha }_{i}} - 3{{\beta }_{i}}}}} - 1}}{{4 - {{\alpha }_{i}} - 3{{\beta }_{i}}}}} \right] \Rightarrow \frac{{v_{i}^{{''}}(l)}}{{v_{0}^{{''}}(l)}} = \delta _{{vi}}^{{''}}\frac{4}{{(4 - {{\alpha }_{i}} - 3{{\beta }_{i}})}}, \\ \end{gathered} $(18)
$C = \frac{{pl}}{{v_{i}^{{''}}(l)}} = \frac{{2E{{w}_{i}}(0)t_{i}^{3}(0)}}{{3\delta _{{vi}}^{{''}}{{l}^{3}}}}.$Показатели степенных зависимостей (1), коэффициенты формы по прогибу (17) и по массе (11) приведены в табл. 2 для рассматриваемых трех типов равнопрочных балок. Условия по прочности (15) и жесткости (18) совпадают с (4) и (3) с точностью до констант, поэтому вид формул (11) сохраняется, и по аналогии с (13) минимальная масса равномерно нагруженной, равнопрочной балки при заданных прочности и жесткости выражается в виде
(19)
$m(l) = \rho w(0)t(0)l{{\delta }_{{mi}}} = \frac{{6\rho p_{{\max }}^{2}{{l}^{2}}E}}{{\sigma _{{\text{*}}}^{2}C}}\delta _{{\Sigma i}}^{{''}};\quad \delta _{{\Sigma i}}^{{''}} = \frac{{\delta _{{mi}}^{{''}}}}{{\delta _{{vi}}^{{''}}}}.$Таблица 2.
Параметры “идеальных” равнопрочных консольных балок при нагружении равномерной нагрузкой (вид II)
| Индекс i | Тип балки | ${{\alpha }_{i}}$ | ${{\beta }_{i}}$ | $\delta _{{{v}i}}^{{''}}$ | $\delta _{{mi}}^{{''}}$ | $\delta _{{\Sigma i}}^{{''}}$ | $\delta _{{Ui}}^{{''}}$ | $\delta _{{Si}}^{{''}}$ |
|---|---|---|---|---|---|---|---|---|
| 1 | $t(x) = {\text{const}}$ | 2 | 0 | 2 | 1/3 | 1/6 | 5/3 | 1/5 |
| 2 | $w(x) = {\text{const}}$ | 0 | 1 | 4 | 1/2 | 1/8 | 5/2 | 1/5 |
| 3 | $w(x)t(x) = {\text{const}}$ | –2 | 2 | ∞ | 1 | 0 | 5 | 1/5 |
Однако, как видно из табл. 2, в отличие от (14) коэффициент $\delta _{{\Sigma i}}^{{''}}$ снижения массы (19) при заданном прогибе не остается одинаковым для разных типов равномерно нагруженных равнопрочных балок.
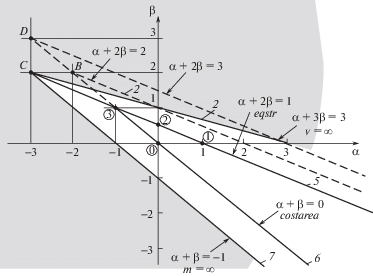
Значок $\infty $ в табл. 2 означает, что точка В с координатами $\alpha _{3}^{{''}} = - 2$; $\beta _{3}^{{''}} = 2$ выходит за пределы допустимого сектора на рис. 4, т.е. анализ прогиба в балочном приближении становится некорректен.
Рис. 4.
Допустимые законы изменения размеров сечения для консольных балок, нагруженных концевой сосредоточенной силой.
Мы приходим к выводу, что для распределенной нагрузки разумно задавать не условную жесткость, выраженную через максимальный прогиб, а возможную накопленную при изгибе упругую энергию. При этом не возникает противоречия со случаем сосредоточенной силы, так как при нагружении вида I возможная накопленная упругая энергия ${{U}_{{\text{*}}}}$ пропорциональна максимальному прогибу: $2{{U}_{{\text{*}}}} = {{P}_{{{\text{max}}}}}v{\text{'}}(l)$, и она однозначно связана с заданной жесткостью С.
При нагружении вида II упругая энергия равна интегралу от произведения распределенной нагрузки на переменный прогиб (17)
(20)
${{U}_{{\text{*}}}} = \frac{{3{{p}^{2}}{{l}^{5}}}}{{10Ew(0){{t}^{3}}(0)(1 - {{\alpha }_{i}}{\text{/}}5 - 3{{\beta }_{i}}{\text{/}}5)}} = U_{0}^{{{\text{''}}}}\delta _{{Ui}}^{{{\text{''}}}}.$Отношение $\delta _{{Ui}}^{{{\text{''}}}}$ (20) накопленной энергии в равнопрочной балке к энергии в прямоугольной балке с теми же размерами корневого сечения следует использовать в (19) вместо $\delta _{{vi}}^{{{\text{''}}}}$, и тогда корректный коэффициент снижения массы $\delta _{{Si}}^{{{\text{''}}}}$ при заданной упругой энергии ${{U}_{{\text{*}}}}$ примет для равнопрочных балок (16) следующий вид
(21)
$\delta _{{Si}}^{{{\text{''}}}} = \frac{{\delta _{{mi}}^{{{\text{''}}}}}}{{\delta _{{Ui}}^{{{\text{''}}}}}} = \frac{{5 - \alpha - 3\beta }}{{5(1 + \alpha + \beta )}} = \frac{{3 - \beta }}{{5(3 - \beta )}} = \frac{1}{5}.$Как видно из табл. 2, противоречие, которое обнаруживается при расчете прогиба “слишком” профилированных балок, снимается при интегральной оценке запасенной упругой энергии. Ситуация напоминает известный парадокс сингулярной теории упругости в линейной механике разрушения: напряжения в вершине трещины обращаются в бесконечность, но особенность (1/2) оказывается интегрируемой, что приводит к конечному значению энергии, высвобождаемой при росте трещины. Так и в данном случае: прогиб (формально) обращается в бесконечность, но упругая энергия, равная работе распределенной нагрузки на этом прогибе, оказывается конечной. Массовая эффективность (21) становится одинаковой для различных равнопрочных балок, как и в (14), т.е. при заданной накопленной упругой энергии масса равномерно нагруженных равнопрочных балок в пять раз меньше, чем прямоугольных с той же прочностью.
3. Вид III – линейно меняющаяся нагрузка (тройной штрих) (рис. 1, III).
Линейно распределенная нагрузка: $p(x)$ = ${{p}_{{{\text{max}}}}}(1 - x{\text{/}}l)$ = ${{p}_{{{\text{max}}}}}z$ приводит к переменному изгибающему моменту: $M(x)$ = ${{p}_{{{\text{max}}}}}{{l}^{2}}{{z}^{3}}{\text{/}}6$ = ${{P}_{{{\text{max}}}}}l{{z}^{3}}{\text{/}}3$. Условие прочности (15) примет вид
а условие равнопрочности (16)(23)
$\frac{{{{p}_{{{\text{max}}}}}{{{(l - x)}}^{3}}}}{{{{w}_{i}}(x)t_{i}^{2}(x)}} = \frac{{{{p}_{{{\text{max}}}}}{{l}^{3}}}}{{{{w}_{i}}(0)t_{i}^{2}(0)}} \Rightarrow {{\alpha }_{i}} + 2{{\beta }_{i}} = 3.$Попытка вычисления максимального прогиба двойным интегрированием уравнения типа (17) снова приводит к расходящимся интегралам, так как точки, соответствующие балкам с приведенными в табл. 3 значениями ${{\alpha }_{i}}$; ${{\beta }_{i}}$, лежат вне допустимого сектора на рис. 4. Однако интеграл от произведения переменного прогиба на переменную нагрузку дает конечные значения накопленной энергии изгиба равнопрочной балки. Отношения $\delta _{{Ui}}^{{{\text{''}}}}$ этой энергии к энергии изгиба прямоугольной балки приведены в табл. 3. Для переменной нагрузки, мы получим коэффициент снижения массы для равнопрочной балки $({{\alpha }_{i}} = 3 - 2{{\beta }_{i}})$ под действием линейно меняющейся нагрузки
(24)
$\delta _{{Si}}^{{{\text{'''}}}} = \frac{{\delta _{{mi}}^{{{\text{'''}}}}}}{{\delta _{{Ui}}^{{{\text{'''}}}}}} = \frac{{7 - {{\alpha }_{i}} - 3{{\beta }_{i}}}}{{7(1 + {{\alpha }_{i}} + {{\beta }_{i}})}} = \frac{{4 - \beta }}{{7(4 - \beta )}} = \frac{1}{7}.$Таблица 3.
Параметры консольных балок, равнопрочных под действием линейно меняющейся распределенной нагрузки (вид III)
| i | Тип балки: | ${{\alpha }_{i}}$ | ${{\beta }_{i}}$ | $\delta _{{{v}i}}^{{'''}}$ | $\delta _{{mi}}^{{'''}}$ | $\delta _{{Ui}}^{{'''}}$ | $\delta _{{Si}}^{{{\text{'''}}}}$ |
|---|---|---|---|---|---|---|---|
| 1 | $t(x) = {\text{const}}$ | 3 | 0 | ∞ | 1/4 | 7/4 | 1/7 |
| 2 | $w(x) = {\text{const}}$ | 0 | 3/2 | ∞ | 2/5 | 14/5 | 1/7 |
| 3 | $w(x)t(x) = {\text{const}}$ | –3 | 3 | ∞ | 1 | 7 | 1/7 |
Из (14), (21), (24) видно, что чем более неравномерно меняется изгибающий момент, тем больший эффект дает равнопрочное профилирование.
4. Оценка области корректности балочного приближения. Случай концевой силы кажется совершенно простым и изученным, но даже для этого случая не все “равнопрочные” проекты могут быть исследованы в балочном приближении. На рис. 4 приведена графическая иллюстрация области допустимых проектов. Начало координат (0 в кружке) соответствует прямоугольной балке. Прямая 5, построенная по уравнению (5), соответствует множеству равнопрочных проектов: на осях – цифры 1 и 2 в кружках соответствуют традиционным треугольной и параболической балкам. Прямые 6, 7 и другие с тем же наклоном определяют проекты равной массы. Прямая 6 соответствует балкам констэра с той же массой, что и у прямоугольной балки. Пересечение прямых 6 и 5 (3 в кружке) – это констэра, равнопрочная при действии концевой силы. Чем ниже прямые типа 6, тем балка тяжелее, но ниже прямой 7 проектов нет, т.к. их масса обращается в бесконечность. Пересечение прямых 7 и 5 в т. С (–3; 2) определяет “бесконечно тяжелую”, но равнопрочную балку. Прямые типа 1 соответствуют проектам с одинаковым коэффициентом формы по прогибу. Чем ниже подобные прямые, тем балка жестче. Прямая 1, проходящая через точки 3 и 1 на осях, ограничивает область допустимых проектов сверху. На ней прогиб обращается в бесконечность. Таким образом, прямые 1 и 7 ограничивают сектор допустимых проектов с вершиной в точке С (–3; 2). Вне этого сектора балочное приближение приводит к расходящимся интегралам. Например, для констэры (прямая 6) точки В с координатами $\alpha _{3}^{{{\text{''}}}} = - 2$; $\beta _{3}^{{{\text{''}}}} = 2$ и D с координатами $\alpha _{3}^{{{\text{'''}}}}$ = $ - \beta _{3}^{{{\text{'''}}}}$ = –3 выходят за пределы допустимого сектора на рис. 4, поэтому расчет их максимального прогиба становится некорректным.
5. Применение энергетического подхода. Приведенные выше иллюстрации могут быть легко обобщены с использованием теоремы Кастильяно, согласно которой можно оценить накопленную упругую энергию в балке с переменным сечением под действием изменяющегося по длине момента
(25)
${{U}_{{\text{*}}}} = \frac{6}{E}\int\limits_0^l {\frac{{{{M}^{2}}(x)}}{{w(x){{t}^{3}}(x)}}dx.} $Рассмотрим общий случай степенного изменения изгибающего момента
Вспомним, что перерезывающая сила выражается в виде производной от момента, а распределенная нагрузка – в виде производной от перерезывающей силы: P(x) = = $dM{\text{/}}dx$; $p(x) = dP{\text{/}}dx$, поэтому рассмотренный выше вид I соответствует $\gamma = 1$, вид II – $\gamma = 2$ вид III – $\gamma = 3$.
Из заданных прочности и упругой энергии найдем требуемые размеры сечения прямоугольной балки $\alpha = \beta = 0$.
(27)
$\begin{gathered} {\text{1)}}{\text{.}}\;{{\sigma }_{{\text{*}}}} = \frac{{6{{M}_{0}}}}{{w_{0}^{{}}t_{0}^{2}}}{\text{;}}\quad {\text{2)}}{\text{.}}\;{{U}_{{\text{*}}}} = \frac{{6M_{0}^{2}l}}{{E{{w}_{0}}t_{0}^{3}}}\int\limits_0^1 {{{z}^{{2\gamma }}}dz = } \frac{{6M_{0}^{2}l}}{{E{{w}_{0}}t_{0}^{3}}}\frac{1}{{1 + 2\gamma }}{\text{;}} \\ {\text{Из}}\;{\text{1)}}{\text{.}}{\kern 1pt} - {\kern 1pt} {\text{2)}}{\text{.}} \Rightarrow {{t}_{0}} = \frac{{{{\sigma }_{{\text{*}}}}{{M}_{0}}l}}{{{{U}_{{\text{*}}}}E}}\frac{1}{{1 + 2\gamma }}{\text{;}}\quad {{w}_{0}} = \frac{{6U_{{\text{*}}}^{2}{{E}^{2}}{{{(1 + 2\gamma )}}^{2}}}}{{\sigma _{{\text{*}}}^{3}{{M}_{0}}{{l}^{2}}}} \Rightarrow \\ {{m}_{0}} = \rho {{w}_{0}}{{t}_{0}}l = \frac{{6\rho {{U}_{{\text{*}}}}E}}{{\sigma _{{\text{*}}}^{2}}}(1 + 2\gamma ). \\ \end{gathered} $Для профилированной равнопрочной балки: $w(x) = w(0){{z}^{\alpha }}$; $t(x) = t(0){{z}^{\beta }}$, удовлетворяющей тем же условиям по прочности и запасенной энергии, что и прямоугольная, рассмотренная выше балка
(28)
$\begin{gathered} {\text{из}}\;{\text{1)}}{\text{.}}{\kern 1pt} - {\kern 1pt} {\text{2)}}{\text{.}} \Rightarrow t(0) = \frac{{{{\sigma }_{{\text{*}}}}{{M}_{0}}l}}{{{{U}_{{\text{*}}}}E(1 + 2\gamma - \alpha - 3\beta )}} = {{t}_{0}}{{\delta }_{U}}{\text{;}} \\ w(0) = \frac{{6U_{{\text{*}}}^{2}{{E}^{2}}{{{(1 + 2\gamma - \alpha - 3\beta )}}^{2}}}}{{\sigma _{{\text{*}}}^{3}{{M}_{0}}{{l}^{2}}}} = {{w}_{0}}\delta _{U}^{2} \Rightarrow m = \rho w(0)t(0)l{{\delta }_{m}} = \rho {{w}_{0}}{{t}_{0}}l\frac{{{{\delta }_{m}}}}{{{{\delta }_{U}}}} = {{m}_{0}}{{\delta }_{S}}. \\ \end{gathered} $Учитывая, что ${{\delta }_{m}} = \frac{1}{{1 + \alpha + \beta }}$; ${{\delta }_{U}} = \frac{{1 + 2\gamma }}{{1 + 2\gamma - \alpha - 3\beta }}$, находим из условия равнопрочности
(29)
$\begin{gathered} \frac{{{{M}_{0}}{{z}^{\gamma }}}}{{w(x){{t}^{2}}(x)}} = \frac{{6{{M}_{0}}}}{{w(0){{t}^{2}}(0)}} = {\text{const}} \Rightarrow \alpha + 2\beta = \gamma \Rightarrow \\ \Rightarrow {{\delta }_{S}} = \frac{{{{\delta }_{m}}}}{{{{\delta }_{U}}}} = \frac{{1 + 2\gamma - \alpha - 3\beta }}{{(1 + 2\gamma )(1 + \alpha + \beta )}} = ({\text{из}}\;\alpha = \gamma - 2\beta ) = \frac{{1 + 2\gamma - \gamma - \beta }}{{(1 + 2\gamma )(1 + \gamma - \beta )}} = \frac{1}{{1 + 2\gamma }}. \\ \end{gathered} $Результат (29) обобщает и объясняет одинаковые значения коэффициентов снижения массы, показанные в табл. 1–3, для разных типов равнопрочных балок.
Выводы. 1) равнопрочные балки при заданных прочности и накопленной упругой энергии дают по сравнению с прямоугольным трехкратное снижение массы при нагружении концевой силой и пятикратное при равномерно распределенной нагрузке. Для изменения изгибающего момента по произвольному степенному закону M(x) ~ ~ (1 ‒ $x{\text{/}}l{{)}^{\gamma }}$ коэффициент снижения массы выражается простой формулой ${{\delta }_{S}} = {{(1 + 2\gamma )}^{{ - 1}}}$; 2) существуют границы применимости линейных моделей при расчете прогибов профилированных композитных балок. Балочное приближение приводит к некорректным результатам для равнопрочных балок с достаточно быстрым изменением размеров. Это еще одно, не общеизвестное, ограничение в дополнение к традиционным требованиям малых прогибов и малых углов поворота сечений; 3) вычисление накопленной упругой энергии корректно даже для случаев, когда прогибы (формально) выражаются расходящимися интегралами.
Список литературы
Черепанов Г.П. Равнопрочный тяжелый брус: решение проблемы Галилея // Физическая мезомеханика. 2016. Т. 19. № 1. С. 84.
Polilov A.N., Tatus N.A., Shabalin V.V. Peculiarities of constructing elastic elements in the form of shaped composite beams // J. of Machinery Manufacture and Reliability. 2011. V. 40. № 6. P. 532.
Няшин Ю.И., Осипенко М.А., Гитман М.Б. Равнонапряженные листовые рессоры // Вестник Магнитогорского государственного технического университета им. Г.И. Носова. 2014. № 4 (48). С. 22.
Polilov A.N., Tatus N.A., Plitov I.S. Estimating the effect of misorientation of fibers on stiffness and strength of profiled composite elements // Journal of Machinery Manufacture and Reliability. 2013. V. 42. № 5. P. 390.
Wegst U.G.K., Ashby M.F. The structural efficiency of orthotropic stalks, stems and tubes // Journal of Material Science. 2007. V. 42. P. 9005.
Gordon J.E. The New Science of Strong Materials Or Why You Don’t Fall through the Floor – Princeton university press. 2018. P. 328.
Eloy C., Fournier M., Lacointe A., Moulia B. Wind loads and competition for light sculpt trees into self-similar structures // Nat. Commun. 2017. № 8. P. 1014.
Осипенко М.А., Няшин Ю.И. Об оптимизации упругого элемента протеза стопы // Российский журнал биомеханики. 2011. Т. 15. № 2. С. 16.
Полилов А.Н., Татусь Н.А. Биомеханика прочности волокнистых композитов. М.: ФИЗМАТЛИТ. 2018. С. 328.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин