1. На главную
  2. Электронные версии
  3. Проблемы машиностроения и надежности машин
  4. № 5, 2019

Проблемы машиностроения и надежности машин, 2019, № 5, стр. 18-26

К РЕШЕНИЮ ПРЯМОЙ ЗАДАЧИ О ПОЛОЖЕНИЯХ l-КООРДИНАТНЫХ МЕХАНИЗМОВ РАЗЛИЧНОГО ТИПА

Г. В. Рашоян 1, С. М. Демидов 1, *, А. К. Алешин 1, А. В. Антонов 1, С. А. Скворцов 1, К. А. Шалюхин 1

1 Институт машиноведения имени А.А. Благонравова РАН
г. Москва, Россия

* E-mail: chipd@rambler.ru

Поступила в редакцию 06.03.2019
Принята к публикации 25.06.2019

Полный текст (PDF)

Аннотация

В статье рассматривается алгоритм решения прямой задачи о положениях для пространственных механизмов параллельной структуры с шестью линейными приводами. В зависимости от структурной схемы l-координатного механизма прямая задача решается как аналитически, так и итерационно-численно. В основе аналитического решения лежит математическая модель из системы трех уравнений прямых, проходящих через одну точку. Решена задача перехода от координат точек выходного звена механизма к его абсолютным координатам. Приведен пример решения задачи.

Ключевые слова: механизм параллельной структуры, l-координатный механизм, задача о положениях

Известно, что аналитическое решение задачи о положениях является эффективным средством для описания рабочей зоны выходного звена механизмов параллельной структуры, исследования траектории движения промежуточных звеньев, для оценки функциональных возможностей, а также наличия особых положений [1–12].

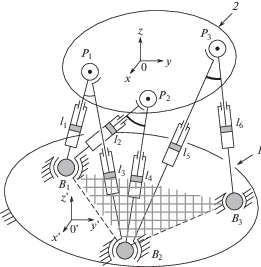
Одним из видов механизмов параллельной структуры являются l-координатные механизмы (рис. 1), состоящие из шести соединительных цепей с одной поступательной приводной парой и двумя сферическими неприводными парами, соединенными с основанием 1 и выходным звеном 2. Известно, что аналитический алгоритм решения прямой задачи о положениях имеет место лишь для некоторых l-координатных структурных схем.

Рис. 1.

l-координатный механизм, соответствующий аналитическому решению прямой задачи о положениях.

Пусть заданы координаты точек ${{B}_{j}}(X_{{Bj}}^{{\text{'}}},~Y_{{Bj}}^{{\text{'}}},~Z_{{Bj}}^{{\text{'}}})$ ( j = 1, 2, 3) в неподвижной системе координат $O{\text{'}}X{\text{'}}Y{\text{'}}Z{\text{'}}$, связанной с основанием 1, и координаты точек ${{P}_{i}}({{X}_{{Pi}}},~{{Y}_{{Pi}}},~{{Z}_{{Pi}}})$ (i = 1, 2, 3) в подвижной системе координат $OXYZ$, связанной с выходным звеном 2 механизма. Известны значения l-координат l1, …, l6, длины отрезков на выходном звене: lP1P2, lP2P3, lP1P3, длины отрезков на основании: lB1B2, lB2B3, lB1B3. Необходимо определить положение выходного звена 2 в неподвижной системе координат $O{\text{'}}X{\text{'}}Y{\text{'}}Z{\text{'}}$.

Очевидно, что определение положения выходного звена эквивалентно определению координат точек Pi в неподвижной системе координат $O{\text{'}}X{\text{'}}Y{\text{'}}Z{\text{'}}$, где i = 1, 2, 3. Сначала определим положение точки B2 в системе координат выходного звена механизма [12]. Составим систему уравнений

(1)
$\left\{ {\begin{array}{*{20}{c}} {{{{({{X}_{{P1}}} - {{X}_{{B2}}})}}^{2}} + {{{({{Y}_{{P1}}} - {{Y}_{{B2}}})}}^{2}} + {{{({{Z}_{{P1}}} - {{Z}_{{B2}}})}}^{2}} = l_{3}^{2},} \\ {{{{({{X}_{{P2}}} - {{X}_{{B2}}})}}^{2}} + {{{({{Y}_{{P2}}} - {{Y}_{{B2}}})}}^{2}} + {{{({{Z}_{{P2}}} - {{Z}_{{B2}}})}}^{2}} = l_{4}^{2},} \\ {{{{({{X}_{{P3}}} - {{X}_{{B2}}})}}^{2}} + {{{({{Y}_{{P3}}} - {{Y}_{{B2}}})}}^{2}} + {{{({{Z}_{{P3}}} - {{Z}_{{B2}}})}}^{2}} = l_{5}^{2}.} \end{array}} \right.$

На примере системы (1) покажем алгоритм решения системы квадратных уравнений, идея метода ранее была предложена К.С. Арзуманяном и А.Ш. Колискором. Для этого раскроем скобки во всех трех уравнениях системы и вычтем из первого второе и третье уравнения, получим следующие соотношения

(2)
${{X}_{{B2}}}({{X}_{{P2}}} - {{X}_{{P1}}}) + {{Y}_{{B2}}}({{Y}_{{P2}}} - {{Y}_{{P1}}}) + {{Z}_{{B2}}}({{Z}_{{P2}}} - {{Z}_{{P1}}}) = {{t}_{1}},$
(3)
${{X}_{{B2}}}({{X}_{{P3}}} - {{X}_{{P1}}}) + {{Y}_{{B2}}}({{Y}_{{P3}}} - {{Y}_{{P1}}}) + {{Z}_{{B2}}}({{Z}_{{P3}}} - {{Z}_{{P1}}}) = {{t}_{2}},$
где:

${{t}_{1}} = \frac{{l_{3}^{2} - l_{4}^{2} - {{K}_{1}} + {{K}_{2}}}}{2},$
${{t}_{2}} = \frac{{l_{3}^{2} - l_{5}^{2} - {{K}_{1}} + {{K}_{3}}}}{2},$
${{K}_{1}} = X_{{P1}}^{2} + Y_{{P1}}^{2} + Z_{{P1}}^{2},$
${{K}_{2}} = X_{{P2}}^{2} + Y_{{P2}}^{2} + Z_{{P2}}^{2},$
${{K}_{3}} = X_{{P3}}^{2} + Y_{{P3}}^{2} + Z_{{P3}}^{2}.$

Решим уравнения (2) и (3) относительно переменных ${{Y}_{{B2}}}$ и ${{X}_{{B2}}}$, выражая их через координату ${{Z}_{{B2}}}$, при этом получим:

(4)
${{Y}_{{B2}}} = {{K}_{4}} + {{K}_{5}}{{Z}_{{B2}}},$
(5)
${{X}_{{B2}}} = {{K}_{6}} + {{K}_{7}}{{Z}_{{B2}}},$
где:

${{K}_{4}} = \frac{{t2({{X}_{{P2}}} - {{X}_{{P1}}}) - t1({{X}_{{P3}}} - {{X}_{{P1}}})}}{{({{X}_{{P2}}} - {{X}_{{P1}}})({{Y}_{{P3}}} - {{Y}_{{P1}}}) - ({{Y}_{{P2}}} - {{Y}_{{P1}}})({{X}_{{P3}}} - {{X}_{{P1}}})}}{\text{\;}},$
${{K}_{5}} = \frac{{({{Z}_{{P2}}} - {{Z}_{{P1}}})({{X}_{{P3}}} - {{X}_{{P1}}}) - ({{Z}_{{P3}}} - {{Z}_{{P1}}})({{X}_{{P2}}} - {{X}_{{P1}}})}}{{({{X}_{{P2}}} - {{X}_{{P1}}})({{Y}_{{P3}}} - {{Y}_{{P1}}}) - ({{Y}_{{P2}}} - {{Y}_{{P1}}})({{X}_{{P3}}} - {{X}_{{P1}}})}},$
${{K}_{6}} = \frac{{t2~({{Y}_{{P2}}} - {{Y}_{{P1}}}) - t1({{Y}_{{P3}}} - {{Y}_{{P1}}})}}{{({{X}_{{P3}}} - {{X}_{{P1}}})({{Y}_{{P2}}} - {{Y}_{{P1}}}) - ({{X}_{{P2}}} - {{X}_{{P1}}})({{Y}_{{P3}}} - {{Y}_{{P1}}})}},$
${{K}_{7}} = \frac{{({{Z}_{{P2}}} - {{Z}_{{P1}}})({{Y}_{{P3}}} - {{Y}_{{P1}}}) - ({{Z}_{{P3}}} - {{Z}_{{P1}}})({{Y}_{{P2}}} - {{Y}_{{P1}}})}}{{({{X}_{{P3}}} - {{X}_{{P1}}})({{Y}_{{P2}}} - {{Y}_{{P1}}}) - ({{X}_{{P2}}} - {{X}_{{P1}}})({{Y}_{{P3}}} - {{Y}_{{P1}}})}}.$

Подставляя (4) и (5) в первое уравнение системы (1), получим квадратное уравнение относительно переменной ${{Z}_{{B2}}}$

(6)
${{a}_{1}}Z_{{B2}}^{2} + {{a}_{2}}{{Z}_{{B2}}} + {{a}_{3}} = 0,$
где:

${{a}_{1}} = K_{5}^{2} + K_{7}^{2} + 1,$
${{a}_{2}} = 2( - {{X}_{{P1}}}{{K}_{7}} + {{K}_{4}}{{K}_{5}} - {{Y}_{{P1}}}{{K}_{5}} + {{K}_{6}}{{K}_{7}} - {{Z}_{{P1}}}),$
${{a}_{3}} = {{K}_{1}} + K_{4}^{2} + K_{6}^{2} - 2{{X}_{{P1}}}{{K}_{6}} - 2{{Y}_{{P1}}}{{K}_{4}} - l_{3}^{2}.$

Уравнение (6) имеет решение, корни которого принимают следующий вид:

(7)
${{Z}_{{B2}}} = \frac{{ - {{a}_{2}} \pm \sqrt {a_{2}^{2} - 4{{a}_{1}}{{a}_{3}}} }}{{2{{a}_{1}}}}.$

Необходимо отметить, что выражение (7) имеет неоднозначное решение, связанное со знаком перед квадратным корнем. Для исключения неоднозначности предлагается рассматривать одну сборку механизма. Подставив в уравнения (4) и (5) полученный результат (7), получим остальные координаты точки ${{B}_{2}}$.

Для определения координат точек B1 и B3 составим две системы уравнений, алгоритм решения, которых аналогичен (1):

$\left\{ {\begin{array}{*{20}{l}} {{{{({{X}_{{P1}}} - {{X}_{{B1}}})}}^{2}} + {{{({{Y}_{{P1}}} - {{Y}_{{B1}}})}}^{2}} + {{{({{Z}_{{P1}}} - {{Z}_{{B1}}})}}^{2}} = l_{1}^{2},} \\ {{{{({{X}_{{P2}}} - {{X}_{{B1}}})}}^{2}} + {{{({{Y}_{{P2}}} - {{Y}_{{B1}}})}}^{2}} + {{{({{Z}_{{P2}}} - {{Z}_{{B1}}})}}^{2}} = l_{2}^{2},} \\ {{{{({{X}_{{B2}}} - {{X}_{{B1}}})}}^{2}} + {{{({{Y}_{{B2}}} - {{Y}_{{B1}}})}}^{2}} + {{{({{Z}_{{B2}}} - {{Z}_{{B1}}})}}^{2}} = l_{{B2B1}}^{2},} \end{array}} \right.$
$\left\{ {\begin{array}{*{20}{l}} {{{{({{X}_{{P3}}} - {{X}_{{B3}}})}}^{2}} + {{{({{Y}_{{P3}}} - {{Y}_{{B3}}})}}^{2}} + {{{({{Z}_{{P3}}} - {{Z}_{{B3}}})}}^{2}} = l_{6}^{2},} \\ {{{{({{X}_{{B1}}} - {{X}_{{B3}}})}}^{2}} + {{{({{Y}_{{B1}}} - {{Y}_{{B3}}})}}^{2}} + {{{({{Z}_{{B1}}} - {{Z}_{{B3}}})}}^{2}} = l_{{B1B3}}^{2},} \\ {{{{({{X}_{{B2}}} - {{X}_{{B3}}})}}^{2}} + {{{({{Y}_{{B2}}} - {{Y}_{{B3}}})}}^{2}} + {{{({{Z}_{{B2}}} - {{Z}_{{B3}}})}}^{2}} = l_{{B2B3}}^{2}.} \end{array}} \right.$

Затем, имея координаты точек Pi (i = 1, 2, 3) в подвижной системе координат, можно рассчитать длины дополнительных отрезков lP1B3, lP2B3, lP3B1. Это позволит подобно (1) определить координаты точек Pi в неподвижной системе координат. Таким образом, прямая задача о положениях решена.

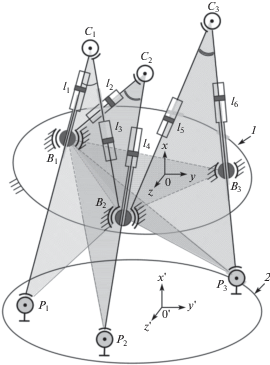
Далее рассмотрим решение прямой задачи о положениях для l-координатного механизма, полученного из исходного [6] путем переноса выходного звена в область вне расположения приводов (рис. 2). Задача, как и ранее, сводится к определению положения выходного звена 2 механизма по заданным значениям l-координат.

Рис. 2.

Механизм с приводами, расположенными вне рабочей зоны.

Считаем заданными положения точек ${{B}_{j}}({{X}_{{Bj}}},{{Y}_{{Bj}}},{{Z}_{{Bj}}})$ ( j = 1, 2, 3) в неподвижной системе координат $OXYZ$, связанной с основанием 1, а также координаты точек ${{P}_{i}}(X_{{Pi}}^{{\text{'}}},Y_{{Pi}}^{{\text{'}}},Z_{{Pi}}^{{\text{'}}})$ (i = 1, 2, 3) в подвижной системе координат $O{\text{'}}X{\text{'}}Y{\text{'}}Z{\text{'}}$, связанной с выходным звеном 2 механизма. Кроме того, известны значения l-координат l1, …, l6, длины отрезков на выходном звене lP1P2, lP2P3, lP1P3, длины отрезков на основании lB1B2, lB2B3, lB1B3, а также длины штанг lP1C2, lP2C3, lP1C3. Необходимо определить положение выходного звена 2 в неподвижной системе координат $OXYZ$, что эквивалентно определению координат точек ${{P}_{i}}({{X}_{{Pi}}},~{{Y}_{{Pi}}},~{{Z}_{{Pi}}})$ в неподвижной системе координат $OXYZ$, связанной с основанием 1, где i = 1, 2, 3.

Для решения поставленной задачи рассмотрим треугольник $\vartriangle $B2C3B3. Согласно теореме косинусов, длины отрезков l5, l6, lB2B3, соответствующих сторонам данного треугольника, связаны следующим выражением:

$l_{5}^{2} + l_{6}^{2} - 2{{l}_{5}}{{l}_{6}}\cos \angle {{B}_{2}}{{C}_{3}}{{B}_{3}} = l_{{B2B3}}^{2},$
откуда определим косинус угла:

$\cos \angle {{B}_{2}}{{C}_{3}}{{B}_{3}} = \frac{{l_{5}^{2} + l_{6}^{2} - l_{{B2B3}}^{2}}}{{2{{l}_{5}}{{l}_{6}}}}.$

Далее из треугольника $\vartriangle $B2C3P3 находим длину отрезка lP3B2:

(8)
${{l}_{{P3B2}}} = \sqrt {l_{5}^{2} + l_{6}^{2} - 2{{l}_{5}}{{l}_{6}}\cos \angle {{B}_{2}}{{C}_{3}}{{B}_{3}}} .$

Аналогичным образом, рассматривая треугольники $\vartriangle $B2C1P1 и $\vartriangle $B1C2P2, подобно уравнению (8), находим длины отрезков lP1B2 и lP2B1

(9)
$\begin{gathered} {{l}_{{P1B2}}} = \sqrt {l_{{P1C1}}^{2} + l_{3}^{2} - 2{{l}_{{P1C1}}}{{l}_{3}}\cos \angle {{P}_{1}}{{C}_{1}}{{B}_{2}}} , \\ {{l}_{{P2B1}}} = \sqrt {l_{2}^{2} + l_{{P2C2}}^{2} - 2{{l}_{2}}{{l}_{{P2C2}}}\cos \angle {{B}_{1}}{{C}_{2}}{{B}_{2}}} . \\ \end{gathered} $

Далее в подвижной системе координат $O{\text{'}}X{\text{'}}Y{\text{'}}Z{\text{'}}$ определяем положение точки ${{B}_{2}}(X_{{B2}}^{{\text{'}}},Y_{{B2}}^{{\text{'}}},Z_{{B2}}^{{\text{'}}})$. Для этого составим систему из квадратных уравнений, связывающих координаты искомой точки ${{B}_{2}}$ с координатами точек ${{P}_{1}}$, ${{P}_{2}}$, ${{P}_{3}}$

$\left\{ {\begin{array}{*{20}{c}} {{{{(X_{{P1}}^{{\text{'}}} - X_{{B2}}^{{\text{'}}})}}^{2}} + {{{(Y_{{P1}}^{{\text{'}}} - Y_{{B2}}^{{\text{'}}})}}^{2}} + {{{(Z_{{P1}}^{{\text{'}}} - Z_{{B2}}^{{\text{'}}})}}^{2}} = l_{{P1B2}}^{2},} \\ {{{{(X_{{P2}}^{{\text{'}}} - X_{{B2}}^{{\text{'}}})}}^{2}} + {{{(Y_{{P2}}^{{\text{'}}} - Y_{{B2}}^{{\text{'}}})}}^{2}} + {{{(Z_{{P2}}^{{\text{'}}} - Z_{{B2}}^{{\text{'}}})}}^{2}} = l_{{P2B2}}^{2},} \\ {{{{(X_{{P3}}^{{\text{'}}} - X_{{B2}}^{{\text{'}}})}}^{2}} + {{{(Y_{{P3}}^{{\text{'}}} - Y_{{B2}}^{{\text{'}}})}}^{2}} + {{{(Z_{{P3}}^{{\text{'}}} - Z_{{B2}}^{{\text{'}}})}}^{2}} = l_{{P3B2}}^{2},} \end{array}} \right.$
в которой значения длин отрезков $~{{l}_{{P1B2}}}$ и ${{l}_{{P3B2}}}$ соответствуют выражениям (8) и (9). Определим длину отрезка ${{l}_{{P2B2}}} = {{l}_{{P2С2}}} - {{l}_{4}}$, в котором длина ${{l}_{{P2С2}}}$ также является заданной.

Далее определим координаты точки ${{C}_{2}}(X_{{C2}}^{{\text{'}}},Y_{{C2}}^{{\text{'}}},Z_{{C2}}^{{\text{'}}})$ в подвижной системе координат. Для этого сначала составим уравнение прямой, проходящей через две заданные точки ${{P}_{2}}(X_{{P2}}^{{\text{'}}},Y_{{P2}}^{{\text{'}}},Z_{{P2}}^{{\text{'}}})$ и ${{B}_{2}}(X_{{B2}}^{{\text{'}}},Y_{{B2}}^{{\text{'}}},Z_{{B2}}^{{\text{'}}})$

(10)
$\frac{{X - X_{{P2}}^{{\text{'}}}}}{{X_{{B2}}^{{\text{'}}} - X_{{P2}}^{{\text{'}}}}} = \frac{{Y - Y_{{P2}}^{{\text{'}}}}}{{Y_{{B2}}^{{\text{'}}} - Y_{{P2}}^{{\text{'}}}}} = \frac{{Z - Z_{{P2}}^{{\text{'}}}}}{{Z_{{B2}}^{{\text{'}}} - Z_{{P2}}^{{\text{'}}}}}.$

Затем по заданным длинам отрезков ${{l}_{{P2С2}}}$ и ${{l}_{{P2B2}}}$ определим координаты точки ${{C}_{2}}(X_{{C2}}^{{\text{'}}},Y_{{C2}}^{{\text{'}}},Z_{{C2}}^{{\text{'}}})$, лежащей на прямой, заданной уравнением (10). Для этого составим уравнения

$\frac{{X_{{C2}}^{{\text{'}}} - X_{{P2}}^{{\text{'}}}}}{{X_{{B2}}^{{\text{'}}} - X_{{P2}}^{{\text{'}}}}} = \frac{{{{l}_{{P2С2}}}}}{{{{l}_{{P2B2}}}}},\quad \frac{{Y_{{C2}}^{{\text{'}}} - Y_{{P2}}^{{\text{'}}}}}{{Y_{{B2}}^{{\text{'}}} - Y_{{P2}}^{{\text{'}}}}} = \frac{{{{l}_{{P2С2}}}}}{{{{l}_{{P2B2}}}}},\quad \frac{{Z_{{C2}}^{{\text{'}}} - Z_{{P2}}^{{\text{'}}}}}{{Z_{{B2}}^{{\text{'}}} - Z_{{P2}}^{{\text{'}}}}} = \frac{{{{l}_{{P2С2}}}}}{{{{l}_{{P2B2}}}}},$
из которых находим координаты $X_{{C2}}^{{\text{'}}},Y_{{C2}}^{{\text{'}}},Z_{{C2}}^{{\text{'}}}$.

Определим положение точки ${{B}_{1}}(X_{{B1}}^{{\text{'}}},Y_{{B1}}^{{\text{'}}},Z_{{B1}}^{{\text{'}}})$ в подвижной системе координат $O{\text{'}}X{\text{'}}Y{\text{'}}Z{\text{'}}$. Для этого составим систему из квадратных уравнений связывающие координаты искомой точки ${{B}_{1}}$ с координатами точек ${{P}_{1}}$, ${{C}_{2}}$, ${{P}_{2}}$

$\left\{ {\begin{array}{*{20}{l}} {{{{(X_{{B1}}^{{\text{'}}} - X_{{P1}}^{{\text{'}}})}}^{2}} + {{{(Y_{{B1}}^{{\text{'}}} - Y_{{P1}}^{{\text{'}}})}}^{2}} + {{{(Z_{{B1}}^{{\text{'}}} - Z_{{P1}}^{{\text{'}}})}}^{2}} = l_{{P1B1}}^{2},} \\ {{{{(X_{{B1}}^{{\text{'}}} - X_{{C2}}^{{\text{'}}})}}^{2}} + {{{(Y_{{B1}}^{{\text{'}}} - Y_{{C2}}^{{\text{'}}})}}^{2}} + {{{(Z_{{B1}}^{{\text{'}}} - Z_{{C2}}^{{\text{'}}})}}^{2}} = l_{2}^{2},} \\ {{{{(X_{{B1}}^{{\text{'}}} - X_{{P2}}^{{\text{'}}})}}^{2}} + {{{(Y_{{B1}}^{{\text{'}}} - Y_{{P2}}^{{\text{'}}})}}^{2}} + {{{(Z_{{B1}}^{{\text{'}}} - Z_{{P2}}^{{\text{'}}})}}^{2}} = l_{{P2B1}}^{2},} \end{array}} \right.$
где ${{l}_{{P1B1}}} = {{l}_{{P1С1}}} - {{l}_{1}}$.

Далее в подвижной системе координат рассмотрим тетраэдр ${{B}_{1}}{{B}_{2}}{{P}_{3}}{{B}_{3}}$ с вершиной в точке ${{B}_{3}}$ и составим систему квадратных уравнений, связывающих координаты точек основания тетраэдра ${{B}_{1}}$, ${{B}_{2}}$, ${{P}_{3}}$ с координатами его вершины в точке ${{B}_{3}}$, при этом получим

$\left\{ {\begin{array}{*{20}{l}} {{{{(X_{{B3}}^{{\text{'}}} - X_{{B1}}^{{\text{'}}})}}^{2}} + {{{(Y_{{B3}}^{{\text{'}}} - Y_{{B1}}^{{\text{'}}})}}^{2}} + {{{(Z_{{B3}}^{{\text{'}}} - Z_{{B1}}^{{\text{'}}})}}^{2}} = l_{{B1B3}}^{2},} \\ {{{{(X_{{B3}}^{{\text{'}}} - X_{{B2}}^{{\text{'}}})}}^{2}} + {{{(Y_{{B3}}^{{\text{'}}} - Y_{{B2}}^{{\text{'}}})}}^{2}} + {{{(Z_{{B3}}^{{\text{'}}} - Z_{{B2}}^{{\text{'}}})}}^{2}} = l_{{B2B3}}^{2},} \\ {{{{(X_{{B3}}^{{\text{'}}} - X_{{P3}}^{{\text{'}}})}}^{2}} + {{{(Y_{{B3}}^{{\text{'}}} - Y_{{P3}}^{{\text{'}}})}}^{2}} + {{{(Z_{{B3}}^{{\text{'}}} - Z_{{P3}}^{{\text{'}}})}}^{2}} = l_{{P3B3}}^{2}.} \end{array}} \right.$

Длину отрезка ${{l}_{{P3B3}}}$ определим из соотношения:

${{l}_{{P3B3}}} = {{l}_{{P3С3}}} - {{l}_{6}},$
при этом длина ${{l}_{{P3С3}}}$ также является заданной.

Имея координаты точек ${{B}_{1}}$, ${{B}_{2}}$, ${{B}_{3}}$ в подвижной системе координат, можно определить расстояние между любыми точками ${{B}_{1}}$, ${{B}_{2}}$, ${{B}_{3}}$, ${{P}_{1}}$, ${{P}_{2}}$, ${{P}_{3}}$, в подвижной системе координат. В частности, определим длины следующих отрезков

${{l}_{{P1B3}}} = \sqrt {{{{(X_{{P1}}^{{\text{'}}} - X_{{B3}}^{{\text{'}}})}}^{2}} + {{{(Y_{{P1}}^{{\text{'}}} - Y_{{B3}}^{{\text{'}}})}}^{2}} + {{{(Z_{{P1}}^{{\text{'}}} - Z_{{B3}}^{{\text{'}}})}}^{2}}} ,$
${{l}_{{P2B3}}} = \sqrt {{{{(X_{{P2}}^{{\text{'}}} - X_{{B3}}^{{\text{'}}})}}^{2}} + {{{(Y_{{P2}}^{{\text{'}}} - Y_{{B3}}^{{\text{'}}})}}^{2}} + {{{(Z_{{P2}}^{{\text{'}}} - Z_{{B3}}^{{\text{'}}})}}^{2}},} $
${{l}_{{P3B1}}} = \sqrt {{{{(X_{{P3}}^{{\text{'}}} - X_{{B1}}^{{\text{'}}})}}^{2}} + {{{(Y_{{P3}}^{{\text{'}}} - Y_{{B1}}^{{\text{'}}})}}^{2}} + {{{(Z_{{P3}}^{{\text{'}}} - Z_{{B1}}^{{\text{'}}})}}^{2}}.} $

Исходя из изложенного, для определения положений точек выходного звена ${{P}_{i}}({{X}_{{Pi}}},~{{Y}_{{Pi}}},~{{Z}_{{Pi}}})$ (i = 1, 2, 3) в неподвижной системе координат $OXYZ$ рассмотрим три тетраэдра, имеющих общую плоскость основания, проходящую через точки ${{B}_{1}},{{B}_{2}},~{{B}_{3}}$ и вершины в точках ${{P}_{1}}$, ${{P}_{2}}$, ${{P}_{3}}$. Аналитическое решение задачи определения координат точек вершин указанных тетраэдров сводится к решению системы трех квадратных уравнений

$\left\{ {\begin{array}{*{20}{l}} {{{{({{X}_{{B1}}} - {{X}_{{P1}}})}}^{2}} + {{{({{Y}_{{B1}}} - {{Y}_{{P1}}})}}^{2}} + {{{({{Z}_{{B1}}} - {{Z}_{{P1}}})}}^{2}} = l_{{P1B1}}^{2},} \\ {{{{({{X}_{{B2}}} - {{X}_{{P1}}})}}^{2}} + {{{({{Y}_{{B2}}} - {{Y}_{{P1}}})}}^{2}} + {{{({{Z}_{{B2}}} - {{Z}_{{P1}}})}}^{2}} = l_{{P1B2}}^{2},} \\ {{{{({{X}_{{B3}}} - {{X}_{{P1}}})}}^{2}} + {{{({{Y}_{{B3}}} - {{Y}_{{P1}}})}}^{2}} + {{{({{Z}_{{B3}}} - {{Z}_{{P1}}})}}^{2}} = l_{{P1B3}}^{2},} \end{array}} \right.$
$\left\{ {\begin{array}{*{20}{l}} {{{{({{X}_{{B1}}} - {{X}_{{P2}}})}}^{2}} + {{{({{Y}_{{B1}}} - {{Y}_{{P2}}})}}^{2}} + {{{({{Z}_{{B1}}} - {{Z}_{{P2}}})}}^{2}} = l_{{P2B1}}^{2},} \\ {{{{({{X}_{{B2}}} - {{X}_{{P2}}})}}^{2}} + {{{({{Y}_{{B2}}} - {{Y}_{{P2}}})}}^{2}} + {{{({{Z}_{{B2}}} - {{Z}_{{P2}}})}}^{2}} = l_{{P2B2}}^{2},} \\ {{{{({{X}_{{B3}}} - {{X}_{{P2}}})}}^{2}} + {{{({{Y}_{{B3}}} - {{Y}_{{P2}}})}}^{2}} + {{{({{Z}_{{B3}}} - {{Z}_{{P2}}})}}^{2}} = l_{{P2B3}}^{2},} \end{array}} \right.$
$\left\{ {\begin{array}{*{20}{c}} {{{{({{X}_{{B1}}} - {{X}_{{P3}}})}}^{2}} + {{{({{Y}_{{B1}}} - {{Y}_{{P3}}})}}^{2}} + {{{({{Z}_{{B1}}} - {{Z}_{{P3}}})}}^{2}} = l_{{P3B1}}^{2},} \\ {{{{({{X}_{{B2}}} - {{X}_{{P3}}})}}^{2}} + {{{({{Y}_{{B2}}} - {{Y}_{{P3}}})}}^{2}} + {{{({{Z}_{{B2}}} - {{Z}_{{P3}}})}}^{2}} = l_{{P3B2}}^{2},} \\ {{{{({{X}_{{B3}}} - {{X}_{{P3}}})}}^{2}} + {{{({{Y}_{{B3}}} - {{Y}_{{P3}}})}}^{2}} + {{{({{Z}_{{B3}}} - {{Z}_{{P3}}})}}^{2}} = l_{{P3B3}}^{2}.} \end{array}} \right.$

Алгоритм решения системы квадратных уравнений аналогичен решению системы (1). Таким образом, можно считать, что положение выходного звена, заданное координатами точек P1, P2, P3, известно.

Следует отметить, что также важной является задача определения абсолютных координат, а именно, положения центра подвижной системы координат и углов ориентации координатных осей α, β, γ.

Для перехода от декартовых координат точек к абсолютным координатам сначала определим положение центра подвижной системы координат, что сопряжено с решением следующей системы уравнений

$\left\{ {\begin{array}{*{20}{l}} {{{{({{X}_{{P1}}} - {{X}_{{O'}}})}}^{2}} + {{{({{Y}_{{P1}}} - {{Y}_{{O'}}})}}^{2}} + {{{({{Z}_{{P1}}} - {{Z}_{{O'}}})}}^{2}} = l_{{P1O'~}}^{2},} \\ {{{{({{X}_{{P2}}} - {{X}_{{O'}}})}}^{2}} + {{{({{Y}_{{P2}}} - {{Y}_{{O'}}})}}^{2}} + {{{({{Z}_{{P2}}} - {{Z}_{{O'}}})}}^{2}} = l_{{P2O'}}^{2},} \\ {{{{({{X}_{{P3}}} - {{X}_{{O'}}})}}^{2}} + {{{({{Y}_{{P3}}} - {{Y}_{{O'}}})}}^{2}} + {{{({{Z}_{{P3}}} - {{Z}_{{O'}}})}}^{2}} = l_{{P3O'}}^{2},} \end{array}} \right.$
где ${{X}_{{O'}}}$, ${{Y}_{{O'}}}$, ${{Z}_{{O'}}}$ – искомые координаты начала $O{\text{'}}$ подвижной системы координат в неподвижной системе, а ${{l}_{{P1O'}}}$, ${{l}_{{P2O'}}}$, ${{l}_{{P3O'}}}$ – известные радиус-векторы точек P1, P2, P3 в подвижной системе координат. Система уравнений решается аналогично системе (1). Далее перенесем центр подвижной системы координат $O{\text{'}}$ и совместим с центром $~O$ неподвижной системы, что позволит определить углы ориентации.

Матрица 3 × 3, описывающая переход из подвижной системы к системе координат основания [6], имеет следующий вид

${\mathbf{M}} = \left( {\begin{array}{*{20}{c}} {\cos (\gamma )\cos (\beta )}&{\cos (\gamma )\sin (\beta )\sin (\alpha ) - \sin (\gamma )\cos (\alpha )}&{\sin (\gamma )\sin (\alpha ) + \cos (\gamma )\cos (\alpha )\sin (\beta )} \\ {\sin (\gamma )\cos (\beta )}&{\cos (\gamma )\cos (\alpha ) + \sin (\gamma )\sin (\beta )\sin (\alpha )}&{\sin (\gamma )\cos (\alpha )\sin (\beta ) - \cos (\gamma )\sin (\alpha )} \\ { - \sin (\beta )}&{\cos (\beta )\sin (\alpha )}&{\cos (\beta )\cos (\alpha )} \end{array}} \right).$

Это соответствует повороту подвижной системы вокруг оси $OX$ на угол α, затем на угол β вокруг повернутой оси $OY$ и на угол γ вокруг дважды повернутой оси $OZ$. Для определения этих углов запишем в матричном виде уравнения перехода между двумя системами координат для трех точек выходного звена, координаты которых известны и в подвижной, и неподвижной системах

${\mathbf{M}} \cdot \left( {\begin{array}{*{20}{c}} {X_{{Pi}}^{{\text{'}}}~} \\ {Y_{{Pi}}^{{\text{'}}}} \\ {Z_{{Pi}}^{{\text{'}}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{X}_{{Pi}}}} \\ {{{Y}_{{Pi}}}} \\ {{{Z}_{{Pi}}}} \end{array}} \right),\quad {\text{(здесь}}\;{\text{и}}\;{\text{далее}}\;i = 1,2,3{\text{)}}{\text{.}}$

В результате умножения матриц получим три тригонометрические уравнения с тремя неизвестными углами, всего будет девять уравнений, которые имеют вид

$\begin{gathered} X_{{Pi}}^{{\text{'}}}\cos ({\gamma })\cos ({\beta }) + Y_{{Pi}}^{{\text{'}}}(\cos ({\gamma })\sin {\text{(}}\beta {\text{)}}\sin ({\alpha }) - \sin {\text{(}}\gamma {\text{)}}\cos ({\alpha })) + ~ \\ + \;Z_{{Pi}}^{{\text{'}}}(\sin {\text{(}}\gamma {\text{)}}\sin ({\alpha }) + \cos ({\gamma })\cos ({\alpha })\sin {\text{(}}\beta {\text{)}}) = ~{{X}_{{Pi}}}, \\ \end{gathered} $
$\begin{gathered} X_{{Pi}}^{{\text{'}}}\sin {\text{(}}\gamma {\text{)}}\cos ({\beta }) + Y_{{Pi}}^{{\text{'}}}(\cos ({\gamma })\cos {\text{(}}\alpha {\text{)}} + \sin ({\gamma })\sin {\text{(}}\beta {\text{)}}\sin ({\alpha })) + ~ \\ + \;Z_{{Pi}}^{{\text{'}}}(\sin {\text{(}}\gamma {\text{)}}\cos ({\alpha })\sin {\text{(}}\beta {\text{)}} - \cos {\text{(}}\gamma {\text{)}}\sin ({\alpha })) = {{Y}_{{Pi}}}, \\ \end{gathered} $
$ - X_{{Pi}}^{{\text{'}}}\sin (\beta ) + Y_{{Pi}}^{{\text{'}}}\cos (\beta )\sin (\alpha ) + Z_{{Pi}}^{{\text{'}}}\cos (\beta )\cos (\alpha ) = {{Z}_{{Pi}}}.$

Далее рассмотрим три уравнения, связывающие координаты ${{Z}_{{Pi}}}$ и углы α, β, γ

$ - X_{{P1}}^{'}\sin (\beta ) + Y_{{P1}}^{{\text{'}}}\cos (\beta )\sin (\alpha ) + Z_{{P1}}^{{\text{'}}}\cos (\beta )\cos (\alpha ) = {{Z}_{{P1}}},$
$ - X_{{P2}}^{{\text{'}}}\sin (\beta ) + Y_{{P2}}^{{\text{'}}}\cos (\beta )\sin (\alpha ) + Z_{{P2}}^{{\text{'}}}\cos (\beta )\cos (\alpha ) = {{Z}_{{P2}}},$
$ - X_{{P3}}^{{\text{'}}}\sin (\beta ) + Y_{{P3}}^{{\text{'}}}\cos (\beta )\sin (\alpha ) + Z_{{P3}}^{{\text{'}}}\cos (\beta )\cos (\alpha ) = {{Z}_{{P3}}}.$

Введем следующие обозначения

$\sin {\text{(}}\beta {\text{)}} = {{m}_{1}},$
$\cos ({\beta })\sin {\text{(}}\alpha {\text{)}} = {{m}_{2}},$
$\cos ({\beta })\cos {\text{(}}\alpha {\text{)}} = {{m}_{3}}.$

Тогда получим

$\left( {\begin{array}{*{20}{c}} { - X_{{P1}}^{{\text{'}}}}&{Y_{{P1}}^{{\text{'}}}}&{Z_{{P1}}^{{\text{'}}}} \\ { - X_{{P2}}^{{\text{'}}}}&{Y_{{P2}}^{{\text{'}}}}&{Z_{{P2}}^{{\text{'}}}} \\ { - X_{{P3}}^{{\text{'}}}}&{Y_{{P3}}^{{\text{'}}}}&{Z_{{P3}}^{{\text{'}}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {m1} \\ {m2} \\ {m3} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{Z}_{{P1}}}} \\ {{{Z}_{{P2}}}} \\ {{{Z}_{{P3}}}} \end{array}} \right),$
откуда находим

$\left( {\begin{array}{*{20}{c}} {m1} \\ {m2} \\ {m3} \end{array}} \right) = {{\left( {\begin{array}{*{20}{c}} { - X_{{P1}}^{{\text{'}}}}&{Y_{{P1}}^{{\text{'}}}}&{Z_{{P1}}^{{\text{'}}}} \\ { - X_{{P2}}^{{\text{'}}}}&{Y_{{P2}}^{{\text{'}}}}&{Z_{{P2}}^{{\text{'}}}} \\ { - X_{{P3}}^{{\text{'}}}}&{Y_{{P3}}^{{\text{'}}}}&{Z_{{P3}}^{{\text{'}}}} \end{array}} \right)}^{{ - 1}}}\left( {\begin{array}{*{20}{c}} {{{Z}_{{P1}}}} \\ {{{Z}_{{P2}}}} \\ {{{Z}_{{P3}}}} \end{array}} \right).$

Рассматривая обратную матрицу, можно написать, что

$\beta = ~\arcsin ({{m}_{1}}),$
${\alpha } = ~\arcsin ({{m}_{2}}{\text{/}}\cos ({\beta })).$

Для нахождения угла ${\gamma }$ рассмотрим систему из трех уравнений

$\begin{gathered} X_{{P1}}^{{\text{'}}}\sin {\text{(}}\gamma {\text{)}}\cos ({\beta }) + Y_{{P1}}^{{\text{'}}}(\cos ({\gamma })\cos {\text{(}}\alpha {\text{)}} + \sin ({\gamma })\sin {\text{(}}\beta {\text{)}}\sin ({\alpha })) + ~ \\ + \;Z_{{P1}}^{{\text{'}}}(\sin {\text{(}}\gamma {\text{)}}\cos ({\alpha })\sin {\text{(}}\beta {\text{)}} - \cos {\text{(}}\gamma {\text{)}}\sin ({\alpha })) = {{Y}_{{P1}}}, \\ \end{gathered} $
$\begin{gathered} X_{{P2}}^{{\text{'}}}\sin {\text{(}}\gamma {\text{)}}\cos ({\beta }) + Y_{{P2}}^{{\text{'}}}(\cos ({\gamma })\cos {\text{(}}\alpha {\text{)}} + \sin ({\gamma })\sin {\text{(}}\beta {\text{)}}\sin ({\alpha })) + ~ \\ + \;Z_{{P2}}^{{\text{'}}}(\sin {\text{(}}\gamma {\text{)}}\cos ({\alpha })\sin {\text{(}}\beta {\text{)}} - \cos {\text{(}}\gamma {\text{)}}\sin ({\alpha })) = {{Y}_{{P2}}}, \\ \end{gathered} $
$\begin{gathered} X_{{P3}}^{{\text{'}}}\sin {\text{(}}\gamma {\text{)}}\cos ({\beta }) + Y_{{P3}}^{{\text{'}}}(\cos ({\gamma })\cos {\text{(}}\alpha {\text{)}} + \sin ({\gamma })\sin {\text{(}}\beta {\text{)}}\sin ({\alpha })) + ~ \\ + \;Z_{{P3}}^{{\text{'}}}(\sin {\text{(}}\gamma {\text{)}}\cos ({\alpha })\sin {\text{(}}\beta {\text{)}} - \cos {\text{(}}\gamma {\text{)}}\sin ({\alpha })) = {{Y}_{{P3}}}. \\ \end{gathered} $

Обозначим

$\sin {\text{(}}\gamma {\text{)}}\cos ({\beta }) = {{s}_{1}},$
$\cos ({\gamma })\cos {\text{(}}\alpha {\text{)}} + \sin ({\gamma })\sin {\text{(}}\beta {\text{)}}\sin ({\alpha }) = {{s}_{2}},$
$(\sin {\text{(}}\gamma {\text{)}}\cos ({\alpha })\sin {\text{(}}\beta {\text{)}} - \cos {\text{(}}\gamma {\text{)}}\sin ({\alpha }) = {{s}_{3}}.$

Тогда получим

$\left( {\begin{array}{*{20}{c}} {s1} \\ {s2} \\ {s3} \end{array}} \right) = {{\left( {\begin{array}{*{20}{c}} {X_{{P1}}^{{\text{'}}}}&{Y_{{P1}}^{{\text{'}}}}&{Z_{{P1}}^{{\text{'}}}} \\ {X_{{P2}}^{{\text{'}}}}&{Y_{{P2}}^{{\text{'}}}}&{Z_{{P2}}^{{\text{'}}}} \\ {X_{{P3}}^{{\text{'}}}}&{Y_{{P3}}^{{\text{'}}}}&{Z_{{P3}}^{{\text{'}}}} \end{array}} \right)}^{{ - 1}}}\left( {\begin{array}{*{20}{c}} {{{Y}_{{P1}}}} \\ {{{Y}_{{P2}}}} \\ {{{Y}_{{P3}}}} \end{array}} \right).$

Отсюда находим неизвестный угол ${\gamma }$

${\gamma } = \arcsin \left( {{{s}_{1}}{\text{/}}\cos ({\beta })} \right).$

Следует учесть, что обратная функция arcsin на интервале [–π/2; +π/2] определена однозначно.

Таким образом прямая задача о положениях решена, а также определены абсолютные координаты выходного звена механизма.

Рассмотрим пример. Известны координаты точек P1, P2, P3 выходного звена в подвижной системе координат: $P_{1}^{{\text{'}}}\left( {1~~0~~0} \right)$; $P_{2}^{{\text{'}}}\left( {0~~1~~0} \right)$; $P_{3}^{{\text{'}}}\left( {0~~0~~1} \right)$. По указанному алгоритму определены координаты этих точек в неподвижной системе координат

${{P}_{1}}\left( {0.3536\,\;0.6124\,\; - {\kern 1pt} 0.7071} \right),$
${{P}_{2}}\left( { - 0.5732\;\,0.7392\;\,0.3536} \right),$
${{P}_{3}}\left( {0.7392\;\,0.2803\;\,0.6124} \right).$

Расчет углов ориентации подвижной системы координат в отношении неподвижной системы дает следующий результат

${\alpha } = {\text{\;}}30.004^\circ \quad {\beta } = 44.99^\circ \quad {\gamma } = 60.003^\circ .$

Таким образом, в данной статье приведено аналитическое решение прямой задачи о положениях для l-координатного механизма обычного вида, а также для механизма, где выходное звено и приводы расположены по разные стороны от основания. Аналитическое решение прямой задачи о положениях упрощает методику составления уравнений движения механизма, что дает преимущество при решении задач динамического управления движением [13].

Список литературы

  1. Hunt K. Structural kinematics of in-parallel-actuated robot arms // ASME. Journal of Mechanisms, Transmissions, and Automation in Design. 1983. V. 105. P. 705.

  2. Merlet J.P. Singular configurations of parallel manipulators and Grassman geometry // Intern. J. Robotic Res. 1989. V. 8. Iss. 5. P. 45.

  3. Алешин А.К., Глазунов В.А., Рашоян Г.В., Оффер Ш. Анализ кинематических винтов, определяющих топологию сингулярных зон роботов параллельной структуры // Ж. Проблемы машиностроения и надежности машин. 2016. № 4. С. 3.

  4. Алешин А.К., Глазунов В.А., Рашоян Г.В., Оффер Ш., Скворцов С.А. Анализ элементарных перемещений манипулятора параллельной структуры с круговой направляющей на основе дифференцирования уравнения связей // Ж. Проблемы машиностроения и надежности машин. 2016. № 5. С. 17.

  5. Rashoyan G.V., Shalyukhin K.A., Gaponenko E.V. Development of structural schemes of parallel structure manipulators using screw calculus. IOP Conference Series: Materials Science and Engineering. 2018. V. 327. Iss. 4.

  6. Новые механизмы в современной робототехнике / Под редакцией В.А. Глазунова. М.: Техносфера. 2018. С. 314.

  7. Антонов А.В., Глазунов В.А., Алешин А.К., Рашоян Г.В., Лактионова М.М. Кинематический анализ механизма параллельной структуры для работы в агрессивных средах // Ж. Проблемы машиностроения и надежности машин. 2018. № 2. С. 3.

  8. Рашоян Г.В., Алешин А.К., Скворцов С.А., Левин С.В., Антонов А.В., Шалюхин К.А. Задачи кинематического анализа и особых положений механизмов роботов параллельной структуры // Ж. Проблемы машиностроения и надежности машин. 2018. № 4. С. 11.

  9. Ganiev R.F., Glazunov V.A., Filippov G.S. Urgent Problems of Machine Science and Ways of Solving Them: Wave and Additive Technologies, the Machine Tool Industry, and Robot Surgery // J. of Machinery Manufacture and Reliability. 2018. V. 47. Iss. 5. P. 399.

  10. Glazunov V., Nosova N., Kheylo S., Tsarkov A. Design and Analysis of the 6-DOF Decoupled Parallel Kinematics Mechanism // J. Mechanisms and Machine Science. 2018. V. 56. P. 125.

  11. Glazunov V.A., Borisov V.A. Development of Parallel-Structure Mechanisms with Four Degrees of Freedom and Four Kinematic Chains // Journal of Machinery Manufacture and Reliability. 2017. V. 46. Iss. 5. P. 417.

  12. Арзуманян К.С., Колискор А.Ш. Синтез структур l-координатных систем для исследования и диагностирования промышленных роботов // Ж. Испытания, контроль и диагностирование гибких производственных систем. М.: Наука, 1988. С. 70.

  13. Siciliano B., Khatib O. Springer Handbook of Robotics. Springer International Publishing. 2016. P. 2227.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал