Проблемы машиностроения и надежности машин, 2019, № 6, стр. 59-70
ОБ ОПИСАНИИ ВИБРАЦИОННЫХ ПОЛЕЙ В РЕШЕТЧАТЫХ 2D-КОНСТРУКЦИЯХ С ТРЕУГОЛЬНЫМИ (ГЕКСАГОНАЛЬНЫМИ) ЯЧЕЙКАМИ
В. Л. Крупенин *
Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия
* E-mail: krupeninster@gmail.com
Поступила в редакцию 30.05.2019
Принята к публикации 08.08.2019
Аннотация
Статья посвящена проблеме описания вибрационных полей в струнных решетках с треугольными (центрированными гексагональными) ячейками. Задачи такого рода достаточно мало изучены, несмотря на то, что необходимые модели находят применение при динамическом анализе разнообразных машин и конструкций, а также в кристаллографии и материаловедении. Приведены уравнения движения. Рассмотрены задачи о распространении синусоидальных волн и вынужденных колебаниях в условиях силового широкополосного случайного воздействия.
1. Решетчатые конструкции широко распространены в авиа- и судостроении, во многих других отраслях современного машиностроения, в строительстве и сельском хозяйстве. Важный подкласс таких систем – плоские 2D-решетки. Они определяют конструкции ряда горных, просеивающих и сортировочных машин, с их помощью проводится моделирование многочисленных 2D-объектов – мембран, пластин, панелей, строительных конструкций. Кроме того, при их посредстве могут анализироваться волны в метаматериалах, композитных материалах с периодическим армированием, кристаллах, а также наноструктурированных поверхностных и приповерхностных слоях конструкционных материалов [1–7]. Этот перечень можно существенно продолжить. Вместе с тем, динамический анализ решетчатых конструкций по ряду причин не получил необходимого распространения, а работы, касающиеся динамики решетчатых конструкций с учетом соударений их узлов достаточно редки [8–10].
Динамическое поведение плоских решеток существенно зависит от их структурных особенностей, в частности от типов ячеек решеток. В настоящей статье рассмотрены, в основном, задачи динамики струнных решеток с треугольными ячейками (центрированными гексагональными). Приведены уравнения движения для дискретных и континуальных моделей, дан подробный анализ задачи о вынужденных случайных колебаниях решетки, вибрирующей вблизи ограничителя хода под действием широкополосных случайных сил в предположении применимости методов диффузионных марковских процессов.
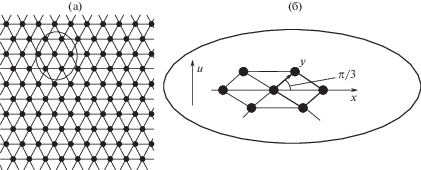
2. Рассмотрим струнную решетку, составленную из трех семейств упругих линейных струн, образующих правильные треугольные ячейки (рис. 1a). Выберем на решетке декартову остроугольную систему координат, образованную осями x и y, расположенными друг к другу под углом π/3 (рис. 1б). Для идентификации узлов решетки, очевидно, достаточно двух текущих индексов. Обозначим их k = 0, 1, 2, …, N1 и q = 0, 1, 2, …, N2, предположив что индекс k нумерует вдоль оси x, а индекс q – оси y.
Пусть узлы – суть абсолютно твердые тела с массами ${{m}_{{kq}}} \equiv m$. Будем искать их перемещения (прогибы) вдоль осей, расположенных перпендикулярно плоскости решетки.
Струнные элементы ячеек предполагаются безынерционными. Крепления струн в узлах считаются абсолютно жесткими, а натяжения – настолько большими, что их изменениями при осуществлении линейных колебаний можно пренебречь.
Обозначим натяжения каждого пролета струны τ, а длины сторон треугольников – a. Тогда коэффициент упругости с = τa–1.
Каждый узел, находящийся внутри решетки имеет шесть равнозначных соседних узлов, поэтому систему можно трактовать как гексагональную центрированную решетку [11, 12]. Функция Лагранжа решетки имеет вид
(1)
$L{\text{(}}{{u}_{{kq}}}{\text{,}}{{\dot {u}}_{{kq}}}{\text{)}} = {{T}_{{\text{*}}}}{\text{(}}{{\dot {u}}_{{kq}}}{\text{)}} - {{U}_{{\text{*}}}}{\text{(}}{{u}_{{kq}}}{\text{)}} = \frac{{\text{1}}}{{\text{2}}}m\sum\limits_{k = 1}^{{{N}_{1}}} {\sum\limits_{q = 1}^{{{N}_{2}}} {\dot {u}_{{_{{kq}}}}^{2}} } - \frac{{\text{1}}}{{\text{2}}}c\sum\limits_{k = 1}^{{{N}_{1}}} {\sum\limits_{q = 1}^{{{N}_{2}}} {\sum\limits_{n = 1}^6 {D{}_{n}^{2}(u_{{kq}}^{{}})} } } ,$Пусть в узлах приложены внешние силы, представимые через операторные функции gkq($d{\text{/}}dt$; t, $u_{{kq}}^{{}}$). Тогда для изгибных колебаний решетки получаем уравнения движения
(2)
$\begin{gathered} m{{{\ddot {u}}}_{{kq}}} + c(6{{u}_{{kq}}} - {{u}_{{(k - 1,q)}}} - {{u}_{{(k + 1,q)}}} - {{u}_{{(k,q - 1)}}} - {{u}_{{(k,q + 1)}}} - {{u}_{{(k - 1,q - 1)}}} - {{u}_{{(k + 1,q + 1)}}}) = \\ = {{g}_{{kq}}}(d{\text{/}}dt;t,{{u}_{{kq}}}).{\text{ }} \\ \end{gathered} $При рассмотрении краевой задачи, например, в случае решетки, имеющей форму параллелограмма, считая струны на концах защемленными (на рис. 1 не показано), примем
Контур защемления может иметь и другую структуру. При этом форма записи (3) сохранится, но в случае усложнения структуры контура к ней могут добавиться очевидные дополнительные соотношения. При необходимости сюда можно присоединить начальные условия.
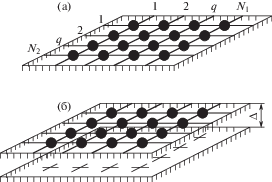
Рассматриваемая система аналогична решетчатой конструкции с квадратными (прямоугольными) ячейками (рис. 2а) [8–10]. Уравнения движения для прогибов решетки с квадратными ячейками имеют вид
(4)
$m{{\ddot {u}}_{{kq}}} + c{\text{(}}4{{u}_{{kq}}} - {{u}_{{(k - 1,q)}}} - {{u}_{{(k + 1,q)}}} - {{u}_{{(k,q - 1)}}} - {{u}_{{(k,q + 1)}}}{\text{)}} = {{g}_{{kq}}}{\text{(}}d{\text{/}}dt;t,{{u}_{{kq}}}{\text{);}}\quad с = a{{\tau }^{{ - 1}}},$3. Перейдем к континуальному аналогу задачи (2), (3). Предположим, что число струн, образующих решетку велико, т.е. ее локальная структурная характеристика (длина стороны треугольной ячейки a) малая величина. Одновременно усредненные характеристики решетки (поверхностная плотность (масса единицы площади) $\rho = m{\text{/}}{{a}^{2}}$ и упругость пролетов с) не малы. Постулируем предположение, что существует требуемое число раз непрерывно-дифференцируемая функция $u(x,y,t)$, совпадающая в узлах решетки с дискретной физической переменной ${{u}_{{kq}}} = u{\text{(}}x,y,t{\text{)}}$. При этом, с точностью до бесконечно малых ($O{\text{(}}{{a}^{2}}{\text{)}}$)
(5)
${{u}_{{{\text{(}}k \pm 1,q{\text{)}}}}} = u{\text{(}}x \pm a,y,t{\text{);}}\quad {{u}_{{{\text{(}}k,q \pm 1{\text{)}}}}} = u{\text{(}}x,y \pm a,t{\text{)}};\quad {{u}_{{{\text{(}}k \pm 1,q \pm 1{\text{)}}}}} = u{\text{(}}x \pm a,y \pm a,t{\text{)}}{\text{.}}$(6)
$\begin{gathered} \rho {{u}_{{tt}}} - c[u_{{xx}}^{{}}(x,y,t) + u_{{xy}}^{{}}(x,y,t) + {\text{ }}u_{{yy}}^{{}}(x,y,t)] - \\ - \;\frac{{c{{a}^{2}}}}{{12}}[u_{{4x}}^{{}}(x,y,t) + u_{{2x2y}}^{{}}(x,y,t) + {\text{ }}u_{{4y}}^{{}}(x,y,t)] + O({{a}^{6}}) = g{}_{0}[x,y;\partial {\text{/}}\partial t;t,u(x,y,t)], \\ \end{gathered} $Граничные условия (3) переходят в условия
где P контур, на котором находятся, защемленные граничные узлы решетки – параллелограмм или какой-то иной контур защемления.Член, содержащий высшие производные в уравнении (6) позволяет учесть специфику исходной решетчатой конструкции (он пропорционален параметру решетки a) и важен при рассмотрении высокочастотных колебаний. Часто подобными членами целесообразно пренебречь и упростить задачу, записав вместо уравнения (6), уравнение
(8)
$\rho {{u}_{{tt}}} - c[u_{{xx}}^{{}}(x,y,t) + u_{{xy}}^{{}}(x,y,t) + u_{{yy}}^{{}}(x,y,t)] = {{g}_{0}}[x,y;\partial {\text{/}}\partial t;t,u(x,y,t)].$(9)
$u(x,y,t) = B\exp {\text{[}}i{\text{(}}{{K}_{{\text{1}}}}x + {{K}_{2}}y - \omega t{\text{)];}}\quad {\text{B}} = {\text{const}} > {\text{0}},$Для системы (6)
(11)
$\rho {{\omega }^{2}} = с(K_{1}^{2}K_{2}^{2} + {{K}_{1}}{{K}_{2}}) + \frac{{c{{a}^{2}}}}{{12}}(K_{1}^{4} + K_{2}^{4} + K_{{_{1}}}^{4}K_{{_{2}}}^{4}).$Отметим, что длинноволновые приближения для уравнений движения решетки с квадратными ячейками (4) дадут вместо (8) и (6) соответственно уравнения мембраны
(12)
$\rho {{u}_{{tt}}} - c[u_{{xx}}^{{}}(x,y,t) + u_{{yy}}^{{}}(x,y,t)] = {{g}_{0}}[x,y;\partial {\text{/}}\partial t;t,u(x,y,t)];$(13)
$\begin{gathered} \rho {{u}_{{tt}}} - c[u_{{xx}}^{{}}(x,y,t) + u_{{yy}}^{{}}(x,y,t)] - \frac{{c{{a}^{2}}}}{{12}}[u_{{4x}}^{{}}(x,y,t) + u_{{4y}}^{{}}(x,y,t)] + O({{a}^{6}}) = \\ = g{}_{0}[x,y;\partial {\text{/}}\partial t;t,u(x,y,t)]. \\ \end{gathered} $При этом дисперсионные соотношения принимают вид
(14)
$\rho {{\omega }^{2}} = с(K_{1}^{2} + K_{2}^{2}){\text{,}}\quad \rho {{\omega }^{2}} = с(K_{1}^{2} + K_{2}^{2}) + \frac{{c{{a}^{2}}}}{{12}}(K_{1}^{4} + K_{2}^{4}).$Для основной дискретной модели треугольной решетки, полагая
(15)
${{u}_{{kn}}}(t) = B\exp {\text{[}}i{\text{(}}{{K}_{{\text{1}}}}k + {{K}_{2}}n - \omega t{\text{)];}}\quad {\text{B}} = {\text{const}} > {\text{0}},$(16)
$m{{\omega }^{2}} = 4{{\sin }^{2}}\frac{1}{2}K_{2}^{{}} + 4{{\sin }^{2}}\frac{1}{2}K_{1}^{{}} - 4{{\sin }^{2}}\frac{1}{2}{{{\text{(}}K_{1}^{{}} + K_{2}^{{}}{\text{)}}}^{{\text{2}}}}.$Рассмотрим вопрос о том, как соотносятся между собой модели решеток с треугольными и квадратными ячейками. Возьмем модели, отвечающие уравнениям (8) и (12). Их можно объединить посредством введения некоторого безразмерного множителя перед смешанной производной (обозначим его $\sigma $). В квадратной скобке, входящей в левую часть уравнения (8) появляется член $\sigma u_{{xy}}^{{}}(x,y,t)$. Пусть $\sigma \in {\text{[0,1]}}$. Если $\sigma $ = 1, то имеем модель (8), при $\sigma \to 0$ приходим к модели (12).
Если ввести тот же параметр $\sigma $ перед разностями ${\text{(}}{{u}_{{kq}}} - {{u}_{{(k + 1,q + 1)}}}{\text{)}}$ и (${{u}_{{kq}}} - {{u}_{{(k - 1,q - 1)}}})$, то модель решетки с треугольными ячейками (уравнение (2)) перейдет в модель с квадратными ячейками (уравнение (4)).
Корректное описание преобразования решетки при изменении параметра $\sigma $ – нетривиально, так как несмотря на то, что треугольная и прямоугольная ячейки – топологически эквивалентны [13] (рис. 3) и могут быть непрерывно деформированы одна в другую, придать однозначный физический смысл промежуточным значениям параметра $\sigma \in {\text{(0,1)}}$ без постулирования дополнительных гипотез проблематично. Относящиеся сюда вопросы – не рассматриваются.
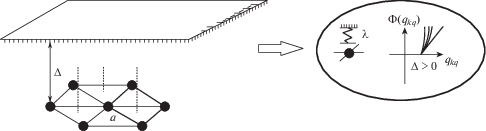
4. Дальнейшие рассмотрения касаются только модели (2) и случая вынужденных случайных колебаний, происходящих в вязкой среде. Будем предполагать, что вблизи каждого из узлов решетки с зазором $\Delta \geqslant 0$ установлен, вообще говоря, податливый ограничитель хода (рис. 4; показана одна гексагональная ячейка решетки). Пусть возбуждение колебаний осуществляется за счет действия на все узлы случайных сил, описываемых стационарными стандартными белыми шумами с нулевым средним. Взаимодействие узлов решетки с ограничителями предполагается упругим. Виброударный вариант модели (4) (рис. 2б) рассматривался ранее в работах [8–10].
Будем использовать канонические переменные ${{u}_{{kq}}} \equiv {{q}_{{kq}}}$; ${{p}_{{kq}}} = m{{\dot {u}}_{{kq}}}$. Пусть $\lambda {\text{П(}}q_{{kq}}^{{}}{\text{)}}$ потенциальная энергия силы упругого ударного взаимодействия, определяемого гипотезой удара, $\lambda \gg 1$ – большой параметр. Считая, что принятые гипотезы взаимодействия (удара) во всех ударных парах одинаковы, сможем записать
(17)
$\lambda {\text{П(}}q_{{kq}}^{{}}{\text{)}} = \lambda \int\limits_0^{{{q}_{{kq}}}} {\text{Ф}} {\text{(}}z{\text{)}}dz,$Установление гипотезы удара – это мотивированное задание представления силы взаимодействия. Если, например, ударная пара – односторонняя и несимметричная, то несимметричной будет и, отвечающая ей, пороговая функция $\lambda {{{\text{Ф}}}_{{kq}}}({{q}_{k}})$ (рис. 4), при посредстве которой, собственно, и устанавливается гипотеза удара в данной ударной паре. Класс пороговых функций {Ф}Δ для данной задачи определяется так
При $\lambda \to \infty $ гипотеза взаимодействия переходит в гипотезу Ньютона для абсолютно упругого удара. Т.е. конфигурационное пространство системы $\Re $ задается при помощи неравенств
(18)
$\Re = \{ {{q}_{{kq}}} \leqslant \Delta \} ;\quad k = 0,\;...,\;{{N}_{1}};\quad q = 0,\;...,\;{{N}_{2}}.$Полагая, что решетка помещена в некоторую вязкую среду, создающую сопротивление, пропорциональное абсолютной скорости узла с коэффициентом пропорциональности равным 2b, запишем, учитывая также переход к каноническим переменным, представление для сил, входящих в уравнения движения (2)
Для консервативной части системы функцию Гамильтона $H({{q}_{{kq}}},{{p}_{{kq}}})$ легко определить, исходя из вида функции Лагранжа (1) и формулы (17), а также предположения, что потери энергии при соударениях в каждой ударной паре не учитываются
(19)
$H({{q}_{{kq}}},{{p}_{{kq}}}) = {{T}_{{\text{*}}}}({{p}_{{kq}}}) + {{U}_{0}}_{{\text{*}}}({{q}_{{kq}}}) = \frac{1}{2}\sum\limits_{k = 1}^{{{N}_{1}}} {\sum\limits_{q = 1}^{{{N}_{2}}} {p_{{kq}}^{2} + } } \frac{1}{2}c\sum\limits_{k = 1}^{{{N}_{1}}} {\sum\limits_{q = 1}^{{{N}_{2}}} {\sum\limits_{n = 1}^6 {D{}_{n}^{2}(q_{{kq}}^{{}})} } } + \lambda \sum\limits_{k = 1}^{{{N}_{1}}} {\sum\limits_{q = 1}^{{{N}_{2}}} {\Pi (q_{{kq}}^{{}})} } .$(20)
$\frac{{d{{q}_{{kq}}}}}{{dt}} = \frac{{\partial H}}{{\partial {{p}_{{kq}}}}};\quad \frac{{d{{p}_{{kq}}}}}{{dt}} = - \frac{{\partial H}}{{\partial {{q}_{{kq}}}}} - 2b{{p}_{{kq}}} + {{\xi }_{{kq}}}.$Воспользуемся методами диффузионных марковских процессов и запишем уравнение ФПК для w(t, qkq, pkq) – совместной плотности вероятностей многомерного случайного процесса {qkq(t), pkq(t)} [16–19], которая и определяет состояние решетки
(21)
$\frac{{\partial P}}{{\partial t}} + \sum\limits_{k = 1}^{{{N}_{1}}} {\sum\limits_{q = 1}^{{{N}_{2}}} {\left[ {{{{\left\{ {H,w} \right\}}}_{{kq}}} - 2b\frac{{\partial ({{p}_{{kq}}}w)}}{{\partial {{p}_{{kqi}}}}} - 2S\frac{{{{\partial }^{2}}w}}{{\partial p_{{kq}}^{2}}}} \right]} } = 0;\quad {{\{ A,B\} }_{{kq}}} = \frac{{\partial A}}{{\partial {{p}_{{kq}}}}}\frac{{\partial B}}{{\partial {{q}_{{kq}}}}} - \frac{{\partial A}}{{\partial {{q}_{{kq}}}}}\frac{{\partial B}}{{\partial {{p}_{{kq}}}}}$Как известно [16], для стационарного процесса, когда $\frac{{\partial P}}{{\partial t}} = 0$, уравнение (6) имеет точное решение, которое дается каноническим распределением Гиббса
(22)
$P({{{\mathbf{q}}}_{{kq}}},{{{\mathbf{p}}}_{{kq}}}) = Сехp\left[ { - \frac{{2b}}{S}Н({{{\mathbf{q}}}_{{kq}}},{{{\mathbf{p}}}_{{kq}}})} \right],$Хорошо известно (и это видно из формул (19) и (22)), что импульсы и координаты – статистически независимы.
Распределение Гиббса после интегрирования по всем координатам дает нормальное распределение по импульсным переменным (распределение Максвелла): кинетическая энергия, стоящая в показателе экспоненты, зависит только от квадратов импульсов
(23)
$P({{{\mathbf{p}}}_{{kq}}}) = {{C}_{1}}\exp \left\{ { - \frac{{2b}}{S}\sum\limits_{k = 1}^{{{N}_{1}}} {\sum\limits_{q = 1}^{{{N}_{2}}} {p_{{kq}}^{2}} } } \right\};\quad {{C}_{1}} = {{\left[ {\frac{{2b}}{{{\pi }S}}} \right]}^{{{\text{0}}{\text{.5}}N}}},\quad N = {{N}_{1}}{{N}_{2}}.$5. Обратимся, после интегрирования распределения (22) по всем обобщенным импульсам, к распределению Больцмана по обобщенным координатам
(24)
$w{\text{(}}{\mathbf{q}}_{{kq}}^{{}}{\text{)}} = {{C}_{{\text{2}}}}\exp \left\{ { - 2b{{S}^{{ - {\text{1}}}}}\left[ {\frac{{\text{1}}}{{\text{2}}}c\sum\limits_{k = 1}^{{{N}_{1}}} {\sum\limits_{q = 1}^{{{N}_{2}}} {\sum\limits_{n = 1}^6 {D{}_{n}^{2}{\text{(}}q_{{kq}}^{{}}{\text{)}}} } } + {\lambda }\sum\limits_{k = 1}^{{{N}_{1}}} {\sum\limits_{q = 1}^{{{N}_{2}}} {\Pi {\text{(}}q_{{kq}}^{{}}{\text{)}}} } } \right]} \right\},$Для нахождения плотностей вероятностей низших измерений необходимо выполнить необходимое число интегрирований функции плотности (24) по неинтересующим координатам.
Обычно характеристика нагружения в зоне взаимодействия представляется в виде степенной функции [14, 15]. Тогда потенциальная энергия упругого взаимодействия дается кусочно-степенной функцией
(25)
$w{\text{(}}{{{\mathbf{q}}}_{{kq}}}{\text{)}} = {{C}_{{\text{2}}}}\exp \left\{ { - b{{S}^{{ - {\text{1}}}}}\left[ {c\sum\limits_{k = 1}^{{{N}_{1}}} {\sum\limits_{q = 1}^{{{N}_{2}}} {\sum\limits_{n = 1}^6 {D{}_{n}^{2}{\text{(}}q_{{kq}}^{{}}{\text{)}} + \lambda \sum\limits_{k = 1}^{{{N}_{1}}} {\sum\limits_{q = 1}^{{{N}_{2}}} {{{{{\text{(}}q_{{kq}}^{{}} - \Delta {\text{)}}}}^{\alpha }}\eta {\text{(}}q_{{kq}}^{{}} - \Delta {\text{)}}} } } } } } \right]} \right\},\quad {\alpha } \geqslant {\text{1}}{\text{.}}$Функция распределения координат
(26)
$W{\text{(}}{{{\mathbf{q}}}_{{kq}}}{\text{)}} = \int\limits_{ - \infty }^{{{{\mathbf{q}}}_{{kq}}}} {w{\text{(}}{{{\mathbf{z}}}_{{kq}}}{\text{)}}} d{{{\mathbf{z}}}_{{kq}}} = {\mathbf{P}}{\text{\{ }}{{{\mathbf{q}}}_{{\text{*}}}}_{{kq}} < {{{\mathbf{q}}}_{{kq}}}{\text{\} ,}}$Отсюда видно, что вероятность существования конфигурации с превышением порога $\Delta $ для всех узлов решетки есть
(27)
${\mathbf{P}}{\text{\{ }}{{{\mathbf{q}}}_{{kq}}} > {\mathbf{\Delta }}{\text{\} }} = {\text{1}} - W(\Delta ),$Внося (25) в (26), и далее, внося результат в (29) находим
(28)
$\begin{gathered} {\mathbf{P}}{\text{\{ }}{{{\mathbf{q}}}_{{kq}}} > {\mathbf{\Delta }}{\text{\} }} = \\ = 1 - {{C}_{2}}\int\limits_{ - \infty }^{\mathbf{\Delta }} {{\text{exp}}\left\{ { - bc{{S}^{{ - {\text{1}}}}}\left[ {c\sum\limits_{k = 1}^{{{N}_{1}}} {\sum\limits_{q = 1}^{{{N}_{2}}} {\sum\limits_{n = 1}^6 {D{}_{n}^{2}{\text{(}}z_{{kq}}^{{}}{\text{)}}} } } + {\lambda }\sum\limits_{k = 1}^{{{N}_{1}}} {\sum\limits_{q = 1}^{{{N}_{2}}} {{{{{\text{(}}z_{{kq}}^{{}} - \Delta {\text{)}}}}^{{\alpha }}}{\eta (}z_{{kq}}^{{}} - \Delta {\text{)}}} } } \right]} \right\}} d{{{\mathbf{z}}}_{{kq}}} \\ \end{gathered} $При больших λ оценка вероятности (28) есть [21]
(29)
${\mathbf{P}}{\text{\{ }}{{{\mathbf{q}}}_{{kq}}} > {\mathbf{\Delta }}{\text{\} }} = O{\text{(}}{{{\lambda }}^{{ - N}}}{\text{);}}\quad N = {{N}_{1}}{{N}_{2}};\quad \lambda \to \infty .$Если ${\lambda } \to \infty $, то высокие при конечных $\lambda $ потенциальные барьеры, $\lambda {\text{П(}}q_{{kq}}^{{}}{\text{)}}$ приобретают высоты равные кинетическим энергиям каждого из узлов и становятся непроницаемыми [9, 14]. Времена взаимодействий обращаются в пределе в ноль, а гипотеза удара переходит в гипотезу Ньютона для упругого взаимодействия.
При этом вид распределения Гиббса изменится. В представлении (23) исчезает член с большим параметром в показателе экспоненты и добавляются соотношения на границе и условия удара. В данном случае
(30)
$P({{q}_{{kq}}},{{p}_{{kq}}}) = Сехp\left[ { - \frac{{2b}}{S}Н({{q}_{{kq}}},{{p}_{{kq}}})} \right],\quad {{q}_{{kq}}} < \Delta ;\quad {{p}_{{kq}}}({{t}_{{0kq}}} - 0) = - {{p}_{{kq}}} + 0),$Распределение Максвелла (23) для случайных обобщенных импульсов сохраняет свой вид и удовлетворяет приведенным условиям упругого удара. Для анализа важны различного рода характеристики случайных импульсов ударов Jkq = 2 | pkq |. После вычислений, для многомерного случайного процесса пользуясь работами [8, 22] приходим к усеченному нормальному распределению для случайного процесса Jk
(31)
$~P({{J}_{{kqi}}}){\text{ }} = {{\left[ {\frac{{2b}}{{\pi S}}} \right]}^{{{\text{0}}{\text{.5}}N}}}\exp \left( { - \frac{{2b}}{S}\sum\limits_{k = 1}^{{{N}_{1}}} {\sum\limits_{q = 1}^{{{N}_{2}}} {J_{{kq}}^{2}} } } \right);\quad {{J}_{{kq}}} \geqslant 0,\quad N = {{N}_{1}}{{N}_{2}}.$Распределение (31) определяет силовые эффекты, связанные с влиянием ударов на динамику многомерной конструкции.
Для нечетных и четных j-х моментов одномерных величин Jkq можно, получить формулы [15, 19]
6. При рассмотрении случайных профилей в виброударных системах с большим числом степеней свободы одна из основных проблем состоит в определении частоты возникновения конфигураций, сопровождаемых взаимодействием тел, входящих в систему, с ограничителями.
Рассматривая случайные конфигурации, возникающие при реализации виброударных режимов в решетке, примем во внимание малую вероятность “запороговых” конфигураций (см. (29)). При $\lambda \to \infty $ из (24) и (30) найдем, после интегрирования по импульсам, распределение Больцмана
(32)
$w{\text{(}}{\mathbf{q}}_{{kq}}^{{}}{\text{)}} = {{C}_{{\text{2}}}}\exp \{ - 2b{{S}^{{ - {\text{1}}}}}{{U}_{{\text{*}}}}{\text{(}}{{q}_{{kq}}}{\text{)\} ;}}\quad {{U}_{{\text{*}}}}{\text{(}}{{q}_{{kq}}}{\text{)}} = \left[ {\frac{{\text{1}}}{{\text{2}}}c\sum\limits_{k = 1}^{{{N}_{1}}} {\sum\limits_{q = 1}^{{{N}_{2}}} {\sum\limits_{n = 1}^6 {D{}_{n}^{2}(q_{{kq}}^{{}})} } } } \right];\quad {{q}_{{kq}}} < \Delta ,$Получив представления (30) и (32), можно полностью описать “конфигурационные” характеристики системы: типы случайных профилей, их статистические характеристики и др.
Предположим, что есть возможность каким-то образом регистрировать любой случайно реализуемый профиль ${\mathbf{q}} = {\text{\{ }}q_{{kq}}^{{}}{\text{\} }}$. Зафиксируем его ${\mathbf{q}} = {{{\mathbf{q}}}^{{\text{0}}}}$ ≡ $\{ q_{{kq}}^{0}\} $ и определим среднюю частоту $({{\Omega }_{0}}\{ q_{{kq}}^{0}\} )$ его появления как математическое ожидание пересечения узлами решетки соответствующей поверхности в конфигурационном пространстве с положительной скоростью. Так как конфигурация $\{ q_{{kq}}^{0}\} $ – фиксирована, то фиксировано и значение потенциальной энергии ${{U}_{{\text{*}}}}(q_{{kq}}^{{\text{0}}})$ и, следовательно, можно найти
(33)
${{\Omega }_{0}}\{ q_{{kq}}^{0}\} = C\exp \left[ {\left( { - \frac{{2b}}{S}} \right){{U}_{{\text{*}}}}(q_{{kq}}^{{\text{0}}})} \right]\int\limits_0^\infty {...\int\limits_0^\infty {...\int\limits_0^\infty {\prod\limits_{k = 1}^{{{N}_{1}}} {\prod\limits_{q = 1}^{{{N}_{2}}} {{{p}_{{kq}}}} } } } } \exp \left[ {\left( { - \frac{{2b}}{S}} \right)\sum\limits_{k = 1}^{{{N}_{1}}} {\sum\limits_{q = 1}^{{{N}_{2}}} {p_{{kqi}}^{2}} } } \right]{\mathbf{dp}}{\text{ }}$Легко увидеть, что при функционировании рассматриваемой системы наиболее часто будет регистрироваться равновесная конфигурация ${{{\mathbf{q}}}^{{\text{0}}}} \equiv {\mathbf{0}}$.
Так как ${{U}_{{\text{*}}}}{\text{(}}{\mathbf{0}}{\text{)}} = {\text{0}}$, то после интегрирования из формулы (33) найдем
(34)
${{\Omega }_{0}}{\text{\{ }}{\mathbf{0}}{\text{\} }} = С{{\left( {\frac{S}{{16b}}} \right)}^{{{{N}_{1}}{{N}_{2}}}}}.$Из формул (33) и (34) найдем
(35)
${{\Omega }_{0}}{\text{\{ }}q_{{kq}}^{{}}{\text{(}}\Delta {\text{;}}\beta {\text{)\} }} = {{\Omega }_{0}}{\text{\{ }}{\mathbf{0}}{\text{\} }}\exp \left[ {\left( { - \frac{{2b}}{S}} \right){{U}_{{\text{*}}}}{\text{\{ }}q_{{kq}}^{{}}{\text{(}}\Delta {\text{;}}\beta {\text{)\} }}} \right].$(36)
${{{\omega }}_{{\beta }}}{\text{\{ }}q_{{kq}}^{{}}{\text{(}}\Delta {\text{;}}\beta {\text{)\} }} = {\text{exp}}\left[ {\left( { - \frac{{2b}}{S}} \right){{U}_{{\text{*}}}}{\text{\{ }}q_{{kq}}^{{}}{\text{(}}\Delta {\text{;}}\beta {\text{)\} }}} \right]$Итак, как и в других аналогичных случаях, относительно чаще смогут появляться профили, обладающие меньшей потенциальной энергией. Таким образом, чем меньше изломов присуще профилю, тем чаще он будет регистрироваться. Присутствие в формуле (36) экспоненты показывает, что рост потенциальной энергии профиля весьма быстро делает практически невозможной регистрацию каких-либо “экзотических” конфигураций с сильно изломанными профилями.
Рассматриваемые профили отвечают двум характерным значениям обобщенных координат:
нахождение в положении равновесия и достижение ограничителей: ${\mathbf{q}}{\text{(}}\Delta {\text{;}}\beta {\text{)}}$ = = 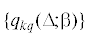 . Они, очевидно, достаточно характерны для данных типов решеток и их удобно регистрировать
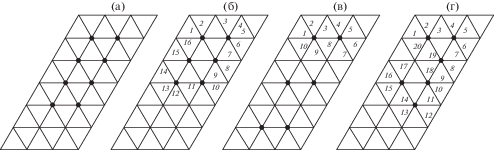
при помощи диаграмм показанных на рис. 5, где выбрана решетка в форме параллелограмма, имеющего 28 узлов, включая лежащие
на границе. Будем выделять узлы, находящиеся у ограничителя как показано на рис. 5а. В случае пребывания в состоянии равновесия выделять узел не будем. Таким образом
можно получить диаграммы, отвечающие рассматриваемым конфигурациям при помощи которых
можно оценить величины соответствующих значений потенциальной энергии, фигурирующей
в формуле (36).
. Они, очевидно, достаточно характерны для данных типов решеток и их удобно регистрировать
при помощи диаграмм показанных на рис. 5, где выбрана решетка в форме параллелограмма, имеющего 28 узлов, включая лежащие
на границе. Будем выделять узлы, находящиеся у ограничителя как показано на рис. 5а. В случае пребывания в состоянии равновесия выделять узел не будем. Таким образом
можно получить диаграммы, отвечающие рассматриваемым конфигурациям при помощи которых
можно оценить величины соответствующих значений потенциальной энергии, фигурирующей
в формуле (36).
Подробное описание возможных конфигураций для различных решеток можно провести методами комбинаторной геометрии [24], что представляет собой самостоятельную задачу. Для примера рис. 5 выберем конфигурации, отвечающие шести узлам, которые можно выбросить к ограничителю.
Наименьшее значение потенциальной энергии будет отвечать конфигурации с единственной выделенной точкой, так как в этом случае оказываются задействованными только шесть упругих соединений. В данном примере необходимо сравнивать конфигурации, в которых уровня ограничителя достигают шесть узлов, как это показано на рис. 5б,в,г.
Видно, что чем выше “кучность” соударяющихся узлов, тем меньше будет соответствующий уровень потенциальной энергии. Из диаграмм видно, что упругие элементы соседних взаимодействующих узлов не деформируются. Таким образом соседство двух выделенных или, наоборот, не выделенных узлов не увеличивает значение потенциальной энергии конфигурации. В то же время соседство выделенного и не выделенного узла увеличивает потенциальную энергию на величину ~$с{{\Delta }^{2}}$. Так что для конфигурации диаграммы b имеем 16 деформаций и ${{U}_{{\text{*}}}}$ ~ 16$с{{\Delta }^{2}}$, для диаграммы c – ${{U}_{{\text{*}}}}$ ~ ~ 30$с{{\Delta }^{2}}$, а для некоторой промежуточной конфигурации d – ${{U}_{{\text{*}}}}$ ~ 20$с{{\Delta }^{2}}$. Получается, что относительная частота появления конфигурации b – наиболее высока для комбинации с шестью соударяющимися узлами.
7. Приведем заключительные замечания.
7.1. Отмечено, что наименьшие значения потенциальной энергии имеют конфигурации, состоящие из единственного соударяющегося узла. Простые подсчеты показывают, что при рассмотрении профилей, в которых соударяются $Q \geqslant 2$ узлов, наименьшей потенциальной энергией обладают те, которые составляют выпуклый многоугольник. При $Q = 2$ многоугольник вырождается в отрезок.
7.2. Вместо неравенств (18) в рамках данной модели допустимо рассмотрение более сложной структуры конфигурационного пространства
(37)
$\begin{gathered} \Re = \{ {{\Delta }_{{{{2}_{{kq}}}}}} \leqslant {{q}_{{kq}}} \leqslant {{\Delta }_{{{{1}_{{kq}}}}}}\} ;\quad k = 0,\;...,\;{{N}_{1}};\quad q = 0,\;...,\;{{N}_{2}}; \\ - {\kern 1pt} \infty \leqslant {{\Delta }_{{{{2}_{{kq}}}}}} \leqslant 0;\quad 0 \leqslant {{\Delta }_{{{{1}_{{kq}}}}}} \leqslant \infty . \\ \end{gathered} $Это означает, что каждый узел может быть снабжен собственным ограничителем. При этом бесконечные значения отвечают случаю его отсутствия для данного узла (k, q). Распределения (30) и (31) – сохраняются, а для распределения (32) фазовые ограничения видоизменятся в соответствии с неравенствами (37). Структура формулы (36) сохранится.
7.3. При рассмотрении решеток с квадратными (прямоугольными) ячейками [8] все качественные выводы сохраняются. При рассмотрении одномерных цепочек [22] относительно часто регистрируемыми оказываются профили с одиночными, двойными, тройными и т.д. выбросами на ограничитель. При этом либо узел единственный, либо все узлы – лежат на одном отрезке. В этом – принципиальное отличие одномерной модели.
Рассмотренные модели могут быть использованы при рассмотрении двумерных дискретно-континуальных систем [22], а также при изучении самоподобных решетчатых структур [23].
7.4. Инженерное значение рассмотренных задач отмечено в п. 1. Они имеют не только модельную ценность, но и представляют интерес для инженеров-расчетчиков, так как открывают возможность получить определенные предварительные представления при выполнении динамических расчетов ряда конкретных двумерных конструкций, функционирующих в условиях соударения их элементов. В данном случае задачи усложняются и необходимо привлечение численных методов [24].
Информация о финансовой поддержке. Работа выполнена за счет гранта РНФ (проект № 19-19-00065).
Список литературы
Вибрации в технике. Справочник. Т. 4. Вибрационные процессы и машины / Под ред. Э.Э. Лавендела. М.: Машиностроение, 1981. 509 с.
Вайсберг Л.А, Картавый А.Н., Коровиков А.Н. Просеивающие поверхности грохотов. Screening media: конструкции, материалы, опыт применения. СПб.: ВСЕГЕИ, 2005. 250 с.
Нагаев Р.Ф., Ходжаев К.Ш. Колебания механических систем с периодической структурой // Ташкент: ФАН, 1973. 272 с.
Буров В.А., Волошинов В.Г., Дмитриев К.В., Поликарпова Н.В. Акустические волны в метаматериалах, кристаллах и структурах с аномальным преломлением // УФН. 2011. Т. 181. № 11. С. 1205–1211.
Bobrovnitskii Yu.I. Special issue on acoustic metamaterials // J. Acoust. Soc. Am. 2012. V. 132. № 4. Pt. 2. P. 2783–2945.
Бобровницкий Ю.И. Модели и общие волновые свойства двумерных акустических метаматериалов и сред // Акуст. журн. 2015. Т. 61. № 3. С. 283–294.
Асташев В.К., Крупенин В.Л. Нелинейная динамика ультразвуковых технологических процессов. М.: МГУП им. Ивана Федорова, 2016. 372 с.
Крупенин В.Л. Вибрационные и виброударные процессы в машинных конструкциях, собранных из решетчатых составляющих // Проблемы машиностроения и надежности машин. 2012. № 6. С. 11–18.
Крупенин В.Л. Анализ сингуляризированных уравнений движения решетчатых виброударных 2D-систем при отказе от гипотезы Ньютона // Проблемы машиностроения и надежности машин. 2016. № 2. С. 13–22.
Асташев В.К., Крупенин В.Л., Андрианов Н.А. Виброударные эффекты при ограниченных колебаниях струнных решеток с массивными узлами // ДАН. 2018. Т. 480. № 6. С. 1–5.
Никитенкова С.П., Потапов А.И. Акустические свойства двумерных фононных кристаллов с гексагональной симметрией // Вестник научно-технического развития. 2010. № 3 (31). С. 25–30.
Теоретическая механика. Упругие и тепловые свойства идеальных кристаллов. Учебное пособие / Беринский И.Е. и др. Под ред. А.М. Кривцова. СПб.: Изд-во Политехнич. ун-та, 2009. 143 с.
Александров П.С. Введение в общую теорию множеств и функций. М.-Л.: ОГИЗ, 1948. 413 с.
Крупенин В.Л. Расчет механизмов с пороговыми нелинейностями методом сингуляризации // Машиноведение. 1984. № 1. С. 6–12.
Babitsky V.I., Krupenin V.L. Vibration of Strongly Nonlinear Discontinuous Systems. Berlin: Springer-Verlag, 2001. 404 p.
Кляцкин В.И. Стохастические уравнения и волны в случайно-неоднородных средах. М.: Наука, 1980. 336 с.
Болотин В.В. Случайные колебания упругих систем. М.: Наука, 1979. 336 с.
Диментберг М.Ф. Нелинейные стохастические задачи механических колебаний. М.: Наука, 1980. 368 с.
Крупенин В.Л. Об исследованиях одномерных и многомерных виброударных процессов при случайном широкополосном возбуждении // Проблемы машиностроения и надежности машин. 2010. № 6. С. 25–31.
Федорюк М.В. Асимптотика: интегралы и ряды. M.: URSS. 2009. 544 с.
Gruber P. Convex and Discrete Geometry. Berlin: Springer-Verlag, 2007. 580 p.
Erofeev V.I., Pavlov I.S., Leontiev N.V. A Mathematical Model for Investigation of Nonlinear Wave Processes in a 2D Granular Medium Consisting of Spherical Particles // Composites: Mechanics, Computations, Applications, An International Journal. 2013. V. 4. № 3. P. 239–255.
Банах Л.Я. Колебания разветвленных самоподобных структур. Дихотомическая решетка // Проблемы машиностроения и автоматизации. 2014. № 1. С. 110–114.
Ганиев Р.Ф., Ревизников Д.Л., Сухарев Т.Ю., Украинский Л.Е. Оптимизация пространственного расположения рабочих элементов в установках колебательного типа // Проблемы машиностроения и автоматизации. 2018. № 1. С. 3–8.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин