Проблемы машиностроения и надежности машин, 2019, № 6, стр. 49-58

Статья посвящена дисперсионному уравнению колебаний свободной конечной упругой цилиндрической оболочки, погруженной в безграничную жидкость. Рассматриваемая задача находится на стыке теорий колебаний упругих цилиндрических оболочек и гидроакустики. Интерес к этой задаче вызван тем, что, несмотря на длительную историю исследований дисперсионных уравнений цилиндрических оболочек и их большую практическую значимость, она до сих пор была не решена.

Постановка задачи. Задана свободная конечная цилиндрическая оболочка (ниже для сокращения – оболочка), погруженная в жидкость, имеющая длину L и свободные края. Оболочка упругая тонкостенная. Внутри оболочки вакуум. Процессы на торцах не рассматриваются. Требуется определить дисперсионное уравнение свободных колебаний оболочки и его корни.

Исследованиям дисперсионного уравнения цилиндрических оболочек посвящен ряд работ отечественных и зарубежных авторов. В большей мере исследования проводились за рубежом, причем только для бесконечной оболочки. Имеет смысл ознакомиться с результатами этих исследований, чтобы лучше понять, в чем сходство и отличия дисперсионных уравнений конечных и бесконечных цилиндрических оболочек.

Зарубежные работы. Зарубежные исследования дисперсионного уравнения бесконечной цилиндрической оболочки имеют давнюю историю. В статьях [1, 2], на основе аналитического обзора множества американских и российских работ подведены итоги результатов исследований дисперсионных кривых для свободных колебаний бесконечной цилиндрической оболочки, погруженной в жидкость. Под дисперсионными кривыми понимаются графики функций корней дисперсионного уравнения от частоты колебаний.

Исследования выполнялись в течение примерно последних 60 лет. М. Юнгер [3] определил импеданс бесконечной цилиндрической оболочки в жидкости. М. Бэрон и Г. Блайх [4] описали модовый подход к вычислению частот и форм колебаний для бесконечной оболочки. П. Смит [5] идентифицировал три главных типа волн, которые существуют на цилиндрической оболочке, погруженной в жидкость. Г. Ворбертон [6] опубликовал обсуждение дисперсионных кривых цилиндрических оболочек, учитывающие эффекты жидкости, находящейся вне и внутри оболочки.

Дж. Скотт [7] показал, что некоторые публикации содержат ложные результаты.

В работе [1] рассмотрены дисперсионные кривые для бесконечной цилиндрической оболочки, погруженной в жидкость, и предложен алгоритм вычисления и визуализации дисперсионных кривых. Матричное уравнение движения цилиндрической оболочки основано на теории оболочек Флюгге в изложении Лейсса. Исходная формула перемещения оболочки w, названного свободной волной (надо полагать волной деформации), в явном виде не задана, но представлена в виде интеграла Фурье. Введен параметр κ = k_d/k – безразмерное осевое волновое число волны деформаций оболочки k_d, нормированное относительно акустического волнового числа среды (жидкости) k = ω/c. Относительно волнового числа k_d, (или κ = k_d/k), составляется и решается дисперсионное уравнение.

В этих работах дисперсионные уравнения цилиндрической оболочки в жидкости составлялись относительно волновых чисел волн изгибной деформации, бегущих по бесконечной оболочке.

Из отечественных работ отметим работы В.В. Болотина [8] и В.В. Музыченко [9]. В них рассматривались бесконечные оболочки. В работе [8] определялись собственные частоты при заданных волновых числах, бегущих по оболочке изгибных волн и критические скорости флаттера при обтекании оболочки потоком газа. В [9] рассматривалась оболочка в вакууме, так называемая “сухая” оболочка (не в жидкости).

Единственной отечественной работой, в которой было предложено приближенное дисперсионное уравнение для конечной цилиндрической оболочки в жидкости, является [10], в которой дисперсионное уравнение сводится к полиному высокого порядка относительно корней α_j, зависящему от числа взятых экспонент, аппроксимирующих излучаемое оболочкой звуковое поле. В результате решения дисперсионного уравнения число получаемых корней превышало восемь. Однако число определяемых корней α_j для конечной оболочки в жидкости должно быть восемь, j = 1, …, 8. Восемь фиксированных дискретных значений на каждой частоте колебаний по числу краевых условий (по четыре на каждом конце оболочки). Число краевых условий не зависит от отсутствия или наличия жидкости. В работе [10] не был предложен теоретически обоснованный алгоритм выбора восьми корней из большего числа полученных расчетом корней. По этой причине предложенная в [10] расчетная модель не приемлема.

Проведенный обзор опубликованных работ показал, что в теории колебаний цилиндрических оболочек в жидкости отсутствует решение задачи о колебаниях и излучении конечной цилиндрической оболочки в жидкости с учетом корней дисперсионного уравнения. Выяснилось, что дисперсионное уравнение для конечной оболочки в жидкости отсутствует, а дисперсионным уравнением для бесконечной оболочки воспользоваться нельзя.

Цель статьи – получить дисперсионное уравнение для конечной свободной цилиндрической оболочки в жидкости. Физический смысл задачи заключается в учете влияния звукового давления присоединенной жидкости на корни дисперсионного уравнения конечной цилиндрической оболочки и, следовательно, на частоты собственных колебаний цилиндрической оболочки в жидкости. Звуковое давление действует на внешнюю поверхность оболочки.

Уравнения свободных колебаний оболочки. Уравнения свободных колебаний конечной цилиндрической оболочки, основанные на моментной теории упругих оболочек Кирхгофа–Лява, имеют вид [11–13]

где $u,v$, w – осевые (продольные), окружные (тангенциальные) и радиальные перемещения оболочки; T₁, T₂, S, H, M₁, M₂ – упругие силовые факторы; q₁, q₂, q₃ – поверхностные нагрузки в направлениях $u,v$, w; a – радиус оболочки; h – толщина оболочки; ξ = x/a и φ – безразмерные координаты в осевом и окружном направлениях; t – время; ${{\rho }_{*}}$ – плотность материала оболочки; L – длина оболочки, 0 ≤ x ≤ L.

Решение уравнения свободных колебаний конечной цилиндрической оболочки (1) можно записать е [12, 13]

где n – окружные гармоники ряда Фурье, n = 0, 1, 2, 3, …, α_jn – корни дисперсионного уравнения, j = 1–8 – порядковые номера корней, С_jn – искомые коэффициенты, определяемые концевыми граничными условиями, $\Delta $_jn – миноры уравнения (1), представленного ниже в матричном виде, ω = 2πf – угловая частота колебаний,  f – частота колебаний. В решение (2) входят подлежащие определению корни дисперсионного уравнения α_jn и коэффициенты С_jn.

Для простоты ограничимся рассмотрением одной окружной гармоники n, опускаем e^iωt зависимость параметров от времени t, а также знаки суммирования по n и j, и сами индексы n и j там, где в них нет особой необходимости. Для определения корней α_jn решения (2) представим в виде [12]

Подставив решения (3) уравнение (1) получим уравнения свободных колебаний оболочки, которые могут быть представлены в матричном виде

где L_jk – элементы матрицы оболочки в вакууме, q = Eh/(1 – μ²)a – удельная жесткость, E – модуль упругости, h – толщина оболочки, μ – коэффициент Пуассона, p_s – звуковое давление, действующее на оболочку по радиальной координате w, вызываемое колебаниями оболочки в жидкости, q₁= q₂ = 0.

Элементы матрицы (4)

a₁, b₁ – параметры стрингеров; а₂, b₂, z₂ – параметры шпангоутов; E = E₀(1 + iη) – комплексный модуль упругости; η – потери в материале оболочки; r = a, i – мнимая единица.

Каждое из решений $u,v$, w (2) состоит из восьми слагаемых по числу концевых граничных условий оболочки. Соответственно числу слагаемых для каждой гармоники n и для каждой частоты колебаний ω надо определить восемь корней α_j, входящих в перемещения $u,v$, w. Физический смысл наличия в (4) давления q₃= p_s, влияющего на параметр α_jn, заключается в учете влияния присоединенной жидкости на собственные частоты и формы радиальных колебаний оболочки. При этом принято считать, что звуковое давление в жидкости, прилегающей к поверхности оболочки, действует на поверхность оболочки по направлению радиальных колебаний оболочки w.

Звуковое давление в жидкости. Переходим к главному вопросу – определению звукового давления p_s, которое должно быть перенесено в левую часть уравнения (4). Как известно, в формулах, определяющих излучение цилиндрической оболочки, должно быть задано распределение радиального перемещения поверхности оболочки по ее длине. Для определения давления на поверхности оболочки существуют формулы для плоской задачи [14]

где радиальное перемещение, распределенное по окружности

Для определения давления звукового поля, излучаемого колеблющейся цилиндрической оболочкой известны две формулы:

Первая из них формула, основанная на импедансе, приведенном E. Скучиком [15] со ссылкой на первоисточник M.C. Junger [3] для бесконечной оболочки, имеет вид

где w – радиальное перемещение поверхности оболочки; k = ω/c – волновое число звуковой волны в жидкости; ω = 2πf – угловая частота колебаний; c – скорость звука в жидкости; f – частота колебаний в Гц; k_x – осевое волновое число звуковой волны в жидкости; a – радиус оболочки; $H_{n}^{{(2)}}(a\tau )$, $H_{n}^{{(2){\kern 1pt} '}}(a\tau )$ – функция Ганкеля второго рода и ее производная; ρ₀ – плотность жидкости; r – радиальная координата точки определения давления.

В формуле (7) параметры w, k_x приведены без объяснений их физического смысла, хотя в первоисточнике [3] они определены. Обычно формула (7) применяется для бесконечной оболочки, в которой перемещение w = w(x) задается в виде изгибной волны деформации оболочки, распространяющейся вдоль оболочки, с заданным осевым волновым числом k_x [3].

Вторая формула – это формула расчета звукового излучения конечной цилиндрической оболочки при заданном произвольном распределении перемещения w(x) по ее образующей, допускающая его разложение в интеграл Фурье [14]

где γ – переменная интегрирования, имеющая смысл осевого волнового числа звуковой цилиндрической волны в жидкости, бегущей в направлении оси x.

При выводе формулы (8) произвольное перемещение было представлено в виде интеграла Фурье [2]

где x, z – разные обозначения одной и той же осевой координаты оболочки, записанные во избежание путаницы в показателях экспонент.

В работе [8] перемещения для бесконечной оболочки приняты в виде бегущей волны деформации

где k_d = 2π/λ – волновое число осевой изгибной волны деформации оболочки, λ – длина волны деформаций. Формула звукового давления при заданном радиальном перемещении w (10) имеет вид [8]

В работе [1] исходное звуковое давление жидкости на оболочку p(a, φ, ζ) представлено в виде формулы (8), в которой принято γ = k_d. Импедансы для бесконечных оболочек в работах [1, 3, 8] по сути одинаковые. Окончательные формулы звукового давления для бесконечной оболочки, используемые в дисперсионных уравнениях [1, 8] сводятся к виду (7), (11).

Для конечной оболочки в жидкости определим физико-математическую модель, т.е. физическую природу и математическое выражение дисперсионного уравнения. В качестве исходной формулы расчета звукового давления примем формулу (8). Сначала преобразуем формулу (8) для того, чтобы получить из нее импедансное выражение аналогичное (7), связывающее давление p с перемещением w. Следуя методу, примененному в [14], в формуле (8) заменим переменную интегрирования γ = cosα (при отсчете угла α от продольной оси оболочки) и представим ее в виде контурного интеграла

В результате вычисления интеграла (12) методом перевала находим точку перевала α = θ, где θ угол, определяющий направление на точку наблюдения. Следовательно, вычислять звуковое давление надо при γ = k cos θ. Подстановку γ = k cos θ делаем во всех элементах выражения (8), кроме членов, относящихся к собственно перемещению (9). Элементы выражения (8), появившиеся вследствие представления исходного перемещения w(z) в виде интеграла Фурье (9), заменим исходным выражением перемещения (9). В результате получим импедансное выражение, связывающее звуковое давление излучения p(x) и перемещение w(x) на поверхности конечного цилиндра

В формуле (13) функция Ганкеля описывает звуковую волну, излучаемую во внешнее пространство под углом θ к оси оболочки. Нам надо определить не звуковую волну, излучаемую оболочкой во внешнее пространство, а воздействие звукового давления на оболочку p_s (4), которое в качестве дополнительной нагрузки (дополнительной к удельной инерционной нагрузке от массы единицы длины оболочки) влияет на собственные колебания оболочки.

Определим эту дополнительную нагрузку. Уравнения колебаний оболочки (1), как всякой упругой системы с распределенными параметрами, составляются для выделенного элементарного участка оболочки, имеющего бесконечно малые размеры и расположенного между сечениями с продольными координатами x и x + dx, где x текущая координата. В решении w = w₀e^iαξ (3) параметр w это радиальное перемещение выделенного участка, расположенного в сечении текущей продольной координаты ξ = x/a.

В случае отсутствия жидкости, т.е. в случае “сухой” оболочки, корни α_jn в перемещении w = w₀e^iαξ (3) являются комплексными безразмерными параметрами, их численные значения определятся удельными инерционными и жесткостными параметрами оболочки, отнесенными к единице длины оболочки. Корни α_jn влияют на частоты собственных колебаний оболочки.

В случае оболочки, погруженной в жидкость, на оболочку действует дополнительное звуковое давление жидкости, содержащее функции Ганкеля, в аргументы которой входят осевые волновые числа γ (8). При этом ни физическая сущность корней α_jn, ни их число не изменяется. Вследствие влияния присоединенной жидкости изменяются численные значения корней “сухой” оболочки, что приводит к изменению частот собственных колебаний оболочки. Поскольку безразмерные корни α_jn не являются волновыми числами, имеющими размерность (1/м), они не могут выступать в роли осевых волновых чисел k_x. Другими словами, корни α_jn не могут присутствовать в аргументах функции Ганкеля в роли осевых волновых чисел.

Поскольку местоположение точки наблюдения в пространстве произвольное, то в формуле (13) параметры r и θ произвольные. Преобразуем формулу излучения (13) в формулу, определяющую действие акустического давления на оболочку. Определим параметры r и θ. Действие звукового давления на оболочку рассматриваем как нагрузку, локально действующую на выделенный элементарный участок оболочки в направлении радиального перемещения w (3), т.е. в направлении нормальном к поверхности оболочки. Считая, что реакция жидкости на колебания оболочки (звуковое давление), действующая на каждый текущий выделенный элементарный участок, направлена по нормали к элементарному участку оболочки, в формуле (13) примем r = a, и угол θ = = 90°. При таком выборе угла θ устраняется влияние его на корни α_jn и подтверждается прогнозируемый из физических соображений факт, что собственные колебания свободной конечной оболочки в жидкости не могут зависеть от угла θ.

В результате преобразования формулы звукового излучения оболочки (8), получаем формулу звукового давления, действующего как дополнительная нагрузка на поверхность конечной оболочки, совершающей собственные колебания

Формула (14) удовлетворяет изложенным выше физическим соображениям. Аргумент функции Ганкеля в (14) не содержит корней α_jn дисперсионного уравнения. Перемещения w(x) в левой и правой частях уравнения (4) одинаковые, что позволяет перенести давление (14) в левую часть уравнения (4) и получить дисперсионное уравнение свободных колебаний оболочки в жидкости. Формула (14), характеризующая реакцию жидкости на колебания оболочки, отличается от (13) не только написанием, но и физическим смыслом. Специфика давления по (14) в том, что это не звуковая волна, излучаемая оболочкой во внешнее пространство, а дополнительная распределенная нагрузка на конструкцию, влияющая на ее собственные колебания.

Сравним полученную формулу (14) с известными формулами. Сравнение формул реакции жидкости (звукового давления) для конечной (14) и бесконечной (11) оболочек показывает, что они имеют принципиальные различия в части аргумента функции Ганкеля. Формула (14) также отличается от формулы для плоской задачи (1), поскольку формула (1) получена для оболочки, не имеющей координаты длины x. Формула (1) вообще не для оболочки, она для поперечного сечения оболочки, в плоскости которого задано распределение перемещения по окружной координате φ. Переносить это выражение в левую часть уравнения колебаний (4) нельзя, т.к. в левой части уравнения записано перемещение в виде (3), содержащее осевую координату x.

Дисперсионное уравнение. Дисперсионное уравнение конечной оболочки в жидкости получим, перенеся звуковое давление (14), с учетом w = w(x) и p_s = p(x), в левую часть уравнения (4).

Предварительно уравнение (4) представим в краткой записи

Используя краткую запись

определим перемещения

Вернемся к третьему уравнению матричного уравнения (4)

Определив из (15) перемещения ($u,\;v,\;w$) и, выразив их через w, получим уравнение

где ∆⁽¹⁾ – минор, а ∆₀ – определитель матрицы (5),

Представим звуковое давление через импеданс Z, p_s = Zw, и, подставив его в (16), получим дисперсионное уравнение свободных колебаний оболочки в жидкости

В итоге, с учетом (17) дисперсионное уравнение для конечной цилиндрической оболочки, погруженной в жидкость, имеет вид

Решение дисперсионного уравнения (18), т.е. определение его корней, сводится к решению биквадратного полинома

Параметры полинома А₈–А₀ не выписаны из-за их громоздкости, обусловленной выражениями (5). В результате решения биквадратного полинома (19) получим четыре квадратных корня, после извлечения квадратов получим восемь комплексных корней, из них четыре корня положительных и четыре корня отрицательных, модули у соответствующих положительных и отрицательных корней одинаковые.

Проведенное исследование показывает, что дисперсионное уравнение конечной цилиндрической оболочки в жидкости (18) и его корни α_jn не зависят ни от длины оболочки, ни от осевых волновых чисел.

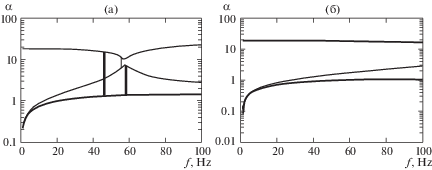
Пример расчета. В качестве примера, на рис. 1 приведены расчетные модули корней α дисперсионного уравнения конечной цилиндрической оболочки в жидкости в зависимости от частоты колебаний f (Гц): а) в жидкости; б) в вакууме. Исходные расчетные данные: Е = 2 × 10¹¹ H/м², ρ₀ = 10³ кг/м³, ${{\rho }_{*}}$ = 11 × 10³ кг/м³, с = 1500 м/с, n = 2, a = 4 м, h = 0.04 м, μ = 0.3.

На рис. 1а, б два верхних корня практически сливаются в один, самые нижние корни близки по числовым значениям, а промежуточные корни имеют существенные отличия, особенно в интервале частот  f  = 40–60 Гц. На рис. 1а видны вертикальные линии между кривыми, это условные фоновые линии, создаваемые графической программой Mathcad.

Из полученных данных следует, что корни дисперсионного уравнения для оболочки в жидкости могут существенно отличаться от корней оболочки в вакууме. Это различие может существенное влиять на амплитудно–частотные характеристики колебаний оболочек и резонансные частоты.

Заключение. Получено дисперсионное уравнение (18) для конечной цилиндрической оболочки, погруженной в жидкость, учитывающее влияние жидкости на собственные колебания оболочки. Уравнение получено на основе физико-математической модели, включающей: 1) теорию цилиндрических оболочек Кирхгофа–Лява (1), используемую для получения уравнения движения оболочки; 2) формулу звукового давления (8), излучаемого конечной цилиндрической оболочкой в жидкости, преобразованную путем математически и физически обоснованного перехода к давлению, действующему на оболочку в условиях собственных колебаний оболочки (14).

Решения, выражаемые формулами (14) и (18), это новые решения в области виброакустики цилиндрических оболочек. Полезность их обусловлена тем, что корни α_jn дисперсионного уравнения необходимы для проведения всех последующих гидроакустических расчетов цилиндрических оболочек. Они используются в расчетах собственных и вынужденных колебаний реальных составных оболочечных конструкций и излучаемых ими гидроакустических полей [16].