Проблемы машиностроения и надежности машин, 2019, № 6, стр. 42-48

Введение. Особенностью механизмов относительного манипулирования является наличие двух выходных звеньев [1]. Функционирование механизмов относительного манипулирования аналогично действию двух рук человека [2].

Это позволяет получить в относительном движении выходных звеньев большее число степеней свободы, чем у составляющих модулей и реализовать более сложные операции, не реализуемые однорукими системами.

Механизм относительного манипулирования является основой технологических обрабатывающих систем, автооператоров станков и двуруких роботов. Структурный синтез механизмов относительного манипулирования рассматривается в работе [2]. Особенности построения движений двуруких роботов и алгоритм управления рассматривается в работе [3, 4].

1. Обратные задачи относительного манипулирования. Обратной задачей относительного манипулирования будем называть задачу определения обобщенных координат механизма относительного манипулирования, при которых реализуется заданное относительное положение выходных звеньев или их элементов. Такими элементами могут быть точка, плоскость, прямая или все твердое тело. Рассмотрим обратные задачи относительного манипулирования для механизмов с тремя степенями свободы, решение которых позволяет реализовать заданные относительные движения точки.

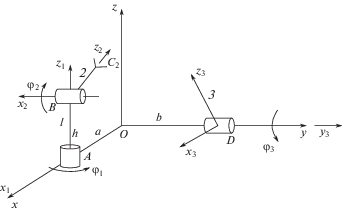
1.1. Механизм В₃В₁-В₂. Первый модуль В₃В₁ содержит две вращательные кинематические пары, одна из которых параллельна оси Oz неподвижной системы координат, а ось второй пары в начальном положении параллельна оси Ox (рис. 1).

Второй модуль В₂ содержит одну вращательную пару, ось которой параллельна оси Oy.

Механизм имеет три степени свободы. Обобщенными координатами являются углы относительного поворота звеньев φ₁, φ₂, φ₃. Механизм позволяет осуществить заданное относительное движение точки выходного звена одного модуля в системе координат выходного звена второго модуля.

Будем считать, что заданы координаты программного движения точки в системе координат модуля В₂ и требуется осуществить совпадение точки выходного звена модуля В₃В₁ с этой точкой путем совместного движения по обобщенным координатам обоих модулей φ₁, φ₂, φ₃. Задача состоит в определении величин φ₁, φ₂, φ₃ при заданных координатах точки в системе модуля B₂.

Для решения задачи со звеньями механизма свяжем системы координат следующим образом: 1) со звеном 1 свяжем систему координат Ax₁, y₁, z₁, направив ось z₁ по оси вращательной пары А; 2) со звеном 2 свяжем систему координат Bx₂, y₂, z₂, направив ось z₂ по оси звена 2, а ось x₂ по оси вращательной пары B; 3) со звеном 3 свяжем систему координат Dx₃, y₃, z₃, направив ось y₃ по оси вращательной пары D. Эта система повернута вокруг оси Oy на угол φ₃.

Система координат Bx₂, y₂, z₂, может быть совмещена с системой Ox,y,z путем поворота вокруг оси x₂ на угол φ₂, переносом по оси z₁ на величину h, поворотом вокруг оси z₁ на угол φ₁ и переносом по оси x на величину а.

Матрицы поворотов третьего порядка систем, связанных со звеньями 1 и 2 имеют вид

Координаты точки С₂ звена 2 в неподвижные системы координат равны

Для реализации заданного движения точка С₂ звена 2 должны совпасть с заданной точкой С₃ звена 3. Координаты точки С₃ считаем задаными в подвижной системе координат второго модуля Dx₃, y₃, z₃

Найдем значения обобщенных координат φ₁, φ₂, φ₃ обоих модулей, при которых точка С₂ первого модуля совмещается с точкой C₃ второго модуля с заданными координатами. В неподвижной системе координат для точки С₃ получим

где ${{r}_{3}} = {{\left( {z_{3}^{2} + x_{3}^{2}} \right)}^{{0.5}}}$.

Приравняем (1) и (2) получим систему уравнений для определения φ₁, φ₂, φ₃

Возведя в квадрат и складывая уравнения, получим

С помощью замены sinφ₃ и cosφ₃ через тангенс половинного угла φ₃ из последнего уравнения получим квадратное уравнение для определения ${\text{tg}}\left( {\frac{{{{{\varphi }}_{3}}}}{2}} \right)$

где ${{a}_{1}} = 2a{{r}_{3}}$; ${{b}_{1}} = 2h{{r}_{3}}$; ${{c}_{1}} = r_{3}^{2} + {{a}^{2}} + {{h}^{2}} - l_{2}^{2} + {{y}^{2}}$, откуда

Из третьего уравнения системы (3) получим

Из второго уравнения системы (3) получим

Формулы (4), (5), (6) позволяют определить переменные управляющих функций и выбрать постоянные параметры механизма, позволяющие реализовать заданные условия движения.

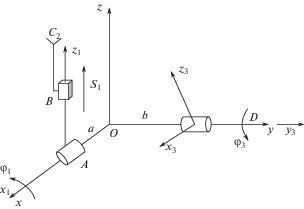
1.2. Механизм В₁П₃-В₂. Механизм содержит два модуля, один модуль содержит вращательную и поступательную пару, второй содержит одну вращательную пару.

Второй модуль содержит одну вращательную пару и совершает вращательное движение вокруг оси y. Со звеньями механизма 1 и 3 свяжем декартовы системы координат, как показано на рис. 2. Со звеном 2 свяжем систему координат С₂x₂y₂z₂, которая смещена относительно системы Аx₁y₁z₁ на величину s₂ по оси Оz₁, а оси Сx₂ и Сy₂ параллельны соответствующим осям Ax₁ и Az₁.

Определению подлежат обобщенные координаты φ₁, s₂, φ₃. Параметры: a, b – постоянные. Координаты точки С₂ звена 2 в неподвижной системе координат равны

Координаты точки С₃, с которой совпадает точка С₂ в системе Dx₃, y₃, z₃ считаем заданным

Координаты точки С₃ в неподвижной системе координат равны

Приравнивая координаты точек С₂ и С₃ в неподвижной системе координат получим

Из полученных уравнений находим выражения обобщающих координат, которые являются управляющими функциями

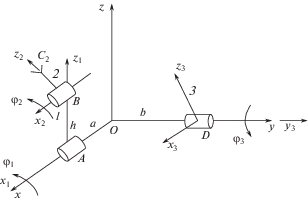
1.3. Механизм В₁В₁-В₃. Механизм содержит два модуля: 1) один модуль содержит две вращающиеся пары, оси которых параллельны; 2) второй модуль содержит одну вращательную пару и совершает вращательное движение.

Со звеньями 1, 2 и 3 свяжем системы координат Ax₁, y₁, z₁ и Вx₂, y₂, z₂, Dx₃, y₃, z₃ как показано на рис. 3. Обобщенными координатами механизма являются углы относительных поворотов звеньев φ₁, φ₂, φ₃.

Координаты точки C₂ в неподвижной системе координат равны

где ${\alpha } = {{{\varphi }}_{1}} + {{{\varphi }}_{2}}$.

Координаты точки контакта С₃ в подвижной системе координат Dx₃,y₃,z₃ считаем заданным

Координаты точки С₃ в неподвижной системе координат равны

При совпадении точек С₂ и С₃ их координаты совпадают и в неподвижной системе координат, приравнивая координаты получим

Возведя в квадрат и складывая эти уравнения получим

откуда

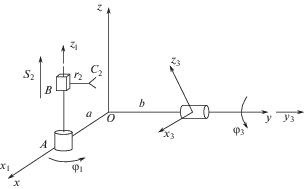
1.4. Механизм В₃П₃-В₂. Механизм содержит два модуля: 1) один модуль содержит одну вращательную и одну поступательную кинематические пары; 2) второй модуль совершает вращательное движение (рис. 4).

Обобщенные координаты механизма φ₁, s₂, φ₃. Координаты точки контакта С₃ в подвижной системе координат Dx₃, y₃, z₃ считаем заданным

Координаты точки С₂ звена 2 в неподвижной системе равны

Координаты точки C₃ звена 3 в неподвижной системе координат равны

Приравнивая (7) и (8) получим

откуда где ${{r}_{3}} = \sqrt {x_{3}^{2} + z_{3}^{2}} $.

2. Осуществление перехода механизма из одного относительного положения в другое. Имея начальное и конечное значения обобщенных координат модулей механизма относительного манипулирования, можно построить процесс перехода его из начального положения в конечное.

Используем для этого синусоидальный закон изменения обобщенного ускорения $\ddot {q}$

где $\Delta q$ – разность между начальным и конечным значениями координат; ${{\dot {q}}_{{{\text{max}}}}}$ – максимальная обобщенная скорость.

Закон изменения обобщенной скорости находится путем интегрирования выражения (9)

Закон изменения обобщенных координат механизма находится путем интегрирования (10)

Максимальную обобщенную скорость принимаем исходя из назначения механизма.

Максимальное обобщенное ускорение зависит от максимальной скорости и величины перемещения и определяется из (9)

Время перехода из начального положения в конечное можно получить из (11)

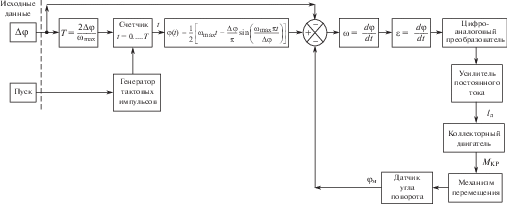
Полученные соотношения позволяют построить структуру системы управления по обобщенным координатам механизма рис. 5.

Выводы. 1) получены решения обратных задач относительного положения манипуляторов с двумя степенями свободы и модулей поступательного и вращательного движений; 2) решения позволяют реализовать заданные относительные движения выходного звена манипулятора и подвижных деталей путем управления переменными параметрами систем; 3) полученные соотношения позволяют так же выбирать постоянные параметры автооператоров станков и двуруких роботов.