Проблемы машиностроения и надежности машин, 2019, № 7, стр. 64-71

Введение. Ветроэнергетика является одним из основных направлений альтернативной энергетики, в основе которой кинетическая энергия воздушных масс атмосферы преобразуется в электрическую, механическую или тепловую энергии. Для преобразования энергии воздушного потока в электрическую обычно используются ветряные турбины. В последнее время активно исследуется возможность генерирования электрической энергии с помощью ветрового генератора, который в англоязычной литературе называют “Windbelt” [1–8].

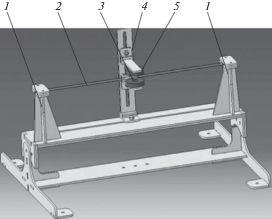
Принципиальная схема устройства показана на рис. 1 [4]. На гибкой ленте 2, натянутой между двумя жесткими опорами 1, закреплен постоянный магнит 3 (известны конструкции с двумя и более магнитами [5]). Соосно с магнитом сверху и снизу ленты на раме 4 установлены индуктивные катушки 5. При определенных условиях воздушный поток может нарушить статическое равновесие ленты и привести к возбуждению ее колебаний по типу аэроупругого флаттера [9]. Колебательное движение магнита индуцирует возникновение переменного электрического тока в индуктивных катушках, который может выпрямляться в постоянное напряжение.

В научной литературе имеются исследования, связанные с генерацией электрического тока в подобных устройствах. Вместе с тем, вопросы, связанные с исследованиями колебаний тонкой ленты в зависимости от ее натяжения и скорости набегающего потока изучены недостаточно подробно. Известные расчетные модели основаны на различных упрощающих допущениях, ограничивающие исследование закритического поведения ленты.

Целью данной статьи является моделирование динамики ленты в воздушном потоке, анализ ее движения и возможность оптимизации конструкции.

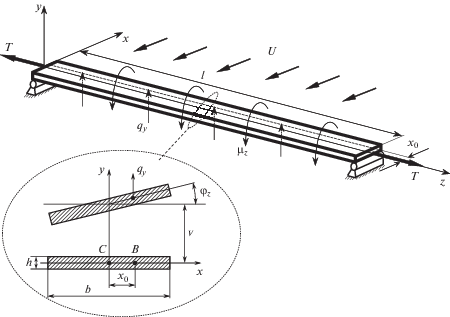
Постановка задачи. Шарнирно закрепленная лента длиной l находится в набегающем потоке воздуха (рис. 2). Поперечное сечение ленты постоянно по длине. Лента вдоль оси Oz растянута продольной силой T. При действии на ленту горизонтального поперечного потока воздуха (ветровой нагрузки) с постоянной скоростью U, возникает подъемная сила ${{q}_{y}}$. Ветровая нагрузка равномерно распределена по длине.

Считаем, что равнодействующая подъемной силы приложена по линии, проходящей через центры давления поперечных сечений ленты, параллельной оси Oz и расположенной от нее на расстоянии x₀ (рис. 2).

В каждом текущем сечении ленты действует погонная подъемная сила ${{q}_{y}}$, которая приложена в центре давления (точка B на рис. 2) [9]

где $\rho $ – плотность среды (плотность воздуха); $b$ – ширина поперечного сечения ленты; ${{C}_{y}}$ – коэффициент подъемной силы.

Приведем подъемную силу (1) к центру поперечного сечения C. Т.к. линия расположения центров давления не совпадает с центральной осью поперечного сечения ленты, дополним систему действующих сил погонным крутящим моментом

здесь принято, что центр давления подъемной силы находится на расстоянии ${{x}_{0}} = b{\text{/}}4$ хорды от центра тяжести ленты.

Коэффициент подъемной силы ${{C}_{y}}$ для тонкого прямоугольного профиля ленты задается нелинейным аналитическим выражением, вычисленным через обратное конформное отображение известного решения для обтекания кругового цилиндра потоком идеальной несжимаемой жидкости на внешность отрезка

где ${{\tilde {\varphi }}_{z}}$ – эффективный угол атаки, который представляет собой разность геометрического угла атаки ${{\varphi }_{z}}$ и его динамической составляющей, и определяется по формуле где $v$ – вертикальное перемещение оси ленты (полюса).

Раскладывая выражение (3) в ряд Тейлора и, ограничиваясь первыми двумя членами ряда, получим

где ${{A}_{1}} = 2\pi ,{{A}_{3}} = 2\pi {\text{/}}6$ – коэффициенты разложения.

Уравнения движения. Движение расчетной модели описывается системой уравнений поперечно-крутильных колебаний для шарнирно-опертой струны, нагруженной распределенной силой и распределенным моментом. С учетом выражений (1) и (2) для распределенных аэродинамических сил и выражения (4) для коэффициента подъемной силы система уравнений, описывающих поперечно-крутильные колебания ленты, примет вид

где ${{\rho }_{1}}$ – плотность материала ленты; $G$ – модуль сдвига; $A = bh$ – площадь поперечного сечения; ${{I}_{0}} = bh({{b}^{2}} + {{h}^{2}}){\text{/}}12$ – полярный момент инерции; ${{I}_{k}} = b{{h}^{3}}{\text{/}}3$ – геометрическая жесткость сечения (полосы) при кручении; ${{d}_{v}}$, ${{d}_{\varphi }}$ – коэффициенты линейно-вязкого демпфирования по Рэлею при изгибе и кручении, соответственно.

Приведем систему (5) к безразмерному виду, используя безразмерные переменные: время $\tau = t{\text{/}}{{t}^{*}}$, прогиб $\xi = v{\text{/}}{{V}^{*}}$, угол $\varphi = {{\varphi }_{z}}{\text{/}}2\pi $, координата $\zeta = z{\text{/}}{{Z}^{*}}$, скорость $\Lambda = U{\text{/}}{{U}^{*}}$ и сила $\theta = T{\text{/}}{{T}^{*}}$, где масштабы ${{t}^{*}} = l{\text{/}}h\sqrt {{{\rho }_{1}}({{b}^{2}} + {{h}^{2}}){\text{/}}4G} $; U* = $\sqrt {8G{{h}^{3}}{\text{/}}(3{{\rho }_{0}}{{a}_{0}}b{{l}^{2}})} ;$ ${{V}^{*}} = h;$ ${{Z}^{*}} = l;$ $T* = G{{h}^{2}}$.

Тогда система уравнений (5) запишется в виде

где ${{\alpha }_{1}},\,\,{{\beta }_{1}},\,\,{{\gamma }_{1}},\,\,{{\eta }_{1}},\,\,{{\gamma }_{2}},\,\,{{\eta }_{2}},\,\,{{d}_{\xi }},\,\,{{d}_{\varphi }}$ – безразмерные комплексы, определяемые по соотношениям (7). Все они выражаются через два фиксированных безразмерных параметра $\varepsilon = h{\text{/}}b$ и $\kappa = \sqrt {\rho {\text{/}}{{\rho }_{1}}} $.

Здесь коэффициенты демпфирования приняты равными 0.05 от соответствующего критического значения (k – номер гармоники). Приведение уравнений движений ленты (5) к безразмерному виду (6) позволяет сократить число параметров до четырех: $\varepsilon ,\kappa ,\Lambda ,\theta $, из которых только $\Lambda $ и $\theta $ являются определяющими.

Расчет критической скорости. Для анализа работы Windbelt System необходимо исследовать закритическое поведение устройства. С этой целью зафиксируем критическое значение управляющего параметра безразмерной скорости воздушного потока ${{\Lambda }_{*}}$, при котором происходит потеря устойчивости (достигается режим флаттера).

Методом Галеркина система уравнений (6) сводится к системе с конечным числом степеней свободы. Решение представим в виде разложения по координатным функциям ${{u}_{k}}(\zeta )$

где ${{u}_{k}}(\zeta ) = {{C}_{k}} \cdot \sin (k\pi \zeta )$ выделенный ряд функций, удовлетворяющий граничным условиям для принятой расчетной модели (рис. 2). Константа ${{C}_{k}}$ определяется из условия ортонормированности функций ${{u}_{k}}(\zeta )$

После применения метода Галеркина система (6) примет вид

где ${{С}_{3}} = \int_0^1 {u_{k}^{4}d\zeta } $.

Существующее тривиальное решение системы (8), соответствует положению равновесия, которое рассматривается как невозмущенное движение. Для исследования на устойчивость система (8) линеаризуется около положения равновесия [10]

Система (9) в матричной форме имеет вид

где ${\mathbf{x}} = \left\{ \begin{gathered} {{p}_{k}} \hfill \\ {{q}_{k}} \hfill \\ \end{gathered} \right\}$; ${\mathbf{M}} = \left[ \begin{gathered} \begin{array}{*{20}{c}} 1&0 \end{array} \hfill \\ \begin{array}{*{20}{c}} 0&1 \end{array} \hfill \\ \end{gathered} \right]$, ${\mathbf{D}} = \left[ \begin{gathered} \begin{array}{*{20}{c}} {{{d}_{\xi }} + \Lambda {{\eta }_{1}}}&{\Lambda {{\gamma }_{1}}} \end{array} \hfill \\ \begin{array}{*{20}{c}} {\Lambda {{\eta }_{2}}}&{{{d}_{\varphi }} + \Lambda {{\gamma }_{2}}} \end{array} \hfill \\ \end{gathered} \right]$; ${\mathbf{C}} = \left[ {\begin{array}{*{20}{c}} {\theta {{\alpha }_{1}}{{\pi }^{2}}{{k}^{2}}}&{ - {{\Lambda }^{2}}{{\beta }_{1}}} \\ 0&{{{\pi }^{2}}{{k}^{2}} - {{\Lambda }^{2}}} \end{array}} \right]$.

Решения системы (10) находим в виде ${\mathbf{x}} = {{e}^{{\lambda \tau }}}{\mathbf{u}}$. Тогда характеристическое уравнение для определения $\lambda $ примет вид

В дальнейшем решение будем рассматривать только для первой гармоники ($k = 1$).

Важно подчеркнуть, что динамическая потеря устойчивости должна происходить раньше потери статической устойчивости. В противоположном случае будет наблюдаться явление дивергенции, при котором произойдет полная утрата жесткости ленты на кручение. Соответствующее условие определяется силой натяжения ленты $\theta $.

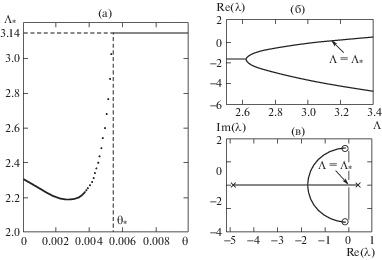
На рис. 3a представлена зависимость критической скорости ${{\Lambda }_{*}}$ от безразмерной силы натяжения $\theta $ при фиксированных значениях параметров $\varepsilon = 0.002,$ $\kappa = 0.03$. График наглядно показывает, что при достижении определенного значения силы натяжения $\theta = {{\theta }_{*}}$, критическая скорость достигает значения, равного $\pi $, и с дальнейшим увеличением $\theta $ перестает расти. Такое значение критической скорости ${{\Lambda }_{*}}$ соответствует дивергенции. Это подтверждается рис. 3б, в, где $\theta > {{\theta }_{*}}$. На рис. 3б верхняя ветвь траектории пересекает ось $\operatorname{Re} \left( \lambda \right) = 0$ при значении ${{\Lambda }_{*}} = \pi $, что соответствует переходу этой же траектории на графике Аргана (рис. 3в) через точку начала координат, т.е. сначала происходит статическая потеря устойчивости. На рис. 3в кружочками отмечено начало траекторий, а крестиками – их конец. Анализ полученных результатов показывает, что для потери динамической устойчивости раньше, чем потеря статической устойчивости параметр $\theta $ должен находиться в промежутке $(0,{{\theta }_{*}})$. В настоящей статье принято, что $\theta = 0.002$.

На рис. 4a представлены графики траекторий корней $\lambda $, вычисленные при выбранных значениях параметров $\kappa = 0.03,$ $\varepsilon = 0.002,$ $\theta = 0.002$; кружочками обозначено начало траекторий, а крестиками – их конец. Точка перехода графиков на правую полуплоскость характеризует критическое значение параметра скорости ${{\Lambda }_{*}} = 2.487.$ Величина мнимой части имеет смысл частоты колебаний ${{\omega }_{f}}$ системы при $\Lambda = {{\Lambda }_{*}}$. Значение ${{\omega }_{f}}$ отображается значением ординаты, указанной на рис. 4a.

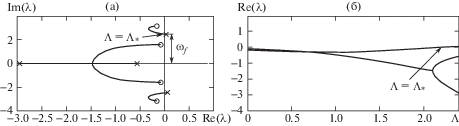
Само значение ${{\Lambda }_{*}}$ определяется по графику зависимости действительной части корней $\operatorname{Re} \left( \lambda \right)$ от $\Lambda $ (рис. 4б) в момент пересечения ее значения $\operatorname{Re} \left( \lambda \right) = 0$: ${{\Lambda }_{*}} = 2.203$.

Анализ закритического поведения. Для изучения закритического поведения интегрируется система с нелинейными слагаемыми (8) при $\Lambda $ большей ${{\Lambda }_{*}}$ на 10% и на безразмерном промежутке времени $\tau = 30 \cdot {{T}_{f}}$, где ${{T}_{f}} = 1{\text{/}}{{\omega }_{f}}$ – период колебаний для частоты ${{\omega }_{f}}$.

Численное моделирование уравнений (8) показывает, что устанавливаются периодические решения, т.е. в закритической области имеется неустойчивое положение равновесия и существуют устойчивые периодические движения, что соответствует поведению автоколебательной системы.

На рис. 5a, б приведены фазовые портреты решений уравнений (8) для вертикального безразмерного перемещения $\xi (\tau )$ сечения $\zeta = 0.5$ и его угла поворота $\varphi (\tau )$ при двух различных начальных условиях:

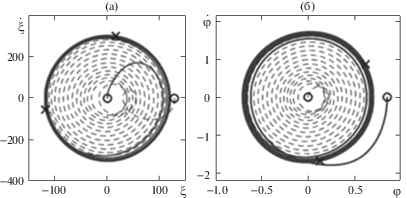
По графикам отчетливо видно притяжение траекторий к предельным циклам (сплошные линии соответствуют начальным условиям 1, штриховые – условиям 2, кружками обозначено начало траектории, а крестиками – их конец).

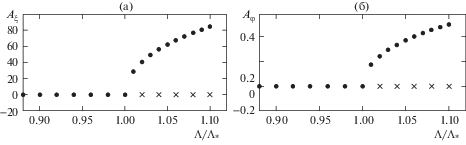
Построение бифуркационной диаграммы. Проведенный анализ устойчивости равновесного прямолинейного положения ленты позволяет построить бифуркационную диаграмму. На рис. 6 показаны бифуркационные диаграммы для амплитуд ${{А}_{\xi }}$ и ${{А}_{\varphi }}$, построенные численным интегрированием с помощью метода установления [11], где точками обозначены устойчивые движения, а крестиками – неустойчивые движения.

Заключение. В статье проанализированы малые изгибно-крутильные колебания гибкой ленты под действием набегающего потока воздуха, которые в упрощенном виде описывают динамику ветрогенератора типа “Windbelt”. Изгибно-крутильные колебания ленты описываются системой дифференциальных уравнений в частных производных, в которых нелинейность задается коэффициентом подъемной силы для тонкой пластинки, аналитически вычисленным через обратное конформное отображение известного решения для обтекания кругового цилиндра потоком идеальной несжимаемой жидкости.

В результате выполненных расчетов получены значения критической скорости, реализации движений и бифуркационные диаграммы. Показано, что в закритической области имеются устойчивые периодические движения с амплитудами, пропорциональными квадратному корню из параметра закритичности ${{A}_{{\xi ,\varphi }}} \sim \sqrt {\Lambda - {{\Lambda }_{*}}} $.

Полученные решения позволяют осуществлять рациональный выбор параметров Windbelt System, работающих в определенном диапазоне скоростей ветрового потока.

Финансирование работы. Работа выполнена при финансовой поддержке Российского научного фонда (проект № 18-19-00708).

Конфликт интересов. Авторы заявляют, что у них нет конфликта интересов.