Проблемы машиностроения и надежности машин, 2019, № 7, стр. 88-96
НЕЛИНЕЙНЫЙ АНАЛИЗ ВИБРОИЗОЛЯЦИИ ГРУЗА, УСТАНОВЛЕННОГО В КОНТЕЙНЕРЕ НА ПОЛИУРЕТАНОВЫХ АМОРТИЗАТОРАХ ТОННЕЛЬНОГО ТИПА
А. Е. Белкин 1, *, И. З. Даштиев 2, **, Е. А. Никитин 1, ***
1 Московский государственный технический университет им. Н.Э. Баумана
г. Москва, Россия
2 Центральный научно-исследовательский институт специального машиностроения,
Московская область
г. Хотьково, Россия
* E-mail: aefbelkin@gmail.com
** E-mail: koleso49@mail.ru
*** E-mail: devoitene@gmail.com
Поступила в редакцию 10.07.2019
Принята к публикации 26.08.2019
Аннотация
Исследуется виброизоляция груза в контейнере с применением полиуретановых амортизаторов тоннельного типа, допускающих работу при больших деформациях и обладающих высокими коэффициентами поглощения энергии. Для выполнения расчетов проведена аппроксимация упругой и диссипативной характеристик амортизаторов по результатам их статических и динамических испытаний. Приближенными методами нелинейной теории колебаний рассчитаны модели систем поперечной и продольной амортизации груза с симметричной и несимметричной характеристиками. Для гармонического возбуждения определены коэффициенты виброизоляции груза, соответствующие различным амплитудам ускорения контейнера. Результаты расчетов сопоставлены с данными испытаний физической модели системы виброизоляции, полученными на вибростенде Data Physics Signal Force V400.
Введение. В современном машиностроении широко применяются детали из полиуретана, в частности амортизаторы, которые обладают высокой удельной энергоемкостью, весьма большими коэффициентами поглощения энергии и превосходят резиновые аналоги по долговечности [1, 2]. Благодаря технологичности изготовления амортизаторы могут иметь разнообразную геометрию, выбор которой влияет на их нагрузочные характеристики.
Для обеспечения вибро-удароизоляции грузов весьма перспективно применение амортизаторов тоннельного типа (рис. 1), которые могут работать при больших осадках, сопоставимых с высотами. Нагрузочные характеристики этих амортизаторов в диапазоне рабочих осадок нелинейны, причем в области малых деформаций характеристики являются мягкими с переходом к протяженному почти линейному участку малой жесткости, а после достижения некоторой осадки становятся жесткими из-за самоконтакта стенок. Амортизаторы с характеристиками такого вида обеспечивают высокую энергоемкость виброзащитной системы при ограниченных силах, передаваемых на защищаемый объект.
Для обоснования работоспособности полиуретановых амортизаторов в системах защиты объектов необходимы тщательные теоретические и экспериментальные исследования. Одно из первых экспериментальных исследований статических и динамических характеристик тоннельных амортизаторов проведено в работе [3]. Приближенный расчет близкого по характеристикам разрезного амортизатора с упорами на основе структурной вязкоупругой модели предложен в [4]. В работе [5] представлены результаты стендовых ударных испытаний тоннельного амортизатора и выполнено их математическое моделирование методом конечных элементов. В [6] экспериментально исследована простейшая физическая модель одноосной виброизоляции груза в контейнере с помощью двух полиуретановых амортизаторов тоннельного типа, являющихся малоразмерными копиями натурных амортизаторов. Испытания модели проводились на вибростенде Data Physics Signal Force V400.
На рис. 2 показана общая схема экспериментальной установки. Были получены амплитудно-частотные характеристики системы “контейнер–амортизаторы–груз” в виде зависимости коэффициента динамичности от частоты возбуждения с заданной амплитудой ускорения контейнера (стола вибростенда). По результатам испытаний проведена настройка математической модели как одностепенной системы с кинематическим возбуждением, в которой реакции амортизаторов определялись соотношениями линейной теории вязкоупругости. Анализ этой модели позволил получить приближенную оценку уровня виброизоляции груза. Более точный анализ возможен с применением нелинейной теории.
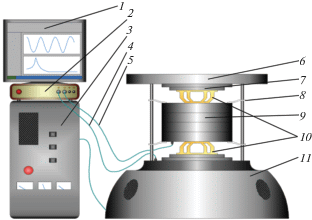
Рис. 2.
Схема экспериментальной установки физического моделирования амортизации груза в контейнере: 1 – монитор; 2 – система управления вибростендом; 3 – усилитель управляющего сигнала; 4, 5 – акселерометры стола и груза; 6 – верхний стол; 7 – крепление амортизатора; 8 – система стабилизации; 9 – груз; 10 – амортизаторы; 11 – вибростенд.
Цель настоящей статьи – разработка математической модели нелинейной системы виброизоляции груза на полиуретановых амортизаторах при колебаниях с большими амплитудами и настройка этой модели по результатам экспериментов.
Аппроксимация силовой характеристики системы виброизоляции. Выберем аналитическое представление восстанавливающей силы $f$ от осадки амортизатора $\delta $. Приближенно $f$ можно представить в виде суммы упругой ${{f}_{e}}(\delta )$ и неупругой ${{f}_{i}}(\delta ,\dot {\delta })$ составляющих [7]
В соответствии с видом нагрузочной характеристики амортизатора (рис. 3), а также условиями установки амортизаторов в контейнере примем
(1)
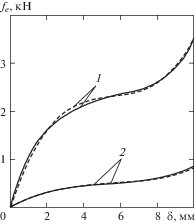
${{f}_{e}}(\delta ) = {{c}_{1}}\delta - {{c}_{2}}{{\delta }^{2}}\operatorname{sign} \delta + {{c}_{3}}{{\delta }^{3}},$Рис. 3.
Сравнение экспериментальных (штриховые кривые) и аналитических (сплошные кривые) упругих характеристик “жесткого” (1) и “мягкого” (2) амортизаторов.
Неупругая часть восстанавливающей силы отражает способность амортизаторов рассеивать механическую энергию благодаря значительному внутреннему трению в материале. Известно [8], что площадь гистерезисной петли у эластомеров в меньшей мере зависит от частоты циклов деформирования (в диапазоне низких частот) и в большей – от амплитуды деформации. Следуя предложению Я.Г. Пановко [9], примем, что при гармоническом цикле деформирования форма гистерезисной петли является эллиптической, т.е.
(2)
${{f}_{i}}(\delta ,\dot {\delta }) = B\delta _{0}^{\mu }\sqrt {1 - \frac{{{{\delta }^{2}}}}{{\delta _{0}^{2}}}} \operatorname{sign} \dot {\delta },$Испытания проводились с малоразмерными моделями, геометрически подобными реальным амортизаторам. Модели имели габаритные размеры: высоту – 30 мм, ширину по подошве – 70 мм, глубину – 42 мм, высоту тоннелей – 18 мм, толщину стоек – 5 мм. Они были изготовлены из полиуретана двух марок: СУРЭЛ ТФ-228 твердостью 80 ед. по Шору по шкале А и СКУ-ПФЛ-100 твердостью 92…95 ед. по той же шкале. Для краткости первые амортизаторы назовем “мягкими”, вторые – “жесткими”.
На рис. 3 приведены статические силовые характеристики “мягкого” и “жесткого” амортизаторов, полученные на испытательной машине Galdabini Quasar 50 после нескольких тренировочных циклов медленного нагружения и разгрузки. Поиск коэффициентов жесткости для упругой характеристики (1) осуществлялся методом наименьших квадратов при помощи алгоритма метода доверительной области [10], реализованном в пакете MATLAB. Полученные коэффициенты представлены в табл. 1. При подборе коэффициентов ${{c}_{1}}$, ${{c}_{2}}$, ${{c}_{3}}$ область резкого ужесточения экспериментальной нагрузочной характеристики исключалась из рассмотрения, поскольку в проведенных динамических испытаниях [6] с невысокими перегрузками не наблюдался сколь-нибудь значительный самоконтакт стоек амортизаторов.
Таблица 1.
| Марка материала амортизатора | ${{c}_{1}}$, Н/мм | ${{c}_{2}}$, Н/мм2 | ${{c}_{3}}$, Н/мм3 |
|---|---|---|---|
| СУРЭЛ ТФ-228 | 215 | 34.7 | 2.16 |
| СКУ-ПФЛ-100 | 1140 | 195 | 11.6 |
На рис. 3 представлено сравнение экспериментальных кривых и их аппроксимаций.
Подбор коэффициентов силы неупругого сопротивления (2) выполнен, опираясь на результаты экспериментов по виброизоляции груза [6]. Эксперименты проводились с грузом массой m = 40 кг, установленным поочередно на “мягких” и “жестких” амортизаторах. Краткая сводка данных, полученных при резонансной частоте и амплитуде ускорений стола ${{a}_{{i{\kern 1pt} n}}} = 0.5g$, приведена в табл. 2.
Таблица 2.
| Марка материала амортизатора | Резонансная частота ${{\nu }_{0}}$, Гц | Эффективная жесткость ceff = m(2πυ0)2, Н/мм | Наибольшее значение коэффициента динамичности ${{\beta }_{{\max }}} = \max ({{a}_{{{\text{out}}}}}{\text{/}}{{a}_{{{\text{in}}}}})$ | Коэффициент поглощения $\psi $ |
|---|---|---|---|---|
| СУРЭЛ ТФ-228 | 11.1 | 195 | 6.2 | 0.63 |
| СКУ-ПФЛ-100 | 32.2 | 1637 | 7.1 | 0.64 |
Для модели внутреннего трения (2) энергия, рассеиваемая за период гармонических колебаний, составляет
Коэффициент поглощения при колебаниях на резонансной частоте ${{\nu }_{0}}$ с амплитудой ${{\delta }_{{\max }}}$ может быть оценен как
(3)
$\psi = \frac{{2W}}{{{{c}_{{{\kern 1pt} {\text{eff}}}}}\delta _{{\max }}^{2}}} = 2\pi \frac{{B\delta _{{\max }}^{{\mu - 1}}}}{{{{с}_{{{\text{eff}}}}}}}.$В экспериментах с помощью акселерометров измерялись ускорения стола вибростенда (${{a}_{{{\text{i}}{\kern 1pt} {\text{n}}}}}$) и груза (${{a}_{{{\text{out}}}}}$). Приведенное в табл. 2 значение коэффициента динамичности ${{\beta }_{{\max }}}$ является отношением амплитуд ускорений груза и стола в резонансном режиме. Таким же будет отношение амплитуд перемещений. Амплитуда осадки амортизатора в резонансном режиме почти не отличается от амплитуды колебаний груза, поэтому ее можно определить приближенно ${{\delta }_{{\max }}} = {{\beta }_{{\max }}}{{a}_{{{\text{i}}{\kern 1pt} {\text{n}}}}}{\text{/}}{{(2\pi {{\nu }_{0}})}^{2}}$.
При установленных осадках амортизаторов можно выполнить настройку параметров неупругого сопротивления, сохраняя эквивалентность физической и математической моделей в отношении поглощающих свойств. Поскольку характеристики физической модели [6] были определены только при одном (резонансном) режиме, то в условиях ограниченности экспериментальных данных подбор параметров $B$, $\mu $ приходится осуществлять, делая некоторые допущения. Примем $\mu = 3$ и по известному коэффициенту поглощения (3) получим для “жесткого” амортизатора $B = 230\,Н{\text{/м}}{{{\text{м}}}^{3}}$, для “мягкого” $B = 0.5\,Н{\text{/м}}{{{\text{м}}}^{3}}$. Дальнейшие расчеты выполнены при этих значениях параметров $B$ и $\mu $.
Динамика груза при поперечной (горизонтальной) амортизации. Силовая характеристика поперечной системы амортизации симметрична. Уравнение движения груза можно записать в виде
Решение этого нелинейного уравнения при гармоническом возбуждении $z = {{z}_{0}}{\text{cos}}(\omega t + \varphi )$ определяем методом гармонической линеаризации [7]. Полагая, $\delta = {{\delta }_{0}}\,\cos \omega \,t$, представим функцию эквивалентной восстанавливающей силы в виде
где коэффициенты линеаризации ${{b}_{{eq}}}$, ${{c}_{{eq}}}$ установлены по формулам(4)
${{b}_{{eq}}} = - \frac{1}{{\pi \omega {{\delta }_{0}}}}\int\limits_0^{2\pi } {{{f}_{i}}({{\delta }_{0}}\cos \xi , - \omega {\kern 1pt} {{\delta }_{0}}\sin \xi )} \sin \xi d\xi = \frac{{B\delta _{0}^{{\mu - 1}}}}{\omega },$(5)
${{c}_{{eq}}} = \frac{1}{{\pi {{\delta }_{0}}}}\int\limits_0^{2\pi } {{{f}_{e}}({{\delta }_{0}}\cos \xi )\cos \xi d\xi } = {{c}_{1}} - \frac{8}{{3\pi }}{{c}_{2}}{{\delta }_{0}} + \frac{3}{4}{{c}_{3}}\delta _{0}^{2},$(6)
${{\delta }_{0}} = \frac{{{{a}_{{in}}}}}{{\sqrt {{{{(\omega _{0}^{2} - {{\omega }^{2}})}}^{2}} + {{{(B\delta _{0}^{{\mu - 1}}{\text{/}}m)}}^{2}}} }}.$Критерием эффективности виброзащиты груза при кинематическом возбуждении служит коэффициент виброизоляции [11], характеризующий степень уменьшения ускорения, передаваемого от контейнера к грузу
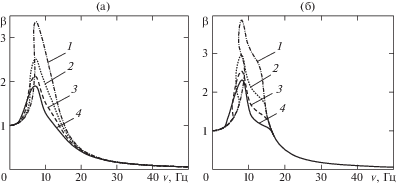
На рис. 4а приведены графики зависимости коэффициента виброизоляции груза, размещенного на “мягких” амортизаторах, от частоты возбуждения при различных значениях амплитуды ускорения контейнера.
Рис. 4.
Зависимость коэффициента виброизоляции груза от частоты при различных амплитудах ускорений контейнера: 1 – 0.5g; 2 – 0.75g; 3 – 1.0g; 4 – 1.25g: (а) – поперечная (горизонтальная) амортизация; (б) – продольная (вертикальная) амортизация.
Динамика груза при продольной (вертикальной) амортизации. Система находится в поле силы тяжести. Нижний амортизатор поджат весом груза. Верхний амортизатор приведен в соприкосновение с грузом, но не деформирован и дополнительной реакции не создает. Особенность этой нелинейной колебательной системы состоит в том, что при “мягких” амортизаторах начальное поджатие может заметно изменить ее жесткость. На рис. 5 показано смещение нагрузочных характеристик амортизаторов (штриховые кривые) при наличии начального поджатия ${{\delta }_{{st}}}$ нижнего амортизатора. Теперь нагрузочная характеристика системы в целом становится несимметричной при отсчете осадки $\delta $ от положения статического равновесия.
Рис. 5.
Смещение нагрузочных характеристик нижнего (1) и верхнего (2) амортизаторов (штриховые кривые) и характеристика восстанавливающей силы без учета веса груза (3) и с его учетом (4).
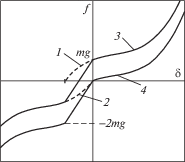
Участок характеристики $\delta > 0$ соответствует сжатию нижнего амортизатора, участок $ - {\kern 1pt} {\kern 1pt} {{\delta }_{{st}}} < \delta < 0$ – совместной работе двух амортизаторов. На участке $\delta < - \,{{\delta }_{{st}}}$ происходит отрыв груза от нижнего амортизатора. На участке совместной работы амортизаторов их симметричные нагрузочные кривые складываются и практически “линеаризуются”, образуя участок почти постоянной жесткости ${{c}^{*}} = 2mg{\text{/}}{{\delta }_{{st}}}$.
Уравнение вертикальных колебаний амортизированного груза может быть записано в виде
(7)
$m(\ddot {\delta } + \ddot {z}) = mg - H({{\delta }_{{st}}} + \delta ){{f}_{1}}({{\delta }_{{st}}} + \delta ) + H( - \delta ){{f}_{2}}( - \delta ) - {{f}_{i}},$Принимая допущение об отсутствии влияния статической нагрузки на величину рассеиваемой при колебаниях энергии и предполагая близость процесса к гармоническому, будем использовать линеаризованное выражение силы внутреннего трения с коэффициентом вязкости (4). Тогда уравнение (7) примет вид
Рассматривая гармоническое возбуждение системы $z = {{z}_{0}}\cos (\omega t + \varphi )$, найдем установившиеся колебания $\delta = \Delta + {{\delta }_{0}}{\text{cos}}\omega t$ методом прямой линеаризации функции восстанавливающей силы $f\left( \delta \right)$ [12]. Сначала определим смещение центра размаха колебаний $\Delta $ из условия равенства значений потенциальной энергии системы при амплитудных отклонениях
Нелинейное уравнение (8) решается относительно $\Delta $ при заранее задаваемых значениях амплитуды осадки амортизатора ${{\delta }_{0}}$.
Далее по методу линеаризации с весовой функцией [12] найдем резонансную частоту системы
(9)
$\omega _{0}^{2}({{\delta }_{0}}) = \frac{5}{{2m\delta _{0}^{5}}}\int\limits_{ - {{\delta }_{0}}}^{{{\delta }_{0}}} {f(\delta - \Delta ){{\delta }^{3}}d\delta } ,$При известной скелетной кривой по уравнению амплитудно-частотной характеристики (АЧХ)
Перейдем к результатам. Для груза массой $m = 40$ кг статическая осадка “мягкого” амортизатора согласно экспериментальной нагрузочной характеристике (рис. 3) составляет ${{\delta }_{{st}}} \approx 3.0\,мм$. Такая осадка заметно меняет жесткость системы. На рис. 4б представлены графики зависимости коэффициентов виброизоляции от частоты, полученные при амплитудах ускорений контейнера 0.5g; 0.75g; 1.0g; 1.25g. Отметим, что расчеты выполнены при коэффициентах перегрузки ${{a}_{{{\text{in}}}}}{\text{/}}g \leqslant 1.25$, реализуемых на вибростенде Data Physics Signal Force V400 при массе груза 40 кг, с целью дальнейшей экспериментальной проверки.
Экспериментальное исследование виброизоляции груза. Для физического моделирования виброизоляции груза в контейнере используется экспериментальная установка [6], схематично изображенная на рис. 2. Рассмотрим результаты исследования системы с “мягкими” амортизаторами. Для получения АЧХ системы на стол вибростенда подавалось кинематическое возбуждение с различными амплитудами ускорения и медленно возрастающей частотой. Скорость повышения частоты составляла 0.1 Гц/с; диапазон частот от 5 до 50 Гц. Соответствующие частотные зависимости показаны на рис. 6.
Рис. 6.
Экспериментальная зависимость коэффициента виброизоляции груза от частоты. Цифры у кривых соответствуют различным амплитудам ускорений стола вибростенда: 1 – 0.5g; 2 – 0.75g; 3 – 1.0g; 4 – 1.25g.
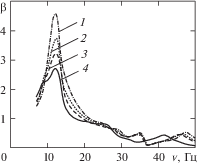
Из графиков видно, что с повышением амплитуды ускорений вибростенда наблюдается снижение пиковых значений коэффициента виброизоляции (динамичности), что косвенно свидетельствует о применимости теории эквивалентного внутреннего трения при моделировании работы полиуретановых амортизаторов. Пиковые значения ${\beta }$ в расчете (рис. 4б) и эксперименте (рис. 6) согласуются удовлетворительно. Наблюдаемый сдвиг значений резонансной частоты по расчету и в эксперименте объясняется тем, что жесткость в экспериментальной установке повышена за счет системы стабилизации (позиция 8 на рис. 2), которая представляет собой набор стержней, препятствующих боковым смещениям груза при вибрации.
Частотные зависимости, полученные экспериментально в настоящей (рис. 6) и предыдущей [6] работах авторов, несколько различаются значениями резонансных частот и максимумов коэффициентов виброизоляции, т.к. испытания проведены с амортизаторами разных партий.
Выводы. Предложена математическая модель системы виброизоляции, учитывающая нелинейный характер восстанавливающих сил полиуретановых амортизаторов тоннельного типа. Характеристики амортизаторов установлены по результатам статических и динамических испытаний. Проведена верификация модели на основе динамических испытаний с различными амплитудами ускорений стола вибростенда. Результаты, полученные для малоразмерных образцов амортизаторов, могут быть распространены на натурный объект методом подобия. Разработанная модель может быть использована в практических расчетах систем амортизации объектов.
Конфликт интересов. Авторы заявляют об отсутствии конфликта интересов.
Список литературы
Wu J.H., Li C.H., Chiu H.T., Shong Z.J., Tsai P.A. Anti-vibration and vibration isolator performance of poly(styrene-butadiene-styrene)/ester-type polyurethane thermoplastic elastomers // Polymers for Advanced Technologies. 2010. 21. P. 164.
Bek M., Betjes J., von Bernstorff B.S., Emri I. Viscoelasticity of new generation thermoplastic polyurethane vibration isolators // Preprint in Physics of Fluids. December 2017. № 29 (12) P. 42.
Mendelsohn M.A., Rudd G.E., Rosenblatt G.B. Chemical and Engineering Properties of Polyurethane Isolator Pads // Industrial & Engineering Chemistry Product Research and Development. 1975. V. 14. № 3. P. 181.
Lv Z.Q., Shu L.H. Shock Mechanics Model and Characteristic Analysis of Polyurethane Isolator with Displacement Restrictor // Advanced Materials Research. 2012. V. 503–504. P. 972.
Алашеев В.И., Белкин А.Е., Бобров А.В., Ярошевич Н.В. Анализ работы полиуретанового амортизатора тоннельного типа в условиях ударного нагружения // Известия высших учебных заведений. Машиностроение. 2017. № 5. С. 4.
Белкин А.Е., Даштиев И.З., Никитин Е.А., Сергиенко В.В. Физическое и математическое моделирование виброизоляции груза в контейнере с применением полиуретановых амортизаторов // Известия высших учебных заведений. Машиностроение. 2018. № 7. С. 11.
Коловский М.З. Нелинейная теория виброзащитных систем. М.: Наука, 1966. С. 320.
Лукомская А.И., Евстратов В.Ф. Основы прогнозирования механического поведения каучуков и резин. М.: Химия, 1975. С. 360.
Пановко Я.Г. Внутреннее трение при колебаниях упругих систем. М.: Физматгиз. 1960. С. 194.
Измаилов И.Ф., Солодов М.В. Численные методы оптимизации. М.: Физматлит, 2005. С. 304.
Бидерман В.Л. Теория механических колебаний. М.: URSS, 2017. С. 406.
Пановко Я.Г. Основы прикладной теории колебаний и удара. М.: URSS, 2015. С. 272.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин



