Проблемы машиностроения и надежности машин, 2019, № 7, стр. 72-79
МОДЕЛИРОВАНИЕ КОНТАКТНОГО ВЗАИМОДЕЙСТВИЯ ТЕЛ В ТЕПЛОВЫДЕЛЯЮЩЕМ ЭЛЕМЕНТЕ
М. П. Галанин 1, 2, *, В. В. Лукин 1, 2, А. С. Родин 1, 2
1 Институт прикладной математики им. М.В. Келдыша РАН
г. Москва, Россия
2 Московский государственный технический университет им. Н.Э. Баумана
г. Москва, Россия
* E-mail: galan@keldysh.ru
Поступила в редакцию 11.07.2019
Принята к публикации 26.08.2019
Аннотация
Применен вариант метода декомпозиции области для численного решения поликонтактной задачи термомеханического взаимодействия системы тел. Суть варианта состоит в чередовании кинематических и силовых условий, задаваемых на контактах. Проведено численное моделирование напряженно-деформированного состояния участка тепловыделяющего элемента с учетом контакта таблеток топлива друг с другом и оболочкой. Задача решена в осесимметричной термоупругой постановке. Представлены результаты расчетов, в которых количество таблеток варьировалось от 4 до 300.
1. Введение и постановка задачи. Рассмотрим задачу, позволяющую моделировать ряд термомеханических эффектов, происходящих в тепловыделяющем элементе (твэл). Он представляет собой трубу (оболочку), имеющую размеры: длина – 3–4 м, диаметр – 0.01 м, толщина – 0.001 м. В трубу помещен столб из топливных таблеток (их количество достигает нескольких сотен). В ходе работы твэла происходит нагрев таблеток до температуры около 1800 К. Контактное взаимодействие таблеток друг с другом и оболочкой оказывает существенное влияние на НДС твэла.
В статье выполнено моделирование выхода участка твэла на номинальную мощность в осесимметричном приближении. Таблетки и оболочки считаются термоупругими, поэтому эффекты, связанные с пластичностью, ползучестью и разрушением, не учтены.
2. Математическая модель. Рассмотрим в трехмерном пространстве группу n тел, занимающих область $G = \bigcup\nolimits_{\alpha = 1}^n {{{G}_{\alpha }}} $ с границей $\partial {\kern 1pt} G = \cup \partial {{G}_{\alpha }}$. Предположим, что эффектом связанности (зависимостью температуры от деформации) можно пренебречь.
Начально-краевая задача для определения распределения температуры задается обычными соотношениями [1]. Квазистационарная задача равновесия тела номера $\alpha = 1, \ldots ,n$ включает соотношения
(1)
${{u}_{i}}({\mathbf{x}},t) = u_{i}^{1}({\mathbf{x}},t),\quad {\mathbf{x}} \in S_{1}^{\alpha } \subset \partial {\kern 1pt} {\kern 1pt} {{G}_{\alpha }},$Здесь ${{u}_{i}}({\mathbf{x}},t)$ – компоненты вектора перемещения, $u_{i}^{1}({\mathbf{x}},t)$ – компоненты вектора перемещения точки, расположенной на участке $S_{1}^{\alpha }$, для которой заданы кинематические условия, ${{p}_{i}}({\mathbf{x}},t)$ – компоненты вектора внешней нагрузки, действующей на поверхности $S_{2}^{a}$, для которой заданы силовые условия.
Кроме граничных условий (ГУ) (1) на границе контакта ${{S}_{k}}$ любых двух тел $A$ и $B$ должны быть выполнены условия сопряжения по перемещениям (кинематическое условие) и напряжениям (силовое условие) [2, 3]
(3)
$\sigma _{n}^{A}({\mathbf{x}},t) = \sigma _{n}^{B}({\mathbf{x}},t),\quad {\mathbf{x}} \in {{S}_{k}}.$Считаем, что начальный зазор между контактирующими поверхностями тел равен нулю. Поверхность каждого тела с номером $\alpha $ состоит из трех участков: $S_{{1}}^{\alpha } \cup S_{{2}}^{\alpha } \cup S_{k}^{\alpha } = \partial {{G}_{\alpha }}$. В процессе нагрева положение контактных поверхностей значительно меняется и априори неизвестно.
3. Численная модель. Для численного решения задачи в статье использован метод конечных элементов (МКЭ) [2, 3].
Для учета контактного взаимодействия чаще всего применяют метод штрафных функций, метод множителей Лагранжа или их комбинации [2], но в статье использован метод декомпозиции области (МДО), главным преимуществом которого является сведение решения общей задачи контактного взаимодействия нескольких тел к последовательности решений стандартных задач механики для каждого тела по отдельности в рамках итерационного процесса. При моделировании десятков или сотен таблеток в топливном столбе это потенциально позволяет существенно упростить процедуру численного решения и уменьшить ее время. В [4] рассмотрены варианты МДО, которые отличаются порядком постановки кинематических (условие Дирихле) и силовых (условие Неймана) условий на контактной поверхности на различных итерациях. В частности, это алгоритмы Нейман–Дирихле, Нейман–Нейман и Дирихле–Дирихле.
В [5] предложен оригинальный вариант МДО, который использован для моделирования твэла. Рассмотрим его применение на примере контакта двух тел (тела A и B). На первом шаге (нулевой итерации) зададим нормальные к поверхности компоненты перемещений контактных узлов ${{\{ {{U}_{k}}\} }_{A}}$ и ${{\{ {{U}_{k}}\} }_{B}}$. Приближение выбирают из диапазона ожидаемых значений для зоны контактного взаимодействия так, чтобы контактные поверхности тел совпали. После нулевой итерации в узлах на контактных поверхностях перемещения совпадают (выполнено (2)), но не совпадают давления (условие (3)).
В дальнейшем на нечетных итерациях (с номером ${\text{2}}n + {\text{1}}$) выполняют коррекцию компонент векторов $\{ {{P}_{k}}\} _{A}^{{}}$ и $\{ {{P}_{k}}\} _{B}^{{}}$ тел $A$ и $B$(для выполнения условия (3) относительно контактных сил). Для тела $A$, например, корректирующие выражения имеют вид [5]
В работе для аппроксимации контактных давлений использованы линейные базисные функции (заданные на поверхностных элементах), а контактная сила ${{\{ {{P}_{k}}\} }_{{A,m}}}$ в узле $m$ вычислялась путем интегрирования по ячейке Дирихле, соответствующей данному узлу. Более подробно варианты вычисления контактных давлений и сил рассмотрены в [6].
На четных итерациях (с номером ${\text{2}}n$) выполняется коррекция компонент перемещений контактных узлов ${{\{ {{U}_{k}}\} }_{A}}$ и ${{\{ {{U}_{k}}\} }_{B}}$ тел $A$ и $B$ (2). Для тела $A$ корректирующие выражения имеют вид [5]
Чередование кинематических и силовых условий, задаваемых на поверхности контакта тел, выполняется до сходимости, когда оба условия (2), (3) выполнены с заданной точностью. Свойства МДО во многом определяются скоростью сходимости итераций, зависящей от параметров $\alpha _{{A,m}}^{{2n - 1}}$, $\alpha _{{A,m}}^{{2n}}$. В [5, 7] предложены разные формулы для их вычисления, в проведенных расчетах использованы соотношения
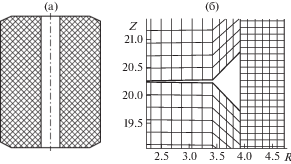
4. Результаты расчетов. В расчетах рассмотрены топливные таблетки, имеющие внутреннее отверстие и фаски по краям (рис. 1а). Использованы допущения: 1) в начальный момент времени внешний радиус таблеток совпадает с внутренним радиусом оболочки (начальный зазор равен нулю); 2) мощность тепловыделения в таблетках линейно меняется по времени от нуля до предельного значения $\phi _{L}^{{{\text{max}}}}$ = 45 кВт/м (объемная мощность тепловыделения $\phi = \phi _{L}^{{}}S$, где $S$ – площадь поперечного сечения); 3) температура оболочки остается постоянной ${{T}_{{cl}}}$ = 623 К; 4) температура таблеток в начальный момент времени равна 300 К. Для нахождения распределения температуры в таблетках на каждый момент времени решена задача теплопроводности с заданными источниками тепла, между боковыми поверхностями таблеток и внутренней поверхностью оболочки поставлено граничное условие (ГУ) третьего рода с коэффициентом теплоотдачи ${{\beta }_{w}}$ = 25 кВт/м2/К, на других поверхностях таблеток задано условие второго рода с нулевым потоком. Полученное температурное поле использовано при решении уравнения равновесия (1) (отдельно для каждого тела). Выбраны граничные условия: нижние торцы первой таблетки и оболочки закреплены в направлении оси Oz; на верхнем торце верхней таблетки задано постоянное давление ${{p}_{z}}$ = 10 МПа. На поверхности контактирующих тел поставлено условие скольжения без трения. Для выхода на заданную мощность тепловыделения сделано 10 шагов по времени, на каждом шаге – 20 итераций (для любого просчитанного количества таблеток). Теплофизические характеристики материала таблетки соответствуют диоксиду урана, а оболочки – сплаву циркония. Использованы конечные элементы (КЭ) первого порядка на четырехугольной сетке.
Рис. 1.
(а) – сечение топливной таблетки; (б) – расчетная сетка на участке области вблизи контакта двух таблеток.
Характерной особенностью задачи является существенное смещение узлов, расположенных на боковых поверхностях таблеток, относительно начального положения. Даже для нескольких таблеток в топливном столбе максимальная величина смещения достигала размера нескольких ячеек сетки в оболочке. Поэтому расчет контакта таблеток с оболочкой всегда происходил на несогласованных сетках, а применение стандартного алгоритма [5] приводило к значительному росту количества итераций при увеличении количества таблеток. Для исправления ситуации использован алгоритм аналогично методу [8]. Для топливного столба последовательно решались задачи для каждой таблетки, начиная с первой. При этом для первых пяти итераций на нижнем торце таблетки всегда ставилось кинематическое условие (перемещения брались равными перемещениям точек на верхнем торце предыдущей, уже посчитанной, таблетки), а на верхнем торце – силовое условие. После пяти итераций граничных условий на обоих торцах чередовались стандартным образом. В процессе счета нулевой или четной итерации на боковых поверхностях таблеток и на внутренней поверхности оболочки ставились силовые условия, а для нечетной итерации – кинематические условия. В целях улучшения сходимости на внешней поверхности оболочки на четных итерациях ставилось кинематическое условие (значение перемещения бралось с предыдущей итерации): для контактной пары таблетка/таблетка ${{\gamma }_{A}}$ = 0.5 (тело $A$ соответствует нижней таблетке); для контактной пары оболочка/таблетка ${{\gamma }_{A}}$ = 10 (тело $A$ соответствует оболочке). Предложенный алгоритм позволил получить максимальные относительные расхождения по перемещениям (сравнивались перемещения на двух соседних итерациях) и интегральным контактным силам (сравнивались распределенные контактные силы, проинтегрированные по противолежащим контактным поверхностям) в пределах от 10–3 до 10–2 для любого количества таблеток.
Все рисунки соответствуют заключительному моменту времени после проведения 20 итераций (на поверхности контакта таблеток и оболочки выполнено кинематическое условие). Координаты и перемещения на графиках нормированы на 0.001 м, а напряжения – на 1 МПа.
В первой серии расчетов рассмотрен участок твэла, соответствующий четырем таблеткам, в которых задана линейная мощность тепловыделения, не меняющаяся вдоль оси Oz. В таблетках построена сетка с шагом 0.2, а в оболочке – с шагом 0.1. На рис. 1б показана расчетная сетка вблизи контакта второй и третьей таблеток (на момент окончания расчета).
Для оценки качества решения контактной задачи интерес представляют распределения нормальных перемещений и напряжений вблизи контактных поверхностей таблеток и оболочки. На рис. 2, 3 показаны графики, демонстрирующие распределения радиальных перемещений и напряжений вдоль сечения, соответствующего внутренней поверхности оболочки (на участке напротив второй и третьей таблеток).
Рис. 2.
Распределение радиальных перемещений на поверхностях таблеток (график 1) и оболочки (график 2).
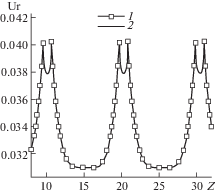
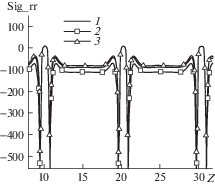
Рис. 3.
Распределение контактных давлений (график 1) и радиальных напряжений в таблетках (график 2) и оболочке (график 3).
На рис. 2 приведены распределения радиального перемещения для таблеток (график 1) и для оболочки (график 2). Графики совпадают везде, кроме участков, расположенных между фасками таблеток (рис. 1б), где контакта не происходит. Также отличия наблюдаются для узлов, расположенных в углах фасок: данные узлы оказываются напротив поверхностных элементов сетки оболочки, которые находятся в контакте не полностью, а частично, поэтому для них условия (2), (3) выполнены неточно.
На рис. 3 приведены три графика: контактное давление в узлах на боковых поверхностях таблеток (график 1, график давления в узлах на поверхности оболочки визуально совпадает с графиком 1), радиальное напряжение в центрах ячеек, примыкающих к поверхностям таблеток (график 2), радиальное напряжение в центрах ячеек, примыкающих к внутренней поверхности оболочки (график 3). Контактное давление вдоль большей части боковой поверхности каждой таблетки является почти постоянным (около 90 МПа), но вблизи углов фасок находятся концентраторы напряжений. Значения давлений в этих зонах увеличиваются при измельчении сетки, но интегральная контактная сила, действующая на поверхность, остается неизменной. На графиках хорошо видны интервалы, соответствующие участкам оболочки, расположенным вне контакта с таблетками: на этих интервалах, возникают небольшие растягивающие радиальные напряжения.
В процессе нагрева на поверхностях контакта таблеток друг с другом возникали растягивающие осевые напряжения, данный факт использовался в качестве критерия выхода соответствующего узла из контакта. В конце расчета на каждой торцевой поверхности таблетки в контакте оставались только два узла, расположенные ближе всего к внутреннему отверстию, а остальные узлы (на торце) выходили из контакта (это хорошо заметно на рис. 1б).
В [8] приведены результаты расчетов для похожей постановки задачи и выполнено их сравнение с результатами, полученными при решении контактной задачи с помощью метода множителей Лагранжа. Сравнение показало достаточно хорошее качественное и количественное сходство рассчитанных перемещений и напряжений в топливных таблетках и оболочке.
Во второй серии расчетов рассмотрен участок твэла, соответствующий 10 таблеткам (шаг сетки в таблетках – 0.2, в оболочке – 0.1). В первом расчете линейная мощность тепловыделения не менялась вдоль оси Oz, во втором расчете она увеличивалась линейным образом с ростом z, в третьем расчете она менялась вдоль оси по синусоидальному закону.
На рис. 4 приведены распределения радиального перемещения вдоль сечения, соответствующего внутренней поверхности оболочки для трех законов тепловыделения. Как и для предыдущей серии расчетов, аналогичные графики для таблеток визуально неотличимы от показанных (за исключением участков между фасками, где контакта не происходит).
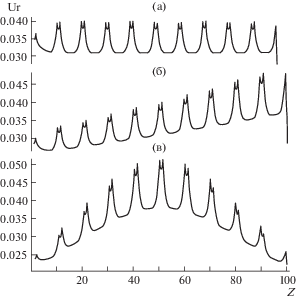
Рис. 4.
Распределения радиального перемещения (10 таблеток) для трех зависимостей мощности тепловыделения.
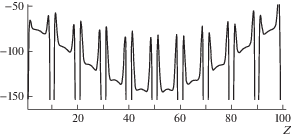
На рис. 5. показано распределение радиальных напряжений в центрах ячеек, примыкающих к внешним поверхностям таблеток, для тепловыделения по синусоидальному закону. Для лучшего визуального восприятия диапазон выводимых напряжений ограничен величиной 150 МПа, но в углах фасок, как и ранее, возникали концентраторы напряжений, в которых значения напряжений достигали величины 500–700 МПа, как и на рис. 3.
Из приведенных графиков видно, что усредненные значения перемещений и напряжений вблизи поверхности контакта таблеток с оболочкой меняются в соответствии с использованным законом тепловыделения в таблетках.
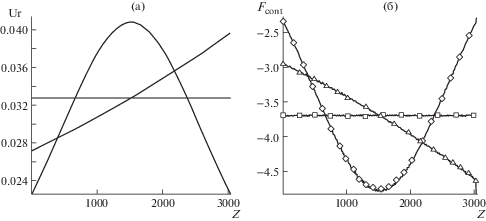
В третьей серии расчетов рассмотрен участок твэла, соответствующий 300 таблеткам (шаг сетки в таблетках – 0.3, в оболочке – 0.16). Использованы три зависимости мощности тепловыделения: постоянная, меняющаяся вдоль оси по линейному закону и меняющаяся по синусоидальному закону. Аналогичная рис. 2, 3, 4 картина распределений локальных величин перемещений и напряжений не воспринимается из-за большого количества тел, поэтому на рис. 6 показаны интегральные характеристики контакта таблеток с оболочкой.
Для боковой поверхности каждой таблетки вычислены среднее значение радиального перемещения и интегральная контактная сила. На рис. 6а приведены три графика распределений средних перемещений для трех расчетов с различными законами тепловыделения (каждый график построен по 300 точкам). На рис. 6б показаны аналогичные графики интегральных контактных сил, маркерами обозначены три графика, соответствующие значениям интегральных контактных сил на участках оболочки напротив каждой из таблеток. Для заключительного момента времени после 20 итераций (на контакте выполнено кинематическое условие) характерное относительное расхождение между интегральными силами в таблетках и на участках оболочки во всех расчетах составляло 10–2. Осевое перемещение верхней таблетки превышало 0.04 м (высота 4 таблеток), поэтому верхние таблетки смещались вдоль оболочки на сотни ячеек сетки относительно начального положения.
5. Заключение. Представлено применение варианта метода декомпозиции области для численного моделирования НДС участка твэла с учетом контакта топливных таблеток друг с другом и оболочкой. Задача решена в осесимметричной термоупругой постановке. Для численного решения использован метод конечных элементов с конечными элементами первого порядка на четырехугольной сетке. Предложен численный алгоритм чередования кинематических и силовых условий на контактных поверхностях, позволяющий уменьшить количество итераций для решаемой задачи. Расчеты показали, что описанный алгоритм решения задачи является достаточно эффективным и позволяет моделировать участки стержня с сотнями таблеток.
Благодарности. Авторы выражают глубокую благодарность Игорю Васильевичу Станкевичу за оказанную помощь и полезные советы.
Конфликт интересов. Авторы заявляют, что у них нет конфликта интересов.
Список литературы
Зарубин В.С., Кувыркин Г.Н. Математические модели механики и электродинамики сплошной среды. М.: МГТУ им. Н.Э. Баумана. 2008. С. 512.
Wriggers P. Computational Contact Mechanics. Berlin-Heidelberg: Springer-Verlag. 2006. P. 520.
Бате К.Ю. Методы конечных элементов. М.: Физматлит. 2010. С. 1024.
Toselli A., Widlund O. Domain Decomposition methods – Algorithms and Theory. Berlin-Heidelberg: Springer-Verlag. 2005. P. 450.
Цвик Л.Б. Принцип поочередности в задачах о сопряжении и контакте твердых деформируемых тел // Прикладная механика. 1980. Т. 16. № 1. С. 13.
Родин А.С. Решение задачи контакта двух упругих тел методом Шварца при использовании сеток с существенно отличающимися шагами // Препринты ИПМ им. М.В. Келдыша. 2017. № 120. С. 28.
Галанин М.П., Глизнуцина П.В., Лукин В.В., Родин А.С. Исследование влияния итерационных параметров на сходимость метода Шварца при решении задачи контакта упругих тел // Mathematica Montisnigri. 2018. V. XLI. P. 33.
Галанин М.П., Крупкин А.В., Кузнецов В.И., Лукин В.В., Новиков В.В., Родин А.С., Станкевич И.В. Математическое моделирование контактного взаимодействия системы термоупругих тел методом Шварца для многомерного случая // Известия высших учебных заведений. Машиностроение. 2016. № 12 (681). С. 9.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин