Проблемы машиностроения и надежности машин, 2019, № 7, стр. 97-104

1. Введение. Особенностью современных высокотемпературных композиционных материалов (ВКМ), например, углерод-углеродных, углерод-керамоматричных композитов, является их необратимое деформирование как при комнатной, так и при повышенной температурах. В общем случае диаграммы деформирования нелинейны, при разгрузке образуются остаточные деформации [1]. Для аналитического описания этих эффектов могут быть использованы теории термопластичности, основанные на традиционном подходе с применением понятия поверхности нагружения [2–5]. В случае изотропных материалов предполагается, что тензор полных деформаций состоит из упругой, термической и пластической составляющих. Модуль упругости, коэффициент Пуассона, коэффициент температурного расширения, а также предел текучести и другие материальные параметры зависят от температуры. История деформирования изотропного материала описывается параметром Одквиста. Алгоритмы расчета элементов конструкций должны содержать процедуру определения предельной нагрузки, при которой происходит переход твердого тела из упругого состояния в пластическое. Также экспериментально должно быть изучено поведение поверхности нагружения при термосиловом нагружении. Несмотря на определенную громоздкость, этот подход может быть распространен на случай анизотропного тела.

В настоящей статье для ВКМ предлагается вариант соотношений эндохронной теории термопластичности для анизотропного тела. В этой теории ключевую роль играет параметр внутреннего времени, феноменологически описывающий необратимый характер деформирования [6]. Определяющие соотношения, включающие этот временеподобный параметр, записываются либо в виде соотношений наследственного типа, либо в виде дифференциально нелинейных зависимостей. В отличие от традиционного подхода в явном виде не используется понятие поверхности нагружения, а также отсутствует разделение деформаций на упругую и пластическую составляющие. Опыт применения теории показывает, что она эффективна в случае материалов, имеющих на микроуровне гетерогенную структуру, например, для композитов, геоматериалов. Нелинейное деформирование таких материалов начинается при сравнительно малых нагрузках, что затрудняет экспериментальное определение величины напряжения, при котором происходит переход из упругого состояния в пластическое.

С помощью эндохронной теории пластичности можно получить удовлетворительные результаты при анализе неупругого поведения композитов на основе тканого наполнителя, многослойных волокнистых композитов [1, 7, 8]. Разработка эндохронной теории термопластичности для анизотропных материалов является естественным развитием данного направления в теории пластичности. Применяемый в статье термин “пластическое деформирование” понимается в обобщенном смысле как необратимое, независящее от фактора времени деформирование.

Определяющие соотношения. Для описания деформирования ВКМ при термосиловой нагрузке используем вариант эндохронной теории термопластичности. Обобщая результаты работ [6, 7], определяющие соотношения запишем в виде

Здесь σ_ij и ε_ij – тензоры напряжений и малых деформаций, Т – изменение температуры, E_ijkl[z(ξ)], B_ij[z(ξ)] – материальные функции, z(ξ) – внутреннее время, описывающее историю деформирования. Для него справедливо равенство dz = dξ/f(ξ), где f(ξ) – материальная функция, причем f(ξ) > 0, f(0) = 1. Выражение для меры внутреннего времени ξ представим так где r_ijkl – положительно определенный симметричный тензор IV ранга материальных параметров, m > 0 – материальный параметр, описывающий необратимое деформирование при изменении температуры. В равенстве (2) изменение температуры наряду с тензором деформаций рассматривается как параметр нагружения, отражающий историю деформирования.

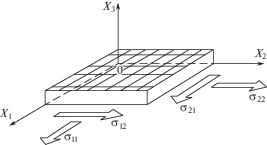
Предполагая в дальнейшем применение данной теории для описания деформирования ВКМ, рассмотрим соотношения для ортотропного тела при плоском напряженном состоянии (рис. 1). В случае применения в (1) ядер экспоненциального вида определяющие соотношения в матричном виде можно представить следующим образом

Здесь {σ} = (σ₁₁, σ₂₂, σ₁₂)^T и {ε} = (ε₁₁, ε₂₂, γ₁₂)^T – векторы напряжений и деформаций соответственно, [α_s] = diag(α_s1, α_s2, α_s3), [α_T] = diag(α_t1, α_t2, 0) – матрицы материальных параметров. Матрица жесткости материала [D] имеет обычный вид где E₁, E₂, G₁₂, ν₁₂, ν₂₁ – характеристики упругости ортотропного материала, $E_{{1,\,2}}^{{{\kern 1pt} '}} = {{E}_{{1,\,2}}}{\text{/}}(1 - {{\nu }_{{12}}}{{\nu }_{{21}}})$, {B} = [D]{β}, {β} = (β₁₁, β₂₂,0)^T – вектор коэффициентов линейного температурного расширения. Мера внутреннего времени (2) определена следующей формулой Здесь положительно определенная матрица материальных параметров [R] имеет вид

Материальные параметры определяются из условия наилучшего совпадения экспериментальных и теоретических результатов. Для этого можно использовать численные процедуры, с помощью которых производится обработка результатов базовых экспериментов [1]: одноосное нагружение вдоль осей ОХ₁ и ОХ₂; чистый сдвиг в плоскости ОХ₁Х₂; нагрев образцов материала.

Далее для удобства вычислений запишем определяющие соотношения (3) в виде

где

На основании (5) и (6) соотношения можно представить в дифференциальном виде

Здесь {σ_t} = ( σ_11t, σ_22t, 0)^T – вспомогательный вектор термических напряжений.

Для некоторых ВКМ, например, для углерод-углеродных материалов на основе тканого наполнителя, в силу малости коэффициентов ν₁₂ и ν₂₁ эффектом Пуассона можно пренебречь [1]. Тогда принимая ν₁₂= ν₂₁≈ 0, определяющие соотношения можно упростить. В этом частном случае для некоторых видов нагружения определяющие соотношения можно проинтегрировать и получить сравнительно простые аналитические выражения. В общем случае соотношения (7) целесообразно интегрировать численно.

2. Описание сложного нагружения. Рассмотрим сложное нагружение ортотропного ВКМ. Для этого предположим, что компоненты вектора напряжений и изменение температуры Т зависят от параметра нагружения р, т.е. имеют место равенства

Преобразуем соотношения (7). Исключая в первом соотношении производную $\frac{{d\{ {{\sigma }_{t}}\} }}{{d\xi }}$, получим Здесь [S] = [D]^–1 – матрица упругих податливостей ортотропного тела. Принимая во внимание (8) и равенства из уравнения (9) следует Символы со штрихами обозначают производную по переменной р.

Введем обозначения

Уравнение (10) слева умножим на выражение $\frac{{d{{{\{ \varepsilon \} }}^{{\text{T}}}}}}{{d\xi }}[R]$. После преобразований в итоге будем иметь равенство

где

Формулу (4) с учетом (8) представим таким образом

Тогда из (11) и (12) получим уравнение

Решая его относительно производной $\frac{{dp}}{{d\xi }}$, получим нелинейное обыкновенное дифференциальное уравнение 1-го порядка относительно функции p(ξ)

Знак “+” имеет место при dp > 0, т.е. при нагрузке, знак “–” – при dp < 0, т.е. при разгрузке. Для определения деформаций следует использовать равенство (10). Вектор термических напряжений находим из второго уравнения системы (7), которое представим так

Таким образом, уравнения (13), (10) и (14) образуют систему уравнений для анализа напряжений и деформаций в случае сложного нагружения образца ВКМ, задаваемого равенствами (8).

3. Частный случай: изменение температуры при постоянном растягивающем напряжении. Воспользовавшись уравнениями (10), (13), (14), выполним анализ варианта сложного нагружения. Для наглядности изучим поведение образца материала при одноосном нагружении в направлении оси ОХ₁ и нагреве. Эффект Пуассона не учитываем. Кроме этого, при нагреве не учитываем деформации в направлении оси ОХ₂, т.е. предполагаем, что β₂₂ ≈ 0. Принимаем также, что r₁₁ = 1. В расчетах используем известное выражение f(ξ) = 1 + βξ, где β > 0 – материальный параметр, позволяющее в ряде случаев получить аналитические решения [6, 7].

На первом этапе нагружения образец материала предварительно растягивается до напряжения $\sigma _{{11}}^{*}$. Тогда в равенствах (8) принимаем {f(p)} = (p, 0, 0)^T, φ(p) = 0. Отсюда следует, что

Из уравнения (14) при условии, что φ'(p) = 0 и σ_11t(0) = 0, получим σ_11t(ξ) = 0. С учетом соотношения σ₁₁= р из уравнения (13) имеем

Здесь при растяжении используем знак “+”. Тогда из уравнения (10) следует

В соответствии с (15) и (16) для случая растяжения имеем dξ = dε₁₁. Тогда решением уравнения (15) с учетом начального условия σ₁₁(0) = 0 будет зависимость

Рассмотрим второй этап нагружения. Полагаем, что в момент ξ = ξ* при постоянном напряжении $\sigma _{{11}}^{*} = {{\sigma }_{{11}}}(\xi _{{}}^{*})$ начинается нагрев материала. Тогда при ξ ≥ ξ* имеем $\{ f(p)\} = {{(\sigma _{{11}}^{*},0,0)}^{{\text{T}}}}$, φ(p) = р. Отсюда следуют равенства

После преобразований система уравнений (10), (13), (14) примет вид

Здесь введены функция $B(\xi ) = {{\alpha }_{{s1}}}\sigma _{{11}}^{*} + ({{\alpha }_{{s1}}} - {{\alpha }_{{t1}}}){{\sigma }_{{11t}}}$ и величина ρ = β₁₁/m.

Уравнения (17) интегрируются численно при ξ ≥ ξ* для начальных условий ξ = ξ*, Т = 0, σ_11t = 0, ε₁₁= ξ* = $\varepsilon _{{11}}^{*}$. При нагреве следует брать знак “+”, а в случае охлаждения используем знак “–”. С помощью уравнений (17) можно описывать деформирование образца ВКМ при нагреве, при термоциклировании и одновременном действии постоянного растягивающего напряжения.

4. Численный пример. Для рассмотрения эффектов нелинейного деформирования, прогнозируемых с помощью системы дифференциальных уравнений (17), выполним описание поведения образца гипотетического материала с материальными параметрами: E₁ = 20 ГПа, β₁₁ = 1.8 ⋅ 10^–6 1/град, α_s1 = 150, α_t1 = 30, β = 5, m = 0.24 ⋅ 10^–6 1/град. На этапе предварительного нагружения имеем 0 ≤ ξ ≤ ξ*, при последующем нагружении – ξ* ≤ ξ ≤ ξ_k. Зададим значения ξ* = 0; 0.0025; 0.005; 0.0075; 0.01, что соответствует напряжениям $\sigma _{{11}}^{*}$ = 0 МПа, 42 МПа, 70 МПа; 91 МПа; 105 МПа. При этом для всех случаев принимаем значение ξ_к= 0.02.

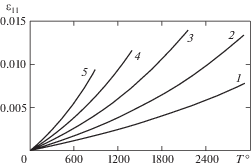
На рис. 2 приведены результаты расчета. Предварительное растяжение образца существенным образом влияет на деформацию, возникающую при нагреве. При этом касательный коэффициент температурного расширения $\frac{{d{{\varepsilon }_{{11}}}}}{{dT}}$ возрастает. Такой характер деформирования при нагреве экспериментально установлен для углерод-углеродного композита [9].

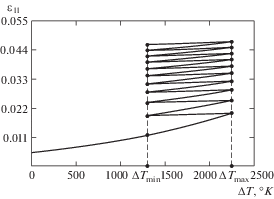
Уравнения (17) позволяют прогнозировать поведение ВКМ при циклическом изменении температуры. На рис. 3 показан характер деформирования образца материала для десяти циклов “нагрев–охлаждение” на интервале T_min ≤ T ≤ T_max, где T_min = 1300 K, T_max = 2250 K при действии постоянного растягивающего напряжения $\sigma _{{11}}^{*}$.

На рис. 4 показан график изменения максимального и минимального значений деформации ε₁₁ в зависимости от количества циклов термонагружения N (точками отмечены и для наглядности соединены отрезками те же значения деформаций, что и на рис. 3).

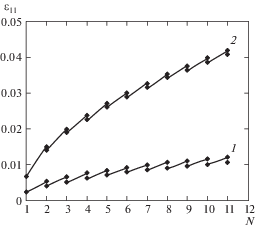
Для сравнения на рис. 4 показаны максимальные и минимальные значения деформации ε₁₁ при $\sigma _{{11}}^{*}$ = 0. Напряжение $\sigma _{{11}}^{*}$ существенным образом влияет на характер деформирования. Представленный на рис. 4 график при $\sigma _{{11}}^{*}$ = const качественно совпадает с экспериментально установленным для ВКМ на основе углеродных волокон и карбидокремниевой матрицы [10].

5. Заключение. В настоящей статье предложен вариант эндохронной теории термопластичности ВКМ, в котором мера внутреннего времени определена в пространстве малых деформаций и температуры. Такая формулировка позволяет учитывать историю их изменения. Для ортотропных высокотемпературных композиционных материалов при плоском напряженном состоянии при использовании ядер экспоненциального вида записаны дифференциально нелинейные соотношения, удобные при численном анализе. Они позволяют описывать эффекты нелинейного деформирования при сложном термосиловом нагружении, т.е. при непропорциональном изменении компонент тензора напряжений и температуры. Теория предсказывает такие эффекты, как нелинейное деформирование и увеличение касательного коэффициента термического расширения при нагреве, влияние на него предварительного силового нагружения, деформирование материала при термоциклировании в условиях действия силовой нагрузки. Некоторые из этих эффектов подтверждены при экспериментальном исследовании деформирования образцов высокотемпературных композиционных материалов различного вида. Дальнейшее накопление экспериментальных данных о деформировании анизотропных ВКМ и их анализ, с одной стороны, позволит внести при необходимости коррективы в теорию, а с другой стороны, будут способствовать разработке адекватных математических моделей элементов конструкций из высокотемпературных композиционных материалов при интенсивном термосиловом нагружении.