Проблемы машиностроения и надежности машин, 2019, № 7, стр. 20-29
Математическое моделирование и коррекция параметров ракеты пакетной схемы с использованием гибридных алгоритмов оптимизации
П. М. Шкапов 1, *, В. Д. Сулимов 1, А. В. Сулимов 2
1 Московский государственный технический университет им. Н.Э. Баумана
г. Москва, Россия
2 Филиал Московского государственного университета им. М.В. Ломоносова
г. Севастополь, Россия
* E-mail: spm@bmstu.ru
Поступила в редакцию 22.07.2019
Принята к публикации 26.08.2019
Аннотация
Рассматривается обратная задача коррекции параметров математической модели жидкостной ракеты по модальным данным. Подвижность жидкости в топливных баках при изгибных колебаниях корпуса моделируется системой осцилляторов. Решение обратной задачи получено с использованием оптимизационного подхода. Представлены два новых гибридных алгоритма глобальной оптимизации. Приведен численный пример коррекции характеристик межблочных связей ракеты пакетной схемы компоновки.
1. Современные подходы к исследованию сложных аэрокосмических систем основаны на применении методов математического моделирования [1, 2]. К этому направлению относятся работы сотрудников одной из ведущих отечественных научных школ, которую возглавлял академик РАН К.С. Колесников (1919–2016 гг.) [3]. Оптимальное проектирование, включая междисциплинарную проблематику, предъявляет высокие требования к характеристикам моделей. Прямое моделирование реальных объектов не обеспечивает требуемое качество соответствующих аналитических моделей. Актуальным направлением исследований является разработка эффективных численных методов коррекции математических моделей аэрокосмических систем с использованием модальных данных, полученных при измерениях [4, 5]. Процедуры коррекции существенно связаны с формулировкой и последующим решением обратной задачи на собственные значения [6]. Разработаны достаточно эффективные методики коррекции параметров моделей исследуемых систем. При реализации численных процедур коррекции необходимо учитывать корректность постановки обратной задачи, неполноту и зашумленность измеряемой информации, возможное наличие в спектрах систем кратных частот и др. Во многих приложениях возникают обратные задачи, которые относятся к классу некорректно поставленных, что предполагает применение специальных методов регуляризации [7, 8]. Критериальные функции обратных задач в общем случае являются многомерными, непрерывными, многоэкстремальными и не всюду дифференцируемыми. Поэтому для решения задач коррекции моделей систем и содержательно близких к ним задач вычислительной диагностики (обнаружения повреждений) систем применяют методы глобальной оптимизации [9]. При определении каждого текущего значения критериальной функции в точках допустимой области необходимы значительные вычислительные ресурсы. Этим обусловлена актуальность направления, связанного с созданием эффективных алгоритмов коррекции моделей систем по измеряемым модальным данным. Рассматриваемый подход основан на разработке и применении математических моделей систем, численных методов определения основных динамических характеристик систем, методов теории обратных задач, методов глобальной недифференцируемой оптимизации.
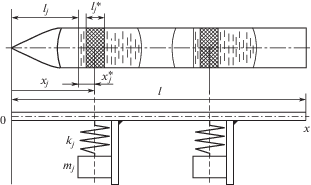
2. Рассмотрим упругие колебания жидкостной ракеты (блока) с топливными баками, частично заполненными жидкостью. Актуальным приближением аналитической модели блока является прямой неоднородный стержень с упруго подвешенными массами [10] (рис. 1).
Продольная ось $Ox$ блока направлена от его вершины к хвостовой части; две другие оси образуют вместе с продольной правую прямоугольную декартову систему координат $Oxyz$. Полная длина блока $l = 25$ м; радиус каждого топливного бака равен $r = 0.75$ м. Исходными данными для вычислений служат функции распределения массы $m(x)$ и изгибной жесткости $EI(x)$ по длине стержня; координата $x$ отсчитывается от левого конца стержня вдоль его осевой линии. Стержень разбит на семь участков. Используются масштабы массы и изгибной жесткости стержня: $m(x) = \bar {m} \cdot {{m}_{0}}$, $EI(x) = \overline {EI} \cdot E{{I}_{0}}$, где ${{m}_{0}} = 147.15$ кг и $E{{I}_{0}} = 103.005 \cdot {{10}^{6}}$ Н м2 [10]. Каждая упруго подвешенная масса (осциллятор) является механическим аналогом одного (низшего) тона колебаний жидкости в топливном баке: ${{l}_{j}}$ – расстояние от вершины блока до невозмущенной свободной поверхности жидкости в $j$-м баке; $l_{j}^{*}$ – параметр длины, используемый для определения объема (массы) колеблющейся жидкости; ${{x}_{j}}$ – координата точки подвеса осциллятора; $x_{j}^{*}$ – расстояние от невозмущенной свободной поверхности жидкости до точки подвеса осциллятора; ${{k}_{j}}$ – коэффициент жесткости $j$-го осциллятора; ${{m}_{j}}$ – масса осциллятора; $j = 1,{\text{ }}2$. Значения параметров участков неоднородного стержня, включая длины ${{l}_{i}}$ участков ($i$ – номер участка), приведены в табл. 1 [10].
Таблица 1
| $i$ | ${{\bar {m}}_{i}}$ | $\overline {E{{I}_{i}}} $ | $\frac{{{{m}_{0}}{{{\bar {m}}}_{i}}}}{{E{{I}_{0}}\overline {E{{I}_{i}}} }}$ | ${{l}_{i}},{\text{м}}$ | ${{m}_{0}}\bar {m}_{j}^{*}$, кг |
|---|---|---|---|---|---|
| 1 | 2.5 | 2.0 | 0.179 ⋅ 10–5 | 2.5 | |
| 2 | 3.5 | 4.0 | 0.125 ⋅ 10–5 | 2.5 | |
| 3 | 2.0 | 3.0 | 0.0954 ⋅ 10–5 | 1.25 | |
| 4 | 8.0 | 2.0 | 0.572 ⋅ 10–5 | 0.81 | |
| 4* | 667.08 | ||||
| 5 | 8.0 | 2.0 | 0.572 ⋅ 10–5 | 5.44 | |
| 6 | 2.0 | 5.0 | 0.0572 ⋅ 10–5 | 2.5 | |
| 7 | 6.0 | 3.0 | 0.286 ⋅ 10–5 | 0.81 | |
| 7* | 470.88 | ||||
| 8 | 6.0 | 3.0 | 0.286 ⋅ 10–5 | 4.19 | |
| 9 | 3.0 | 5.0 | 0.0858 ⋅ 10–5 | 5.0 |
В верхнем баке ($i = 4$) находится окислитель плотности 11180 кг/м3; в нижнем баке ($i = 6$) – горючее плотности 7848 кг/м3. Сосредоточенные массы ${{m}_{0}}\bar {m}_{j}^{*} = {{m}_{j}}$ осцилляторов расположены в узле 4* между участками 4 и 5 (667.08 кг), а также в узле 7* между участками 7 и 8 (470.88 кг).
Коэффициент жесткости каждого осциллятора ${{k}_{j}}$ выбирают так, чтобы частота собственных колебаний массы ${{m}_{j}}$ была равна частоте собственных колебаний жидкости в неподвижном баке: ${{k}_{1}}$ = 0.16544 ⋅ 10–6 Н/м; ${{k}_{2}}$ = 0.11678 ⋅ 10–6 Н/м.
С целью исследования пространственных упругих колебаний блока разработана его конечно-элементная модель. Блок представлен ансамблем одномерных конечных элементов, соединенных между собой в узлах; длина каждого элемента равна длине моделируемого участка разбиения. Инерционные и упругие характеристики конечно-элементной модели для исследования продольных и крутильных колебаний блока получены эквивалентным пересчетом данных, представленных в табл. 1, с учетом геометрических параметров блока. Подвижность жидкости в топливных баках учитывается только при изгибных колебаниях блока в плоскостях $Oxy$, $Oxz$ и моделируется системой осцилляторов.
Обобщенная задача на собственные значения для упругой пространственной системы, дискретизированной с использованием метода конечных элементов, имеет вид [9]
где $M,K$ – соответственно глобальные матрицы инерции (масс) и жесткости системы; $\lambda $ – собственное значение, $\lambda = {{\omega }^{2}}$; $\omega - $ круговая частота собственных колебаний; $\psi $ – собственный вектор, $\psi \in {{{\text{R}}}^{m}}$, ${{{\text{R}}}^{m}}{\text{ }} - {\text{ }}m$-мерное евклидово пространство; собственный вектор нормируется по условию ${{\psi }^{T}}M\psi = 1$, $T$ – символ транспонирования. При исследовании собственных колебаний упругих систем с большим числом степеней свободы достаточно учитывать ограниченное число низших спектральных составляющих, поэтому для численного решения задачи (1) целесообразно использование метода итерации подпространства [11]. Основной целью метода является определение ${{n}_{p}}$ низших собственных значений и соответствующих им собственных векторов (собственных пар), которые удовлетворяют матричному уравнению здесь $\Lambda = {\text{diag}}({{\lambda }_{i}})$, т.е. диагональная матрица размера ${{n}_{p}} \times {{n}_{p}}$, содержащая собственные значения; $\Psi = [{{\psi }^{1}},...,{{\psi }^{p}}]$. Собственные векторы должны также удовлетворять условиям ортогональности ${{\Psi }^{T}}K\Psi = \Lambda $; ${{\Psi }^{T}}M\Psi = I$; где I– единичная матрица порядка ${{n}_{p}}$. Уравнение (2) формулирует необходимые и достаточные условия того, что векторы, содержащиеся в матрице $\Psi $, являются собственными векторами.Получено численное решение обобщенной задачи на собственные значения (1) (прямой задачи) для конечно-элементной модели блока. Определены – две низшие частоты изгибных колебаний блока в плоскостях $Oxy$ и $Oxz$ с учетом подвижности жидкости, имеющие одинаковое значение 4.0335 Гц. Сравнение со значением аналогичной составляющей спектра частот блока, вычисленным методом начальных параметров и равным 4.036 Гц [10], дает оценку относительной погрешности в 0.062%.
Рассмотрим аналитическую модель ракеты пакетной схемы, составленной из двух одинаковых блоков, характеристики которых приведены выше. Введем узлы межблочных связей, моделируемые пружинными элементами, размещенными в поперечных сечениях, соответствующих стыкам четвертого и пятого, а также седьмого и восьмого участков каждого блока. Верхний и нижний узлы связей имеют номинальные жесткостные характеристики (в системе координат $Oxyz$): $C_{x}^{{\text{в}}}$ = 0; $C_{y}^{{\text{в}}} = C_{z}^{{\text{в}}}$ = 0.8 ⋅ 10–7 Н/м; $C_{x}^{{\text{н}}} = C_{y}^{{\text{н}}} = C_{z}^{{\text{н}}}$ = 0.8 ⋅ 10–7 Н/м. Предположим, что значения характеристик могут изменяться, причем их целесообразно задать в виде: $c_{y}^{{\text{в}}} = C_{y}^{{\text{в}}} \cdot {{x}_{1}}{\text{/}}100$; $c_{z}^{{\text{в}}} = C_{z}^{{\text{в}}} \cdot {{x}_{2}}{\text{/}}100$; $c_{x}^{{\text{н}}} = C_{x}^{{\text{н}}} \cdot {{x}_{3}}{\text{/}}100$; $c_{y}^{{\text{н}}} = C_{y}^{{\text{н}}} \cdot {{x}_{4}}{\text{/}}100$; $c_{z}^{{\text{н}}} = C_{z}^{{\text{н}}} \cdot {{x}_{5}}{\text{/}}100$; здесь ${{x}_{i}}$ – переменные модели, определяющие текущие значения характеристик межблочных связей: $0 \leqslant {{x}_{i}} \leqslant 100\% $, $i = \overline {1.{\text{ }}5} $.
Анализ результатов численного решения прямой задачи для конечно-элементной модели ракеты пакетной схемы при различных значениях переменных ${{x}_{i}}$, $i = \overline {1.{\text{ }}5} $ позволяет сделать заключение: определены собственные пары ${{n}_{p}}$ низших тонов собственных колебаний объекта (задано ${{n}_{p}} = 48$, что соответствует учету собственных частот колебаний до 65 Гц). По завершении вычислений решающий алгоритм автоматически упорядочивает собственные значения по возрастанию (имеет также место соответствующее упорядочение собственных пар). При изменении переменных модели отмечена перенумерация (перестановка) собственных пар. Это указывает на принципиальную возможность, при определенных сочетаниях значений переменных модели, появления в собственных спектрах объекта кратных и почти кратных собственных значений, что является характерным для подобных систем и определяет особенности критериальных функций формулируемых обратных задач.
3. Рассмотрим обратную задачу коррекции параметров объекта по модальным данным, которая в рамках выбранной математической модели описывается операторным уравнением
где $X,Y$ – гильбертовы пространства; $A$ – компактный линейный оператор, действующий из $X$ в $Y$. Правая часть возмущенного операторного уравнения представляет приближенные входные данные ${{y}^{\delta }}$, определенные по результатам измерений. Предположим, что погрешность задания входной информации $\delta $ известна и имеет место ${\text{|| }}{{y}^{\delta }} - y{\text{ ||}} \leqslant \delta $. Требуется определить устойчивые приближенные решения ${{x}^{\delta }}$ по заданной приближенной информации ${{y}^{\delta }}$. Во многих приложениях обратные задачи являются некорректно поставленными. Применим метод регуляризации Тихонова [7]. Минимизируемый функционал определен в видеОценка влияния зашумленности входной информации на устойчивость решения обратных задач требует специальных исследований [12].
Возможные подходы к решению обратной задачи коррекции параметров объекта основаны на минимизации квадратичной функции рассогласования или минимизации максимальной из функций рассогласования составляющих сравниваемых собственных спектров – текущего, определяемого переменными модели, и заданного. Для попарно сравниваемых спектральных составляющих можно построить конечное множество критериев рассогласования
В обобщение постановок обратных задач коррекции параметров исследуемого объекта, рассматривается задача глобальной оптимизации, формулируемая в виде: найдем
где(5)
$D = \{ x \in {{{\text{R}}}^{n}}:{\text{ }}{{a}_{j}} \leqslant {{x}_{j}} \leqslant {{b}_{j}},{\text{ }}j \in J\} ,$4. К настоящему времени разработаны и находят многочисленные применения эффективные методы глобальной оптимизации. Обзор современных детерминированных методов глобальной оптимизации дан в работе [13]. Эффективность детерминированных алгоритмов существенно ограничена их зависимостью от размерности задачи. В случае большого числа переменных применяют алгоритмы стохастической глобальной оптимизации. Кратный алгоритм столкновения частиц M-PCA (Multi-Particle Collision Algorithm) основан на алгоритме Метрополиса и входит в число наиболее мощных современных стохастических алгоритмов глобальной оптимизации [14]. Применение стохастических алгоритмов глобальной оптимизации требует значительных вычислительных ресурсов. Одним из путей повышения эффективности таких алгоритмов является совершенствование процедуры локального поиска. Этот подход реализуют при разработке гибридных алгоритмов глобальной оптимизации. Например, гибридный алгоритм HJPCA объединяет стохастический алгоритм столкновения частиц PCA, используемый для сканирования пространства переменных, и детерминированный алгоритм локального поиска методом Хука–Дживса [15]. Описание других гибридных алгоритмов глобальной оптимизации приведено в работе [16].
Структуры гибридных алгоритмов глобальной оптимизации, построены на основе стохастических алгоритмов M-PCA и CBM-PCA (кратного алгоритма столкновения частиц с централизованной выборкой) [17]. Работа алгоритма M-PCA основана на использовании аналогии с процессами абсорбции и рассеяния частиц при ядерных реакциях. В его простейшей версии для исследования области поиска используется одна частица: указанная версия алгоритма M-PCA совпадает с алгоритмом PCA, интегрированным в гибридный алгоритм HJPCA. На начальном шаге выбирается пробное решение (Old_Config), которое затем модифицируется посредством стохастического возмущения (Perturbation), что позволяет найти новое решение (New_Config). С помощью функции Fitness дается сравнительная оценка нового и предыдущего решений, на основании которой новое решение можно принять или отвергнуть. Если новое решение отвергнуто, то происходит переход к функции Scattering, реализующей схему Метрополиса. Для сканирования области, перспективной на минимум, применяются функции Perturbation и Small_Perturbation. Эффективность описанного поиска глобального решения алгоритмом значительно повышается за счет одновременного использования большого числа частиц. Такой подход реализует алгоритм M-PCA, который непосредственно ориентирован на применение в среде параллельных вычислений. Наилучшее решение определяется с учетом данных о всех частицах, участвующих в процессе.
В работе [15] приведены результаты сравнения эффективности гибридного алгоритма HJPCA и современных, обладающих высокими характеристиками алгоритмов, реализующих метаэвристики GLOBAL и C-GRASP [18]. По результатам сравнения алгоритма C-GRASP с генетическим алгоритмом Genocop III и алгоритмами, реализующими метаэвристики Scatter Search и DTSASP, установлено, что при решении сорока стандартных эталонных тестовых задач глобальной оптимизации алгоритм C-GRASP оказался более эффективным. По результатам тестирования гибридного алгоритма HJPCA, а также алгоритмов GLOBAL и C-GRASP (данные получены для четырнадцати стандартных эталонных тестовых многомерных функций), установлена более высокая эффективность алгоритма HJPCA. При использовании алгоритма HJPCA среднее количество вычислений значений критериальных функций составило 14.5% относительно алгоритма C-GRASP.
Реализованы новые гибридные алгоритмы, интегрирующие алгоритм CBM-PCA и детерминированные методы локальной минимизации. Первый предложенный гибридный алгоритм CBM-PCAHJ объединяет стохастический алгоритм CBM-PCA (сканирование пространства переменных) и метод Хука–Дживса (локальный поиск). Второй гибридный алгоритм CBM-PCALMSI интегрирует стохастический алгоритм CBM-PCA и детерминированный метод линеаризации для сглаживающих аппроксимаций критериальных функций LMSI [19]. Благодаря более эффективному сканированию пространства переменных новый гибридный алгоритм CBM-PCAHJ является более мощным по сравнению с алгоритмом HJPCA. Аналогичная оценка эффективности справедлива и в отношении второго предложенного здесь алгоритма CBM-PCALMSI.
5. Рассмотрим обратную задачу коррекции параметров ракеты пакетной схемы по измеряемым модальным данным. Предположим, что экспериментальное определение собственных форм не обеспечивает требуемой точности, поэтому регистрируемые модальные данные представлены только ограниченным собственным спектром, соответствующим ${{n}_{p}}$ низшим собственным частотам объекта. Входная информация моделируется решением прямой задачи для объекта при значениях коэффициентов жесткости узлов межблочных связей: $c_{x}^{в}$ = 0; $c_{y}^{{\text{в}}}$ = 0.3 ⋅ 10–7 Н/м; $c_{z}^{{\text{в}}}$ = 0.4 ⋅ 10–7 Н/м; $c_{x}^{{\text{н}}}$ = = 0.6 ⋅ 10–7 Н/м; $c_{y}^{{\text{н}}}$ = 0.35 ⋅ 10–7 Н/м; $c_{z}^{{\text{н}}}$ = 0.45 ⋅ 10–7 Н/м. Задано ${{n}_{p}} = 48$, при этом учитываются собственные частоты колебаний в интервале до 65 Гц. Предположим, что относительная погрешность входных данных не превышает 0.01%, шумы отсутствуют. Переменные модели представлены вектором $x \in {{{\text{R}}}^{5}}$, определяющим относительные (в %) значения жесткостных характеристик межблочных связей: $0 \leqslant {{x}_{i}} \leqslant 100\% $, $i = \overline {1,{\text{ }}5} $. Критериальная функция обратной задачи определена в виде
Численное решение задачи минимизации критериальной функции $F(x)$ получено с использованием гибридного алгоритма CBM-PCAHJ. После определения области, перспективной на глобальный минимум, локальный поиск реализуется методом Хука–Дживса. Изменение переменных модели ${{x}_{i}}$, $i = \overline {1,{\text{ }}5} $, при возрастании числа итераций в завершающей фазе локального поиска показано на рис. 2; соответствующее изменение значений критериальной функции представлено на рис. 3.
Рис. 2.
Изменение переменных модели ${{x}_{i}}$, $i = \overline {1,{\text{ }}5} $, с ростом числа итераций в завершающей фазе локального поиска.
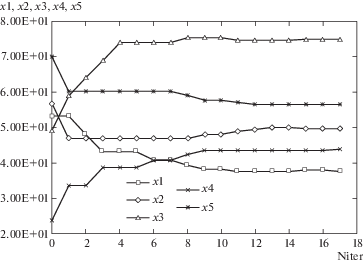
Рис. 3.
Изменение критериальной функции $F(x)$ с ростом числа итераций в завершающей фазе локального поиска.
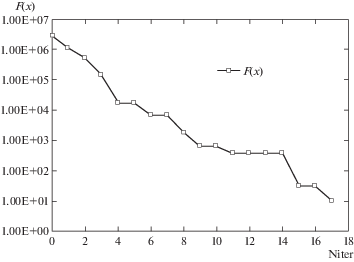
По завершении семнадцати итераций получено $F({{x}^{{17}}}) \approx 9.9263$; целевые $x_{i}^{*}$ и вычисленные приближенные $x_{i}^{{17}}$, $i = \overline {1,{\text{ }}5} $, значения переменных модели приведены в табл. 2.
Таблица 2
| Номер элемента вектора $x$, $i$ | $x_{j}^{*}$,% | $x_{i}^{{17}}$,% |
|---|---|---|
| 1 | 37.5 | 37.603 |
| 2 | 50.0 | 49.717 |
| 3 | 75.0 | 75.024 |
| 4 | 43.75 | 43.713 |
| 5 | 56.25 | 56.469 |
Значения жесткостных характеристик межблочных связей, восстановленные по приближенным значениям переменных модели, соответственно равны: $c_{y}^{{\text{в}}} \approx 0.300824 \cdot {{10}^{{ - 7}}}$ Н/м; $c_{z}^{{\text{в}}} \approx 0.39774 \cdot {{10}^{{ - 7}}}$ Н/м; $c_{x}^{{\text{н}}} \approx 0.{\text{60019}} \cdot {{10}^{{ - 7}}}$ Н/м; $c_{y}^{{\text{н}}} \approx 0.34970 \cdot {{10}^{{ - 7}}}$ Н/м; $c_{z}^{{\text{н}}} \approx 0.45175 \cdot {{10}^{{ - 7}}}$ Н/м. Наибольшая относительная погрешность решения (определяется восстановленным значением параметра $c_{z}^{в}$) здесь не превышает 0.57%. Можно отметить достаточную согласованность точности полученного приближенного решения модельной задачи и заданной входной информации.
Заключение. Представлена методика коррекции параметров ракеты пакетной схемы по модальным данным. Для математической модели объекта решение прямой задачи получено методом итерации подпространства. Сформулирована обратная задача коррекции параметров объекта, при решении которой используется оптимизационный подход. Предложены два новых гибридных алгоритма глобальной оптимизации. По результатам косвенных оценок установлена достаточно высокая эффективность предложенных алгоритмов. Решение модельной задачи коррекции жесткостных характеристик узлов межблочных связей по модальным данным получено с использованием гибридного алгоритма CBM-PCAHJ. Точность полученного приближенного решения согласована с точностью задания входной информации.
Конфликт интересов. Авторы заявляют об отсутствии конфликта интересов.
Список литературы
Колесников К.С. Динамика ракет: Учебник для вузов. 2-е изд. М.: Машиностроение, 2003. С. 520.
Pulecchi T., Casella F., Lovera M. Object-oriented modelling for spacecraft dynamics: Tools and applications // Simulation Modelling and Theory. 2010. V. 18. № 1. P. 63.
Колесников К.С., Пожалостин А.А., Шкапов П.М. Задачи динамики гидромеханических систем в трудах кафедры теоретической механики имени профессора Н.Е. Жуковского // Инженерный журнал: наука и инновации. 2012. № 7. С. 16
Lee E.-T., Eun H.-C. Update of corrected stiffness and mass matrices based on measured dynamic modal data // Applied Mathematical Modelling. 2009. V. 33. № 5. P. 2274.
Разработка расчетно-экспериментального метода модального анализа крупногабаритных трансформируемых космических конструкций / В.А. Бернс, В.Е. Левин, Д.А. Красноруцкий, Д.А. Маринин, Е.П. Жуков, В.В. Маленкова, П.А. Лакиза // Космические аппараты и технологии. 2018. Т. 2. № 3. С. 125.
Yuan Y., Liu H. An iterative updating method for damped structural systems using symmetric eigenstructure assignment // Journal of Computational and Applied Mathematics. 2014. V. 256. P. 268.
Benning M., Burger M. Modern regularization methods for inverse problems // Acta Numerica. 2018. V. 27. P. 1.
Bartilson D.T., Jang J., Smyth A.W. Finite element model updating using objective-consistent sensitivity-based parameter clustering and Bayesian regularization // Mechanical Systems and Signal Processing. 2019. V. 114. P. 328.
Structural damage detection using finite element model updating with evolutionary algorithms: a survey / N.F. Alkayem, M. Gao, Y. Zhang, M. Bayat, Z. Su // Neural Computing and Applications. 2018. V. 30. P. 389.
Колесников К.С. Жидкостная ракета как объект регулирования. М.: Машиностроение, 1969. С. 298.
Tang F.T.P., Polizzi E. FEAST as a subspace iteration eigensolver accelerated by approximate spectral projection // SIAM Journal on Matrix Analysis and Applications. 2014. V. 35. № 2. P. 354.
Bleyer I.R., Ramlau R. A double regularization approach for inverse problems with noisy data and inexact operator // Inverse Problems. 2013. V. 29. 025004 P. 16.
Floudas C.A., Gounaris C.E. A review of recent advances in global optimization // Journal of Global Optimization. 2009. V. 45. № 1. P. 3.
Luz E.F.P., Becceneri J.C., de Campos Velho H.F. A new multi-particle collision algorithm for optimization in a high performance environment // Journal of Computational Interdisciplinary Sciences. 2008. V. 1. P. 3.
Rios-Coelho A.C., Sacco W.F., Henderson N.A. Metropolis algorithm combined with Hooke-Jeeves local search method applied to global optimization // Applied Mathematics and Computation. 2010. V. 217. № 2. P. 843.
A hybrid approach to constrained global optimization / J. Liu, S. Zhang, C. Wu, J. Liang, X. Wang, K.L. Teo // Applied Soft Computing. 2016. V. 47. P. 281.
Torres R.H., da Luz E.F.P., de Campos Velho H.F. Multi-particle collision algorithm with reflected points // Proceeding Series of the Brazilian Society of Applied and Computational Mathematics. 2015. V. 3. № 1. 010433. P. 6.
Hirsch M.J., Pardalos P.M., Resende M.G.C. Speeding up continuous GRASP // European Journal of Operational Research. 2010. V. 205. № 3. P. 507.
Sulimov V.D., Shkapov P.M., Sulimov A.V. Jacobi stability and updating parameters of dynamical systems using hybrid algorithms // IOP Conference Series: Materials Science and Engineering. 2018. № 468. 012040. P. 11.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин