Проблемы машиностроения и надежности машин, 2019, № 7, стр. 54-63

1. Введение. Крупногабаритные емкости для хранения и транспортировки сжиженных газов находят широкое распространение в различных областях техники. Сжиженный природный газ [1], основную долю которого составляет метан, является перспективным горючим для двигателей летательных аппаратов [2]. Для жидкостных ракетных двигателей в качестве окислителя и горючего используют соответственно жидкие кислород и водород [3, 4]. Процессы заполнения или захолаживания криогенной емкости низкотемпературной жидкостью, регламентированные перед заполнением емкости [5], связаны с возникновением в ее оболочке неравномерного распределения температуры. В силу существенного различия интенсивности теплообмена с жидкой и газообразной фазами наиболее резко изменяется температура оболочки в зоне уровня криогенной жидкости (как подвижного, так и неподвижного).

Одним из распространенных вариантов крупногабаритных криогенных емкостей являются топливные баки первых ступеней жидкостных ракет-носителей, основным конструктивным элементом которых является тонкостенная круговая цилиндрическая оболочка [4, 6]. Неравномерное распределение температуры в окрестности уровня криогенной жидкости вызывает искривление образующей такой оболочки и снижает ее сопротивление действию приложенной осевой сжимающей нагрузки. В данной статье с использованием результатов математического моделирования термонапряженного состояния цилиндрической оболочки криогенного бака при его заполнении [7–9] получены соотношения, позволяющие оценить допустимую осевую нагрузку на оболочку, при которой ее материал остается в пределах линейно-упругой области.

2. Температурное состояние оболочки. При заполнении вертикально расположенного цилиндрического криогенного бака на температурное состояние его оболочки влияют ряд факторов. Среди них скорость подъема уровня жидкости и интенсивность теплообмена на смоченном и несмоченном участках внутренней поверхности оболочки, определяемые соответственно коэффициентом теплообмена ${{\alpha }_{1}}$ с жидкостью, имеющую температуру $T_{1}^{*}$, и коэффициентом теплообмена ${{\alpha }_{2}}$ с имеющей температуру $T_{2}^{*}$ газовой средой в полости бака над уровнем жидкости.

Для уменьшения подвода теплоты от внешней среды и снижения потерь криогенной жидкости при заполнении бака внешнюю поверхность его оболочки можно покрыть слоем малотеплоемкой теплоизоляции с коэффициентом теплопроводности $\lambda {\kern 1pt} {\text{'}}$ и толщиной $h{\kern 1pt} '$. Например, оболочка топливного бака многоразовой космической системы Space-Shattle [6] была покрыта слоем пенополиуретана, что предотвращает образование инея и наледи на внешней поверхности бака в период его заполнения. При наличии внешнего слоя теплоизоляции эффективное значение коэффициента теплообмена оболочки с внешней средой определяет равенство ${{\alpha }_{3}} = 1{\text{/}}(1{\text{/}}\alpha _{3}^{'} + h{\kern 1pt} '{\text{/}}\lambda {\kern 1pt} ')$, где $\alpha _{3}^{'}$ – коэффициент теплообмена поверхности теплоизоляции с внешней средой, имеющей температуру $T_{3}^{*}$.

Если в качестве материала оболочки бака использовать достаточно теплопроводный материал (например, алюминиевый сплав АМг6 с коэффициентом теплопрводности $\lambda = 122$ Вт/(м ⋅ К) [10]), то изменением температуры по толщине $h$ оболочки можно пренебречь. Тогда при наличии осевой симметрии конструкции бака достаточно учитывать зависимость температуры оболочки лишь от времени $t$ и координаты $x$, отсчитываемой от уровня криогенной жидкости вверх вдоль образующей оболочки. В окрестности уровня жидкости распределение температуры в оболочке удовлетворяет условиям непрерывности [7]

где ${{T}_{1}}(x,t)$ и ${{T}_{2}}(x,t)$ – распределения температуры соответственно в уже смоченных и еще несмоченных участках оболочки.

При наличии внешнего слоя теплоизоляции с удельной объемной теплоемкостью $c{\kern 1pt} '$ справедливо неравенство $h{\text{'}}c{\text{'}} \ll hc$, где $c$ – удельная объемная теплоемкость материала оболочки. Поэтому влиянием теплоемкости этого слоя можно пренебречь. Тогда при движении уровня жидкости вверх со скоростью $v$ распределения температуры участков оболочки будут удовлетворять, согласно закону сохранения тепловой энергии, дифференциальным уравнениям [8] (аргументы функций ${{T}_{1}}(x,t)$ и ${{T}_{2}}(x,t)$ опущены)

По мере удаления от уровня жидкости неравномерность распределения температуры вдоль образующей оболочки будет убывать. Тогда помимо условий непрерывности (1) для уравнений (2) и (3) можно задать еще два граничных условия

Если условия теплообмена не зависят от времени, а уровень жидкости неподвижен $(v = 0)$, то распределение температуры в оболочке будет стремиться при $t \to \infty $ к некоторому установившемуся температурному состоянию, для которого из уравнений (2) и (3) при $t \to \infty $ следуют условия

Это состояние в момент начала движения уровня жидкости определит начальное условие для уравнений (2) и (3) при $v > 0$.

При независимых от $t$ и $x$ параметрах теплообмена и постоянной скорости движения уровня жидкости левые части соотношений (2), (3) при $t \to \infty $ стремятся к нулю. В этом случае соотношения (2), (3) перейдут в обыкновенные дифференциальные уравнения второго порядка [9]

где $a = \lambda {\text{/}}c$ – коэффициент температуропроводности материала оболочки, ${{H}_{1}} = ({{\alpha }_{1}} + {{\alpha }_{3}}){\text{/}}\lambda $, ${{H}_{2}} = ({{\alpha }_{2}} + {{\alpha }_{3}}){\text{/}}\lambda $. Эти уравнения с учетом граничных условий вида (1) и (4) имеют решения [10, 11] Здесь ${{K}_{1}} = \sqrt {{{V}^{2}} + H_{1}^{2}} + V$, ${{K}_{2}} = \sqrt {{{V}^{2}} + H_{2}^{2}} - V$, $V = v{\text{/}}(2a)$. Соотношения (5) описывают квазистационарное распределение температуры в оболочке. При $x = 0$ на границе между смоченной и несмоченной участками поверхности оболочки ее температура равна ${{T}_{0}} = {{\tilde {T}}_{1}} + ({{\tilde {T}}_{2}} - {{\tilde {T}}_{1}}){\text{/}}(1 + {{K}_{1}}{\text{/}}{{K}_{2}})$.

Из формул (5) в силу $exp( - 3) \approx 0.05$ следует, что неравномерность квазистационарного распределения температуры в первом приближении достаточно учитывать лишь при $x \in ( - 3{\text{/}}{{K}_{1}},3{\text{/}}{{K}_{2}})$. За пределами этого промежутка температуру смоченной и несмоченной частей оболочки можно принять равными ${{\tilde {T}}_{1}}$ и ${{\tilde {T}}_{2}}$ соответственно. При $v \approx 10$ мм/с переход от однородного начального распределения температуры к квазистационарному в оболочке толщиной не более 10 мм, выполненной из сплава АМг6 (при этом $2hV \approx 1$), можно считать практически завершенным за период времени, не превышающий 10 с [9].

При неподвижном уровне жидкости температуру всего смоченного участка оболочки в первом приближении можно положить равной температуре жидкости, т.е. принять ${{T}_{1}}(x) \approx {{\tilde {T}}_{1}} \approx T_{1}^{*}$ [7], т.к. отношение ${{\alpha }_{1}}{\text{/}}{{\alpha }_{2}}$ велико благодаря высокой интенсивности теплообмена на смоченной поверхности оболочки, а значения ${{\alpha }_{2}}$ и ${{\alpha }_{3}}$ обычно сопоставимы между собой [8].

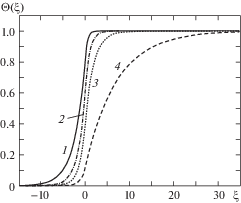
На рис. 1 приведены распределения безразмерной температуры Θ(ξ)  = $\Theta (\xi ) = (T(\xi ) - {{\tilde {T}}_{1}}){\text{/}}({{\tilde {T}}_{2}} - {{\tilde {T}}_{1}})$ в зависимости от безразмерной координаты $\xi = x{\text{/}}h$ при фиксированных значениях параметров ${{\tilde {H}}_{1}} = {{H}_{1}}h = 1$, ${{\tilde {H}}_{2}} = {{H}_{1}}h = 0.02$ и различных значениях параметра $\tilde {V} = Vh$, в том числе при $\tilde {V} = 0$, что соответствует неподвижному уровню жидкости (5).

3. Радиальное перемещение оболочки. В силу температурного расширения материала оболочки неравномерное распределение температуры вдоль образующей криогенного бака (5) вызывает радиальное перемещение оболочки. Непосредственным влиянием внутреннего давления в баке, избыточного по отношению к давлению окружающей среды, можно пренебречь, поскольку при заполнении бака с открытым дренажным клапаном [5] давление ${{p}_{0}}$ в полости бака над уровнем жидкости может превышать давление окружающего бак воздуха не более, чем на 0.2 МПа [11]. Гидростатической составляющей давления на смоченной части оболочки водородного бака также можно пренебречь в силу малой плотности жидкого водорода. Для бака с жидкими кислородом или метаном, плотности которых соответственно 1136 кг/м³ и 426 кг/м³ [12] при стандартном атмосферном давлении 101.3 кПа и температуре кипения, это давление более существенно, но его влияние будет заметно лишь на глубине за пределами области краевого эффекта в окрестности уровня жидкости.

При анализе радиального перемещения оболочки помимо распределения температуры вдоль образующей бака достаточно учитывать лишь влияние осевой сжимающей силы $P$ и разгружающий эффект давления ${{p}_{0}}$, определяемый в первом приближении силой ${{P}_{1}} = \pi \,{{R}^{2}}{{p}_{0}}$, где $R$ – радиус средней поверхности оболочки.

При линейно-упругом поведении материала осесимметричной оболочки отнесенные к ее средней поверхности погонные усилия ${{N}_{\theta }}$ и ${{N}_{y}}$ соответственно в меридиональном и окружном направлениях представим в виде [7, 9]

где ${{\tilde {\varepsilon }}_{T}} = {{\alpha }_{T}}(T - {{\tilde {T}}_{1}})$ – температурная деформация, $E$, $\nu $ и ${{\alpha }_{T}}$ – продольный модуль упругости (модуль Юнга), коэффициент Пуассона и температурный коэффициент линейного расширения материала оболочки, ${{\varepsilon }_{\theta }}$ и ${{\varepsilon }_{y}} = w{\text{/}}R$ – деформации средней поверхности соответственно в меридиональном и окружном направлениях, $w$ – перемещение средней поверхности в радиальном направлении.

Приложенной к верхнему торцу оболочки осевой сжимающей силе $P$ и разгружающей силе ${{P}_{1}}$ отвечает сжимающая погонная нагрузка $N = (P - {{P}_{1}}){\text{/}}(2\pi R)$. С учетом этой нагрузки условие равновесия оболочки в радиальном направлении в линейном приближении имеет вид [10]

где ${{M}_{x}} = D({{d}^{2}}w{\text{/}}d{{x}^{2}} - \nu w{\text{/}}{{R}^{2}})$ – погонный изгибающий момент в поперечном сечении оболочки, $D = (E{{h}^{3}}{\text{/}}12){\text{/}}(1 - {{\nu }^{2}})$ – цилиндрическая погонная жесткость оболочки на изгиб. В силу неравенства ${\text{|}}{{d}^{2}}w{\text{/}}d{{x}^{2}}{\text{|}} \gg {\text{|}}\nu w{\text{/}}{{R}^{2}}{\text{|}}$ влияние изменения кривизны оболочки в окружном направлении можно не учитывать.

Исключив из соотношений (6) деформацию ${{\varepsilon }_{\theta }}$ получим

После подстановки формул для ${{M}_{x}}$ и ${{N}_{y}}$ в уравнение (7) с учетом приближенного равенства ${{N}_{\theta }} \approx - N$ запишем

Здесь $4{{\beta }^{2}} = 2\sqrt {EhD} {\text{/}}R + N{\text{/}}D$ и $4{{\gamma }^{2}} = 2\sqrt {EhD} {\text{/}}R - N{\text{/}}D$. Обыкновенное дифференциальное уравнение (9) четвертого порядка описывает краевой эффект в окрестности уровня жидкости с учетом отклонения образующей осесимметричной оболочки криогенного бака от прямолинейной формы.

Характеристическое уравнение, соответствующее однородной части уравнения (9), имеет две пары комплексно сопряженных корней $\gamma \pm \beta i$ и $ - \gamma \pm \beta i.$ Вне зоны краевого эффекта функция $w\,(x)$ должна совпадать с частным решением $w_{{}}^{*}(x)$ уравнения (9), а общее решение соответствующего однородного уравнения при ${\text{|}}x{\text{|}} \to \infty $ должно убывать по абсолютному значению и стремиться к нулю. Этому условию при $x < 0$ удовлетворяет лишь первая пара корней и общим решением однородного уравнения будет соотношение

а при $x > 0$ удовлетворяет лишь вторая пара корней, так что общее решение примет вид

Обозначенные литерой $C$ постоянные коэффициенты в равенствах (10) и (11) определим с учетом частных решений уравнения (9) из условия непрерывности при $x = 0$ функции $w\,(x)$ и первых трех ее производных.

При квазистационарном распределении температуры, описываемым соотношениями (5), частными решениями уравнения (9) будут при $x < 0$

где ${{w}_{T}} = {{\alpha }_{T}}({{\tilde {T}}_{2}} - {{\tilde {T}}_{1}})R$ и $B{\kern 1pt} ' = K_{1}^{4} + 2(\beta _{0}^{2} - \gamma _{0}^{2})K_{1}^{2} + {{(\beta _{0}^{2} + \gamma _{0}^{2})}^{2}}$, а при $x > 0$ – где $B{\kern 1pt} '{\kern 1pt} ' = K_{2}^{4} + 2(\beta _{0}^{2} - \gamma _{0}^{2})K_{1}^{2} + {{(\beta _{0}^{2} + \gamma _{0}^{2})}^{2}}$.

Общее решение ${{w}^{{^{ \circ }}}}(x) + {{w}^{*}}(x)$ уравнения (9) и первые три производные этого решения должны удовлетворять при $x = 0$ условиям непрерывности, что с учетом равенств (10)–(13) приводит к системе линейных алгебраических уравнений

где

Решением системы уравнений (14) будут равенства

В итоге для неоднородного уравнения (9) общее решение ${{w}_{1}}(x) = w_{1}^{{^{ \circ }}} + w_{1}^{*}(x)$ при x < 0 определяем равенствами (10), (12), а общее решение ${{w}_{2}}(x) = w_{2}^{{^{ \circ }}} + w_{2}^{*}(x)$ при x > 0 – равенствами (11), (13).

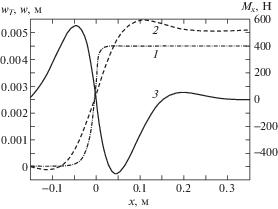
Полученные соотношения использованы для построения графиков зависимостей (рис. 2) от координаты $x$ температурного приращения $w_{T}^{'} = {{\varepsilon }_{T}}R$ радиуса оболочки, ее полного радиального перемещения $w$ и осевого погонного изгибающего момента $M$ при заполнении криогенного бака жидким кислородом. В расчетах принято: h = 0.005 м; R = 1 м; ${{\tilde {T}}_{2}} - {{\tilde {T}}_{1}} = 182$ К; $v = 0.01$ м/с; ${{H}_{1}}h = 0.5$; ${{H}_{2}}h = 0.01$, $N = 3 \cdot {{10}^{5}}$ Н/м; материал оболочки – алюминиевый сплав АМг6, для которого $\lambda = 122$ Вт/(м ⋅ К), $a = 5 \cdot {{10}^{{ - 5}}}$ м²/с, E = 71 ГПа, $\nu = 0.31$ и ${{\alpha }_{T}} = 24.7 \cdot {{10}^{{ - 6}}}$ 1/К.

4. Напряженное состояние оболочки. Определитель матрицы системы уравнений (14) обращается в нуль при значении ${{N}_{{cr}}} = (2{\text{/}}R)\sqrt {DEh} $, т.е. при верхнем значении критического погонного усилия, соответствующего потере устойчивости достаточно длинной цилиндрической линейно-упругой оболочки, сохраняющей в докритическом напряженном состоянии прямолинейность образующей [13, 14]. Значению ${{N}_{{cr}}}$ отвечает критическое значение осевого сжимающего напряжения ${{\sigma }_{{cr}}} \approx 0.605{\kern 1pt} Eh{\text{/}}R$ [7], т.е. эта формула применима лишь при условии $h{\text{/}}R < 1.65{\kern 1pt} {{\sigma }_{Y}}{\text{/}}E$, где ${{\sigma }_{Y}}$ – предел текучести материала оболочки. Для сплава АМг6 при температуре 78 К ${{\sigma }_{Y}} = 185$ МПа и $E = 71$ ГПа [10], т.е. отношение $h{\text{/}}R$ не должно превышать 0.0043, что соответствует весьма тонкостенной оболочке.

Искривление образующей оболочки в зоне подвижного краевого эффекта приводит к возрастанию локальных абсолютных значений напряжений, которые могут превысить предел текучести материала оболочки. При этом известные подходы анализа упругой устойчивости оболочки станут неприменимы. Пластическое деформирование материала оболочки в зоне краевого эффекта, возникающего на стадии заполнения криогенного бака, вызовет остаточное формоизменение, влияющее на несущую способность конструкции на последующих этапах ее эксплуатации. В связи с этим актуальным является анализ напряженного состояния оболочки бака в зоне краевого эффекта с точки зрения возможности выхода материала за пределы области линейной упругости.

В рамках допущения о плоском напряженном состоянии оболочки примем, что линейно-упругое поведение материала согласно критерию Мизеса [7] имеет место при условии

где ${{\sigma }_{i}}$ – интенсивность напряжений, ${{\sigma }_{\theta }}$ и ${{\sigma }_{y}}$ – напряжения в меридиональном и окружном направлениях соответственно. Для обеспечения надежного функционирования рассматриваемой оболочки в пределах линейно-упругой области условие (15) должно быть выполнено с некоторым регламентированным запасом, определяемым коэффициентом при величине ${{\sigma }_{i}}$, превосходящим единицу.

Изменение радиального перемещения средней поверхности оболочки в зоне подвижного краевого эффекта (рис. 2) позволяет заключить, что при фиксированном сжимающем погонном усилии $N$ и примерно равных ближайших к уровню жидкости экстремальных значениях осевого погонного изгибающего момента наибольшие значения ${{\sigma }_{i}}$ будут соответствовать окрестностям точек с абсциссами этих экстремумов на сжатой наружной поверхности смоченной части оболочки и на ее внутренней поверхности несмоченного участка. Осевое сжимающее напряжение в окрестностях этих точек, вызванное осевым погонным изгибающим моментом ${{M}_{x}}$, равно ${{\sigma }_{M}} = - 6\left| {{{M}_{x}}} \right|{\text{/}}{{h}^{2}}$, а осевой сжимающей силой – ${{\sigma }_{N}} = - N{\text{/}}h$. Следовательно, совпадающее в данном случае с меридиональным осевое напряжение, наибольшее по абсолютному значению, определяет равенство $\sigma _{x}^{*} = - \left| {6{{M}_{x}}} \right|{\text{/}}{{h}^{2}} - N{\text{/}}h$. C погонным изгибающим моментом ${{M}_{y}} = \nu {{M}_{x}}$ в окружном направлении связано сжимающее напряжение $\sigma _{y}^{'} = - 6\nu {\text{|}}{{M}_{x}}{\text{|/}}{{h}^{2}}$, а с радиальным перемещением $w$ – напряжение $\sigma _{y}^{{''}} = {{N}_{y}}{\text{/}}h$ (в формуле (8) для ${{N}_{y}}$ следует ${{N}_{\theta }}$ заменить на $ - N$). Значение ${{N}_{y}}$ может быть как положительным, так и отрицательным.

В линейном приближении, пренебрегая величиной ${{(dw{\text{/}}dx)}^{2}}{\text{/}}2$ по сравнению с единицей, в формуле (15) можно заменить напряжения ${{\sigma }_{\theta }}$ и ${{\sigma }_{y}}$ соответственно на $\sigma _{x}^{*}$ и $\sigma _{y}^{*} = \sigma _{y}^{'} + \sigma _{y}^{{''}}$ и использовать при вычислениях формулу

Например, при исходных данных, использованных при построении графиков на рис. 2, сжимающей погонной нагрузке $N = 3 \cdot {{10}^{5}}$ Н/м соответствует составляющая осевого сжимающего напряжения ${{\sigma }_{N}} = - 60$ МПа. На смоченной части оболочки ближайший к уровню жидкости экстремум осевого погонного изгибающего момента является максимумом, равным 551.4 Н. Ему соответствует на внутренней поверхности этого участка сжимающее напряжение ${{\sigma }_{M}} = - 132.3$ МПа. Таким образом, на этой поверхности суммарное сжимающее напряжение имеет значение $\sigma _{x}^{*} = - 192.3$ МПа, которое по абсолютному значению превосходит предел текучести ${{\sigma }_{Y}}$ сплава АМг6. В окружном направлении на этой поверхности в окрестности указанного максимума изгибающего момента имеем $\sigma _{y}^{'} = - 41.0$ МПа и $\sigma _{y}^{{''}} = 24.3$ МПа. В итоге получим $\sigma _{y}^{*} = - 16.7$ МПа и, согласно формуле (16), ${{\sigma }_{i}} = 184.5$ МПа, что практически совпадает с указанным выше пределом текучести.

Аналогичные подсчеты напряжений в окрестности точки ближайщего к уровню жидкости экстремума осевого погонного изгибающего момента на несмоченном участке оболочки приводят к несколько меньшему значению ${{\sigma }_{i}} = 176.5$ МПа. При уменьшении скорости движения уровня жидкости и фиксированном значении погонной силы $N$ интенсивность напряжения ${{\sigma }_{i}}$ возрастает. Основной причиной является более пологое изменение температуры несмоченной части оболочки в окрестности уровня жидкости и, наоборот, более резкое изменение в этой окрестности температуры смоченной части оболочки. Это приводит к увеличению положительного значения ${{N}_{y}}$ и возрастанию ${{\sigma }_{i}}$.

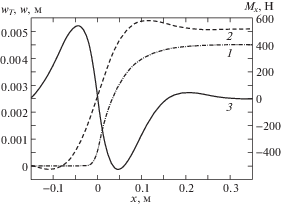
На рис. 3 представлены графики при неподвижном уровне жидкости и прежнем значении $N = 3 \cdot {{10}^{5}}$ Н/м. В этом случае на несмоченной части оболочки наибольшее значение 226.3 МПа интенсивности напряжения превышает предел текучести, но и на смоченной части соответствующее значение 186.1 МПа также несколько выше допустимого. Условие ${{\sigma }_{Y}} > {{\sigma }_{i}}$ на несмоченной части оболочки может быть выполнено лишь при значении $N < 1.74 \cdot {{10}^{5}}$ Н/м.

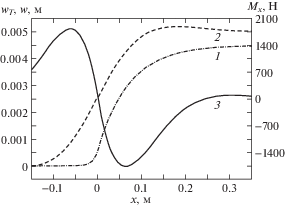
Увеличение толщины оболочки позволяет даже в случае неподвижного уровня жидкости повысить значение $N$ при выполнении условия, определяемого соотношением (15). На рис. 4 приведены графики при толщине h = 0.01 м и прежних остальных исходных данных. Для несмоченной части оболочки выполнению условия ${{\sigma }_{i}} \leqslant {{\sigma }_{Y}} = 185$ МПа соответствует значение $N = 4.27 \cdot {{10}^{5}}$ Н/м. При этом на смоченной части наибольшее значение интенсивности напряжения не превышает 160 МПа. При заполнении бака допустимый уровень осевой сжимающей нагрузки возрастает, но более напряженным становится смоченный участок оболочки вблизи уровня жидкости. При скорости подъема уровня жидкости $v = 0.005$ м/с условие (15) выполнимо, если $N < 6.53 \cdot {{10}^{5}}$ Н/м, а при $v = 0.01$ м/с, если $N < 7.24 \cdot {{10}^{5}}$ Н/м.

Заключение. Количественный анализ комплексной математической модели, описывающей термодеформированное состояние подкрепленной стрингерами оболочки вертикально расположенного цилиндрического криогенного бака при его заполнении, позволяет оценить неравномерность распределения температуры в оболочке и ее радиального перемещения в зоне движущегося уровня криогенной жидкости, а также найти экстремальные значения погонного изгибающего момента. Это дает возможность уточнить постановку и решение задачи об устойчивости оболочки бака при действии осевой сжимающей нагрузки.

Полученные соотношения можно применить и для оценки допустимой нагрузки в случае оболочки бака, подкрепленной силовым набором (достаточно часто расположенными стрингерами и кольцевыми ребрами или вафельным подкреплением [15]), если привести характеристики жесткости такой оболочки к ее некоторой условной средней поверхности [16].

Конфликт интересов. Авторы заявляют, что у них нет конфликта интересов.