Проблемы машиностроения и надежности машин, 2020, № 1, стр. 3-10

1. Постановка задачи. Метод определения момента инерции тела по периоду его колебаний, как физического маятника, совместно с методом пробных грузов, применяемым при балансировке роторов, широко используют для экспериментального определения масс и моментов инерции тел [1–10]. Возможности такого совместного технологического приема можно значительно расширить и определять одновременно не только массу и момент инерции, но и координаты центра масс, а также тензор инерции тела для широкой номенклатуры изделий, прочностные свойства которых не позволяют им испытывать динамические перегрузки при испытаниях. Это относится к тонкостенным корпусным деталям авиационных и машиностроительных конструкций, пространственным фермам, уникальным объектам зоологической природы. Проблема в том, что если к исследуемому объекту не применима модель твердого тела из-за его деформаций в процессе навязанных ему колебаний, то он сам становится колебательным звеном в измерительной цепи. В результате образуется сложная колебательная система, в которой увеличиваются динамические погрешности измерений инерционных характеристик.

В качестве альтернативы широко применяемым в настоящее время колебательным процессам, сообщаемым исследуемому телу, известен метод определения массы и координат центра масс тела в заданной плоскости, основанный на сообщении вращательного движения [11].

Однако применяемый в этом методе технологический прием задавать телу и пробному грузу конечные линейные перемещения при вращательном движении, позволяет определять только массу тела и две координаты центра масс в заданной плоскости. Положение центра масс в пространстве остается неизвестным. Невозможно также определить компоненты тензора инерции.

2. Решение задачи. Предлагается дополнительно, кроме линейных перемещений, задаваемых телу и пробному грузу в плоскости вращения, сообщать им последовательно, угловые повороты на 45° и 90° градусов относительно специально выбранных осей. В каждом новом фиксированном угловом положении тела и пробного груза, по-разному проявляются их инерционные свойства, вызванные вращательным движением. Измеряемая реакция динамической системы стенда на ряд заданных угловых ориентаций тела и пробного груза в пространстве содержит достаточную информацию для определения тензора инерции и координат центра масс в пространстве.

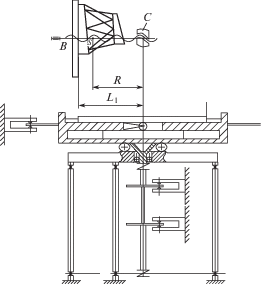
Для выполнения заданных линейных и угловых перемещений разработан манипулятор (рис. 1).

Исследуемое тело 1 установлено на планшайбе 2, которая может поворачиваться относительно кронштейна 3 на углы 45° и 90° градусов вокруг оси В и фиксироваться в каждом из этих положений. Кронштейн 3 вместе с двумя винтовыми механизмами 4, работающими всегда синхронно, образуют поворотный механизм вокруг оси С на углы 45° и 90°. Вся конструкция манипулятора базируется на каретке 5, которая может перемещаться в радиальном направлении в плоскости платформы 6 с помощью привода (на рис. 1 привод не показан). Это линейное конечное перемещение необходимо для нахождения координат центра масс. Механизм манипулятора обеспечивает три степени свободы: поворот вокруг осей В и С, а также линейное смещение за счет вращения винтовых механизмов 4. С помощью этих механизмов центр масс S тела может быть совмещен с осью С. Вся процедура определения инерционных характеристик состоит из двух, последовательно выполняемых этапов: определение массы и координат центра масс в пространстве; определение тензора инерции.

Полагаем, что масса и две координаты центра масс в плоскости планшайбы уже определены, согласно методике [11].

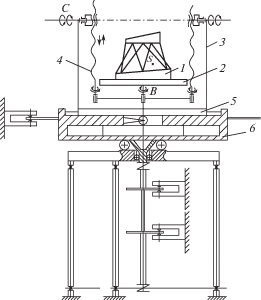
Для определения третьей координаты, совмещаем центр масс S с осью В с помощью перемещения тела на планшайбе. Затем повернув механизм манипулятора вокруг оси С на 90°, центр S располагаем в горизонтальной плоскости, проходящей через ось С (рис. 2). Пользуясь известным методом [11], находим расстояние R от оси вращения до центра масс. Зная R, определяем третью координату центра масс S относительно плоскости планшайбы, как разность: L₁– R. С помощью механизма 4 (рис. 1) совмещаем центр масс S с осью С. Центр масс S находится в точке пересечения осей В и С (рис. 3).

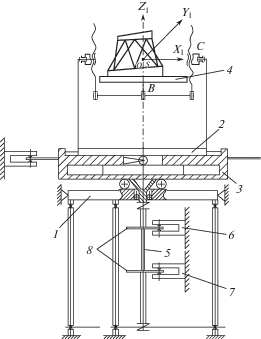
С изделием в центре масс S связываем систему координат OX₁Y₁Z₁. В начальном положении ось OX₁ совмещена с осью С, а ось OZ₁ – c осью В.

Повороты на 45° и 90°, задаваемые манипулятором телу и системе координат OX₁Y₁Z₁, позволяют определить известным методом [12] шесть компонент тензора инерции.

В основе метода лежит известная теорема М.М. Гернет о соотношениях между шестью осевыми и тремя центробежными моментами инерции при специальном выборе координатных осей, относительно которых определяют шесть осевых моментов инерции. Это три координатные оси системы OX₁Y₁Z₁, а также три биссектрисы прямых углов, образованных этими осями: ось U – биссектриса угла X₁OZ₁, ось V – биссектриса угла X₁OY₁; ось W – биссектриса угла Y₁OZ₁.

Для определения шести осевых центральных моментов инерции относительно указанных осей необходимо каждую из них совместить с осью вращения. Для этого основание 1 стенда закрепляется неподвижно (рис. 3), а каретка 2 находится в центральном положении и ось В совпадает с осью вращения платформы 3. Сообщая планшайбе 4 последовательно повороты вокруг осей В и С, можно каждую из шести координатных осей совместить с осью вращения платформы. Например, для совмещения оси ОX₁ необходимо планшайбу 4 повернуть вокруг оси В на 90°, а затем на 90° вокруг оси С. Задавая изделию ускоренное вращение и измеряя крутящий момент М, угловую скорость ω и угол поворота φ, по теореме об изменении кинетической энергии Т = Jω²/2, можно рассчитать осевой момент инерции J вращающихся масс относительно каждой из шести осей из уравнения

где ${{M}_{r}}$ – момент сопротивления вращению в опорах качения стенда.

Уравнение (1) может быть сведено к интегралу, если все входящие функции будут зависеть от одного аргумента φ. Для этого измерительная система стенда разработана так, что функции ω, М и ${{M}_{r}}$ определяются экспериментально, как функции одного аргумента φ, (рис. 3). Крутящий момент М от двигателя передается платформе 3 через торсионный вал 5 с известной угловой жесткостью j. На концах торсиона 5 расположены два фотоэлектрических датчика 6 и 7 для измерения угла поворота платформы 3, угла закручивания ψ торсиона 5 и расчета крутящего момента М = jψ – как функции угла φ [13]. Датчик 6 измеряет угол поворота φ платформы 3 и ее угловую скорость ω, как функцию φ: ${\omega (}{{{\varphi }}_{k}})$ = $\frac{{\Delta {\varphi }}}{{\Delta {{t}_{k}}}}$ (k = 1, 2, …, N), где Δφ – шаг следования отверстий, модулирующих световой поток на подвижных дисках 8. Интервал времени Δt_k измеряется таймером по командам датчика 6. Погрешность измерения интервала Δt_k фотоэлектрическим методом не более 10^–7 с [13].

Для любого положения планшайбы 4 в пространстве, осевой момент инерции J_i вращающихся деталей стенда всегда может быть рассчитан и поэтому известен (i = 1, 2, 3). Интегрируя уравнение (1) для шести угловых положений тела, получим шесть уравнений баланса энергий

где J_i – известные осевые моменты инерции деталей стенда для трех угловых положений планшайбы 2 при поворотах вокруг оси С; J_X, J_Y…J_W – определяемые осевые моменты инерции тела.

В каждом из шести уравнений содержатся по два неизвестных: момент инерции тела и величина работы момента сил трения $\sum\nolimits_{{{\varphi }_{m}}}^{{{\varphi }_{n}}} {{{M}_{r}}(\varphi ,\omega (\varphi ))\Delta \varphi } $ на отрезке [φ_m, φ_n], т.е. система из шести уравнений содержит двенадцать неизвестных. Для их определения необходима дополнительная информация. Ее можно получить, применив метод пробных грузов, модифицируя и расширяя его возможности введением дополнительной технологической операции. Она состоит в том, что на планшайбу 4 вместо исследуемого тела устанавливается пробный груз с такой же массой, и выполняются те же шесть экспериментов, что и с исследуемым телом. Воспроизводятся те же законы изменения скорости ω₁(φ), ω₂(φ), …, ω₆(φ), для тех же пространственных угловых положений планшайбы 4. Это всегда можно сделать, регулируя систему управления двигателем привода вращения планшайбы, поскольку известны масса груза и его осевые моменты инерции J_Ti. Пробный груз – это цилиндр, собираемый из отдельных дисков с известными инерционными характеристиками.

Затем сообщается ускоренное вращение планшайбе с установленным пробным грузом согласно функции изменения скорости, например, ω₁(φ) на отрезке [φ_m, φ_n]. Определив по экспериментальным данным работу крутящего момента М_1Z(φ) на отрезке [φ_m, φ_n], получим дополнительное уравнение баланса энергий к первому уравнению системы (2)

где (J₁ + J_T1) – известный суммарный момент инерции стенда и пробного груза; $\sum\nolimits_{{{\varphi }_{m}}}^{{{\varphi }_{n}}} {{{M}_{{1rZ}}}(\varphi ,\omega (\varphi ))\Delta \varphi } $ – работа момента сил трения в данном эксперименте на отрезке [φ_m, φ_n].

Полагаем, что моменты сил трения M_rZ(φ, ω(φ)) и M_1rZ(φ, ω(φ)) в опорах качения зависят от веса вращающихся элементов стенда и скорости ω(φ). Поскольку вес пробного груза равен весу исследуемого тела, а скорости на участке движения [φ_m, φ_n] в обоих экспериментах совпадают, полагаем равными и работы моментов сил трения в обоих случаях, т.е.

С учетом равенства (3) получим систему двух уравнений с двумя неизвестными: J_Z и $\sum\nolimits_{{{\varphi }_{m}}}^{{{\varphi }_{n}}} {{{M}_{{rZ}}}(\varphi ,\omega (\varphi ))} \Delta \varphi $

Решение системы относительно J_Z имеет вид

Проведя аналогичные эксперименты для пяти других угловых положений пробного груза, получим значения пяти остальных центральных осевых моментов инерции тела: J_X, J_Y, J_V, J_U, J_W. Например, момент инерции J_U равен

Здесь J_T3 – это момент инерции пробного груза в данном эксперименте.

Из формул (5) и (6) следует, что определяемые моменты инерции тела зависят от моментов инерции пробного груза J_Ti. Однако можно доказать, что количественные значения моментов инерции, найденные по формулам (5) и (6) не зависят от J_Ti.

Действительно, из уравнений системы (4) следует линейное соотношение между работой двигателя, за вычетом потерь энергии на трение, и моментом инерции вращающихся масс (J₁ + J_Z) или (J₁ + J_T1) с коэффициентом пропорциональности λ = = $\frac{{\omega _{1}^{2}({{\varphi }_{n}}) - \omega _{1}^{2}({{\varphi }_{m}})}}{2}$.

Покажем, что изменение момента инерции пробного груза J_T1 на произвольную величину ΔJ, не изменит решения системы уравнений (4) и расчетная величина момента инерции J_Z не изменится.

Уравнение баланса энергий с добавленным моментом инерции ΔJ имеет вид

Преобразуем обе части уравнения (7) следующим образом. Работу момента двигателя $2\sum\nolimits_{{{\varphi }_{m}}}^{{{\varphi }_{n}}} {{{M}_{{2Z}}}} (\varphi )\Delta \varphi $ в правой части (7) можно представить как сумму двух слагаемых. Это работа $2\sum\nolimits_{{{\varphi }_{m}}}^{{{\varphi }_{n}}} {{{M}_{{1Z}}}\left( \varphi \right)} \Delta \varphi $, затраченная на сообщение кинетической энергии массам (J₁ + J_T1) и на работу против сил трения, плюс дополнительная работа ΔA – на сообщение кинетической энергии добавленной массе с моментом инерции ΔJ

Полученное уравнение отличается от второго уравнения системы (4) тем, что к обеим его частям прибавлено одно и то же число $\Delta A = \Delta J(\omega _{1}^{2}({{\varphi }_{n}})$ – $\omega _{1}^{2}({{\varphi }_{m}}))$. Но это эквивалентное преобразование линейного уравнения, не меняющее его корней. Следовательно, полученное новое уравнение совместно с первым уравнением системы (4) имеет те же корни, что и исходная система. Таким образом, изменение момента инерции пробной массы не влияет на величины J_Z и $\sum\nolimits_{{{\varphi }_{m}}}^{{{\varphi }_{n}}} {{{M}_{{rZ}}}(\varphi ,\omega (\varphi ))} \Delta \varphi $.

Из формул (5) и (6) следует также, что собственные инерционные характеристики стенда не влияют на решения (5) и (6) системы (4), поскольку они вообще не входят в расчетные формулы.

Необходимо отметить, что установка дополнительной пробной массы, предусмотренная в методе пробных грузов, меняет динамические характеристики стенда и может быть причиной увеличения погрешности измерений. Но в предлагаемом методе суммарная масса подвижных частей всегда постоянна в процессе выполнения всех экспериментов. Меняются только осевые моменты инерции.

Найденные шесть осевых центральных моментов инерции тела J_X, J_Y, J_Z, J_V, J_U, J_W позволяют по известным формулам рассчитать три центробежных момента инерции [12]

Получены все шесть компонент тензора инерции.

3. Заключение. Разработаны метод и устройство, на котором без переустановки изделия определяются его масса, координаты центра масс и тензор инерции. Переустановка изделия и смена измерительных баз, как известно, источник дополнительных погрешностей.

Единственной измеряемой физической величиной и источником информации для определения инерционных характеристик является время, которое измеряется технологически наиболее просто и точно.

Предложенный метод позволяет расширить номенклатуру исследуемых изделий. Кроме того, упрощается метрологическое обеспечение экспериментов, поскольку фотоэлектрические датчики работают как оптические конечные выключатели.

Установка пробной массы не меняет динамические свойства измерительного стенда и не увеличивает тем самым погрешность получаемых оценок инерционных характеристик. Это отличает предлагаемый метод от уже известных, где приближенно полагается независимость динамических свойств стенда от установки на него дополнительной пробной массы.