Проблемы машиностроения и надежности машин, 2020, № 2, стр. 54-63

ОЦЕНКА НАДЕЖНОСТИ СИСТЕМЫ МОТОР-РЕДУКТОР С ПОМОЩЬЮ МАРКОВСКОЙ МОДЕЛИ

А. И. Абдуллаев¹, И. Г. Чалаби^1, *, **

¹ Азербайджанский технический университет
Баку, Азербайджан

^* E-mail: i_tschalabi@yahoo.de
^** E-mail: i_chalabi@mail.ru

Поступила в редакцию 16.10.2018
После доработки 05.11.2018
Принята к публикации 25.12.2019

DOI: 10.31857/S0235711920020029

Аннотация

В настоящей статье анализируется надежность системы мотор-редуктор при условии, что отказы редуктора при определенных обстоятельствах приводят к выходу из строя двигателя. Состояния системы моделируются цепью Маркова в непрерывном времени. Полученная система дифференциальных уравнений решается с помощью преобразования Лапласа. Таким образом, для различных значений интенсивностей отказов и восстановлений отдельных компонентов можно определить вероятности состояния системы в зависимости от времени, и сравнительно проанализировать коэффициенты готовности.

Ключевые слова: мотор-редуктор, надежность, коэффициент готовности, Марковская модель, преобразование Лапласа

Современные восстанавливаемые приводы машин состоят в основном из различных компонентов и сборочных единиц (механических, электрических, электронных и т.д.), которые отличаются друг от друга по характеру отказов и другим показателям надежности. Таким образом, изменение параметров отказов и восстановлений современных приводов являются случайным процессом. Поэтому анализ надежности приводов можно выполнить с использованием стохастических методов. Передаточная система обычно состоит из компонентов различных производителей (двигатели, муфты, редукторы и т.д.), интенсивности отказов и восстановлений которых приблизительно известны. Если интенсивности отказов и восстановлений отдельных компонентов привода постоянны, то для восстанавливаемой передаточной системы можно применить Марковскую модель. В простейшем случае передаточная система может состоять из независимых восстанавливаемых компонентов. Этот случай часто рассматривался в литературе и успешно решался с помощью Булева–Марковской модели [1–3]. В действительности же отказы компонентов передаточных систем являются в основном зависимыми. Неисправность одного компонента системы может привести к сбою других во время эксплуатации. Поэтому для более точного анализа надежности необходимо учитывать взаимодействие всех компонентов системы. В этом случае Марковская модель может принимать многочисленные состояния для всех мыслимых комбинаций отказов и переходов. Чем больше компонентов имеет передаточная система, тем больше состояний получается, и тем сложнее становятся уравнения состояния. Численное решение системы дифференциальных уравнений возможно с помощью соответствующих компьютерных программ. А аналитическое решение системы дифференциальных уравнений довольно сложно и возможно только при ограниченном числе состояний.

Постановка задачи. Мотор-редукторы широко используются во многих отраслях промышленности благодаря своим положительным характеристикам: компактность, высокий КПД, эффективность и надежность в эксплуатации. Они являются неотъемлемой частью приводов большинства рабочих машин, манипуляторов, производственных цепей и других промышленных оборудований. Поэтому оценка надежности мотор-редукторов имеет большое практическое значение.

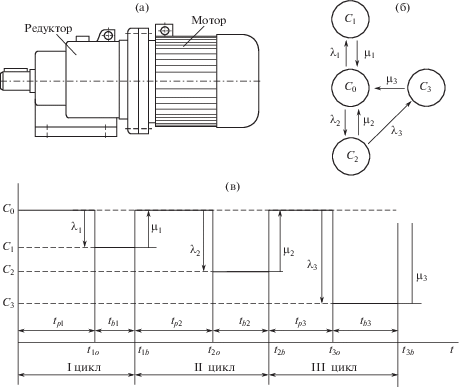
В настоящей статье анализируется надежность сборочной системы, состоящей из двигателя и редуктора (рис. 1a). Принимается во внимание, что отказ редуктора иногда приводит и к сбою двигателя. На практике такой случай происходит часто. Блокировки или вибрации, возникшие из-за отказа (перелом зуба, питтинг, износ и т.д.) зубчатой передачи, также могут впоследствии привести к отказу двигателя. Неисправности системы мотор-редуктор можно разделить на три группы: 1) независимые отказы двигателя. К ним относятся повреждения обмотки, повреждения подшипника двигателя в результате производственных и эксплуатационных сбоев [4, 5]. Статистика показывает, что приблизительно 6% всех отказов мотор-редукторов обусловлены повреждением обмотки [6]; 2) независимые отказы элементов редуктора. Эта группа повреждений включает в себя поломку зуба, питтинг, износ и задирание боковых поверхностей зубов, повреждение вала и повреждение подшипников редуктора. Согласно [6], количество повреждений механических элементов системы мотор-редуктора колеблется между 66 и 90%; 3) зависимые отказы двигателя из-за повреждения редуктора. Иногда сбои в редукторе приводят к сбою двигателя. Например, блокировка редуктора из-за повреждения зуба или повреждения подшипника может привести к перегрузке и нагреву двигателя и последующему разрушению обмотки.

Рис. 1.

Система мотор-редуктор (a), графы состояния (б) и циклы эксплуатации (в) для этой системы.

В простейшем случае, когда интенсивности отказа и восстановления компонентов постоянны, для оценки надежности системы может применяться Марковская модель. Поскольку система мотор-редуктор состоит из двух компонентов, Марковская модель может принимать четыре состояния. Эти состояния и соответствующие им вероятности состояния системы показаны в табл. 1.

Таблица 1.

Описание состояний и вероятности состояния мотор-редуктора

Состояние	Описание	Вероятность состояния
C₀	Оба компонента исправны	P₀(t)
C₁	Двигатель неисправен, редуктор исправен	P₁(t)
C₂	Двигатель исправен, редуктор неисправен	P₂(t)
C₃	Оба компонента неисправны	P₃(t)

На рис. 1б показаны графы состояния системы мотор-редуктор с соответствующими переходами. Интенсивность отказов λ₁ и интенсивность восстановлений μ₁ описывают переходные характеристики двигателя, а интенсивности λ₂ и μ₂ редуктора. Интенсивность отказов λ₃ описывает отказы двигателя вследствие отказов редуктора. Интенсивности отказов λ₁, λ₂ и λ₃ в основном зависят от точности проектирования и условий эксплуатации, а интенсивности восстановлений μ₁, μ₂, μ₃ от структуры и уровня ремонтных работ. Переход от C₀ к C₃ в этой работе не рассматривается, поскольку одновременный сбой обоих компонентов независимо друг от друга происходит очень редко (например, в результате тотальной аварии). Переход от C₁ к C₃ происходит только в исключительных случаях, т.к. двигатель в основном не вызывает отказ зубчатой передачи. Поэтому этот случай здесь тоже не рассматривается.

Процесс эксплуатации рассмотренной системы можно представить как последовательное чередование случайных событий (циклов эксплуатации) интервалов времени работоспособного t_pi и неработоспособного состояний t_bi (рис. 1в). Моменты отказов t_iо (t_1o, t_2o и т.п.) образуют поток событий отказов, а моменты окончания восстановления t_ib (t_1b, t_2b и т.п.) образуют поток событий восстановлений и эти потоки представляют собой стохастические процессы.

Состояния рассматриваемой системы могут моделироваться цепью Маркова в непрерывном времени, принимая допущение, что случайные потоки отказов системы удовлетворяют условиям ординарности и стационарности. В большинстве практических задач данного типа использование Марковской модели приводит к получению решений с погрешностью в пределах допускаемого.

Систему дифференциальных уравнений Колмогорова для рассмотренной системы можно написать согласно [7] и [8] следующим образом

(1)

$\left\{ \begin{gathered} \frac{{d{{P}_{0}}\left( t \right)}}{{dt}} = - \left( {{{{\lambda }}_{1}} + {{{\lambda }}_{2}}} \right){{P}_{0}}\left( t \right) + {{{\mu }}_{1}}{{P}_{1}}\left( t \right) + {{{\mu }}_{2}}{{P}_{2}}\left( t \right) + {{{\mu }}_{3}}{{P}_{3}}\left( t \right), \hfill \\ \frac{{d{{P}_{1}}\left( t \right)}}{{dt}} = {{{\lambda }}_{1}}{{P}_{0}}\left( t \right) - {{{\mu }}_{1}}{{P}_{1}}\left( t \right), \hfill \\ \frac{{d{{P}_{2}}\left( t \right)}}{{dt}} = {{{\lambda }}_{2}}{{P}_{0}}\left( t \right) - ({{{\mu }}_{2}} + {{{\lambda }}_{3}}){{P}_{2}}\left( t \right), \hfill \\ \frac{{d{{P}_{3}}\left( t \right)}}{{dt}} = {{{\lambda }}_{3}}{{P}_{2}}\left( t \right) - {{{\mu }}_{3}}{{P}_{3}}\left( t \right). \hfill \\ \end{gathered} \right.$

Поскольку система мотор-редуктор всегда находится в одном из четырех состояний, сумма всех вероятностей состояния должна быть равным единице для любого момента времени. Соответственно, получаем нормирующее условие

(2)

${{P}_{0}}\left( t \right) + {{P}_{1}}\left( t \right) + {{P}_{2}}\left( t \right) + {{P}_{3}}\left( t \right) = 1.$

В начале работы система в основном находится в работоспособном состоянии, и оба компонента исправны. Таким образом, начальные условия будут

(3)

${{P}_{0}}\left( 0 \right) = 1~\quad {\text{и}}\quad ~{{P}_{i}}\left( 0 \right) = 0\quad {\text{для}}\quad i = 1,~2,~3.$

Для оценки показателей надежности системы мотор-редуктор необходимо определить вероятности состояния системы, решая систему дифференциальных уравнений (1) с учетом нормирующих и начальных условий (2)–(3).

Применение преобразования Лапласа. Как уже упоминалось, систему дифференциальных уравнений (1) можно решить численно. Если число состояний не слишком велико, такие практические проблемы могут быть решены также аналитически, например, с использованием преобразования Лапласа.

Пусть будет ${{\tilde {P}}_{i}}(s)$ преобразование Лапласа для вероятности состояния P_i(t)

$L\left[ {{{P}_{i}}\left( t \right)} \right] = {{\tilde {P}}_{i}}\left( s \right) = \mathop \smallint \limits_0^\infty {{P}_{i}}\left( t \right){{e}^{{ - st}}}dt.$

Используя преобразование Лапласа, и учитывая начальные условия (3), система дифференциальных уравнений (1) принимает вид

(4)

$\left\{ \begin{gathered} s{{{\tilde {P}}}_{0}}\left( s \right) - 1 = - \left( {{{{\lambda }}_{1}} + {{{\lambda }}_{2}}} \right){{{\tilde {P}}}_{0}}\left( s \right) + {{{\mu }}_{1}}{{{\tilde {P}}}_{1}}\left( s \right) + {{{\mu }}_{2}}{{{\tilde {P}}}_{2}}\left( s \right) + {{{\mu }}_{3}}{{{\tilde {P}}}_{3}}\left( s \right), \hfill \\ s{{{\tilde {P}}}_{1}}\left( s \right) = {{{\lambda }}_{1}}{{{\tilde {P}}}_{0}}\left( s \right) - {{{\mu }}_{1}}{{{\tilde {P}}}_{1}}\left( s \right), \hfill \\ s{{{\tilde {P}}}_{2}}\left( s \right) = {{{\lambda }}_{2}}{{{\tilde {P}}}_{0}}\left( s \right) - ({{{\mu }}_{2}} + {{{\lambda }}_{3}}){{{\tilde {P}}}_{2}}\left( s \right), \hfill \\ s{{{\tilde {P}}}_{3}}\left( s \right) = {{{\lambda }}_{3}}{{{\tilde {P}}}_{2}}\left( s \right) - {{{\mu }}_{3}}{{{\tilde {P}}}_{3}}\left( s \right). \hfill \\ \end{gathered} \right.$

Последние три уравнения в (4) позволяют ${{\tilde {P}}_{i}}(s)$ (i = 1, 2, 3) выразить через ${{\tilde {P}}_{o}}(s)$

(5)

$\left\{ \begin{gathered} {{{\tilde {P}}}_{1}}\left( s \right) = \frac{{{{{\lambda }}_{1}}}}{{s + {{{\mu }}_{1}}}}{{{\tilde {P}}}_{0}}\left( s \right), \hfill \\ {{{\tilde {P}}}_{2}}\left( s \right) = \frac{{{{{\lambda }}_{2}}}}{{s + {{{\mu }}_{2}} + {{{\lambda }}_{3}}}}{{{\tilde {P}}}_{0}}\left( s \right), \hfill \\ {{{\tilde {P}}}_{3}}\left( s \right) = \frac{{{{{\lambda }}_{2}}{{{\lambda }}_{3}}}}{{\left( {s + {{{\mu }}_{3}}} \right)\left( {s + {{{\mu }}_{2}} + {{{\lambda }}_{3}}} \right)}}{{{\tilde {P}}}_{0}}\left( s \right). \hfill \\ \end{gathered} \right.$

Учитывая эти выражения в первом уравнении системы (4), получим

${{\tilde {P}}_{0}}\left( s \right)\left[ {s + {{{\lambda }}_{1}} + {{{\lambda }}_{2}} - \frac{{{{{\mu }}_{1}}{{{\lambda }}_{1}}}}{{s + {{{\mu }}_{1}}}} - \frac{{{{{\mu }}_{2}}{{{\lambda }}_{2}}}}{{s + {{{\mu }}_{2}} + {{{\lambda }}_{3}}}} - \frac{{{{{\mu }}_{3}}{{{\lambda }}_{2}}{{{\lambda }}_{3}}}}{{\left( {s + {{{\mu }}_{3}}} \right)\left( {s + {{{\mu }}_{2}} + {{{\lambda }}_{3}}} \right)}}} \right] = 1.$

Или

(6)

${{\tilde {P}}_{0}}\left( s \right)\left[ {\frac{{s({{s}^{3}} + a{{s}^{2}} + bs + c)}}{{\left( {s + {{{\mu }}_{1}}} \right)\left( {s + {{{\mu }}_{3}}} \right)\left( {s + {{{\mu }}_{2}} + {{{\lambda }}_{3}}} \right)}}} \right] = 1,$

здесь

$a = {{{\lambda }}_{1}} + {{{\lambda }}_{2}} + {{{\lambda }}_{3}} + {{{\mu }}_{1}} + {{{\mu }}_{2}} + {{{\mu }}_{3}};$

$b = {{{\lambda }}_{1}}{{{\mu }}_{2}} + {{{\lambda }}_{1}}{{{\lambda }}_{3}} + {{{\lambda }}_{1}}{{{\mu }}_{3}} + {{{\lambda }}_{2}}{{{\lambda }}_{3}} + {{{\lambda }}_{2}}{{{\mu }}_{3}} + {{{\lambda }}_{2}}{{{\mu }}_{1}} + {{{\lambda }}_{3}}{{{\mu }}_{3}} + {{{\lambda }}_{3}}{{{\mu }}_{1}} + {{{\mu }}_{1}}{{{\mu }}_{2}} + {{{\mu }}_{1}}{{{\mu }}_{3}} + {{{\mu }}_{2}}{{{\mu }}_{3}};$

$c = {{{\lambda }}_{1}}{{{\mu }}_{2}}{{{\mu }}_{3}} + {{{\lambda }}_{1}}{{{\lambda }}_{3}}{{{\mu }}_{3}} + {{{\lambda }}_{2}}{{{\lambda }}_{3}}{{{\mu }}_{1}} + {{{\lambda }}_{2}}{{{\mu }}_{1}}{{{\mu }}_{3}} + {{{\lambda }}_{3}}{{{\mu }}_{1}}{{{\mu }}_{3}} + {{{\mu }}_{1}}{{{\mu }}_{2}}{{{\mu }}_{3}}.$

Пусть будут α, β, γ – решения кубического уравнения s³ + as² + bs + c = 0.

Следовательно, получим

(7)

${{s}^{3}} + a{{s}^{2}} + bs + c = \left( {s - {\alpha }} \right)\left( {s - {\beta }} \right)\left( {s - {\gamma }} \right).$

Учитывая условие (7), формулу (6) можно представить в виде

(8)

${{\tilde {P}}_{0}}\left( s \right) = \left[ {\frac{{\left( {s + {{{\mu }}_{1}}} \right)\left( {s + {{{\mu }}_{3}}} \right)\left( {s + {{{\mu }}_{2}} + {{{\lambda }}_{3}}} \right)}}{{s\left( {s - {\alpha }} \right)\left( {s - {\beta }} \right)\left( {s - {\gamma }} \right)}}} \right].$

Для осуществления обратного преобразования формулу (8) можно выражать следующим образом

(9)

${{\tilde {P}}_{0}}\left( s \right) = \frac{M}{s} + \frac{N}{{s - {\alpha }}} + \frac{P}{{s - {\beta }}} + \frac{Q}{{s - {\gamma }}}.$

Параметры M, N, P и Q можно определить сравнением правых частей формул (8) и (9). После преобразований получаем систему уравнений

(10)

$\left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {M + N + P + Q = 1,} \\ { - M\left( { \propto + \;\beta + \gamma } \right) - N\left( {{\beta } + {\gamma }} \right) - P\left( {{\alpha } + {\gamma }} \right) - Q\left( {{\alpha } + {\beta }} \right) = {{{\lambda }}_{3}} + {{{\mu }}_{1}} + {{{\mu }}_{2}} + {{{\mu }}_{3}},} \\ {M\left( {{\alpha \beta } + {\alpha \gamma } + {\beta \gamma }} \right) + N\beta \gamma + P\alpha \gamma + Q\alpha \beta = {{{\mu }}_{1}}{{{\mu }}_{2}} + {{{\mu }}_{2}}{{{\mu }}_{3}} + {{{\mu }}_{1}}{{{\mu }}_{3}} + {{{\mu }}_{1}}{{{\lambda }}_{3}} + {{{\mu }}_{3}}{{{\lambda }}_{3}},} \end{array}} \\ { - M\alpha \beta \gamma = {{{\mu }}_{1}}{{{\mu }}_{2}}{{{\mu }}_{3}} + {{{\mu }}_{1}}{{{\mu }}_{3}}{{{\lambda }}_{3}}.} \end{array}} \right.$

Из последнего уравнения системы (10) можно определить параметр М

$M = - \frac{{{{\lambda }_{3}}{{\mu }_{1}}{{\mu }_{3}} + {{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}}}{{\alpha \beta \gamma }}.$

При известном М, систему уравнений (10) запишем в виде

(11)

$\left\{ {\begin{array}{*{20}{l}} {N + P + Q = 1 - M,} \\ {N\left( {\beta + \gamma } \right) + P\left( {\alpha + \gamma } \right) + Q\left( {\alpha + \beta } \right) = - M\left( {\alpha + \beta + \gamma } \right) - {{\lambda }_{3}} - {{\mu }_{1}} - {{\mu }_{2}} - {{\mu }_{3}},} \\ {N\beta \gamma + P\alpha \gamma + Q\alpha \beta = {{\lambda }_{3}}{{\mu }_{1}} + {{\lambda }_{3}}{{\mu }_{3}} + {{\mu }_{1}}{{\mu }_{2}} + {{\mu }_{1}}{{\mu }_{3}} + {{\mu }_{2}}{{\mu }_{3}} - M\left( {\alpha \beta + \alpha \gamma + \beta \gamma } \right).} \end{array}} \right.~$

C использованием дополнительных параметров n, p и q систему уравнений (11) представим в более простом виде

(12)

$\left\{ {\begin{array}{*{20}{l}} {N + P + Q = n,} \\ {N\left( {{\beta } + {\gamma }} \right) + P\left( {{\alpha } + {\gamma }} \right) + Q\left( {{\alpha } + {\beta }} \right) = p,} \\ {N\beta \gamma + P\alpha \gamma + Q\alpha \beta = q,} \end{array}} \right.~$

где

$n = 1 - M;$

$p = - M\left( {{\alpha } + {\beta } + {\gamma }} \right) - {{{\lambda }}_{3}} - {{{\mu }}_{1}} - {{{\mu }}_{2}} - {{{\mu }}_{3}};$

$q = {{\lambda }_{3}}{{\mu }_{1}} + {{\lambda }_{3}}{{\mu }_{3}} + {{\mu }_{1}}{{\mu }_{2}} + {{\mu }_{1}}{{\mu }_{3}} + {{\mu }_{2}}{{\mu }_{3}} - M\left( {\alpha \beta + \alpha \gamma + \beta \gamma } \right).$

Решая систему уравнений (12) можно определить параметры N, P и Q

$N = \frac{{q + \alpha \left( {n\alpha - p} \right)}}{{\left( {\alpha - \beta } \right)\left( {\alpha - \gamma } \right)}};\quad P = \frac{{\beta \left( {p - n\beta } \right) - q}}{{\left( {\alpha - \beta } \right)\left( {\beta - \gamma } \right)}};\quad Q = \frac{{q + \gamma \left( {n\gamma - p} \right)}}{{\left( {\alpha - \gamma } \right)\left( {\beta - \gamma } \right)}}.$

Теперь применением обратного преобразования в формуле (9) определим вероятности состояния C₀

(13)

${{P}_{0}}\left( t \right) = M + N{{e}^{{\alpha t}}} + P{{e}^{{\beta t}}} + Q{{e}^{{\gamma t}}}.$

Вероятности состояний P₁(t) и P₂(t) можно определить, подставляя формулу (13) в первые два уравнения (5) и применяя последующее обратное преобразование. Для осуществления преобразования Лапласа некоторых элементарных функций использовались формулы из таблицы в [9]. После преобразования получим

(14)

${{P}_{1}}\left( t \right) = \frac{{{{{\lambda }}_{1}}M}}{{{{{\mu }}_{1}}}}(1 - {{e}^{{ - {{{\mu }}_{1}}t}}}) + \frac{{{{{\lambda }}_{1}}N}}{{{{{\mu }}_{1}} + {\alpha }}}({{e}^{{{\alpha }t}}} - {{e}^{{ - {{{\mu }}_{1}}t}}}) + \frac{{{{{\lambda }}_{1}}P}}{{{{{\mu }}_{1}} + {\beta }}}({{e}^{{{\beta }t}}} - {{e}^{{ - {{{\mu }}_{1}}t}}}) + \frac{{{{{\lambda }}_{1}}Q}}{{{{{\mu }}_{1}} + {\gamma }}}({{e}^{{{\gamma }t}}} - {{e}^{{ - {{{\mu }}_{1}}t}}}),$

(15)

$\begin{gathered} {{P}_{2}}\left( t \right) = \frac{{{{{\lambda }}_{2}}M}}{{{{{\lambda }}_{3}} + {{{\mu }}_{2}}}}(1 - {{e}^{{ - \left( {{{{\lambda }}_{3}} + {{{\mu }}_{2}}} \right)t}}}) + \frac{{{{{\lambda }}_{2}}N}}{{{{{\lambda }}_{3}} + {{{\mu }}_{2}} + {\alpha }}}({{e}^{{{\alpha }t}}} - {{e}^{{ - ({{{\lambda }}_{3}} + {{{\mu }}_{2}})t}}}) + \\ + \;\frac{{{{{\lambda }}_{2}}P}}{{{{{\lambda }}_{3}} + {{{\mu }}_{2}} + {\beta }}}({{e}^{{{\beta }t}}} - {{e}^{{ - ({{{\lambda }}_{3}} + {{{\mu }}_{2}})t}}}) + \frac{{{{{\lambda }}_{2}}Q}}{{{{{\lambda }}_{3}} + {{{\mu }}_{2}} + {\gamma }}}({{e}^{{{\gamma }t}}} - {{e}^{{ - ({{{\lambda }}_{3}} + {{{\mu }}_{2}})t}}}). \\ \end{gathered} $

P₃(t) определим из уравнения (2)

(16)

${{P}_{3}}\left( t \right) = 1 - {{P}_{0}}\left( t \right) - {{P}_{1}}\left( t \right) - {{P}_{2}}\left( t \right).$

Определение показателей надежности. Оценка надежности технических систем методами прогнозирования на основе прочностных и трибологических расчетов отдельных ее элементов на стадии проектирования, не всегда отражают реальные значения параметров надежности системы в целом. Более достоверные результаты при оценке надежности могут давать методы, выполняемые на основе статистической обработки результатов испытаний (стендовых, полигонных) и данных эксплуатации. Поэтому для оценки надежности системы мотор-редуктор можно использовать значения интенсивностей отказов λ_i (i = 1, 2, 3) и восстановлений μ_i (i = 1, 2, 3), которые можно определить на основе статистических данных по соответствующим отказам и восстановлениям с помощью выражений

${{\lambda }_{i}} = \frac{{{{n}_{i}}\left( {\Delta t} \right)}}{{N\left( t \right)\Delta t}};\quad {{\mu }_{i}} = \frac{{{{n}_{{bi}}}\left( {\Delta t} \right)}}{{{{N}_{{bi}}}\left( t \right)\Delta t}}~,$

где N(t) – среднее число работоспособных устройств в момент времени t; N_bi(t) – число не восстановленных устройств после соответствующего отказа за промежуток времени Δt; n_i(Δt) – число соответствующих отказов за рассматриваемый промежуток времени Δt; n_bi(Δt) – число восстановленных устройств после соответствующего отказа за промежуток времени Δt.

Одним из основных показателей надежности восстанавливаемых устройств является коэффициент готовности. Поскольку компоненты системы мотор-редуктор обычно соединяются последовательно, коэффициент готовности этой системы можно определить, используя соотношение

$A\left( t \right) = {{P}_{0}}\left( t \right) = M + N{{e}^{{{\alpha }t}}} + P{{e}^{{{\beta }t}}} + Q{{e}^{{{\gamma }t}}}.$

В стационарном процессе вероятности состояния постоянны, а система дифференциальных уравнений становится линейной системой алгебраических уравнений. В этом случае коэффициент готовности можно определить следующим образом

(17)

${{A}_{D}} = \mathop {\lim }\limits_{t \to \infty } {{P}_{0}}\left( t \right) = M = - \frac{{{{\lambda }_{3}}{{\mu }_{1}}{{\mu }_{3}} + {{\mu }_{1}}{{\mu }_{2}}{{\mu }_{3}}}}{{\alpha \beta \gamma }}.$

Вероятности состояний P₁(t), P₂(t) и P₃(t), определяемые по формулам (14), (15) и (16) можно использовать при оценке сроков ремонта и обеспечении запасными частями.

Анализ проведенных вычислений. Формулы (13)–(17) позволяют определить вероятности состояния и коэффициента готовности системы мотор-редуктор для любого момента эксплуатации. Но для этого должны быть известны интенсивности отказов λ₁, λ₂, λ₃ и интенсивности восстановлений μ₁, μ₂, μ₃. Эти параметры можно определять во время эксплуатации на основе статистических данных об отказах и ремонтах. В настоящей статье рассмотрен пример представленной методики для системы мотор-редуктор. Отказы и ремонты подчиняются экспоненциальному закону. Вероятности состояния и коэффициенты готовности были определены для различных значений интенсивностей отказов и восстановлений. Результаты вычислений коэффициента готовности для различных комбинаций параметров (сценариев) представлены в табл. 2.

Таблица 2.

Коэффициент готовности системы для различных сценариев

Параметр–Сценарии	λ₁	λ₂	λ₃	μ₁	μ₂	μ₃	Коэффициент готовности A_D
Сценарий 1	0.2	0.3	1	2	2	1	0.769
Сценарий 2	0.6	1	1	2	2	1	0.509
Сценарий 3	0.2	0.3	1	0.8	1	1	0.647
Сценарий 4	0.2	0.3	2	2	2	1	0.755
Сценарий 5	0.2	0.3	1	2	2	0.5	0.713

Изменения вероятностей состояния для различных сценариев, которые вычислены по формулам (13)–(16) графически представлены на рис. 2–6 . Коэффициент готовности A(t) = P₀(t) при больших t приближается к значению A_D = M (рис. 2–6 ).

Рис. 2.

Вероятность состояния системы мотор-редуктор: сценарий 1: λ₁ = 0.2; λ₂ = 0.3; λ₃ = 1; μ₁ = 2; μ₂ = 2; μ₃ = 1.

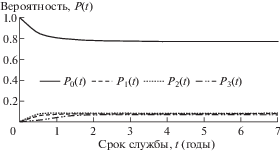
Рис. 3.

Вероятность состояния системы мотор-редуктор: сценарий 2: λ₁ = 0.6; λ₂ = 1; λ₃ = 1; μ₁ = 2; μ₂ = 2; μ₃ = 1.

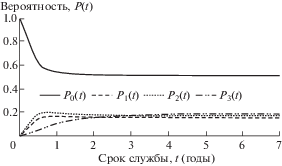
Рис. 4.

Вероятность состояния системы мотор-редуктор: сценарий 3: λ₁ = 0.2; λ₂ = 0.3; λ₃ = 1; μ₁ = 0.8; μ₂ = 1; μ₃ = 1.

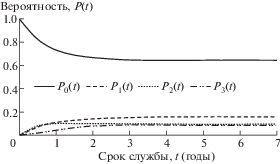
Рис. 5.

Вероятность состояния системы мотор-редуктор: сценарий 4: λ₁ = 0.2; λ₂ = 0.3; λ₃ = 2; μ₁ = 2; μ₂ = 2; μ₃ = 1.

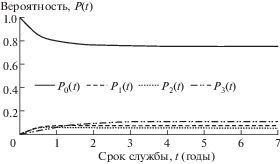
Рис. 6.

Вероятность состояния системы мотор-редуктор: сценарий 5: λ₁ = 0.2; λ₂ = 0.3; λ₃ = 1; μ₁ = 2; μ₂ = 2; μ₃ = 0.5.

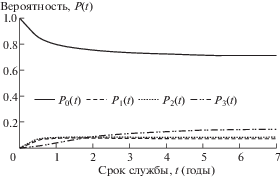
С увеличением независимых интенсивностей отказов λ₁ и λ₂ отдельных компонентов (сценарий 2), снижается коэффициент готовности системы значительно (рис. 3). Вычисления показывают, что при приблизительно трехкратном увеличении интенсивностей отказов λ₁ и λ₂ коэффициент готовности может снижаться на 33.8%. Независимые интенсивности восстановлений отдельных компонентов μ₁ и μ₂ имеют значительное влияние на коэффициент готовности системы. Как видно из рис. 4, снижение значений этих параметров (сценарий 3) приводит к значительному уменьшению коэффициента готовности.

Влияния условной интенсивности отказов λ₃ и соответствующей интенсивности восстановления μ₃, которые возникают в результате отказа другого компонента (рис. 5, 6 ), не являются решающими для коэффициента готовности. Двукратное увеличение интенсивности отказов λ₃ приводит лишь к снижению коэффициента готовности на 1.8% (табл. 2). Расчеты показывают, что при трехкратном увеличении интенсивностей λ₃ коэффициент готовности уменьшается только на 2.9%.

При уменьшении условной интенсивности восстановлений μ₃ (сценарий 5), коэффициент готовности системы снижается не существенно. При двукратном снижении интенсивности восстановлений μ₃, коэффициент готовности уменьшается примерно на 7.3% (табл. 2). Тем не менее, трехкратное снижение интенсивности восстановлений μ₃ может даже привести к 15%-ному уменьшению коэффициента готовности.

Выводы. Надежность и коэффициент готовности системы мотор-редуктор зависят как от совершенства конструкции и условий эксплуатации, так и от структуры и качества ремонтных работ. Вероятности состояния системы мотор-редуктор можно определить аналитически с использованием Марковской модели и преобразования Лапласа в зависимости от времени. Полученные формулы позволяют оценить вероятность безотказной работы мотор-редукторов в процессе эксплуатации в зависимости от интенсивностей отказов и восстановлений отдельных компонентов. Анализ результатов расчетов, представленных в табл. 2 и рис. 2–6, приводит к выводам: 1) независимые интенсивности отказов λ₁, λ₂ и восстановлений μ₁, μ₂ отдельных компонентов оказывают преобладающее влияние на надежность системы мотор-редуктор; 2) влияние условной интенсивности отказа λ₃ и соответствующей интенсивности восстановления μ₃ в результате отказа других компонентов не является решающим для значения коэффициента готовности, но эти параметры также следует учитывать для более точной оценки надежности.

Список литературы

Bertsche B. Reliability in Automotive and Mechanical Engineering. Springer, Berlin, Heidelberg, 2008. 495 p.
Birolini A. Reliability Engineering: theory and practice. Springer, Berlin, Heidelberg, 2004. 593 p.
Гамидов Г.С., Санаев Н.К., Адеев З.И. Системная модель оценки надежности судовых дизелей // Вестник машиностроения. 2009. № 5. С. 25.
Bonfiglioli, Riduttori S.p.A. (Eds.). Gear Motor Handbook. Springer-Verlag, Berlin, Heidelberg, 1995. 606 p.
Ермолин Н.П., Жерихин И.П. Надежность электрических машин. Л.: “Энергия”, 1976. 248 с.
Getriebemotor Kontra Motoranbau über Kupplung. Elektropraktiker, Berlin 54 (2000) 12. S. 10821083
Смирнов Н.В., Дунин-Барковский И.В. Курс теории вероятностей и математической статистики для технических приложений. М.: Наука, 1969. 512 с.
Meyna A., Pauli B. Handbook of Reliability Engineering [in German: Taschenbuch der Zuverlässigkeitstechnik], München: Hanser, 2010. 672 p.
Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. М.: Наука, 1986. 544 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал