Проблемы машиностроения и надежности машин, 2020, № 2, стр. 3-15
ОБЗОР ИССЛЕДОВАНИЙ ПО ИДЕНТИФИКАЦИИ ЛОКАЛЬНЫХ ДЕФЕКТОВ СТЕРЖНЕЙ
А. М. Ахтямов 1, 2, *, М. А. Ильгамов 1, 2, 3
1 Институт механики им. Р.Р. Мавлютова
Уфа, Россия
2 Башкирский государственный университет
Уфа, Россия
3 Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия
* E-mail: AkhtyamovAM@mail.ru
Поступила в редакцию 20.06.2018
Принята к публикации 25.12.2019
Аннотация
В статье дается обзор исследований по трем подходам в решении задач идентификации локальных дефектов стержней и трубопроводов и смежных задач. В первом подходе локальные дефекты моделируются условиями сопряжения, во втором – дельта-функциями, входящими в дифференциальное уравнение, в третьем подходе продольные полости и трещины моделируются непрерывными участками стержня с измененной жесткостью, площадью поперечного сечения и плотностью. В обзоре, состоящем из двух частей, описываются работы, посвященные идентификации дефектов распределенных механических систем с помощью собственных частот, а также с помощью проходящих и отраженных волн. Вторая часть обзора посвящена обзору работ, использующих второй и третий подходы – моделированию дефектов дельта-функциями и непрерывными участками стержня с измененной жесткостью, площадью поперечного сечения и плотностью.
Три основных подхода к обнаружению дефектов в упругих системах. Стержни, балки являются деталями конструкций, в которых могут образовываться локальные дефекты типа трещин, вмятин, полостей, местной коррозии. Важной является задача их ранней диагностики. Часто для выявления дефекта в стержне конечной длины и его местоположения используются собственные частоты колебаний.
В случае стержней большой длины по сравнению с длинами волн такой способ определения дефектов оказывается неудобным. Более подходящим оказывается метод определения дефектов по проходящим и отраженным от них волнам.
Для идентификации дефектов систем с помощью собственных частот, а также с помощью проходящих и отраженных волн будем рассматривать три основных подхода. В первом подходе локальные дефекты моделируются условиями сопряжения, во втором – дельта-функциями, входящими в дифференциальное уравнение. Третий подход применяется, как правило, для протяженных дефектов. В нем продольные полости и трещины моделируются непрерывными участками стержня с измененной жесткостью, площадью поперечного сечения и плотностью.
Существует другой подход, основанный на моделировании дискретной системой жестко закрепленных масс, невесомых пружин или конечно-элементной моделью и описываемой матричным обыкновенным дифференциальным уравнением по времени с постоянными коэффициентами [1, 2]. Такое уравнение имеет конечное число собственных значений, а собственным формам колебаний отвечают собственные векторы. Исследования, выполненные с помощью такого подхода, не являются сложными [3].
В настоящем обзоре описываются работы, посвященные идентификации дефектов распределенных механических систем с помощью собственных частот, а также с помощью проходящих и отраженных волн. Рассматриваются балки, стержни и трубопроводы, которые моделируются непрерывной системой и описываются набором уравнений в частных производных по времени и по одной или нескольким пространственным координатам.
Каждый из подходов имеет свои преимущества и недостатки, о которых более подробно написано в пунктах, посвященных каждому из подходов.
Заметим, что наш обзор связан с интересами авторов и ни в коей мере не претендует на полноту.
Моделирование дефекта условиями сопряжения. Локальные дефекты часто моделируют условиями сопряжения. Для трещин используют условия сопряжения для безмассовых пружин [1], а для полостей – условия для сосредоточенных масс (с отрицательным значением). Первыми, кто показал, что трещины могут быть смоделированы безмассовыми пружинами растяжения-сжатия при продольных колебаниях стержня и вращательной при изгибных колебаниях стержня были Райс и Леви [4]. Связь между глубиной двухсторонней трещины и коэффициентом жесткости пружины установлена в работе [5]. Начиная с работы Фрюнда и Херрмана (Freund, Herrmann) [6], моделирование раскрытой трещины как продольной пружины становится повсеместным, причем не только в теоретических, но и в инженерных исследованиях [7]. Моделировать полость условиями для сосредоточенных масс (или инерционных элементов) впервые было предложено для изгибных колебаний в работе [8], а для продольных – в работе [9].
В последнее время различными авторами предлагаются новые условия сопряжения для трещин. В работе [10] при помощи таких условий сопряжения получены новые результаты об идентификации местоположения и параметров надреза в балке по собственным частотам изгибных колебаний.
В работе [11] для диагностирования надреза предложено использовать собственные частоты из двух спектров изгибных колебаний (вокруг разных осей). Ранее другими авторами использовались два спектра и более спектров [1]. Однако это были спектры задач, которые имели отличающиеся друг от друга краевые условия. А в [11] используются те же самые краевые условия, но рассматриваются колебания вокруг разных осей. Такой подход позволяет доказать корректность обратной задачи и однозначно идентифицировать размеры дефекта (трещины или полости) балки Эйлера–Бернулли. Он позволяет дать “объемное видение” дефекта, подобно тому, как трехмерный объект можно идентифицировать по трем его проекциям. Использование в качестве данных восстановления не только спектров разных задач с дифференциальными уравнениями одного порядка (например, спектров изгибных колебаний вокруг разных осей), но и спектров задач с дифференциальными уравнениями разных порядков (например, спектров изгибных и продольных колебаний стержня) позволяет решать актуальные задачи однозначной идентификации местоположения и размеров дефектов (полостей, надрезов, вмятин и т.п.), решение которых невозможно при использовании традиционных подходов.
Подробно ознакомиться с исследованиями по идентификации местоположения и параметров дефектов можно по двум главам работы [1]. Одна из глав посвящена выявлению дефектов с помощью собственных частот продольных колебаний стержня, другая – идентификации дефектов с помощью собственных частот изгибных колебаний стержня. Мы не будем подробно останавливаться на этих исследованиях. Укажем лишь, что в [12] решена задача нахождения положения s по изменениям двух собственных частот продольных колебаний стержня. В [13] рассматривается задача определения высоты и положения точечной массы, прикрепленной к тонкому стержню по ее воздействию на собственные частоты. В [14] показывается, что положение трещины однозначно определяется по асимтотическому виду спектра. В [16] показано, что жесткость и расположение повреждения однородной свободно опертой балки определяется единственным образом (за исключением симметрии) изменениями m‑й и 2 m-й частот. Альтернативное отождествление задается изменениями m-й частоты балки со свободно опертыми граничными условиями и (m + 1)-й частоты балки с другими краевыми условиями.
Значительное число работ написано авторами, А.Г. Хакимовым, а также А.О. Ватульяном и его учениками.
В [17] по трем собственным частотам изгибных колебаний определяются координата надреза, его глубина и длина. В [18] по двум собственным частотам изгибных колебаний определяются коэффициенты жесткости опор консольной балки. А при известной координате надреза и его длине по собственной частоте определяется его глубина.
В [19] в статической и динамической постановке определяются место и размеры поперечного надреза в вертикальной штанге, растянутой под действием собственного веса и силы, приложенной на нижнем конце. В [20] эта же задача решается с учетом внутреннего трения в пределах надреза. По двум собственным значениям определяется место, соотношение размеров поперечного надреза, а также коэффициент внутреннего трения в пределах надреза в вертикальной штанге, растянутой под действием собственного веса.
В [21, 22] по трем собственным частотам изгибных (крутильных) колебаний балки определяются координата надреза, его глубина и длина.
В [22] по трем собственным частотам крутильных колебаний определены место и размеры повреждения в виде поперечного надреза вала.
В [23–25] по двум собственным частотам изгибных (поперечных) колебаний определяются радиус и толщина утонченной центральной области мембраны.
В [26] по двум собственным частотам крутильных колебаний определены начальная координата и длина продольного сквозного радиального разреза полого вала.
В [27] по трем собственным частотам продольных колебаний определяется начальная координата, величина прикрепленной распределенной массы к ступенчатому стержню и отношение площадей.
В [28] по трем собственным частотам крутильных колебаний определяются координата, длина и параметр надреза бурильной колонны.
В [29] представлено решение задачи идентификации условий замыкания (сопряжения) провода по первым собственным частотам колебаний напряжения в нем; показана корректность задачи; дан метод ее решения и приведены соответствующие примеры.
В [30] приведены результаты расчета местоположения трещины и жесткости в ее области по экспериментальным собственным частотам продольных колебаний.
В [31] показано, что местоположение полости и ее объем определяются по двум собственным частотам изгибных колебаний стержня. Результаты этих исследований хорошо согласуются с результатами работы А.О. Ватульяна, Н.О. Солуянова [32]. Аналогичная модель и выводы приводятся в работах [33, 34], но уже для продольных колебаний стержня.
В [35] предлагается метод, позволяющий вычислить местоположение и объем двух полостей в стержне по собственным частотам изгибных колебаний. В работе [36] полость моделируется условиями сопряжения для сосредоточенных масс (но с отрицательными значениями). В [37] аналогичная задача решена для двух масс, сосредоточенных на балке.
В [38] получены новые результаты об идентификации местоположения и параметров надреза в балке по собственным частотам изгибных колебаний.
Определение местоположения и параметров дефектов с помощью собственных частот удобно для механических распределенных систем конечной длины. Если же объект (например, стержень) оказывается бесконечным, то такой подход оказывается неудобным, т.к. спектр такой задачи является не дискретным, а непрерывным. Более удобным оказывается подход, основанный на использовании проходящих и отраженных волн. Так, например, в [39] рассмотрена задача обнаружения дефектов в протяженных объектах типа штанговых колонн нефтедобывающих скважин и магистральных трубопроводных систем. В таких объектах не все участки могут быть доступны для визуального осмотра и приборного диагностирования [40].
Решение обратной задачи позволяет определить координату надреза и параметр, содержащий его глубину и длину, по данным падающей и отраженной волн в месте наблюдения.
В [41–44] определяется координата надреза и параметр, содержащий его глубину и длину, по данным падающей и отраженной продольной и крутильной волн в месте наблюдения.
В [45] рассматривается отражение от распределенной массы, прикрепленной к трубопроводу, и прохождение изгибной бегущей волны. В этой работе решена обратная задача определения начальной координаты распределенной массы и ее величины по данным отраженной волны в точке наблюдения.
В [46, 47] определяется координата воздушной полости и ее длина по данным отраженной продольной и изгибной волны в месте наблюдения. В [48, 49] определяется начальная координата распределенной массы и ее величина по данным отраженной волны в точке наблюдения.
Изучение продольных и проходящих волн оказывается эффективным не только для протяженных объектов. Оно эффективно и для обнаружения дефектов конечных объектов, подвергшихся ударному воздействию или кратковременному возбуждению. Например, в [50] с помощью проходящих и отраженных волн решается задача определения момента времени удара, длины стержня, массы груза и скорости по данным датчика, который снимает значения смещения стержня в различные моменты времени. Задача решается теоретически с помощью уравнения продольных колебаний однородного стержня. Аналогичные задачи решаются в работах [51, 52].
В [53] получены формулы определения момента и места разрыва трубопровода по данным тензодатчика и предложена схема взаимодействия с ГЛОНАСС, которая позволяет мгновенно обнаруживать места утечек и повреждений трубопроводов, проложенных под водой, и своевременно ликвидировать последствия аварии. В [54] рассматривается обратная ретроспективная задача определения местоположения и момента времени возбуждения струны внешним объектом.
Использование дельта-функций. В предыдущем пункте при изучении колебаний стержней с поперечным надрезом для стыкования решений в двух областях принимается некоторая модель в виде условий сопряжения. Этот подход, приемлемый в случае одного надреза, становится весьма трудоемким при наличии нескольких надрезов в стержне. Кроме того, должна быть задана длина надреза вдоль стержня, между тем она известна не всегда, например, на стадии зарождения трещины. Трудно определима и жесткость пружины в указанной выше модели. Поэтому желательно построить простейшую модель колебаний стержня с несколькими зарождающимися трещинами, в которой отсутствовали бы указанные выше жесткость пружины и длина надреза вдоль стержня (или расстояние между берегами трещины).
Подход, использующий дельта-функции оказывается более эффективным, когда диагностируется не одна, а несколько дефектов. В отечественной литературе, посвященной выявлению дефектов по собственным частотам колебаний, трещины моделируют дельта-функциями в работах Е.И. Шифрина и М.А. Ильгамова. Однако подходы, используемые для моделирования трещин, у этих авторов отличаются.
Поясним сначала подход, используемый Е.И. Шифриным на примере продольных колебаний стержня. Он получает уравнения с дельта-функциями основываясь на условиях сопряжения для трещин. В работах [55, 56] вместо функции u(x), характеризующей продольные смещения при продольных колебаниях стержня, используется функция, которая является решением уравнений Штурма–Лиувилля
Вводится гладкая функция
Продифференцировав это уравнение и введя новую переменную
получается уравнениеВ [60] рассмотрена задача, аналогичная задаче [56], но для стержня переменного сечения. Предполагается, что площадь сечения является непрерывно дифференцируемой функцией координаты. Получены результаты, аналогичные результатам [56], т.е. путем сведения задачи к обратной задаче Штурма–Лиувилля доказано, что любое число трещин однозначно идентифицируется по двум спектрам, отвечающим условиям свободный – свободный и свободный закрепленный на концах. Рассмотрены численные примеры.
В работе [61] рассмотрены задачи идентификации конечного числа малых трещин в стержне и балке по собственным частотам. Малым трещинам отвечают пружины с малыми податливостями. Это позволяет упростить задачу и свести ее к линейным относительным податливостям пружин. Задачу о продольных колебаниях стержня со свободными концами удается свести к уравнениям, встречающимся в различных областях чистой и прикладной математики (в задачах анализа сигналов, идентификации простых полюсов мероморфной функции, реконструкции полигональной области по комплексным моментам, идентификации малых дефектов в упругих телах и др.). Методы решения таких уравнений хорошо известны. Получены следующие результаты. Если известно, что в стержне имеется не более чем N трещин, то с помощью 2N собственных частот, отвечающих продольным колебаниям стержня со свободными концами, можно определить пары точек, расположенных симметрично относительно середины стержня, в которых могут находиться трещины, и суммарную податливость стержней, расположенных в симметричных точках. Кроме этого, показано, что с помощью 2N + 1 собственных частот, отвечающих продольным колебаниям стержня, один конец которого закреплен, а другой свободен, можно определить пары точек, расположенных симметрично относительно середины стержня, в которых могут находиться трещины, и разность податливостей пружин, расположенных в симметричных точках. Рассмотрена также задача о поперечных колебаниях свободно опертой балки с малыми трещинами. В этой задаче получены результаты, аналогичные результатам для продольных колебаний стержня со свободными концами. Более точно, для случая, когда известно, что в балке находится не более N трещин, разработан алгоритм, позволяющий по 2N собственным частотам определить пары симметричных точек возможного расположения трещин и суммарную податливость пружин, работающих на поворот.
Другой подход к моделированию трещин дельта-функциями используется в работах М.А. Ильгамова. В нем учитывается особенность зарождающейся трещины, состоящая в том, что в фазе деформации сжатия она исчезает (смыкание берегов трещины), а в фазе деформации растяжения эти берега расходятся. В работе [62] предполагается, что при продольных колебаниях стержня в фазе деформации сжатия берега трещины приходят в соприкосновение, в результате чего движение не отличается от случая сплошного стержня (без трещины). В фазе деформации растяжения эти берега расходятся, в результате чего происходит частичное прохождение продольной волны и ее частичное отражение. Так же, как при моделировании трещины условиями сопряжения, не учитывается пространственное напряженно-деформированное состояние в зоне трещины. Оно предполагается одноосным. Последнее, естественно, не отражает истинную картину напряженно-деформированного состояния вблизи трещины, но может служить некоторым приближением при определении интегральных характеристик как собственные частоты продольных колебаний всего стержня. Указанное отражение волн от трещины в фазе растяжения приводит к взаимодействию разных гармоник продольных колебаний стержня конечной длины, что сильно усложняет анализ. Если принять отношение суммы площадей Fk трещин числом K к общей площади F поперечного сечения балки (рис. 1) порядка 0.1, то взаимодействие гармоник будет не сильным и собственные формы будут мало отличаться от соответствующих форм колебаний стержня без трещин. В [62] рассматривается именно случай $\sum\nolimits_{k = 1}^K {\left( {{{{{F}_{k}}} \mathord{\left/ {\vphantom {{{{F}_{k}}} F}} \right. \kern-0em} F}} \right)} \ll 1$. Это простейшее качественное решение может быть уточнено при учете взаимодействия гармоник.
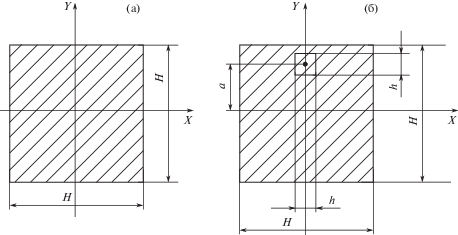
Рис. 1.
Поперечные сечения рассматриваемых стержней: (а) сплошной стержень, форма сечения – квадрат; (б) трубчатый стержень, форма сечения – квадрат с полостью.
В уравнении продольного движения стержня ${{\partial N} \mathord{\left/ {\vphantom {{\partial N} {\partial x}}} \right. \kern-0em} {\partial x}}$ – $\rho F{{{{\partial }^{2}}u} \mathord{\left/ {\vphantom {{{{\partial }^{2}}u} {\partial {{t}^{2}}}}} \right. \kern-0em} {\partial {{t}^{2}}}} = 0$ усилие N принимается в виде N = $E\left( {F\frac{{\partial u}}{{\partial x}} - \sum\nolimits_k {{{F}_{k}}L\delta \left( {x - {{x}_{k}}} \right)\frac{{\partial u}}{{\partial x}}} } \right)$, где Е, ρ – модуль упругости и плотность материала; и – перемещение, δ(x – xk) – дельта-функция; xk – координата k-й трещины. Трещины могут быть расположены по длине L стержня произвольно. Из последних двух уравнений следует
Для описания деформации сжатия второй член в последнем уравнении следует опустить (в отсутствии трещины fk = 0).
Условия на концах стержня принимаются в виде
Этим условиям на концах стержня и условиям стыкования решений удовлетворяют функции для обеих фаз деформации
Чем больше число зарождающихся трещин и чем более равномерно они расположены по длине стержня, тем одночленная аппроксимация перемещения точнее отражает картину деформации (в общем случае необходимо брать суммы по i).
С применением этой приближенной модели в [62] определяются собственные частоты, значения которых сравниваются с результатами другой модели, учитывающей не только площадь, но и продольный размер трещины. Показано, что при отношении длины трещины к общей длине стержня, имеющем порядок отношения площади трещины к площади поперечного сечения стержня, можно не учитывать размер трещины вдоль стержня.
Моделирование дефекта непрерывным участком стержня с измененной жесткостью, площадью поперечного сечения и плотностью. Моделирование непрерывными участками стержня с измененной жесткостью, площадью поперечного сечения и плотностью, как правило, применяется при идентификации протяженных дефектов. Часто при решении задачи используются аналитические методы решения. Поэтому такой подход удобен для ответа на фундаментальные вопросы. Например, с помощью такого подхода может быть получен важный для дефектоскопии вопрос: Всегда ли по собственным частотам свободных изгибных колебаний стержня можно выявить дефект?
Как показывают исследования, проведенные в работах [8, 63, 64] собственные частоты поперечных колебаний балки с полостью на срединной оси выше собственных частот колебаний сплошной балки. Это в корне отличается от поведения частот колебаний балки с открытой трещиной. Собственные частоты балки с раскрытой трещиной ниже собственных частот сплошной бездефектной балки [65].
При перемещении полости балки от срединной оси к внешнему краю, балка с полостью становится в итоге балкой с открытой трещиной. На основе этого факта, а также учитывая сведения о том, что собственные частоты балки с полостью выше, а балки с трещиной, наоборот, ниже собственных частот сплошной бездефектной балки, сделаем предположение: при определенном положении полости балки, собственные частоты колебаний балки с полостью совпадают с собственными частотами колебаний сплошной бездефектной балки.
В работе [66] показана справедливость данного предположения на примере изгибных колебаний сплошного бездефектного стержня и стержня с призматической полостью, проходящей по всей длине стержня (трубчатого стержня) (рис. 1).
Задача об изгибных колебаниях консольной балки длины $L$ заменой $u\left( {x,t} \right)$ = $y\left( x \right)\cos \omega t$ сводится к спектральной задаче
(1)
$\begin{gathered} {{y}^{{(4)}}}\left( x \right) = {{\lambda }^{4}}y(x), \\ y(0) = 0,\quad y{\kern 1pt} {\kern 1pt} '(0) = 0,\quad y{\kern 1pt} ''(L) = 0,\quad y{\kern 1pt} '''(L) = 0, \\ \end{gathered} $Как видно из рис. 1, параметр $a$ определяет положение полости трубчатого стержня. При $a = 0$ полость лежит на срединной оси стержня. При значениях параметра $a \geqslant \left( {\frac{H}{2} - \frac{h}{2}} \right)$ рассматриваемый трубчатый стержень превращается в стержень с открытой трещиной. Как было отмечено ранее, собственные частоты стержня с полостью на срединной оси выше, а стержня с трещиной, наоборот, ниже собственных частот сплошного стержня. Следовательно, при определенных значениях параметра $a$ собственные частоты трубчатого стержня совпадают с собственными частотами сплошного стержня. Необходимо выяснить при каких значениях параметра $a$ происходит совпадение частот.
В терминах задачи (1), (2) данная задача сводится к исследованию того, при каких значениях параметра $a$ выполняется соотношение $\frac{{{{J}_{1}}}}{{{{F}_{1}}}} = \frac{{{{J}_{2}}}}{{{{F}_{2}}}}$, где ${{J}_{1}}$, ${{F}_{1}}$ – момент инерции и площадь поперечного сечения сплошного стержня, ${{J}_{2}}$, ${{F}_{2}}$ – момент инерции и площадь поперечного сечения трубчатого стержня. В работе [66] показано, что при
Таким образом, выявить дефект по спектру частот колебаний стержня вокруг одной оси оказывается невозможным. В [66, 67] показано, что для идентификации полости необходимо использование собственных частот из двух спектров изгибных колебаний (вокруг разных осей). По двум собственным частотам, каждая из которых взята из спектров частот изгибных колебаний стержня с полостью вокруг разных осей, можно однозначно идентифицировать параметры размера h и местоположения a полости.
Третий подход позволяет также решать задачи идентификации дефектов. Так, в [68] исследованы собственные изгибные колебания трубопровода с движущейся жидкостью, находящегося под действием растягивающей силы и защемленного по краям. По трем частотам изгибных колебаний находятся скоростной параметр, относительная масса продукта на единицу длины трубопровода и относительная масса отложений на стенках трубопровода.
В [69] исследуются собственные крутильные колебания трехэлементного вала. По четырем частотам свободных крутильных колебаний можно определить параметр жесткости, полярный момент инерции вала на втором участке, начальную координату и длину этого участка.
В [70] решена задача о поиске местонахождения границы между двумя участками стержня разной плотности по собственным частотам его свободных продольных колебаний.
В [71] сформулирована математическая модель неоднородного стержня с коррозионным участком. Решена задача определения длины, модуля упругости и плотности коррозионного участка стрежня по трем собственным частотам продольных колебаний.
В [72] рассмотрена балка с поперечным сечением в виде полого прямоугольника. Определяются размеры полости балки по двум собственным частотам изгибных колебаний, взятым из разных спектров. Данные спектры принадлежат колебаниям в двух взаимно перпендикулярных плоскостях.
В [73] исследовано поведение собственных частот балки с продольным надрезом (трещиной). Для идентификации глубины и ширины предложено использование двух спектров частот (вокруг разных осей). Показано как по двум собственным частотам, взятым из разных спектров (вокруг разных осей), идентифицировать глубину и ширину надреза балки.
В [74] получены формулы идентификации размеров призматического стержня по трем собственным частотам (по одной из спектра продольных колебаний и из двух спектров изгибных колебаний вокруг разных осей). Найдены аналогичные формулы для стержней треугольного и эллипсовидного сечений.
Значительный вклад в вопросы идентификации дефектов, моделируемых участками с иной плотностью или жесткостью, внесен научной школой А.О. Ватульяна. В работах этой научной школы полости, сначала участки с другой плотностью или жесткостью рассматриваются как участки определенной формы, а затем предлагаются подходы, позволяющие рассматривать участки произвольной формы.
В [63] предложен подход к определению расположения и объема полости произвольной формы. Представлены результаты численных экспериментов и их анализ.
В [75] приведены схемы реконструкции полости в стержне при анализе продольных и изгибных колебаний стержня.
В [76] дан обзор работ по обратным задачам теории трещин в упругих телах. Отмечено, что наиболее популярным является модель, в которой трещина моделируется математическим разрезом, а берега не взаимодействуют в процессе установившихся колебаний.
В [77] представлен метод определения параметров малой осесимметричной полости в балке при анализе продольных и изгибных колебаний. Наиболее просто реализуется предложенная схема для сферической полости в цилиндрическом стержне. Представлены вычислительные эксперименты по реконструкции параметров полости и его положения.
В [32] рассматривается задача об установившихся поперечных колебаниях цилиндрического стержня, содержащего осесимметричный дефект в форме полости малого характерного размера. Представлены численные результаты, показавшие достаточную эффективность предлагаемого в статье похода по восстановлению объема и центра полости.
В [78] рассматриваются задачи о восстановлении переменных модуля упругости и плотности для упругого неоднородного стержня при возбуждении продольных и изгибных колебаний.
В [79] исследованы поперечные колебания консольно закрепленной балки с тонким надрезом, который смоделирован как локальное изменение жесткости. Разработаны методы поэтапной реконструкции параметров надреза по известной информации о резонансных частотах балки с надрезом или об амлитудно-частотной характеристике торца.
В [80] представлен метод определения параметров симметричного тонкого надреза в балке при анализе изгибных колебаний. Реализована процедура поэтапного восстановления параметров тонкого надреза.
В [81] решены две обратные задачи. Первая состоит в определении центра и объема эллипсоидального включения, ослабляющего упругий стержень, при известных его физических характеристиках (модуль Юнга и плотность), а вторая – в определении физических параметров включения при известной его геометрии. В обеих задачах входной информацией являются значения первых трех или четырех резонансных частот.
Список литературы
Gladwell G.M.L. Inverse Problems in Vibration. 2nd ed. Dordrecht, Boston, London: Kluwer Academic Publishers, 2004. (Русский перевод: Гладвелл Г.М.Л. Обратные задачи теории колебаний. М. Ижевск: НИЦ Регулярная и хаотическая динамика, Институт компьютерных исследований, 2008).
Chu M.T., Golub G.H. Inverse Eigenvalue Problems: Theory, Algorithms, and Applications. Oxford University Press, USA, 2005. 406 p.
Ахтямов А.М. Диагностирование нагружености механической системы // Приборы и системы. Управление, контроль, диагностика. 2003. № 6. С. 60.
Rice J.R., Levy N. The part through surface crack in an elastic plate // J. Appl. Mech. 1972. V. 39. P. 185.
Ruotolo R., Surace C. Natural frequencies of a bar with multiple cracks // Journal of sound and vibrations. 2004. V. 272. P. 301.
Freund L.B., Herrmann G. Dynamic fracture of a beam or plate in plane bending // Journal of applied mechanics. 1976. V. 76. P. 112.
Cawley P., Adams R.D. The location of defects in structures from measurements of natural frequencies // Journal of strain anaysis. 1979. V. 14. P. 49.
Ахтямов А.М., Аюпова А.Р. Диагностирование полости в стержне методом отрицательной массы // Дефектоскопия. 2010. Т. 46. № 5. С. 29.
Ахтямов А.М., Сатыев Э.И. Определение местоположения и объема полости в упругом стержне по двум собственным частотам его колебаний // Дефектоскопия. 2012. № 5. С. 78.
Ватульян А.О., Осипов А.В. Поперечные колебания балки с локализованными неоднородностями // Вестник ДГТУ. 2012. № 8 (69). С. 34.
Ахтямов А.М., Ильгамов М.А. Модель изгиба балки с надрезом: прямая и обратная задачи // Прикладная механика и техническая физика. 2013. Т. 54. № 1. С. 152.
Morassi A. Identification of a crack in a rod based on changes in a pair of natural frequencies // Journal of sound and vibration. 2001. V. 242. P. 577.
Morassi A., Dilena M. On point mass identification in rods and beams from minimal frequency measurements // Inverse problems in engineering. 2002. V. 10. P. 183.
Morassi A. An uniqueness result on crack localization in vibrating rods // Inverse problems in engineering. 1997. V. 4. P. 231.
Hald O.H. Discontinuous inverse eigenvalue problems // Communications on pure and applied mathematics. 1984. V. 37. P. 539.
Morassi A. The crack detection problem in vibrating beams, in Davini C. and Viola E. (Eds) Problems in Structural Identification and Diagnostics: General Aspects and Applications. New York: Springer, 2003. P. 163.
Ильгамов М.А., Хакимов А.Г. Диагностика повреждений консольной балки с надрезом // Дефектоскопия. 2009. № 6. С. 83.
Ильгамов М.А., Хакимов А.Г. Диагностика закрепления и повреждений балки на упругих опорах // Контроль. Диагностика. 2010. № 9. С. 57.
Ильгамов М.А. Диагностика повреждений вертикальной штанги // Труды Института механики Уфимского научного центра РАН. Вып. 5. Уфа: Гилем, 2007. С. 201.
Ахметвалиева Э.Н., Ахтямов А.М. Диагностика поперечного надреза вертикальной штанги // Контроль и диагностика. 2012. № 8. С. 31.
Ильгамов М.А., Хакимов А.Г. Диагностика повреждений балки на шарнирных опорах // Строительная механика инженерных конструкций и сооружений. 2010. № 2. С. 42.
Хакимов А.Г. О собственных колебаниях вала с моделью искусственного дефекта // Дефектоскопия. 2010. № 6. С. 93.
Хакимов А.Г. О собственных колебаниях круглой плиты с утонченной центральной областью // Строительная механика инженерных конструкций и сооружений. 2011. № 3. С. 63.
Хакимов А.Г. О собственных колебаниях круглой плиты с утонченной центральной областью и прикрепленной распределенной массой // Строительная механика инженерных конструкций и сооружений. 2015. № 4. С. 38.
Хакимов А.Г. О собственных колебаниях круглой мембраны с утонченной центральной областью // Контроль. Диагностика. 2011. № 4. С. 66.
Хакимов А.Г. О собственных крутильных колебаниях полого вала с продольным сквозным радиальным разрезом // Дефектоскопия. 2013. № 6. С. 32.
Хакимов А.Г. О собственных продольных колебаниях ступенчатого стержня с распределенной присоединенной массой // Контроль. Диагностика. 2013. № 11. С. 9.
Хакимов А.Г., Сатыев Э.И. О собственных крутильных колебаниях бурильной колонны // Электронный научный журнал Нефтегазовое дело. 2014. № 6. С. 120.
Ахтямов А.М., Ямилова Л.С. Идентификация условий замыкания провода по собственным частотам колебаний напряжения переменного тока // Электромагнитные волны и электронные системы. 2006. Т. 11. № 2–3. С. 15.
Ахтямов А.М., Каримов А.Р. Идентификация трещины в стержне по двум собственным частотам продольных колебаний // В мире научных открытий. 2012. № 1. С. 111.
Ахтямов А.М., Аюпова А.Р. Определение полости в стержне методом отрицательной массы // Дефектоскопия, 2010. № 5. С. 29.
Ватульян А.О., Солуянов Н.О. Идентификация полости в упругом стержне при анализе поперечных колебаний // ПМТФ. 2008. № 6. Т. 49. С. 152.
Ахтямов А.М., Сатыев Э.И. Определение местоположения и объема полости в упругом стержне по двум собственным частотам его колебаний // Дефектоскопия. 2012. № 5. С. 78.
Ахтямов А.М., Сатыев Э.И. Диагностика повреждения вертикальной штанги с учетом внутреннего трения // Контроль. Диагностика. 2013. № 6. С. 35.
Ахтямов А.М., Аюпова А.Р. О решении задачи диагностирования дефектов в виде малой полости в стержне // Журнал Средневолжского математического общества. 2010. Т. 12. № 3. С. 38.
Ахтямов А.М., Аюпова А.Р. Определение полости в стержне методом отрицательной массы // Дефектоскопия. 2010. № 5. С. 29.
Ахтямов А.М., Аюпова А.Р. Диагностирование двух масс, сосредоточенных на балке // Приборы и системы. Управление, контроль, диагностика. 2010. № 1. С. 42.
Ватульян А.О., Осипов А.В. Поперечные колебания балки с локализованными неоднородностями // Вестник ДГТУ. 2012. № 8 (69). С. 34.
Ильгамов М.А., Хакимов А.Г. Отражение затухающей бегущей волны от надреза в стержне // Известия Российской академии наук. Механика твердого тела. 2011. № 4. С. 116.
Сидоров Б.В., Мартынов С.А. Рекомендуемая технология диагностики подземных трубопроводов // Контроль. Диагностика. 2005. № 12. С. 18.
Ильгамов М.А., Хакимов А.Г. Отражение продольной волны от надреза в стержне, погруженном в вязкую жидкость // Вычислительная механика сплошных сред. 2010. Т. 3. № 3. С. 58.
Ильгамов М.А., Хакимов А.Г. Отражение продольной бегущей волны в стержне с повреждением // Контроль. Диагностика. 2009. № 7. С. 43.
Ильгамов М.А., Хакимов А.Г. Отражение продольной бегущей волны от надреза в стержне // Техническая акустика. 2008. Т. 8. С. 16.
Хакимов А.Г. Отражение крутильной бегущей волны в стержне с искусственным дефектом // Вычислительная механика сплошных сред. 2012. Т. 5. № 1. С. 114.
Хакимов А.Г. Отражение изгибной волны от распределенной массы, прикрепленной к трубопроводу // Математическое моделирование. 2013. Т. 25. № 6. С. 80.
Ильгамов М.А., Хакимов А.Г. Отражение продольной волны от воздушной полости в трубопроводе // Известия Уфимского научного центра РАН. 2012. № 4. С. 15.
Хакимов А.Г. Отражение длинной изгибной бегущей волны от точечной воздушной полости в трубопроводе // Контроль. Диагностика. 2012. № 4. С. 58.
Хакимов А.Г. Отражение изгибной волны от распределенной массы, прикрепленной к трубопроводу // Математическое моделирование. 2013. Т. 25. № 6. С. 80.
Хакимов А.Г. Отражение короткой изгибной бегущей волны от распределенной массы, прикрепленной к трубопроводу // Труды Института механики им. Р.Р. Мавлютова УНЦ РАН. 2012. Т. 9. № 2. С. 134.
Ахтямов А.М. Определение массы, скорости движения груза и места его удара по стержню с помощью продольных смещений одного из сечений стержня // Контроль. Диагностика. 2007. № 11. С. 59.
Ахтямов А.М., Муртазина Р.Ф. Определение массы, скорости движения груза и места его удара по стержню с помощью показаний тензодатчика // Контроль. Диагностика. 2009. № 1. С. 36.
Утяшев И.М., Ахтямов А.М. Идентификация повреждения трубопровода с использованием тензодатчиков // Труды Института механики им. Р.Р. Мавлютова УНЦ РАН. 2012. Т. 9. № 2. С. 130.
Утяшев И.М., Ахтямов А.М. Идентификация повреждения трубопровода с использованием тензодатчиков // Труды Института механики им. Р.Р. Мавлютова УНЦ РАН. 2012. Т. 9. № 2. С. 130.
Ахтямов А.М., Утяшев И.М. Ретроспективная задача распространения поперечных волн // Контроль. Диагностика. 2010. № 4. С. 36.
Shifrin E.I., Ruotolo R. Natural frequencies of a beam with an arbitrary number of cracks // Journal of Sound and Vibration. 1999. V. 222. № 3. P. 409.
Shifrin E.I. Inverse spectral problem for a rod with multiple cracks // Mechanical Systems and Signal Processing. 2015. V. 56–57. P. 181.
Крейн М.Г. Об обратных задачах для неоднородной струны // ДАН СССР. 1952. Т. 82. С. 669.
Крейн М.Г. Об одном обобщении исследований Стилтьеса // ДАН СССР. 1952. Т. 87. С. 881.
Крейн М.Г. О некоторых случаях эффективного определения плотности неоднородной струны по ее спектральной функции // ДАН СССР. 1953. Т. 93. С. 617.
Shifrin E.I. Inverse spectral problem for a non-uniform rod with multiple cracks // Mechanical Systems and Signal Processing. 2017. V. 96. P. 348.
Shifrin E.I. Identification of a finite number of small cracks in a rod using natural frequencies // Mechanical Systems and Signal Processing. 2016. V. 70–71. P. 613.
Ильгамов М.А. Продольные колебания стержня с зарождающимися поперечными трещинами // МТТ. 2017. № 1. С. 23.
Ватульян А.О., Солуянов Н.О. Об определении местоположения и размера полости в упругом стержне // Дефектоскопия. 2005. № 9. С. 44.
Ахтямов А.М., Каримов А.Р. Диагностирование полости в призматической балке // Дефектоскопия. 2013. № 3. С. 15.
Morassi A. Crack-induced changes in eigenparameters on beam structures // Journal of engineering mathematics. V. 119. P. 1798.
Ахтямов А.М., Саляхова Е.В. Всегда ли наличие полости в стержне меняет собственные частоты? // Электронный журнал “Техническая акустика”, http://ejta.org, 2011. 7.
Ахтямов А.М., Саляхова Е.В. Диагностирование полости в стержне // Журнал Средневолжского математического общества. № 2. Т. 13. С. 47.
Хакимов А.Г. Определение массового расхода жидкости в трубопроводе и толщины отложений на его стенках по собственным частотам изгибных колебаний // Известия Уфимского научного центра РАН. 2016. № 3. С. 15.
Хакимов А.Г. К определению параметров трехэлементного вала по заданному спектру частот крутильных колебаний // Контроль. Диагностика. 2014. № 6. С. 29.
Ахтямов А.М., Галеева Д.Р. Исследование прямой и обратной задачи о колебаниях неоднородного стержня, состоящего из двух различных участков // Контроль. Диагностика. 2014. № 4. С. 58.
Ахтямов А.М., Галеева Д.Р. Определение длины, плотности и модуля упругости коррозионного участка стержня по собственным частотам продольных колебаний // Вестник Башкирского университета. 2015. Т. 20. № 2. С. 398.
Ахтямов А.М., Каримов А.Р. Диагностирование полости в призматической балке // Дефектоскопия. 2013. № 3. С. 15.
Ахтямов А.М. Идентификация продольного надреза балки по ее собственным частотам // Вестник Башкирского университета. 2012. Т. 17. № 2. С. 840.
Ахтямов А.М. Диагностирование размеров стержня по его собственным частотам // Приборы и системы. Управление, контроль, диагностика. 2011. № 11. С. 51.
Ватульян А.О. О колебаниях упругих тел с малыми дефектами // Известия вузов, Сев.-Кавк. рег. 2004. Спецвыпуск. С. 19.
Ватульян А.О., Соловьев А.Н. Обратные задачи теории трещин в твердых телах// Известия вузов, Сев.-Кавк. рег. 2004. Спецвыпуск “Математика и механика сплошной среды”. С. 74.
Ватульян А.О., Бочарова О.В., Жарков Р.С. Реконструкция малых полостей в упругих стержнях // Изв вузов. Сев.-Кавк. рег. Сер. естеств. науки. 2006. № 2. С. 28.
Ватульян А.О., Бочарова О.В. О реконструкции плотности и модуля Юнга для неоднородного стержня // Акустический журнал. 2009. Т. 55. № 3. С. 275.
Ватульян А.О., Осипов А.В. Об определении характеристик тонкого надреза при анализе изгибных колебаний балки // Экологический вестник ЧЭС. 2013. № 2. С. 27.
Ватульян А. О., Осипов А.В. Об одном подходе при определении параметров дефекта в балке // Дефектоскопия. 2014. № 11. С. 37.
Ватульян А.О., Каштальян Д.О. Об определении зоны деструкции в упругой балке // Изв. вузов. Северо-Кавказский регион. Сер. естеств. науки. 2015. № 4. С. 29.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин


