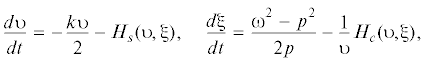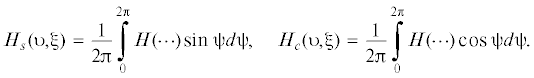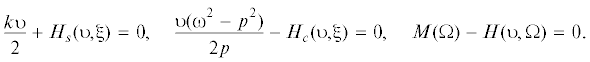Проблемы машиностроения и надежности машин, 2020, № 2, стр. 25-30

1. Систематическая теория колебательных систем с ограниченным возбуждением или источниками энергии ограниченной мощности была создана В.О. Кононенко и изложена в его основополагающей монографии [1, 2]. Эта теория была развита в дальнейшем его последователями ([3–5] и др.). Особую актуальность она приобрела в связи с проблемами экологии. Связь проблем экологии с потребляемой энергией, метрологией, точностью моделей расчета систем, точностью обработки, колебаниями отмечена в работе [6].

В радиотехнике, устройствах автоматического управления, электронике и др. широко распространены системы с запаздыванием. Наличие запаздывания имеет двоякое значение: быть полезным (запаздывание вводится специально, например, на ультразвуковых станках) или вредным. В следящих системах, прокатных станах, регуляторах, вибрационных машинах и др. возникают колебания, обусловленные запаздыванием. Запаздывание в механических системах обуславливается характеристикой внутреннего трения в материалах, несовершенством их упругих свойств (наличие гистерезиса статической характеристики и упругое последействие) и др. [“Энциклопедия по машиностроению”]. Задачи с запаздыванием без учета взаимодействия колебательной системы и источника энергии рассматривались в большом числе работ ([7–10] и др.), а задачам с учетом этого взаимодействия посвящено мало работ.

Для анализа нелинейных колебательных систем существует ряд приближенных методов: усреднения, энергетического баланса, гармонической линеаризации ([8, 12, 13] и др.). Использование этих методов сопряжено большими затратами труда, времени и др. Эти недостатки значительно снижаются в случае применения методов прямой линеаризации нелинейностей, описанных в работах ([6, 14–16] и др.). Такое преимущество методов прямой линеаризации, наряду с простотой их применения, особенно важно при создании реальных технических устройств. Целью работы является развитие на основе методов прямой линеаризации процедуры расчета смешанных колебаний в системах с ограниченным возбуждением. При наличии запаздывания и ограниченной мощности источника энергии в нелинейной системе можно использовать описанную процедуру применения методов прямой линеаризации. Эта процедура достаточно простая, что особенно важно с практической точки зрения – для расчета параметров механизмов, машин, оборудования на стадии их проектирования.

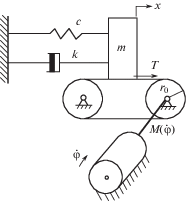
2. Рассмотрим известную модель (рис. 1) автоколебательной системы [1, 3, 17, 18]. С учетом запаздывающей упругой силы движение системы описывается уравнениями

где ${\lambda }\sin {\nu }{\kern 1pt} t$ – внешняя сила с постоянной амплитудой и частотой; $T(U)$ – нелинейная сила трения, зависящая от относительной скорости $U = V - \dot {x}$, $V = {{r}_{0}}{\kern 1pt} \dot {\varphi }$ и вызывающая автоколебания; ${{r}_{0}} = {\text{const}}$ – радиус точки приложения силы трения $T(U)$ в месте контакта тела массы m с лентой; ${{k}_{0}}$– коэффициент демпфирования; ${{c}_{0}}x + {{c}_{1}}{{x}_{{\tau }}}$ и $f(x)$ – соответственно линейная и нелинейная части силы упругости пружины; ${{c}_{0}} = {\text{const}}$, ${{c}_{1}} = {\text{const}}$, ${{x}_{{\tau }}} = x{\kern 1pt} {\kern 1pt} (t - {\tau })$, ${\tau } = {\text{const}}$ – запаздывание; J – суммарный момент инерции вращающихся частей; $M({\dot {\varphi }})$ – разность вращающего момента источника энергии и момента сил сопротивления вращению, ${\dot {\varphi }}$ – скорость вращения двигателя.

Характеристика силы трения широко распространена на практике в форме T(U) = = $R(\operatorname{sgn} U - {{\alpha }_{1}}U + {{\alpha }_{3}}{{U}^{3}})$. Такая форма наблюдается также при рассмотрении проблемы измерения сил трения в космических условиях [19]. Представим ее в виде

где $R$ – нормальная сила реакции; $\operatorname{sgn} U = 1$ при $U > 0$ и $\operatorname{sgn} U = - 1$ при $U < 0$, ${{\alpha }_{1}}$ и ${{\alpha }_{3}}$ – постоянные, ${{\delta }_{0}} = --{{\alpha }_{1}}V + {{\alpha }_{3}}{{V}^{3}}$, ${{\delta }_{1}} = {{\alpha }_{1}} - 3{{\alpha }_{3}}{{V}^{2}}$, ${{\delta }_{2}} = 3{{\alpha }_{3}}V$, ${{\delta }_{3}} = - {{\alpha }_{3}}$.

Использование линейных характеристик в расчетах сил различной природы часто связано с решением уравнений, хотя в реальных условиях эти характеристики являются нелинейными. На практике при построении расчетных моделей они часто бывают неизвестными и в большинстве случаев представляются полиномиальными функциями. Представим нелинейную часть силы упругости $f(x)$ полиномом

где ${{{\gamma }}_{j}} = {\text{const}}$.

По методу прямой линеаризации [14] нелинейные функции $F(\dot {x})$ и $f(x)$ заменим линейными функциями

где ${{B}_{F}}$, ${{k}_{F}}$, ${{B}_{f}}$, ${{k}_{f}}$ являются коэффициентами линеаризации, определяемыми выражениями:

а) $F(\dot {x})$

б) $f(x)$

Здесь $a = \max \left| x \right|$, $\upsilon = \max \left| {\dot {x}} \right|$ и символ r представляет параметр точности линеаризации. Как показано в работе [14], параметр r может принимать различные значения, но может быть выбран из интервала (0, 2).

Нелинейную характеристику источника энергии можно представить полиномом

Тогда линеаризованная характеристика источника будет иметь форму ${{M}_{*}}({\dot {\varphi }}) = {{B}_{M}}$ + ${{k}_{M}}{\dot {\varphi }}$ с коэффициентами

где ${{\Omega }_{*}}$ – максимальное значение скорости Ω источника энергии.

Уравнения (1) с учетом линеаризации функций принимают вид

где $k = {{k}_{0}} - R{{k}_{F}}$, $c = {{c}_{0}} + {{k}_{f}}$, $B = R{{B}_{F}} - {{B}_{f}}$.

3. Решение уравнения (6) можно построить двумя методами [14], одним из которых является метод замены переменных с усреднением. Он позволяет рассмотреть стационарные и нестационарные процессы как в области резонанса, так и ее близких окрестностях, в которых возникают почти периодические колебания.

В [14] для нелинейного уравнения вида $\ddot {x} + \bar {F}(\dot {x}) + \bar {f}(x) = H(t,x)$, с нелинейными функциями $\bar {F}(\dot {x})$ и $\bar {f}(x)$, линеаризованными по методу прямой линеаризации с коэффициентами k и ${{{\omega }}^{2}}$ аналогично форме (4), с использованием замены переменных $x = \upsilon {{p}^{{ - 1}}}\cos {\psi }$, $\dot {x} = - \upsilon \sin {\psi }$, ${\psi } = pt + {\xi }$, $\upsilon = \max \left| {\dot {x}} \right|$ (в зависимости от функции $H(t,x)$ символ p может отражать как частоту внешнего воздействия, так и частоту автоколебаний), в результате применения усреднения в системе, выведенной на основе замены переменных, для определения нестационарных значений $\upsilon $ и ξ получаются стандартной формы уравнения

где

Рассмотрим процедуру построения решения уравнения источника энергии, которое в общем случае запишем в виде

Представим теперь (8) посредством замены ${\dot {\varphi }} = {\theta }$ в форме

или с учетом линеаризации характеристики источника энергии – в форме

Полагая ${\theta } = \Omega + {\tilde {\varepsilon }}$, где Ω – главная часть решения, ${\tilde {\varepsilon }}$ – не учитываемые в дальнейшем малые вибрационные составляющие, и применив процедуру усреднения за период к уравнению (9а), получим

где

С учетом замены $M(\Omega )$ на ${{B}_{M}} + {{k}_{M}}{\kern 1pt} \Omega $ в (10), будем иметь выражение для случая линеаризации характеристики источника энергии и, для краткости, приведем лишь соотношения на основе (10).

Условия $d\upsilon {\text{/}}dt = 0$, $d{\xi /}dt = 0$, $d\Omega {\text{/}}dt = 0$ дают уравнения стационарных движений

Уравнения (7) и (10) позволяют изучить нестационарные процессы, а уравнения (11) определить характеристики стационарных колебаний. Амплитуда колебаний определяется выражением $a = \upsilon {{p}^{{ - 1}}}$. Уравнения (7) с учетом данного выражения можно преобразовать к виду, зависимому от амплитуды

4. На основе выражений (7), (10) для уравнения (6) можно выписать соотношения, дополняя влияние запаздывания. Вычислив 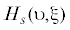, 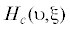с учетом ${{x}_{{\tau }}} = \upsilon {{{\nu }}^{{ - 1}}}\cos ({\psi } - {\nu \tau })$ и подставив в (7) вместо частоты p частоту ν, получим уравнения для определения нестационарных значений а, ξ , u

а) $u \geqslant a{\kern 1pt} {\nu }$

б) $u < a{\kern 1pt} {\nu }$

где ${{{\omega }}^{2}} = {c \mathord{\left/ {\vphantom {c m}} \right. \kern-0em} m} = {\omega }_{0}^{2} + {{k}_{f}}(a){{m}^{{ - 1}}}$, ${\omega }_{0}^{2} = {{{{c}_{0}}} \mathord{\left/ {\vphantom {{{{c}_{0}}} m}} \right. \kern-0em} m}$, $u = {{r}_{0}}\Omega $, ${{{\psi }}_{*}} = 2{\pi } - \arcsin ({u \mathord{\left/ {\vphantom {u {a{\nu })}}} \right. \kern-0em} {a{\nu })}}$.

При $\dot {\upsilon } = 0$, ${\dot {\xi }} = 0$ из первых двух уравнений (12) получим соотношения для определения амплитуды автоколебаний. В случае $u < a{\nu }$ амплитуда определяется приближенным выражением $a \approx {u \mathord{\left/ {\vphantom {u {\nu }}} \right. \kern-0em} {\nu }}$.

Следующие уравнения позволяют определить стационарные значения скорости u

а) $u \geqslant a{\kern 1pt} {\nu }$

б) $u < a{\kern 1pt} {\nu }$

где ${{S}_{ + }}(u) = {{r}_{0}}R(1 + {{B}_{F}})$, ${{S}_{ - }}(u) \approx {{r}_{0}}R[1 + {{B}_{F}} - {{{\pi }}^{{ - 1}}}(3{\pi } - 2{{{\psi }}_{*}})]$.

Из системы (12) при малой расстройке частот ${{{\omega }}_{0}} - {\nu }\sim {\varepsilon }$, где ε – достаточно малая величина, будем иметь уравнения гармонического захватывания. А если расстройка не мала, то уравнения (12) позволяют рассмотреть почти периодические колебания посредством их численного интегрирования. С помощью системы (12) можно вывести условия устойчивости колебаний на основе критериев Рауса–Гурвица.

В работе [14] приведено сравнение результатов, полученных методами прямой линеаризации и известными методами, и показано, что они полностью совпадают качественно. Имеются лишь небольшие количественные отличия (отсутствующие в ряде случаев), которые приведены в [14] при различных значениях параметра точности линеаризации. Нелинейное уравнение вида (1) подробно изучено в [17]. Останавливаться на анализе уравнений (12) и условиях устойчивости колебаний не будем, т.к. целью настоящей статьи является описание процедуры применения методов прямой линеаризации для расчета нелинейных колебательных систем с источниками энергии ограниченной мощности.