Проблемы машиностроения и надежности машин, 2020, № 2, стр. 16-24
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ, ПОГРУЖЕННОЙ В ЖИДКОСТЬ
О. И. Косарев 1, А. К. Пузакина 1, *, Д. Ф. Нахатакян 1
1 Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия
* E-mail: alla-puzakina@yandex.ru
Поступила в редакцию 05.07.2019
Принята к публикации 25.12.2019
Аннотация
Предложен численно-аналитический метод расчета вынужденных колебаний оболочечной конструкции, погруженной в жидкость. Конструкция состоит из набора конечных упругих цилиндрических оболочек и упругих колец, к которым приложены сосредоточенные дискретные возмущающие силы. Приведены примеры сравнительного расчета амплитудно-частотных характеристик и форм колебаний оболочечной конструкции в вакууме и в жидкости.
Рассматривается задача о вынужденных колебаниях оболочечной конструкции со свободными граничными условиями на торцах, погруженной в жидкость. Конструкция состоит из секций, каждая из которых представляет собой конечную упругую цилиндрическую оболочку с упругими кольцами на концах. На оболочечную конструкцию действуют дискретные вынуждающие силы. Попытки решения этой задачи методом конечных элементов по ряду причин нельзя признать успешными [7]. Численно-аналитические методы расчета колебаний конечных цилиндрических оболочек в жидкости до сих пор не разработаны [1–9] и решение этой задачи является актуальным.
Цель – разработать численно-аналитический метод расчета вынужденных колебаний цилиндрических оболочек в жидкости.
Идея предлагаемого метода расчета состоит в следующем. Система условно разбивается на подсистемы, включающие оболочки и кольца. Для каждой оболочки составляются дисперсионные уравнения и определяются их корни. Решение свободных колебаний оболочки записывается в виде вектора (матрицы-столбца) перемещений (u, ${v}$, w, w'). Функции распределения перемещений оболочек по их длине записываются через перемещения торцевых сечений. Внутренние силы в оболочках приводятся к торцам оболочек. Определяются матрицы динамических жесткостей колец по тем же четырем перемещениям. Общее матричное уравнение вынужденных колебаний всей оболочечной конструкции записывается так же, как для цепной системы. Вынуждающие силы приложены к кольцам и распределены по окружному углу φ по гармоническому закону P = pcosnφ. Дискретные вынуждающие силы могут задаваться в любом месте по длине цилиндрической оболочки без применения δ-функции. Получается матричное уравнение ленточного типа, состоящее из блок-матриц четвертого порядка, диагонально расположенных в общей матрице. Это позволяет упростить составление и ускорить решение сводных матричных уравнений высокого порядка (нескольких сотен).
Уравнения движения цилиндрической оболочки в перемещениях, основанные на моментной теории упругих оболочек Кирхгофа–Лява, имеют вид [8]
(1)
$\frac{{\partial {{T}_{2}}}}{{\partial \varphi }} + \frac{{\partial S}}{{\partial \xi }} + \frac{1}{a}\left( {\frac{{\partial {{M}_{2}}}}{{\partial \varphi }} + 2\frac{{\partial H}}{{\partial \xi }}} \right) - {\text{ }}\rho _{*}^{{}}ha\frac{{{{\partial }^{2}}v}}{{\partial {{t}^{2}}}} + {{q}_{2}}a = 0,$Решения уравнений свободных колебаний конечной цилиндрической оболочки (1) записываются в форме [9]
(2)
$\begin{gathered} u{\text{ }} = {\text{ }}U\cos (n\varphi ){{e}^{{i\omega t}}},\quad {v} = V\sin (n\varphi ){{e}^{i}}^{{\omega t}},\quad w = W\cos (n\varphi ){{e}^{i}}^{{\omega t}}, \\ U = {\text{ }}\sum\limits_{j = 1}^8 {{{C}_{{jn}}}} \frac{{\Delta _{{jn}}^{{\left( 2 \right)}}}}{{\Delta _{{jn}}^{{\left( 1 \right)}}}}{{e}^{{i{{\alpha }_{{jn}}}\xi }}},\quad V = \sum\limits_{j = 1}^8 {{{C}_{{jn}}}} \frac{{\Delta _{{jn}}^{{\left( 3 \right)}}}}{{\Delta _{{jn}}^{{\left( 1 \right)}}}}{{e}^{{i{{\alpha }_{{jn}}}\xi }}},\quad W = \sum\limits_{j = 1}^8 {{{C}_{{jn}}}} {{e}^{{i{{\alpha }_{{jn}}}\xi }}}, \\ \end{gathered} $В результате подстановки этих решений в уравнение (1) получим уравнение свободных колебаний оболочки в матричном виде [10]
(3)
$\left[ {\begin{array}{*{20}{c}} {{{L}_{{11}}} + \omega _{*}^{2}}&{{{L}_{{12}}}}&{{{L}_{{13}}}} \\ { - {{L}_{{12}}}}&{{{L}_{{22}}} + \omega _{*}^{2}}&{{{L}_{{23}}}} \\ { - {{L}_{{13}}}}&{{{L}_{{23}}}}&{{{L}_{{33}}} + \omega _{*}^{2}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} U \\ V \\ W \end{array}} \right\} = \frac{a}{q}\left\{ {\begin{array}{*{20}{c}} 0 \\ 0 \\ {{{p}_{s}}} \end{array}} \right\}.$Дисперсионное уравнение для конечной цилиндрической оболочки, погруженной в жидкость, имеет вид
(4)
$\frac{{{{\Delta }_{0}}(\alpha )}}{{{{\Delta }^{1}}(\alpha )}} - \frac{{{{\rho }_{0}}{{\omega }^{2}}aH_{n}^{{(2)}}(ka)}}{{qkH_{n}^{{(2)}}{\text{'}}(ka)}} = 0,$(5)
$\begin{gathered} - \;{{k}_{{22}}}{{b}_{{33}}} + 2{{k}_{{23}}}{{b}_{{23}}} + {{\mu }^{2}}{{k}_{{22}}} - {{b}_{{11}}}{{b}_{{22}}}{{\delta }^{2}} - {{b}_{{11}}}{{k}_{{22}}}{{k}_{{33}}} + 2i\mu k{}_{{12}}{{k}_{{23}}} + {{b}_{{11}}}k_{{23}}^{2}, \\ {{A}_{2}} = - \left( {1 + {{k}_{{22}}} + {{k}_{{33}}}} \right)\omega _{*}^{2} + (k_{{12}}^{2} - 2{{k}_{{23}}}{{b}_{{23}}} - {{\mu }^{2}} + {{b}_{{33}}} + {{b}_{{11}}}{{k}_{{33}}} + {{b}_{{22}}}{{k}_{{33}}} + \\ \end{gathered} $Для составления уравнений вынужденных колебаний оболочечной конструкции, состоящей из набора оболочек, соединенных между собой кольцами, каждое уравнение движения записывается для перемещений трех соседних подсистем с номерами: k-текущей, k – 1-предыдущей и k + 1-последующей. Подсистемами являются оболочки и кольца. Внутренние силы оболочки, приложенные, например, к кольцу k, выражаются через перемещения концов оболочек, присоединенных к кольцу слева (в конце предыдущей оболочки k – 1) и справа (в начале последующей оболочки k + 1).
Определим перемещения торцевых сечений оболочек. Представим распределение перемещений по длине y для каждой оболочки с учетом дополнительной координаты w' = dw/dy в матричном виде
(6)
${{\zeta }_{{(y)}}} = \left| \begin{gathered} u \\ v \\ w \\ w{\text{'}}{\kern 1pt} \\ \end{gathered} \right| = \left[ {\begin{array}{*{20}{c}} {\frac{{\Delta _{{}}^{{\left( 2 \right)}}\left( {{{\alpha }_{1}}} \right)}}{{\Delta _{{}}^{{\left( 1 \right)}}\left( {{{\alpha }_{1}}} \right)}}}&{\frac{{\Delta _{{}}^{{\left( 2 \right)}}\left( {{{\alpha }_{2}}} \right)}}{{\Delta _{{}}^{{\left( 1 \right)}}\left( {{{\alpha }_{2}}} \right)}}}& \cdots &{\frac{{\Delta _{{}}^{{\left( 2 \right)}}\left( {{{\alpha }_{8}}} \right)}}{{\Delta _{{}}^{{\left( 1 \right)}}\left( {{{\alpha }_{8}}} \right)}}} \\ {\frac{{\Delta _{{}}^{{\left( 3 \right)}}\left( {{{\alpha }_{1}}} \right)}}{{\Delta _{{}}^{1}\left( {{{\alpha }_{1}}} \right)}}}&{\frac{{\Delta _{{}}^{{\left( 3 \right)}}\left( {{{\alpha }_{2}}} \right)}}{{\Delta _{{}}^{1}\left( {{{\alpha }_{2}}} \right)}}}& \cdots &{\frac{{\Delta _{{}}^{{\left( 3 \right)}}\left( {{{\alpha }_{8}}} \right)}}{{\Delta _{{}}^{1}\left( {{{\alpha }_{8}}} \right)}}} \\ 1&1& \cdots &1 \\ {i{{\alpha }_{1}}}&{i{{\alpha }_{2}}}& \cdots &{i{{\alpha }_{8}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{e}^{{i{{\alpha }_{1}}y}}}}&0&0& \cdots &0 \\ 0&{{{e}^{{i{{\alpha }_{2}}y}}}}&0& \cdots &0 \\ 0&0&{{{e}^{{i{{\alpha }_{3}}y}}}}& \cdots &0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0&0&0& \cdots &{{{e}^{{i{{\alpha }_{8}}y}}}} \end{array}} \right]{\kern 1pt} \,\left| {\begin{array}{*{20}{c}} {{{{\text{C}}}_{1}}} \\ {{{{\text{C}}}_{2}}} \\ {{{{\text{C}}}_{3}}} \\ \vdots \\ {{{{\text{C}}}_{8}}} \end{array}} \right|.$Дополнительная координата w' введена для возможности формирования блок-матриц в уравнениях стыковки цилиндрических оболочек с кольцами по четырем основным силовым факторам. Выражение (6) используются для каждой оболочки при составлении системы уравнений движения для всей оболочечной конструкции в целом. Обозначим A(y) произведение матриц в правой части выражения (6)
Представим перемещения торцев оболочки, имеющей длину $\ell $, в начале при y = 0 и в конце y = $\ell $ в виде
Составим блок-матричное уравнение
Из этого уравнения определим вектор-столбец коэффициентов W0= {С1 – С8}
Текущие перемещения по длине оболочки, выраженные через перемещения ее торцов, определяются выражением
Таким образом, вектор перемещений оболочки с произвольным номером k
(7)
${{\zeta }_{K}}\left( y \right) = {{\{ {{u}_{k}},{{v}_{k}},{{w}_{k}},w_{k}^{'}\} }^{T}} = G_{k}^{{}}\left( y \right)\left[ {C_{k}^{1}\left( {{{\zeta }_{{k0}}}} \right) + C_{k}^{2}\left( {{{\zeta }_{{k\ell }}}} \right)} \right],$Матрица Gk(y) размером 4 × 8 состоит из столбцов Gpk, в которых р = 1, 2, …. 8 по числу корней дисперсионного уравнения.
Матрицы $C_{k}^{1}$, $C_{k}^{2}$ являются блоками размером 8 × 4 квадратной матрицы Ck размером 8 × 8
Приведем внутренние силы в оболочке к ее торцевым сечениям. Вектор-столбец внутренних сил в оболочке номера k имеет вид
Соответствие между этими внутренними силами и перемещениями оболочки следующее
Связь внутренних сил оболочки с перемещениями торцевых сечений оболочки может быть представлена вектором
В случае, когда к кольцу (слева и справа) крепятся оболочки разного диаметра, необходимо выполнить соответствующее приведение координат (перемещений) торцов оболочек к центру масс поперечного сечения кольца. Векторы перемещений торцов оболочки
внутренние силы, действующие в торцевых сечениях оболочек (в конце предыдущей оболочки ηk,l и в начале последующей оболочки ηk + 1, 0), приведем к соединяющему их кольцу с помощью матриц приведения $H_{k}^{3}$ и $H_{k}^{4}$. Силы, приложенные к центру масс поперечного сечения кольца c номером k
(8)
$F_{k}^{{(1)}} = H_{k}^{3}\eta _{{k,1}}^{{}},\quad F_{k}^{{(2)}} = H_{k}^{4}\eta _{{k + 1,0}}^{{}}.$Матричное уравнение движения оболочечной конструкции формируется следующим образом. С учетом принятых обозначений уравнение движения кольца номера k в матричной форме имеет вид
где Pk – вектор возмущающих сил; $F_{k}^{{(1)}}$, $F_{k}^{{(2)}}$ – векторы внутренних сил, приложенные от оболочек к кольцу слева и справа; Мk – матрица динамических жесткостей кольца номера k.Подставляя в уравнение движения кольца (9) значения сил (8) и перемещений оболочек (7), получим систему уравнений порядка 4(N + 1), где N – общее количество оболочек; N + 1 – общее количество колец. В уравнениях движения порядковые номера колец обозначим q, где 0 ≤ q ≤ p. Уравнения составляются для каждого кольца последовательно.
Уравнения для первого кольца q = 0, для каждого промежуточного кольца от q = 1 до q = N – 1 и для последнего кольца q = N имеют вид
(10)
$\begin{gathered} H_{q}^{3}G_{q}^{*}\left( {{{\ell }_{q}}} \right)C_{q}^{1}H_{{q - 1}}^{2}Z_{{q - 1}}^{{}} + [M_{q}^{{}} + H_{q}^{3}G_{q}^{*}\left( {{{\ell }_{q}}} \right)C_{q}^{2}H_{q}^{1} - H_{q}^{4}G_{{q + 1}}^{*}\left( 0 \right){\text{ }}C_{{q + 1}}^{1}H_{q}^{2}]{{Z}_{q}} - \\ - \;H_{q}^{4}G_{{q + 1}}^{*}\left( 0 \right)C_{{q + 1}}^{2}H_{{q + 1}}^{1}{{Z}_{{q + 1}}} = {{P}_{q}}, \\ \end{gathered} $Общее матричное уравнение для оболочечной конструкции имеет ленточную диагональную структуру расположения блок-матриц размером 4 × 4 и в сумме может иметь порядок нескольких сотен. В результате решения этой системы определяются искомые векторы перемещений колец Zq.
После определения векторов перемещений Zq на кольцах q из уравнения (10) можно построить амплитудно-частотные характеристики колебаний в заданных сечениях (кольцах) оболочечной конструкции, а также формы вынужденных колебаний для каждой оболочки и всей оболочечной конструкции в целом.
Форма колебаний для каждой оболочки определяется выражением
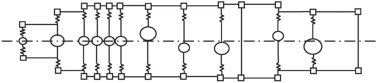
Метод расчета реализован в виде алгоритмов и компьютерных программ, написанных на языке Fortran, применительно к динамической модели, показанной на рис. 1. Ниже приведены результаты расчетной оценки влияния присоединенной жидкости на АЧХ и формы колебаний оболочек в вакууме (“сухой”) и в жидкости (“мокрой”), что представляет теоретический и практический интерес. Для чистоты эксперимента принята упрощенная модель оболочечной конструкции, состоящей из соединенных между собой восьми одинаковых секций, состоящих из цилиндрических оболочек постоянного радиуса и колец. Конструктивные параметры составной оболочки: общая длина L = 70 м; радиус а = 4 м; толщина h = 0.04 м. Материал – сталь. Возмущающая сила P = 1000 Н приложена на левом конце оболочечной конструкции.
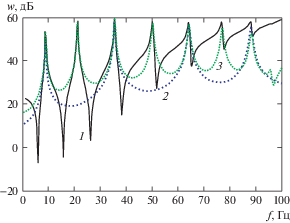
На рис. 2–4 приведены результаты расчетов АЧХ и форм колебаний в диапазоне частот f = 1–100 Гц для окружной гармоники n = 1. На рис. 2 приведены АЧХ радиальных колебаний w в dB составной оболочки в вакууме. Три линии на рис. 2 – сплошная, точками и штриховая соответствуют АЧХ в сечениях: 1 – левый конец; 2 – середина; 3 – правый конец оболочечной конструкции. Первые три резонансные частоты изгибных колебаний оболочки на рис. 2: f = 8.75 Гц; 28.25 Гц; 35.5 Гц.
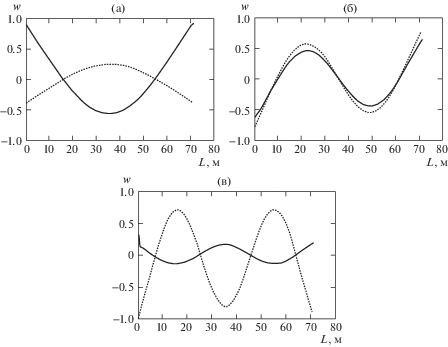
Рис. 4.
Формы резонансных колебаний оболочки в жидкости на частотах: (а) f = 4 Гц; (б) f = 9.25 Гц; (в) f = 14.25 Гц.
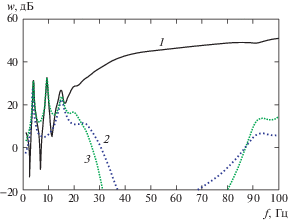
На рис. 3 приведены АЧХ колебаний той же оболочки в жидкости в том же диапазоне частот. Первые три резонансные частоты уменьшились и стали: f = 4 Гц; f = 9.25 Гц; f = 14.25 Гц. Уровни колебаний на соответствующих резонансных частотах существенно снизились, примерно на 20–30 dB. В оболочке, погруженной в жидкость, резонансы на частотах выше 14.7 Гц вообще не проявились (задемпфировались).
На рис. 4 приведены формы радиальных колебаний W оболочки в жидкости соответственно на первых трех резонансных частотах: а) f = 4 Гц; б) f = 9.25 Гц; в) f = 14.25 Гц. Сплошные линии – реальные составляющие Re(W), пунктирные линии – мнимые составляющие Im(W) комплексного радиального перемещения w. Полученные формы колебаний соответствуют типичным низшим формам изгибных колебаний оболочки и балки со свободными краями, что подтверждает правильность расчетов. Резонансные (собственные) формы колебаний оболочек в вакууме и в жидкости полностью совпадают, что является подтверждением правильности расчета оболочки в жидкости. Результаты расчетной оценки влияние жидкости на резонансные частоты (их величины) получены впервые. Это влияние оказалось весьма существенным, что является новым и принципиально важным результатом.
Список литературы
Forsberg K. Influence of boundary conditions on the modal characteristics of thin cylindrical shells // AIAA Journal. V. 2. № 12. Dec. 1964. P. 2150.
Скенк Г.А., Бентхайн Дж. В. Эффективное вычисление и визуализация дисперсионных кривых для тонкой цилиндрической оболочки, погруженной в жидкость // Акустический журнал. 1995. № 5. С. 828.
Авербух А.З., Вейцман Р.И., Генкин М.Д. Колебания элементов конструкций в жидкости. М.: Наука, 1987. 158 с.
Музыченко В.В., Рыбак С.А. Импеданс излучения ограниченной цилиндрической области // Акустический журнал. 1990. № 5. С. 898.
Романов В.Н., Иванов В.С. Излучение звука элементами судовых конструкций. СПб.: Судостроение, 1993. 212 с.
Болотин В.В. Неконсервативные задачи теории упругой устойчивости. М.: Гос. изд. ФМЛ, 1961. С. 221.
Коротин П.И., Салин Б.М., Суворов А.С. Вопросы численного моделирования рассеяния акустических волн на телах сложной формы с использованием метода конечных элементов // Сб. трудов XX сессии РАО. Т. 1. М.: ГЕОС, 2008. С. 169.
Бидерман В.Л. Механика тонкостенных конструкций. Статика. М.: Машиностроение, 1977. С. 260.
Прочность. Устойчивость. Колебания. Т. 3. Справочник / Под ред. И.А. Биргера и Я.Г. Пановко. М.: Машиностроение, 1968. С. 423.
Косарев О.И. Дисперсионное уравнение свободной конечной цилиндрической оболочки, погруженной в жидкость // Проблемы машиностроения и надежности машин. 2019. № 5. С. 36.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин