Проблемы машиностроения и надежности машин, 2020, № 2, стр. 46-53

В работах по устойчивости Е.Л. Николаи [1] впервые обнаружил, что при исследовании устойчивости положения равновесия механических систем для критических значений некоторых нагрузок системы не имеют смежных положений равновесия и изначально устойчивое исходное положение равновесия сменяется на колебательное движение. Указанный факт имеет место при действии неконсервативных нагрузок и для исследования устойчивости требует применения динамического метода исследования [2]. Гидро- и аэродинамические силы, реактивные силы, силы, действующие на роторы турбин, электрических машин и т.д. не являются консервативными и при достижении ими критических значений могут быть источником притока энергии при колебательных движениях системы. Это соответствует потере устойчивости исходного положения равновесия системы колебательным образом по типу флаттер. В теории устойчивости механических систем помимо эйлерова подхода к исследованию устойчивости элементов конструкций оформился специальный класс задач, а именно неконсервативные задачи теории упругой устойчивости. В настоящее время решено большое количество неконсервативных задач устойчивости [2–8], исследована устойчивость разнообразных механических систем, находящихся в условиях сложного нагружения различными силами, в том числе и неконсервативными. Характерной особенностью неконсервативных систем является большое количество особенностей, не свойственных системам при нагружении потенциальными силами. Можно назвать возможность потери устойчивости по типу дивергенция, по типу флаттера; невыпуклость области устойчивости, если она построена в пространстве параметров нагрузок; существенное взаимодействие различных форм колебаний.

Наиболее интересной и трудно объяснимой особенностью неконсервативных задач теории упругой устойчивости является дестабилизирующее влияние демпфирования на критические значения нагрузок [7–16]. Действительно, увеличение рассеяния энергии в динамических системах при вибрационных, ударных, параметрических и подобного рода нагрузках оказывает положительное влияние на показатели механической надежности. В задачах устойчивости конструкций и деталей машин при действии неконсервативных позиционных сил учет демпфирования, в некоторых случаях весьма малого, может существенно снижать критические значения параметров нагружения. Эта особенность, называемая парадоксом Циглера, впервые была изложена в работе [7].

За время с момента обнаружения парадокса Циглера появилось большое количество работ, в которых авторы пытаются объяснить дестабилизирующее влияние диссипативных сил на критические значения некоторых неконсервативных нагрузок [8–16]. И по уровню убедительности, и по уровню понимания эти объяснения весьма разнообразны. Чаще всего подобного рода работы сводятся к демонстрации зависимостей критических значений нагрузок от величины диссипации энергии в неконсервативной системе различного происхождения, просто подтверждая тем самым парадокс Циглера.

В настоящей статье для ряда традиционных неконсервативных задач теории упругой устойчивости, в частности, двухзвенного маятника при действии следящей нагрузки, задачи Бека (консольный стержень с распределенными параметрами при действии следящей силы) и флаттера плоской панели в сверхзвуковом потоке газа, проводится систематическое исследование влияния демпфирования на критические величины параметров нагрузок.

Двухзвенный маятник. Начнем с исследования маятника Циглера, т.е. двухзвенного маятника, несущего сосредоточенные массы ${{m}_{1}}$ и ${{m}_{2}}$ и перемещения которого имеют место в одной плоскости. Маятник находится под действием следящей силы $P$. Будем исследовать на устойчивость прямолинейную форму равновесия, когда упругие шарниры с коэффициентами жесткости ${{c}_{1}}$ и ${{c}_{2}}$ не нагружены. Кроме того, повороты в шарнирах сопровождаются рассеянием энергии с коэффициентами ${{b}_{1}}$ и ${{b}_{2}}$. За обобщенные координаты примем углы отклонений безынерционных стержней от прямолинейной формы ${{\varphi }_{1}}$ и ${{\varphi }_{2}}$. Линеаризованные уравнения возмущенного движения системы относительно вектора угловых перемещений $\varphi = {{\left[ {{{\varphi }_{1}},{{\varphi }_{2}}} \right]}^{{\text{T}}}}$ запишем в виде

где обозначено

В уравнении (1) принято ${{m}_{1}} = 2{{m}_{2}} \equiv 2m$, ${{c}_{1}} = {{c}_{2}} \equiv c$, ${{l}_{1}} = {{l}_{2}} \equiv l$ и введены безразмерные параметры

Поставив целью исследование зависимости критического значения параметра следящей силы ${{\beta }_{*}}$ от параметров рассеяния энергии, представим вектор $\varphi $ в виде $\varphi (\tau ) = \Phi {{{\text{e}}}^{{\lambda \tau }}}$, где $\lambda $ – характеристический показатель, определяющий поведение системы после начальных возмущений. По теории Ляпунова система устойчива, если $\forall \operatorname{Re} \lambda \leqslant 0$. Характер потери устойчивости определяется способом пересечения характеристическими показателями мнимой оси при переходе в правую полуплоскость. В рассмотренных задачах переход характеристических показателей в правую полуплоскость при достижении нагрузкой критического значения происходит с отличными от нуля мнимыми частями. Таким образом, потеря устойчивости происходит колебательным образом по типу флаттер. С учетом (1) для показателей $\lambda $ получим уравнение

Критическое значение ${{\beta }_{*}}$ из уравнения (2) можно получить либо непосредственным решением этого уравнения, либо определив наименьший корень главного минора матрицы Гурвица. Некоторые результаты исследования зависимости критического значения параметра следящей силы от параметров демпфирования представлены на рис. 1.

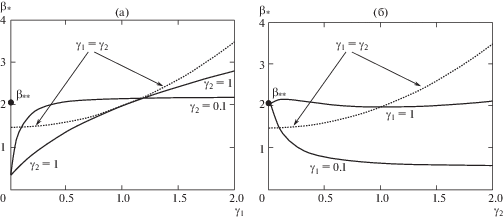
Квазикритическое значение следящей силы $\beta $, вычисленное без учета демпфирования, с матрицей ${\mathbf{B}}$, приравненной нулю, равно ${{\beta }_{{{\text{**}}}}} = 2.09$. При исчезающе малом, но одинаковом трении в каждом шарнире, т.е. ${{\gamma }_{1}} = {{\gamma }_{2}} \to 0$, критическое значение снижается до ${{\beta }_{*}} = 1.47$. В этом и состоит парадокс Циглера. С увеличением демпфирования, но с сохранением условия ${{\gamma }_{1}} = {{\gamma }_{2}}$ дестабилизирующего влияния трения на устойчивость системы не наблюдается [8] и кривая зависимости ${{\beta }_{*}}({{\gamma }_{\alpha }})$ (пунктирные кривые) на рис. 1 при ${{\gamma }_{1}} = {{\gamma }_{2}}$ монотонно возрастают. Этот факт не означает, что квазикритическое значение следящей силы вообще не реализуется. Неравномерность распределения демпфирования по степеням свободы вносит в кривые ${{\beta }_{*}}({{\gamma }_{\alpha }})$ широкое разнообразие. На рис. 1а фиксированные значения диссипации энергии во втором шарнире (${{\gamma }_{2}} = 0.1$ и ${{\gamma }_{2}} = 1$) при весьма малых значениях существенно снижают ${{\beta }_{*}}$. Далее кривые ${{\beta }_{*}}({{\gamma }_{1}})$ возрастают с различным характером, зависящим от величины ${{\gamma }_{2}}$.

При фиксированных значениях диссипации энергии в первом шарнире (${{\gamma }_{1}} = 0.1$ и ${{\gamma }_{1}} = 1$) и при ${{\gamma }_{2}} \to 0$ (рис. 1б) реализуется квазикритическое значение следящей силы ${{\beta }_{{{\text{**}}}}}$. А далее с ростом ${{\gamma }_{2}}$ кривые ${{\beta }_{*}}({{\gamma }_{1}})$ могут убывать, как это происходит при ${{\gamma }_{1}} = 0.1$, или вести себя немонотонно (${{\gamma }_{1}} = 1$), имея даже некоторый минимум. Этот минимум можно пояснить поведением характеристических показателей. Здесь один из характеристических показателей ${{\lambda }_{2}}$ несколько раз пересекает мнимую ось.

Задача Бека. Обратимся теперь к системе с распределенными параметрами. Из линейных моделей рассеяния энергии рассмотрим внешнее трение, пропорциональное скорости перемещения точек упругой системы, и внутреннее трение в материале по схеме Фойхта. Рассмотрим известную задачу Бека – сжатие прямолинейного консольного стержня следящей силой. При общепринятых обозначениях уравнение возмущенного движения запишется в виде

где ${{b}_{i}}$ и ${{b}_{e}}$ коэффициенты внутреннего (модель Фойхта) и внешнего трения соответственно. Граничные условия имеют вид

С помощью безразмерных параметров

перепишем уравнение (3) и граничные условия (4) следующим образом

Однородную краевую задачу (6), (7) можно решить различными методами. Например, непосредственным интегрированием уравнения (6) с использованием условия наступления флаттера критическое значение параметра следящей силы можно определить путем сведения к задаче оптимизации [6]. Другой путь – сведение распределенной системы к конечномерной [2]. К таким методам можно отнести метод конечных элементов или метод разложения решения уравнения (6) $w(\xi ,\tau )$ в ряд по ортогональной системе функций. Для решения данной задачи в качестве такой системы функций примем формы собственных колебаний консольного стержня ${{\varphi }_{k}}\left( \xi \right)$, удовлетворяющие граничным условиям (7)

Подставляя это выражение в уравнение (6) и применяя процедуру метода Бубнова–Галеркина, получим систему обыкновенных дифференциальных уравнений относительно обобщенных координат ${{q}_{k}}\left( \tau \right)$. Матричную форму этих уравнений можно записать в виде

Матрицы ${\mathbf{A}}$, C и ${\mathbf{D}}$ размерностью $n \times n$, входящие в уравнение (9), вычисляются по формулам

Представляя вектор обобщенных координат с помощью характеристических показателей $\lambda $ в виде ${\mathbf{q}}\left( \tau \right) = {{{\mathbf{q}}}_{0}}\exp (\lambda \tau )$, приходим к матричному уравнению типа (2)

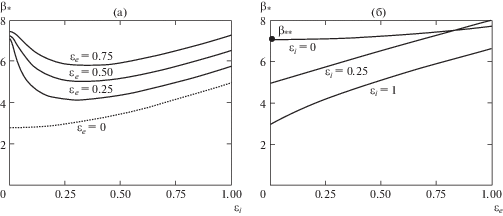
где обозначено

Результаты исследования зависимости критического значения следящей силы от параметров демпфирования представлены на рис. 2.

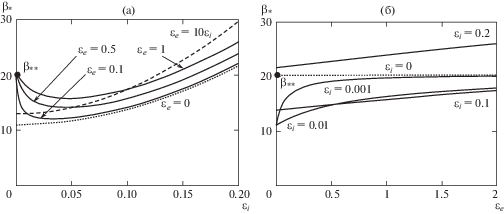
Как показано во многих работах, квазикритическое значение для задачи Бека, полученное при отсутствии какого-либо демпфирования, равно ${{\beta }_{{{\text{**}}}}} = 20.05$. Пунктирная линия на рис. 2а демонстрирует зависимость критического значения следящей силы от коэффициента внутреннего трения ${{\beta }_{{\text{*}}}}({{\varepsilon }_{i}})$ при отсутствии внешнего трения ${{\varepsilon }_{e}} = 0$. Начальное значение для ${{\varepsilon }_{i}}$ принято равным ${{10}^{{ - 10}}}$. Эта кривая монотонно возрастает, но ярко выраженный эффект дестабилизирующего влияния внутреннего трения проявляется в том, что эта кривая начинается из значения $10.95$, т.е. при ${{\varepsilon }_{i}} \to 0$ и ${{\varepsilon }_{e}} = 0$, так что критическое значение следящей силы почти в два раза меньше, чем квазикритическое. Штриховая линия соответствует пропорциональному росту и внутреннего трения в диапазоне ${{\varepsilon }_{i}} \in [{{10}^{{ - 10}}};0.2]$, и внешнего трения с сохранением соотношения ${{\varepsilon }_{e}} = 10{{\varepsilon }_{i}}.$

Исходя из значения ${{\beta }_{*}} = 12.89$, кривая ${{\beta }_{*}}({{\varepsilon }_{i}})$ также монотонно возрастает. Несколько иначе ведут себя кривые ${{\beta }_{*}}({{\varepsilon }_{i}})$ при некотором конечном значении внешнего трения ${{\varepsilon }_{e}}$. В частности, приняты значения ${{\varepsilon }_{e}} = 0.1$, ${{\varepsilon }_{e}} = 0.5$ и ${{\varepsilon }_{e}} = 1$. Эти кривые берут свое начало в окрестности квазикритического значения ${{\beta }_{{{\text{**}}}}}$ и имеют изолированный минимум, также оказывая в некотором диапазоне дестабилизирующее влияние на устойчивость стержня.

На рис. 2б в диапазоне ${{\varepsilon }_{e}} \in \left[ {0;2} \right]$ представлены зависимости критического значения следящей силы от внешнего трения ${{\beta }_{{\text{*}}}}({{\varepsilon }_{e}})$ при различных фиксированных значениях внутреннего трения. Из анализа рис. 2 следует, что дестабилизация имеет место лишь при малых значениях внутреннего трения.

Если внутреннее трение равно нулю ${{\varepsilon }_{i}} = 0$, то критическое значения следящей силы увеличивается. Однако эту зависимость (на рис. 2б для сравнения она изображена пунктирной линией) нельзя назвать сильной, т.к. при изменении ${{\varepsilon }_{e}}$ от 0 до 2 параметр критической силы изменяется от своего квазикритического значения ${{\beta }_{{{\text{**}}}}} = 20.05$ до ${{\beta }_{{{\text{**}}}}} = 20.26$, т.е. всего лишь на 1.05%.

Устойчивость панели. Далее рассмотрим флаттер плоской панели в потоке газа. При больших сверхзвуковых скоростях возмущенное давление $p$ на панель можно определить по приближенной формуле

где ${{p}_{0}}$ – невозмущенное давление; ${{\rho }_{\infty }}$ – плотность газа; $U$ – скорость набегающего потока; $v$ – скорость звука. Выражение в скобках в правой части представляет собой поперечную составляющую скорости частиц газа, обтекающего колеблющуюся панель. Как это делается в большом количестве работ, рассмотрим упругую плоскую панель (пластину) с толщиной $h$, шарнирно опертую по сторонам при $x = 0$ и $x = a$, удлиненную в направлении, ортогональном потоку. Это позволяет считать, что в пластине реализуется состояние цилиндрического изгиба, и нормальный прогиб в пластине $w\left( {x,t} \right)$ можно рассматривать как функцию только координаты $x$ и времени $t$.

Панель находится в сверхзвуковом потоке газа с невозмущенной скоростью $U$, направленной вдоль оси $Ox$. Приняв для упрощения равными внутреннее и внешнее невозмущенные давления, уравнение колебаний панели запишем в виде

Здесь $D$ – цилиндрическая жесткость панели; $\rho h$ – масса панели, отнесенная к единице площади; ${{b}_{i}}$ – коэффициент вязкоупругости для модели Фойхта,

Запишем уравнение (11) в безразмерном виде

где введены безразмерные параметры

Здесь ${{\omega }_{0}}$ первая собственная частота для шарнирно опертой по кромкам панели при цилиндрическом изгибе; ${{\varepsilon }_{i}}$ – безразмерный коэффициент внутреннего трения; ${{\varepsilon }_{e}}$ – безразмерный коэффициент аэродинамического трения.

Для решения задачи также применялся метод разложения по формам собственных колебаний. Уравнение возмущенного движения относительно обобщенных координат в данном случае примет вид

Здесь матрицы ${\mathbf{A}}$ и ${\mathbf{C}}$ вычисляются по формулам (10), а матрица ${\mathbf{B}}$ интегралом

Таким образом, для характеристических показателей имеем уравнение

На рис. 3а приведены зависимости критической скорости флаттера панели от внутреннего трения при различных значениях коэффициента аэродинамического трения ${{\varepsilon }_{e}}$. Монотонный рост критической скорости имеет место только для случая ${{\varepsilon }_{e}} = 0$ (пунктирная кривая). Если аэродинамическое трение не равно нулю, то зависимость ${{\beta }_{*}}({{\varepsilon }_{i}})$ имеет изолированный минимум в окрестности ${{\varepsilon }_{i}} \approx 0.3$. Дестабилизация проявляется при введении в систему внутреннего трения (рис. 3б).

Заключение. Таким образом, влияние демпфирования на критические значения весьма разнообразно. Для систем с конечным числом степеней свободы критические значения неконсервативных нагрузок также, как и явление дестабилизации существенно зависят от распределения диссипации по степеням свободы, в то время как для распределенных систем решающим фактором является природа диссипации энергии. Результаты исследований можно использовать в инженерных расчетах механических систем на устойчивость и при проектировании объектов современной техники.