Проблемы машиностроения и надежности машин, 2020, № 3, стр. 17-25

Наиболее важными показателями станочного оборудования являются максимально возможные ускорения перемещений инструмента относительно детали, рабочая зона и углы сервиса, а также точность позиционирования. Для повышения максимально возможных ускорений в манипуляторах в работе [1] предложено применение механизмов параллельной структуры, однако небольшие углы сервиса этих устройств существенно ограничивают их технологические возможности.

Ранее для более сложных механизмов в станочном оборудовании предлагалось применять вращательно-линейные мехатронные модули, перемещающие основания кинематических цепей трипода [2]. В ИМАШ РАН были предложены более сложные конструкции аналогичных механизмов с частичной кинематической развязкой, где применен вращательно-линейный привод [3]. Однако подобные механизмы структурно излишне сложны, что снижает точность позиционирования выходного звена. Применение совместного вращательно-поступательного синхронного электродвигателя с ротором в виде набора постоянных магнитов позволяет уменьшить число кинематических пар и упростить конструкцию механизма [4]. Такой электропривод вместе с датчиками положения составляет вращательно-поступательный мехатронный модуль. Исследования в этом направлении продолжаются [5–7], однако эти модули пока не нашли широкого применения из-за конструктивной сложности. Полностью исключить влияние механических эффектов на позиционирование невозможно из-за необходимости применения вращательно-линейных подшипников. В то же время может иметь место электромагнитное взаимодействие, связанное с вихревыми токами в роторе. Поэтому целесообразно собрать аналогичный модуль из комплектующих, производимых серийно, используя синхронные электродвигатели [8 ] .

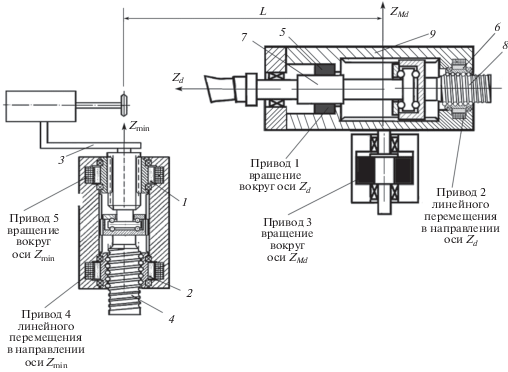
1. Пятикоординатный робот-станок на основе вращательно-линейных модулей. Вращательно-линейный модуль включает шлицевую втулку 1 (рис. 1), которая передает вращение двигателя и обеспечивает вращательное движение выходного объекта манипулирования. Внутренний вал шлицевой втулки кроме вращения позволяет выполнять линейное перемещение. Линейное перемещение осуществляется через шариковинтовую пару 2, 4 (рис. 1), преобразующую вращательное движение двигателя в линейное перемещение выходного вала.

На базе вращательно-линейных модулей возможно создание пятикоординатного робота-станка (рис. 1). Манипулятор перемещения инструмента 1, 2, 3, 4 (рис. 1) представляет собой вращательно-линейный модуль, выполняющий перемещение по двум координатам. Шарико-винтовой преобразователь совместно с приводом (двигатель вращения гайки шарико-винтового преобразователя) осуществляет линейное перемещение вдоль оси Z_min. Перемещение инструмента вокруг оси Z_min выполняется приводом через шлицевую втулку. Манипулятор перемещения детали 5, 6, 7, 8, 9 (рис. 1) включает вращательно-линейный модуль, позволяющий выполнять перемещение детали по двум координатам: линейное перемещение детали вдоль оси Z_d и вращение вокруг оси Z_d, а также включает привод 3 вращения корпуса вращательно-линейного модуля вокруг вертикальной оси Z_Md.

В совокупности манипуляторы перемещения инструмента и детали обеспечивают обработку поверхности детали, создавая относительное перемещение детали и инструмента.

2. Решение кинематической задачи управления пятикоординатным роботом-станком. Решение кинематической задачи управления пятикоординатным роботом-станком состоит в формировании законов управления обобщенными координатами исполнительного механизма, обеспечивая перемещение режущей кромки (сопровождающий трехгранник (τνβ)_k) по заданной траектории на обрабатываемой поверхности.

В совокупности манипуляторы перемещения детали и инструмента представляют собой механизм относительного манипулирования, который позволяет осуществлять перемещение инструмента относительно обрабатываемой поверхности детали по пяти независимым координатам. Введение вычисляемых, либо задаваемых параметров, определяющих положение режущей кромки на режущей поверхности, позволяют выполнять обработку сложных поверхностей, обеспечивая положение режущей кромки инструмента по шести координатам . Входной информацией для управления обобщенными координатами обрабатывающего станка являются параметры, определяющие траекторию движения инструмента (режущей кромки) по обрабатываемой поверхности детали. Такими параметрами являются координаты сопровождающего трехгранника, связанного с формообразующей режущей кромкой инструмента при ее движении по траектории.

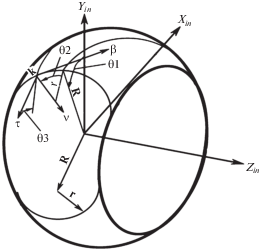
Математически для решения кинематической задачи управления обобщенными координатами исполнительного механизма станка вводится сопровождающий трехгранник (τνβ)_i, определяющий траекторию движения режущей кромки по обрабатываемой поверхности, ось τ направлена по направлению скорости движения режущей кромки, ось ν – по нормали к поверхности и β − по направлению режущей кромки (рис. 2).

Принятые направления осей координат сопровождающего трехгранника являются условными, так как режущая кромка инструмента не всегда представляет прямую линию. Однако принятое представление для описания формообразования поверхности позволяет получить зависимости между движением инструмента относительно детали и обобщенными координатами исполнительного механизма станка.

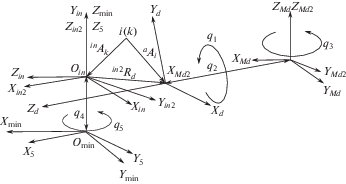
Решение кинематической задачи применительно для робота-станка на основе вращательно-линейных модулей решается введением декартовых систем координат (рис. 3): (XYZ)_Md − неподвижная система координат, связанная с манипулятором перемещения детали, принимается за нулевую систему координат, (XYZ)_min − неподвижная система координат, связанная с манипулятором инструмента, (XYZ)_Md2 − подвижная система координат, связанная с вращательно-линейным модулем манипулятора детали и перемещаемая относительно системы координат (XYZ)_Md на угол q₃, (XYZ)_d – подвижная система координат, в которой задается описание обрабатываемой поверхности детали (движение сопровождающего трехгранника (τνβ)_i) – ^dA_i(t). Данная система координат перемещается относительно системы координат (XYZ)_Md2: линейное перемещение q₂ и поворот на угол q₁.

Подвижная система координат (XYZ)_in (рис. 3) – связана с обрабатывающим инструментом, в которой задается положение режущей кромки (τνβ)_k. Система координат (τνβ)_in перемещается относительно (XYZ)_min вращательно-линейным модулем: q₄ – линейное перемещение в направлении оси Z_min и q₅ – вращение вокруг данной оси.

Для решения кинематической задачи и определения обобщенных координат механизма, обеспечивающих перемещение режущей кромки инструмента по заданной траектории на обрабатываемой поверхности детали, используются матрицы Данэвита–Хартенберга, позволяющие одновременно вычислять угловые перемещения звеньев механизма, которые связаны с соответствующей декартовой системой координат и их линейные перемещения. Элементы матриц являются функциями обобщенных координат, что позволяет получать уравнения относительно обобщенных координат, решая которые определяются зависимости между параметрами, определяющими положение режущей кромки на обрабатываемой поверхности, и обобщенными координатами.

Положение трехгранника (τνβ)_i в системе координат детали (XYZ)_d определяется матрицей

где матрица ^dC_i размерности [3 ⋅ 3] определяет направляющие косинусы осей τ, ν и β относительно осей X, Y, Z и являются функциями текущего времени t, четвертый столбец матрицы (1) ^dR_i = [x_i y_i z_i]^т определяет текущие координаты точки траектории i на обрабатываемой поверхности в системе координат (XYZ)_d.

Для определения и управления обобщенными координатами робота-станка необходимо определить точное положение координатной системы (XYZ)_min относительно (XYZ)_Md. Положение данной системы координат определяется выполнением специальной методики базирования, используя головки типа Ренешоу и специальный типовой образец детали . В качестве начала отсчета для q₅ и q₃ принимаются положения осей X_min и X_Md.

Процедура нахождения обобщенных координат выполняется последовательно, начиная с простейшего способа вычисления одной из обобщенных координат. Подставляя затем полученные значения в дальнейшие вычисления, определяются последующие недостающие обобщенные координаты.

Для удобства вычислений вводится промежуточная система координат с центром в 0_in – (XYZ)_in2, оси которой параллельны осям системы (XYZ)_Md2. Из условия равенства элементов матрицы, определяющей положения трехгранника (τνβ)_i в системе координат (XYZ)_Md, соответствующим элементам матрицы, определяющей положение режущей кромки (τνβ)_k также в системе координат (XYZ)_Md^MdA_i = ^MdA_k, составляются системы уравнений, решение которых позволяют определять обобщенные координаты робота-станка, зная параметры положения (τνβ)_i в системе координат (XYZ)_d.

Для определения обобщенной координаты q₁ и параметра θ₁ из равенства элементов матриц ^MdA_i[3, 1], ^MdA_i[3, 2], ^MdA_i[3, 3] соответствующим элементам матриц ^MdA_k[3, 1], ^MdA_k[3, 2], ^MdA_k[3, 3] составляется система уравнений

решая которую получим

Для нахождения обобщенной координаты q₃ определяются координаты вектора ⁱⁿ²R_d в системе координат (XYZ)_in2. Вектор ⁱⁿ²R_d является суммой двух векторов ⁱⁿ²R_d = = ⁱⁿ²R_k + ^kR_d.. Отношение координаты вектора ⁱⁿ²R_d на ось Y – (Y(ⁱⁿ²R_d)) системы координат (XYZ)_in2 и расстояния между центрами 0_min и 0_Md – ⁱⁿR_d = $\overline {{{0}_{{min}}}{{0}_{{Md}}}} {\text{ }}$ = L является синусом обобщенной координаты угла q₃

Из уравнения (3) после вычисления $Y{{(}^{{{\text{in2}}}}}{{R}_{{\text{d}}}})$ и преобразования получим

где

Обобщенная координата q₂ аналогично q₃ может быть определена из конструктивного расположения манипуляторов перемещения инструмента и детали

из которого

Для вычисленных q₁, q₂, q₃, θ₁ и задаваемых θ₂, θ₃ определяются обобщенные координаты q₄ и q₅. Для этого из равенства элементов матриц преобразования координат ^MdA_i [3, 4] = ^MdA_k [3, 4] составляется уравнение

из которого определяется обобщенная координата q₄

Соответственно из равенства элементов матриц ^MdA_i[1, 4] = ^MdA_k[1, 4] и ^MdA_i[2, 4] = = ^MdA_k[2, 4] составляется система уравнений

из которой определяется обобщенная координата q₅где A = (z_i + q₂)cos(q₃) + (x_i sin(q₁) + y_i cos(q₁))sin(q₃) – X_min; B = (z_i + q₂)sin(q₃) + (x_i sin(q₁) + + y_i cos(q₁))cos(q₃) – Y_min, D = rsin(θ₂), X_min и Y_min – координаты, определяющие положение точки 0_min в системе координат (XYZ)_Md.

3. Решение динамической задачи для робота-станка. Вывод динамических уравнений, определение сил и моментов в приводах и кинематических парах производится двумя способами: используя уравнения Лагранжа второго рода, что позволяет учесть все составляющие и проверить полученные выражения методом кинетостатики, позволяющим наглядно обосновать происхождение каждого слагаемого в формулах.

Для манипулятора перемещения детали

1. Момент, развиваемый приводом 1 (рис. 1)

где J_7Z – осевой момент инерции вала 7 и J_5Z – осевой момент шлицевой втулки 5 относительно оси Z_d (рис. 1).

2. Сила, развиваемая приводом 2 в направлении оси Z_d

где ${{m}_{7}}({{q}_{2}} - {{l}_{{C7}}})\dot {q}_{3}^{2}$ – центробежная сила инерции, определяемая вращением вокруг оси Z_Md; m₇ – масса вала 7; l_C7 – значение q₂, при котором центр тяжести вала 7 находится на оси привода 3.

Момент, развиваемый приводом 2 определяется по формуле

где k = $\frac{P}{{2\pi }}$; P = 0.05 м.

3. Момент, развиваемый приводом 3 вокруг оси Z_Md находим как

где ${{m}_{5}}l_{5}^{2} + {{m}_{6}}l_{6}^{2} + {{J}_{{5X}}} + {{J}_{{6X}}} + {{J}_{{7X}}} + {{J}_{{8X}}} + {{J}_{9}}$ – постоянный инерционный коэффициент, образованный центральными моментами инерции звеньев 5, 6, 7, 8 вокруг вертикальной оси и моментом инерции звена 9 вокруг оси Z_Md; ${{m}_{7}}{{({{q}_{2}} - {{l}_{{C7}}})}^{2}}$ и ${{m}_{8}}{{({{q}_{2}} - {{l}_{{C8}}})}^{2}}$ – моменты инерции сосредоточенных масс звеньев 7, 8 вокруг оси Z_Md; l_С8 – значение q₂, при котором центр тяжести винта 8 находится на оси привода 3; $2{{m}_{7}}({{q}_{2}} - {{l}_{{C7}}}){{\dot {q}}_{2}}{{\dot {q}}_{3}}$ и $2{{m}_{8}}({{q}_{2}} - {{l}_{{C8}}}){{\dot {q}}_{2}}{{\dot {q}}_{3}}$ – составляющие от моментов Кориолисовых сил; ${{\dot {q}}_{2}}$ – относительная скорость центра тяжести звена 7 и звена 8; ${{\dot {q}}_{3}}$ – угловая скорость. Угловые скорости ${{\dot {q}}_{2}}$ и ${{\dot {q}}_{3}}$ ортогональны, поэтому их удвоенное векторное произведение (ускорение Кориолиса) направлено по касательной и равно $2{{\dot {q}}_{2}}{{\dot {q}}_{3}}$. При умножении данных ускорений на соответствующие массы m₇ и m₈ получаются $2{{m}_{7}}{{\dot {q}}_{2}}{{\dot {q}}_{3}}$ и $2{{m}_{8}}{{\dot {q}}_{2}}{{\dot {q}}_{3}}$, действующие каждая на плече $({{q}_{2}} - {{l}_{{C7}}})$ – для звена 7 и $({{q}_{2}} - {{l}_{{C8}}})$ – для звена 8.

Для манипулятора перемещения инструмента

1. Сила, развиваемая приводом 4 в направлении оси Z_min

и момент, развиваемый приводом 4где q₄ – линейное перемещение, выполняемое приводом 4 в направлении оси Z_min; g – ускорение от силы тяжести звена 3.

2. Момент, развиваемый приводом 5

где J₁ – момент инерции шлицевой втулки.

Несмотря на динамическую развязку внутри модулей, имеется взаимовлияние второго и третьего привода (центробежная сила инерции влияет на второй привод, а Кориолисова сила и переменные моменты инерции от сосредоточенных масс звеньев 7, 8 влияют на третий привод).

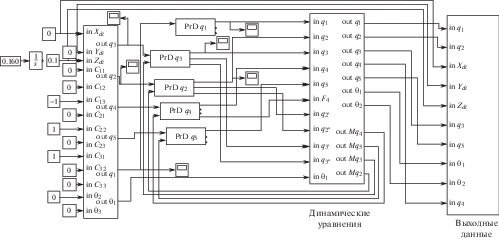
4. Динамическая модель робота-станка. Динамическая модель робота-станка, реализованная в системе MATLAB–SIMULINK приведена на рис. 4.

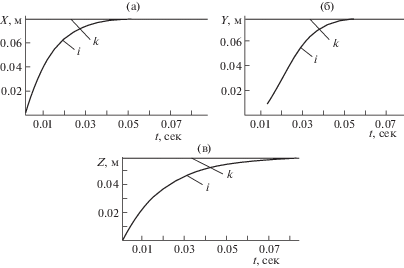
На рис. 5 приведены переходные процессы при линейном перемещении манипуляторов для совмещения i-й точки обрабатываемой поверхности с k-й точкой режущей кромки по координатам X (рис. 5a), Y (рис. 5б) и Z (рис. 5в) в системе координат (XYZ)_Md. В качестве входных сигналов принималось ступенчатое задание линейных координат трехгранника ((τνβ), x_i, y_i, z_i) в системе координат (XYZ)_d.

Заключение. Проведенные исследования применения вращательно-линейных модулей в роботах-станках позволяют сделать вывод о целесообразности использования данных модулей в конструкциях станочного оборудования, роботов, а также в механизмах, где требуется осуществлять линейные перемещения в сочетании с угловыми. Преимущество данных модулей состоит в том, что они позволяют исключить промежуточные кинематические цепи для передачи движения от исполнительного привода к выходному звену. Это повышает точность, исключив погрешности, вносимые передающими механизмами, и позволяет осуществлять прямое регулирование перемещения выходного звена, управляя непосредственно исполнительным приводом. Однако использование вращательно-линейных модулей требует учитывать взаимовлияние между приводами при выполнении перемещения по нескольким управляемым обобщенным координатам.