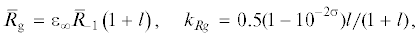Проблемы машиностроения и надежности машин, 2020, № 3, стр. 102-112

Для прогнозирования показателей надежности и долговечности технических систем в настоящее время наиболее часто применяется статистическая теория надежности. Она применима к объектам и деталям, используемым в массовом количестве в однородных условиях, где возможен сбор экспериментальных данных по причинам и интенсивностям отказов. Однако многие детали машин уникальны и дороги и изготавливаются в таком малом количестве, что не может быть речи о сборе статистических данных по их отказам. Да и условия их работы сильно отличаются. В этом случае расчет показателей надежности и долговечности должен быть выполнен на основе теоретических исследований и аналитических расчетов.

В послевоенные годы началось внедрение статистических методов в машиностроение в связи с расчетом долговечности деталей машин, работающих в условиях переменных напряжений. Существенный вклад в этом направлении сделан С.В. Серенсеном и его сотрудниками. В начале 60-х годов начинается внедрение теории случайных процессов к решению задач надежности. В машиностроении этот подход активно развивался В.В. Болотиным. В настоящее время опубликовано ряд монографий, в которых обобщены проведенные исследования в этом направлении [1–5]. Количество публикаций на эту актуальную тему в периодических изданиях и материалах научных конференций продолжает расти [6–14].

В настоящей статье в достаточно общем виде рассматривается задача расчета надежности и долговечности деталей машин по усталостному разрушению в вероятностной постановке. В результате решения задачи неявно определена монотонно убывающая во времени функция надежности H(t), которая дает надежность (вероятность неразрушения) детали по истечении определенного промежутка времени (срока службы, межремонтного периода механизма). Она также позволяет определить долговечность детали, если приравнять надежность нулю (усталостное разрушение).

Процесс накопления усталостных повреждений рассматривается на макроуровне и описывается скорректированной теорией линейного суммирования повреждений. Предельное состояние материала описывается кривой усталости.

Кривые усталости большинства материалов можно описать зависимостью

где $m$ – постоянная материала; ${{R}_{{ - 1}}}$ – предел выносливости лабораторного образца; ${{N}_{0}}$ – базовое число циклов; ${{S}_{a}}$ – амплитуда симметричного цикла напряжений; $N$ – число циклов до разрушения.

Для конкретных деталей машин вместо ${{R}_{{ - 1}}}$ используется предел выносливости детали ${{R}_{g}} = {{R}_{{ - 1}}}{\text{/}}{{K}_{{ - 1}}}$, вычисленный с учетом общего коэффициента изменения предела выносливости. При несимметричном цикле напряжений вместо ${{S}_{a}}$ используется амплитуда приведенного симметричного цикла

В связи с большим разбросом опытных данных испытанию подвергается большое количество образцов и строится полная вероятностная диаграмма. Ее можно представить в виде семейства кривых усталости в координатах $S - N$, соответствующих различной вероятности разрушения $P$ или в виде кривых распределения долговечности в координатах $P - N$, соответствующих различным напряжениям $S$. Наиболее часто применяется медианная кривая усталости и для нее в литературе приводятся постоянные материала.

Для расчетов на надежность основное значение имеет закон распределения предела выносливости. Многочисленные опытные данные свидетельствуют о том, что для этой зависимости можно принять нормальное или логарифмически нормальное распределение [1].

При расчете надежности деталей машин исключительно важны расчетные методы распространения результатов испытаний образцов на натурные детали. Такие возможности открывает статистическая теория подобия усталостного разрушения. Согласно этой теории распределение предела выносливости детали $f\left( {{{R}_{g}}} \right)$ аппроксимируется нормальным законом. При этом медианное значение ${{\overline R }_{g}}$ и коэффициент вариации ${{k}_{{Rg}}}$ предела выносливости детали определяется по формулам [1]

где $l = \frac{{1 - {{\varepsilon }_{\infty }}}}{{{{\varepsilon }_{\infty }}}}{{\left( {\frac{1}{{88.3}}\frac{L}{G}} \right)}^{{ - \nu }}}$; L – периметр зоны концентраций напряжений; G – относительный градиент напряжений.

При ориентировочных расчетах принимается $\sigma = 0.045{\kern 1pt} - {\kern 1pt} 0.05$ для конструкционных сталей и $\sigma = 0.05{\kern 1pt} - {\kern 1pt} 0.06$ – для сплавов, ${{\varepsilon }_{\infty }} = {\text{0}}{\text{.5}}$, $\nu = 0.1$.

Для расчета надежности детали по усталостному разрешению надо знать закон распределения амплитуд расчетных напряжений $f(s)$. На стадии проектирования для простых циклов его можно определить преобразованием плотностей вероятностей или решением задач статистической динамики [15, 16]. Если напряжение представляет собой гормонический процесс со случайной амплитудой или узкополосной стационарный гауссовский процесс, плотность распределения амплитуды подчиняется закону Рэлея

где $\sigma _{S}^{2}$ – дисперсия напряжения.

Характеристики нагруженности можно получить путем имитационного моделирования или путем натурных тензометрических измерений при испытаниях детали. По осциллограмме или выборке напряжений образуют массив случайных амплитуд S_i и строят гистограмму. Далее подбирается наиболее подходящий теоретический закон распределения амплитуды. Для этой цели часто используется правая ветвь нормального распределения

Если напряжение случайно не только по амплитуде, но и по коэффициенту асимметрии, то сначала производится схематизация процесса, целью которой является получение функции распределения амплитуд напряжений, эквивалентной данному случайному процессу по степени вносимого усталостного повреждения [11]. К способам схематизации относятся методы максимумов, размахов, полных циклов. Принято считать, что наиболее приемлемые результаты дает метод полных циклов. Схему реализаций этого метода и расчетные формулы можно найти в [1, 17].

Если напряжение является стационарным гауссовским процессом, то для определения плотности распределения амплитуд можно использовать выражения [17]

где ${{k}_{0}}$ – первоначальное отношение среднего числа экстремумов к среднему числу нулей.

Для определения “a” и “b” имеются два уравнения

Рассмотрим расчет надежности по усталостному разрушению при регулярной случайной загруженности. Надежность в этом случае равна вероятности непревышения случайной амплитудой детерминированной или случайной величины предела выносливости при базовом или ограниченном числе циклов. Решение таких задач в общем виде и при различных сочетаниях действующих и предельных напряжений приведено в [15]. Для нормального закона распределения предельных и действующих напряжений надежность равна

где $t = ({{n}_{N}} - 1){\text{/}}\sqrt {n_{N}^{2}k_{{{{R}_{g}}}}^{2} + k_{s}^{2}} $, ${{n}_{N}} = {{\bar {R}}_{g}}{\text{/}}{{m}_{s}}$, ${{k}_{{{{R}_{g}}}}} = {{\sigma }_{{{{R}_{g}}}}}{\text{/}}{{\bar {R}}_{g}}$; $\Phi $ – табулированная функция распределения нормального закона.

Используя выражение (1), получаем

Эти формулы позволяют рассчитать функцию распределения ресурса детали, то есть зависимость надежности от срока службы N.

Определение надежности по усталостному разрушению при случайном нагружении проведем по скорректированной гипотезе линейного суммирования повреждений, согласно которой условие усталостного разрушения за N циклов имеет вид [2, 5]

где ${{N}_{P}}\left( s \right)$ – разрушающее число циклов на уровне напряжений S; ${{a}_{P}}$ – расчетное относительное усталостное повреждение.

При случайном изменении напряжений с учетом (1) имеем

Здесь ${{S}_{m}}$ максимальное значение амплитуды, которое можно найти, задавшись вероятностью непревышения этого значения ${{H}_{{sm}}}$. Тогда ${{S}_{m}}$ определяется как корень уравнения

то есть ${{S}_{m}}$ – равна квантили распределения, соответствущей ${{H}_{{sm}}}$.

Переходя от блочного нагружения к непрерывному случайному нагружению, запишем выражение для определения расчетного повреждения

где $M = 0.5{\kern 1pt} - {\kern 1pt} 0.7$ – относительный уровень повреждающих амплитуд.

Если при расчетах по этой формуле получается ${{a}_{P}} < 0.2$, то принимаем ${{a}_{P}} = 0.2$.

Для вычисления коэффициента a введем обозначение

Запишем ${{a}_{p}} = (U - M{{x}_{0}}){\text{/}}(b - M{{x}_{0}})$, $b = {{S}_{m}}{\text{/}}{{\sigma }_{s}}$, ${{x}_{0}} = {{R}_{g}}{\text{/}}{{\sigma }_{s}}$.

Теперь из уравнения (4), приняв $a = {{a}_{P}}$, можно найти ресурс детали

где

Интегралы (6) и (8) можно вычислить, используя табулированную функцию χ²-распределения (Пирсона) – P(x, n). Для распределения Рэлея

Правая ветвь нормального распределения

В этих формулах Γ(n) – полная гамма-функция.

Из этих соотношений при ${{S}_{m}} \to \infty $ как частные случаи получаются выражения, приведенные в [1].

Для расчета надежности из уравнения (7) находим пороговое значение предела выносливости ${{R}_{ * }}$, соответствующего сроку службы в N циклов и заданному нагружению. Если фактический предел выносливости ${{R}_{g}}$ больше ${{R}_{ * }}$, то деталь не разрушится за N циклов. Следовательно, надежность детали по усталостному разрушению равна вероятности указанного события и определяется по формуле

где $\gamma = {\text{(}}{{R}_{ * }} - {{\bar {R}}_{g}}{\text{)/}}{{\sigma }_{g}}$.

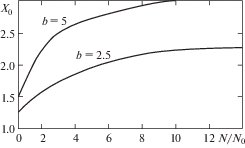
Трансцендентное уравнение (7) решается графически или на ЭВМ. Для практических расчетов полезно заранее построить график зависимости N/N₀ от х₀ для различных материалов m и нагружений $b$

Такой график для усеченного нормального закона амплитуды при $m = 9$ приведен на рис. 1.

Для определения порогового значения ${{R}_{{\text{*}}}}$ для материала деталей ($m$, ${{N}_{0}}$) при заданном нагружении ($b$, $f(S)$) и срока службы $N$ из графика находим ${{x}_{0}}$, а через него ${{R}_{{\text{*}}}} = {{x}_{0}}{{\sigma }_{S}}$. Далее по формуле (11) определяется надежность детали.

Если предел выносливости является детерминированной величиной, то из уравнения (7) или графика находим параметр b, а затем максимальное значение амплитуды S_m. Далее из уравнения (5) находим вероятность непревышения этого значения, что соответствует надежности детали.

Для расчета долговечности необходимо знать распределение числа циклов до разрушения $N$. Многочисленные испытания показали, что оно подчиняется логарифмически нормальному закону [1].

где $z = \ln N$; ${{\sigma }_{z}}$, ${{m}_{z}}$ – математическое ожидание и стандарт, определяемые экспериментально при испытаниях с постоянной амплитудой.

Вероятностные характеристики числа $N$ при этом равны

Если путем испытаний определены ${{m}_{N}}$ и ${{k}_{N}}$, то параметры распределения определяются как

Вероятность разрушения при числе циклов ${{N}_{P}}$ будет равна

Отсюда, задавшись надежностью ${{H}_{{\text{*}}}}$, можно определить долговечность детали

где ${{\gamma }_{P}}$ – квантиль нормального распределения, соответствующий вероятности $P = 1 - {{H}_{ * }}$.

Для конкретных деталей экспериментальное опредление параметров распределения (12) является очень трудоемким. В реальных условиях амплитуда напряжений имеет случайный характер. Поэтому исключительно важна разработка методов определения долговечности деталей с учетом случайных факторов.

Выражение (7), определяющее ресурс детали представим в виде $N = a{\text{/}}{\bar {v}}$, где ${\bar {v}}$ – среднее значение повреждения за один цикл

Второй момент и дисперсия единичного повреждения определяются по формулам

Число циклов до разрушения определяет долговечность детали в случае регулярного нагружения. При сложных циклах нагружения среднее значение долговечности $\bar {T}$ определяется через среднее время $\bar {t}$ между нагружениями

Дисперсия долговечности определяется по формуле [13]

где $\sigma _{t}^{2}$ – дисперсия времени между нагружениями.

Распеделение долговечности подчиняется логарифмически нормальному закону и определяется выражением (12) с заменой N на $T$.

Покажем определение показателей долговечности на примере релеевского распределения амплитуды. В этом случае по формулам (17) и (9) при больших ${{S}_{m}}$ получаем

Дисперсия единичного повреждения по (16) равна

Дисперсию долговечности найдем по формуле (18). При этом распределение времени между нагружениями считаем релеевским

Теперь

Экспериментальная проверка полученных зависимостей [2, 13] показывает, что среднее значение долговечности хорошо согласуется с опытными данными, а реальное рассеяние долговечности намного больше, чем это предсказывает последняя формула. Основная причина этого заключается в том, что при расчетах мы учитывали только случайный характер амплитуд напряжений, а механические свойства материала полагали детерминированными. Однако, предел выносливости является случайной величиной и его рассеяние оказывает существенное влияние на рассеяние долговечности.

Один из путей решения этой задачи предложен В.В. Болотиным [2] и состоит в применении формулы полной вероятности и аппроксимации условного распределения долговечности в виде дельта-функции. В результате получено распределение долговечности в виде

где $F(R)$ – функция распределения предела выносливости; ${{R}_{ * }}(t)$ – корень уравнения

Функция надежности системы определяется по формуле

При использовании формул (20) и (22) возникают трудности, связанные с определением функции ${{R}_{*}}$ из уравнения (21). Если характеристическая долговечность определяется уравнением (19), то аналитическое определение функции ${{R}_{ * }}(t)$ невозможно из-за наличия трансцендентной функции $Q(x_{0}^{2},m + 2)$. В этом случае иногда можно пользоваться приближенным решением, не учитывающим рассеяние функции $Q(x_{0}^{2},m + 2)$. Тогда

где ${{b}_{0}} = {{m}_{R}}{\text{/}}{{\sigma }_{S}};$ ${{m}_{R}}$ – математическое ожидание предела выносливости.

Пусть предел выносливости имеет двухпараметрическое распределение Вейбулла $F(R) = 1 - \exp ( - {{R}^{\beta }}{\text{/}}a)$. Тогда распределение долговечности и функцию надежности можно найти по формулам (20) и (22)

где $\alpha = \beta {\text{/}}m$, ${\text{ }}L = {{(\sqrt 2 {{\sigma }_{S}})}^{\beta }}{{[Q(b_{0}^{2},m + 2)\Gamma \left( {1 + m{\text{/}}2} \right){\text{/}}{{T}_{0}}]}^{\alpha }}{\text{/}}a$.

Из этих выражений можно найти все вероятностные характеристики долговечности. Долговечность детали с заданной надежностью ${{H}_{*}}$ будет равна $T = {{( - \ln {{H}_{*}}{\text{/}}L)}^{{m/\beta }}}$.

Математическое ожидание и коэффициент вариации долговечности

В общем случае для учета рассеяния предела выносливости применяют метод статистического моделирования. Из выражения (19) выпишем члены, зависящие от $R$: $u = {{x}^{m}}{\text{/}}Q({{x}^{2}},m + 2)$, где $x = b = R{\text{/}}{{\sigma }_{S}}$ – случайная величина.

Тогда $T = {{L}_{0}}u$, где ${{L}_{0}} = {{T}_{0}}{\text{/}}{{2}^{{m/2}}}\Gamma (1 + m{\text{/}}2)$.

Пусть для определенности предел выносливости имеет нормальное распределение. Задаемся постоянными параметрами нагружения и материала (${{\sigma }_{S}}$, ${{\sigma }_{R}}$, $m$, ${{m}_{R}}$) и генерируем величину $х$, имеющую нормальное распределение с параметрами ${{b}_{0}} = {{m}_{R}}{\text{/}}{{\sigma }_{S}}$, ${{\sigma }_{0}} = {{\sigma }_{R}}{\text{/}}{{\sigma }_{S}} = {{k}_{R}}{{b}_{0}}$.

Путем задания большого числа реализации находим значение u и после статистической обработки определяем его закон распределения. Экспериментальные данные о рассеянии долговечности [2, 17] и проведенные расчеты дают основание принять для величины $u$ логарифмически-нормальный закон распределения

где параметры распределения $с$ и $d$ находятся через моменты величины $u$ по формулам $с = 2\ln \bar {u}$ – $0.5\ln \left\langle {{{u}^{2}}} \right\rangle $, ${{d}^{2}} = \ln \left\langle {{{u}^{2}}} \right\rangle $ – $2\ln \bar {u}$.

Через моменты величины $u$ находим и моменты долговечности

Преобразованием плотности вероятности $P(u)$ находим распределение долговечности

Определение гамма-процентного ресурса производится по формуле (15)

Аналитическое решение задачи можно получить, если пренебречь рассеянием функции $Q(b_{0}^{2},m + 2)$. Вероятностные характеристики долговечности тогда будут вычисляться по формулам

где $\bar {y} = b_{0}^{m}[1 + m(m - 1)k_{R}^{2}{\text{/}}2]$.

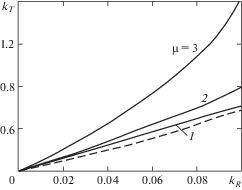
На рис. 2 показан график зависимости коэффициента вариации долговечности от коэффициента вариации предела выносливости при различных ${{b}_{0}}$ для $m = 6$ (1, при ${{b}_{0}} = 1$; 2, при ${{b}_{0}} = 2$; 3, при ${{b}_{0}} = 3$).

Там же пунктирными линиями показана эта же зависимость без учета рассеяния функции $Q(b_{0}^{2},m + 2).$ Важно отметить, что в этом случае ${{k}_{T}}$ не зависит от ${{b}_{0}}$. Такой же характер имеют кривые и при других m, хотя коэффициент вариации ${{k}_{T}}$ увеличивается с ростом $m$.

Если в детали возникает плоское напряженное состояние с амплитудами нормальных ${{S}_{\sigma }}$ и касательных ${{S}_{\tau }}$ напряжений, являющихся случайными функциями, то расчет долговечности производится с применением одного из критериев разрушения. Чаще всего используется эллиптическая зависимость, выраженная через эквивалентные напряжения S_σe, S_τe

Эквивалентное напряжение найдем из условия равенства ${\bar {v}}$ единичному повреждению от эквивалентного напряжения

Отсюда находим ${{S}_{{\sigma e}}} = I_{\sigma }^{{1/{{m}_{\sigma }}}}$, ${{S}_{{\tau e}}} = I_{\tau }^{{1/{{m}_{\tau }}}}$, где ${{m}_{\sigma }}$, ${{m}_{\tau }}$ – показатели кривой усталости при испытаниях по нормальным и касательным напряжениям.

Если на деталь действуют только нормальные напряжения, то ее долговечность можно определить по формуле (7) и соответствующий ей предел выносливости равен ${{R}_{{g\sigma }}}$ = ${{({{N}_{\sigma }}{{I}_{\sigma }}{\text{/}}{{a}_{\sigma }}{{N}_{{0\sigma }}})}^{{1/{{m}_{\sigma }}}}}$.

Число циклов до разрушения в общем случае нагружения $N = {{a}_{\sigma }}{{N}_{{0\sigma }}}$ = ${{a}_{\tau }}{{N}_{{0\tau }}}$ находим ${{S}_{{\sigma e}}}{\text{/}}{{R}_{{g\sigma }}}$ = ${{(N{\text{/}}{{N}_{\sigma }})}^{{1/{{m}_{\sigma }}}}}$. Тогда критерий разрушения примет вид

Для многих материалов ${{m}_{\sigma }} = {{m}_{\tau }} = m$. Тогда из (27) имеем

Плотность распределения долговечности определяется выражением (12). Чтобы найти параметры распределения, введем обозначения $z = \ln N$, ${{z}_{1}} = \ln {{N}_{\sigma }}$, ${{z}_{2}} = \ln {{N}_{\tau }}$ и прологарифмируем выражение (28)

Отсюда находим математическое ожидание

Дисперсию $z$ находим по приближенной формуле

где ${{d}_{1}} = {{\left( {\frac{{\partial z}}{{\partial {{z}_{1}}}}} \right)}_{m}} = 1 - \frac{1}{{1 + {{{({{{\bar {N}}}_{\tau }}{\text{/}}{{{\bar {N}}}_{\sigma }})}}^{{2/m}}}}}$; ${{d}_{2}} = {{\left( {\frac{{\partial z}}{{\partial {{z}_{2}}}}} \right)}_{m}}$ = $1 - \frac{1}{{1 + {{{({{{\bar {N}}}_{\sigma }}{\text{/}}{{{\bar {N}}}_{\tau }})}}^{{2/m}}}}}$.

В этих формулах ${{m}_{{z1}}}$, ${{m}_{{z2}}}$, $\sigma _{{z1}}^{2}$, $\sigma _{{z2}}^{2}$ определяются экспериментально. При этом ${{\bar {N}}_{\sigma }}$, ${{\bar {N}}_{\tau }}$ определяются по формуле (13). Если экспериментально определены вероятностные характеристики ${{\bar {N}}_{\sigma }}$, ${{\bar {N}}_{\tau }}$, ${{\sigma }_{{N\sigma }}}$, ${{\sigma }_{{N\tau }}}$, то параметры распределения нормальных и касательных напряжений определяются по формуле (14).

После определения параметров распределения гамма-процентный ресурс деталей определяются по формуле (15).

Таким образом, в статье получены следующие новые научные результаты: 1. На основе статистических закономерностей усталостного разрушения получены формулы для расчета надежности деталей машин по усталостному разрушению, когда расчетные и предельные напряжения представляют собой случайные величины с известными законами распределения. 2. На основе скорректированной теории линейного суммирования повреждений получены соотношения для расчета долговечности деталей машин при случайных воздействиях с учетом рассеяния предела выносливости. 3. Предложена методика расчета долговечности при случайном изменении компонент плоского напряженного состояния.