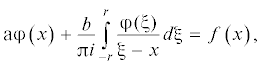Проблемы машиностроения и надежности машин, 2020, № 3, стр. 45-55

К ВОПРОСУ О КОНЦЕНТРАЦИИ НАПРЯЖЕНИЙ И ОПТИМИЗАЦИИ ФОРМЫ ПЕРЕХОДНОЙ ПОВЕРХНОСТИ СТУПЕНЧАТОГО ВАЛА

М. Н. Ерохин^1, *, П. В. Дородов², А. С. Дорохов³

¹ Российский государственный аграрный университет – МСХА им. К.А. Тимирязева
Москва, Россия

² Ижевская государственная сельскохозяйственная академия
Ижевск, Россия

³ Федеральный научный агроинженерный центр ВИМ
Москва, Россия

^* E-mail: sibirev2011@yandex.ru

Поступила в редакцию 21.10.2019
Принята к публикации 31.01.2020

DOI: 10.31857/S0235711920030050

Полный текст (PDF)

Аннотация

В статье представлено аналитическое решение прямой краевой и плоской задачи о напряженном состоянии в срединной поверхности ступенчатого вала. В краевой задаче применяется сингулярное интегральное уравнение с ядром Коши, решение которого находится в виде неограниченного возрастания напряжений на концах интервала интегрирования. Плоская задача представлена в тригонометрических рядах, где постоянные коэффициенты определены из краевых условий, которые предварительно разложены в ряды Фурье. Сравнение полученных результатов с научными источниками и экспериментальные исследования напряженного состояния при помощи лазерного полярископа на плоских прозрачных моделях ступенчатых деталей с галтелями постоянной и переменной кривизны подтвердили адекватность представленного решения.

Ключевые слова: ступенчатый вал, концентрация напряжений, галтель, переходная поверхность, оптимизация формы

Целью исследований является разработка методики расчета оптимальной формы переходной поверхности ступенчатого вала.

Анализ современного состояния рассматриваемой проблемы. Проблемам определения напряжений в местах различных концентраторов с заданной геометрической формой (прямая задача) посвящена обширная область теории упругости и механики деформируемого твердого тела. Концентрация напряжений численно характеризуется коэффициентами концентрации, однако точные аналитические решения для их определения найдены только в некоторых задачах. В последнее время в связи с широким применением математических пакетов программ и численных методов в задачах теории упругости оказывается возможным найти теоретические коэффициенты концентрации напряжений с достаточной для практических целей точностью. Эти коэффициенты в упругой зоне нагружения для различных типов конструктивных элементов приведены в справочниках по концентрации напряжений, нормах, технических условиях на проектирование конструкций и в других аналогичных источниках. В иных задачах, не имеющих даже численного решения, для определения коэффициентов концентрации и закона распределения напряжений применяются экспериментальные методы: фотоупругости, голографической интерферометрии, тензометрии, муаровых полос и др. Но все экспериментальные методы отличаются большой трудоемкостью или высокой стоимостью лабораторного оборудования.

Отыскание оптимальных геометрических форм деталей при их проектировании (обратная задача), когда известно или задается напряженное состояние, встречается с серьезными математическими трудностями. В ряде случаев подобное проектирование оптимальной формы сводится к решению вариационных задач с неизвестными границами, для которых отсутствуют регулярные методы исследования. Известные трудности связаны также с тем, что задачи оптимизации формы упругих тел относятся к числу нелинейных задач механики [1–5].

Разработка методов оптимизации формы деталей конструкций машин, несущих основную нагрузку, имеет важное прикладное и теоретическое значение в решении задач повышения их надежности и в значительной степени активизирует развитие машинных технологий на производстве.

Обоснование актуальности рассматриваемой проблемы. Валы в любом механизме или машине принадлежат к числу наиболее ответственных деталей, выход из строя которых обычно представляет собой угрозу для всего привода. Часто валы имеют ступенчатую форму, разрушение которых связано с возникновением усталостных трещин в местах перехода от меньшего сечения к большему. Для снижения концентрации напряжений переходные поверхности скругляют галтелями постоянной или переменной кривизны, однако остается актуальным вопрос об их оптимальной форме [1, 2].

Задача исследований. Разработка методики расчета оптимальной формы переходной поверхности ступенчатого вала в условиях сложного сопротивления.

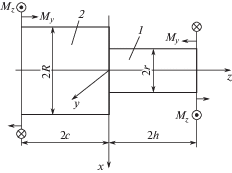
Методика исследований. Рассмотрим расчетную схему элемента ступенчатого вала при изгибе с кручением (рис. 1).

Рис. 1.

Элемент ступенчатого вала при изгибе с кручением.

Проведем последовательный расчет ступенчатого вала, применяя для жесткого изотропного материала принцип независимости действия силовых факторов (суперпозиции). Вначале решим прямую задачу для элемента вала с концентрацией напряжений (без галтели). Для определения напряжений на линии сопряжения ступени 1 и основания 2 (|x| ≤ r; z = 0) воспользуемся особым интегральным уравнением [6–11]

(1)

где при чистом изгибе примем

${\varphi }\left( x \right) = {{{\sigma }}_{z}}\left( {x;0} \right) = {{{\sigma }}_{{z{\text{м}}}}},$

$f\left( x \right) = - i\frac{{d{{w}_{{\text{м}}}}}}{{dx}},$

при чистом кручении

${\varphi }\left( x \right) = {\tau }\left( {x;0} \right) = {{{\tau }}_{{\text{м}}}},$

$f\left( x \right) = - i\frac{{d{{{v}}_{{\text{м}}}}}}{{dx}}.$

Здесь σ_zм, τ_м – местные нормальные и касательные напряжения на линии сопряжения; w_м, ${v}$_м – местные перемещения на линии сопряжения; a, b – упругие постоянные.

Решение уравнения (1), в случае неограниченного возрастания напряжений на концах линии сопряжения, имеет вид [6, 7]

(2)

${\varphi }\left( x \right) = - \frac{A}{{{\pi }i}}\frac{1}{{\sqrt {{{r}^{2}} - {{x}^{2}}} }}\mathop \smallint \limits_{ - r}^{ + r} \frac{{\sqrt {{{r}^{2}} - {{{\xi }}^{2}}} f\left( {\xi } \right)}}{{{\xi } - x}}d{\xi } + \frac{B}{{{\pi }\sqrt {{{r}^{2}} - {{x}^{2}}} }},$

где A, B – постоянные, зависящие от упругих свойств и внешней нагрузки.

Примем

$\left. {\begin{array}{*{20}{c}} {{{w}_{{\text{м}}}} = \theta x,} \\ {{{{v}}_{{\text{м}}}} = \alpha x,} \end{array}} \right\}$

где θ, α – углы наклона и поворота линии сопряжения.

Тогда из (2) получаем [7]

$\left. {\begin{array}{*{20}{c}} {{{\sigma }_{{z{\text{м}}}}} = - \frac{{{{A}_{1}}{\theta }x}}{{\sqrt {{{r}^{2}} - {{x}^{2}}} }} + \frac{{{{B}_{1}}}}{{{\pi }\sqrt {{{r}^{2}} - {{x}^{2}}} }},} \\ {{{\tau }_{{\text{м}}}} = - \frac{{{{A}_{2}}\alpha x}}{{\sqrt {{{r}^{2}} - {{x}^{2}}} }} + \frac{{{{B}_{2}}}}{{{\pi }\sqrt {{{r}^{2}} - {{x}^{2}}} }}.} \end{array}} \right\}$

Для определения постоянных воспользуемся условиями равновесия

$\left. {\begin{array}{*{20}{c}} {\mathop \smallint \limits_{ - r}^r {{{\sigma }}_{{z{\text{м}}}}}dx = 0,} \\ {\mathop \smallint \limits_{ - r}^r {{{\tau }}_{{\text{м}}}}dx = 0,} \end{array}} \right\}$

откуда B₁ = B₂ = 0;

$\left. {\begin{array}{*{20}{c}} {\mathop \smallint \limits_{ - r}^r {{{\sigma }}_{{z{\text{м}}}}}xdx = \frac{{8{{M}_{y}}}}{{3{\pi }r}},} \\ {\mathop \smallint \limits_{ - r}^r {{{\tau }}_{{\text{м}}}}xdx = \frac{{4{{M}_{z}}}}{{3{\pi }r}},} \end{array}} \right\}$

откуда

$\left. {\begin{array}{*{20}{c}} {{{A}_{1}}\theta = - \frac{{16{{M}_{y}}}}{{3{{\pi }^{2}}{{r}^{3}}}},} \\ {{{A}_{2}}\alpha = - \frac{{8{{M}_{z}}}}{{3{{{\pi }}^{2}}{{r}^{3}}}},} \end{array}} \right\}~$

где M_y, M_z – изгибающий и крутящий моменты соответственно.

Окончательно местные напряжения на линии сопряжения примут вид

(3)

$\left. {\begin{array}{*{20}{c}} {{{{\sigma }}_{{z{\text{м}}}}} = \frac{{16{{M}_{y}}}}{{3{{{\pi }}^{2}}{{r}^{3}}}}\frac{x}{{\sqrt {{{r}^{2}} - {{x}^{2}}} }},} \\ {{{\sigma }_{{x0}}} = 0,} \\ {{{{\tau }}_{{\text{м}}}} = \frac{{8{\beta }{{M}_{y}}}}{{3{{{\pi }}^{2}}{{r}^{3}}}}\frac{x}{{\sqrt {{{r}^{2}} - {{x}^{2}}} }},} \end{array}} \right\}$

где β = M_z/M_y.

Функции (3), а также нормальные и касательные напряжения для крайнего правого сечения

$\left. {\begin{array}{*{20}{c}} {\sigma = \frac{{4{{M}_{y}}}}{{{\pi }{{r}^{4}}}}x,} \\ {\tau = \frac{{2{{M}_{z}}}}{{{\pi }{{r}^{4}}}}x = \frac{{2{\beta }{{M}_{y}}}}{{{\pi }{{r}^{4}}}}x} \end{array}} \right\}~~$

и для крайнего левого сечения вала

$\left. {\begin{array}{*{20}{c}} {\sigma = \frac{{4{{M}_{y}}}}{{{\pi }{{R}^{4}}}}x,} \\ {\tau = \frac{{2{{M}_{z}}}}{{{\pi }{{R}^{4}}}}x = \frac{{2{\beta }{{M}_{y}}}}{{{\pi }{{R}^{4}}}}x} \end{array}} \right\}~~$

раскладываем в ряды Фурье

$\left. \begin{gathered} {{\sigma }_{{z{\text{м}}}}} = {{A}_{0}} + \mathop \sum \limits_{n = 1}^\infty \left( {{{A}_{n}}\cos \left( {\lambda x} \right) + {{A}_{{n1}}}\sin \left( {\lambda x} \right)} \right), \\ {{\tau }_{{\text{м}}}} = {{B}_{0}} + \mathop \sum \limits_{n = 1}^\infty \left( {{{B}_{n}}\sin \left( {\lambda x} \right) + {{B}_{{n1}}}\cos \left( {\lambda x} \right)} \right), \\ \sigma = B_{0}^{{\text{*}}} + \mathop \sum \limits_{n = 1}^\infty (B_{n}^{*}\cos \left( {\lambda x} \right) + B_{{n1}}^{*}\sin \left( {\lambda x} \right)), \\ \tau = {{D}_{0}} + \mathop \sum \limits_{n = 1}^\infty \left( {{{D}_{n}}\sin \left( {\lambda x} \right) + {{D}_{{n1}}}\cos \left( {\lambda x} \right)} \right). \\ \end{gathered} \right\}$

Здесь для левой части вала 2 (основания) при λ = nπ/R свободные члены и коэффициенты рядов запишутся

${{A}_{{n1}}} = \frac{{16{{M}_{y}}}}{{3{{{\pi }}^{2}}{{r}^{3}}R}}{{I}_{{n1}}}\left( {{\lambda }r} \right),\quad {{B}_{n}} = \frac{{8{\beta }{{M}_{y}}}}{{3{{{\pi }}^{2}}{{r}^{3}}R}}{{I}_{{n1}}}\left( {{\lambda }r} \right),$

${{A}_{0}} = {{A}_{n}} = {{B}_{0}} = {{B}_{{n1}}} = B_{0}^{*} = B_{n}^{*} = {{D}_{0}} = {{D}_{{n1}}} = 0,$

$B_{{n1}}^{*} = \frac{{8{{M}_{y}}}}{{\pi {{\lambda }^{2}}{{R}^{5}}}}\left( {\sin \left( {n\pi } \right) - \left( {n\pi } \right)\cos ~\left( {n\pi } \right)} \right),$

${{D}_{n}} = \frac{{4\beta {{M}_{y}}}}{{\pi {{\lambda }^{2}}{{R}^{5}}}}\left( {\sin \left( {n\pi } \right) - \left( {n\pi } \right)\cos ~\left( {n\pi } \right)} \right),$

где ${{I}_{{n1}}} = \int_{ - r}^r {\frac{x}{{\sqrt {{{r}^{2}} - {{x}^{2}}} }}\sin \left( {\lambda x} \right)dx} .$

Для правой части вала 1 (ступени) в вышеприведенных формулах необходимо R заменить на r. Записываем напряжения σ_z(x, z), σ_x(x, z), τ_xz(x, z) для срединной плоскости xz вала в тригонометрических рядах с постоянными коэффициентами C_in [7, 11]

${{\sigma }_{z}} = {{\sigma }_{{z0}}} - \mathop \sum \limits_{n = 1}^\infty \,{{\lambda }^{2}}\left( {\left( {{{C}_{{1n}}}\operatorname{ch} \left( {\lambda z} \right) + {{C}_{{2n}}}\operatorname{sh} \left( {\lambda z} \right) + {{C}_{{3n}}}z\operatorname{ch} \left( {\lambda z} \right) + } \right.} \right.$

$ + \;\left. {{{C}_{{4n}}}z\operatorname{sh} \left( {\lambda z} \right)} \right)\cos \left( {\lambda x} \right) + \left( {{{C}_{{5n}}}\operatorname{ch} \left( {\lambda z} \right) + {{C}_{{6n}}}\operatorname{sh} \left( {\lambda z} \right) + } \right.$

$\left. { + \;{{C}_{{7n}}}z\operatorname{ch} \left( {\lambda z} \right) + \left. {{{C}_{{8n}}}z\operatorname{sh} \left( {\lambda z} \right)} \right)\sin \left( {\lambda x} \right)} \right);$

${{\sigma }_{x}} = {{\sigma }_{{x0}}} + \mathop \sum \limits_{n = 1}^\infty \left( {\left( {{{C}_{{1n}}}} \right.} \right.{{\lambda }^{2}}\operatorname{ch} \left( {\lambda z} \right) + {{C}_{{2n}}}{{\lambda }^{2}}\operatorname{sh} \left( {\lambda z} \right) + {{C}_{{3n}}}\lambda \left( {2\operatorname{sh} \left( {\lambda z} \right) + \lambda z\operatorname{ch} \left( {\lambda z} \right)} \right) + $

$ + \;\left. {{{C}_{{4n}}}\lambda \left( {2\operatorname{ch} \left( {\lambda z} \right) + \lambda z\operatorname{sh} \left( {\lambda z} \right)} \right)} \right)\cos \left( {\lambda x} \right) + \left( {{{C}_{{5n}}}} \right.{{\lambda }^{2}}\operatorname{ch} \left( {\lambda z} \right) + {{C}_{{6n}}}{{\lambda }^{2}}\operatorname{sh} \left( {\lambda z} \right) + $

$ + \;\left. {{{C}_{{7n}}}\lambda \left( {2\operatorname{sh} \left( {\lambda z} \right) + \lambda z\operatorname{ch} \left( {\lambda z} \right)} \right) + \left. {{{C}_{{8n}}}\lambda \left( {2\operatorname{ch} \left( {\lambda z} \right) + \lambda z\operatorname{sh} \left( {\lambda z} \right)} \right)} \right)\sin \left( {\lambda x} \right)} \right);$

${{\tau }_{{xz}}} = {{\tau }_{{xz0}}} + \mathop \sum \limits_{n = 1}^\infty \,\lambda \left( {\left( {{{C}_{{1n}}}\lambda \operatorname{sh} \left( {\lambda z} \right) + {{C}_{{2n}}}\lambda \operatorname{ch} \left( {\lambda z} \right) + {{C}_{{3n}}}\left( {\operatorname{ch} \left( {\lambda z} \right) + \lambda z\operatorname{sh} \left( {\lambda z} \right)} \right) + } \right.} \right.$

$ + \;\left. {{{C}_{{4n}}}\left( {\operatorname{sh} \left( {\lambda z} \right) + \lambda z\operatorname{ch} \left( {\lambda z} \right)} \right)} \right)\sin \left( {\lambda x} \right) - \left( {{{C}_{{5n}}}\lambda \operatorname{sh} \left( {\lambda z} \right) + {{C}_{{6n}}}\lambda \operatorname{ch} \left( {\lambda z} \right) + } \right.$

$ + \;\left. {{{C}_{{7n}}}\left( {\operatorname{ch} \left( {\lambda z} \right) + \lambda z\operatorname{sh} \left( {\lambda z} \right)} \right) + \left. {{{C}_{{8n}}}\left( {\operatorname{sh} \left( {\lambda z} \right) + \lambda z\operatorname{ch} \left( {\lambda z} \right)} \right)} \right)\cos \left( {\lambda x} \right)} \right).$

Для левой части 2 (основания) вала с граничными условиями

$\left. {\begin{array}{*{20}{l}} {{\text{1)}}\;{{{\left. {{{\sigma }_{z}}} \right|}}_{{z = + c}}} = {{\sigma }_{{z{\text{м}}}}},\quad ~\left( {\left| x \right| \leqslant r} \right),} \\ {2)\;~{{{\left. {{{\tau }_{{xz}}}} \right|}}_{{z = + c}}} = {{\tau }_{{\text{м}}}},\quad ~\left( {\left| x \right| \leqslant r} \right),} \\ {3)\;~{{{\left. {{{\sigma }_{z}}} \right|}}_{{z = - c}}} = \frac{{4{{M}_{y}}}}{{\pi {{R}^{4}}}}x,\quad ~\left( {\left| x \right| \leqslant R} \right),} \\ {4)\;~{{{\left. {{{\tau }_{{xz}}}} \right|}}_{{z = - c}}} = \frac{{2{{M}_{z}}}}{{\pi {{R}^{4}}}}x,~\quad \left( {\left| x \right| \leqslant R} \right)} \end{array}} \right\}$

и началом координат в точке (0; –с) постоянные C_in, а также свободные члены рядов определяем по формулам [7, 11]

${{C}_{{1n}}} = - \frac{{({{A}_{n}} + B_{n}^{*})\left( {\operatorname{sh} \left( {\lambda c} \right) + \lambda c\operatorname{ch} \left( {\lambda c} \right)} \right) + \left( {{{B}_{n}} - {{D}_{n}}} \right)\lambda c\operatorname{sh} \left( {\lambda c} \right)}}{{{{\lambda }^{2}}\left( {\operatorname{sh} \left( {2\lambda c} \right) + 2\lambda c} \right)}},$

${{C}_{{2n}}} = - \frac{{({{A}_{n}} - B_{n}^{*})\left( {\operatorname{ch} \left( {\lambda c} \right) + \lambda c\operatorname{sh} \left( {\lambda c} \right)} \right) + \left( {{{B}_{n}} + {{D}_{n}}} \right)\lambda c\operatorname{ch} \left( {\lambda c} \right)}}{{{{\lambda }^{2}}\left( {\operatorname{sh} \left( {2\lambda c} \right) - 2\lambda c} \right)}},$

${{C}_{{3n}}} = \frac{{({{A}_{n}} - B_{n}^{*})\operatorname{ch} \left( {\lambda c} \right) + \left( {{{B}_{n}} + {{D}_{n}}} \right)\operatorname{sh} \left( {\lambda c} \right)}}{{\lambda \left( {\operatorname{sh} \left( {2\lambda c} \right) - 2\lambda c} \right)}},$

${{C}_{{4n}}} = \frac{{({{A}_{n}} - B_{n}^{*})\operatorname{sh} \left( {\lambda c} \right) + \left( {{{B}_{n}} - {{D}_{n}}} \right)\operatorname{ch} \left( {\lambda c} \right)}}{{\lambda \left( {\operatorname{sh} \left( {2\lambda c} \right) + 2\lambda c} \right)}},$

${{C}_{{5n}}} = - \frac{{({{A}_{{n1}}} - B_{{n1}}^{*})\left( {\operatorname{sh} \left( {\lambda c} \right) + \lambda c\operatorname{ch} \left( {\lambda c} \right)} \right) - \left( {{{B}_{{n1}}} - {{D}_{{n1}}}} \right)\lambda c\operatorname{sh} \left( {\lambda c} \right)}}{{{{\lambda }^{2}}\left( {\operatorname{sh} \left( {2\lambda c} \right) + 2\lambda c} \right)}},$

${{C}_{{6n}}} = - \frac{{({{A}_{{n1}}} - B_{{n1}}^{*})\left( {\operatorname{ch} \left( {\lambda c} \right) + \lambda c\operatorname{sh} \left( {\lambda c} \right)} \right) - \left( {{{B}_{{n1}}} + {{D}_{{n1}}}} \right)\lambda c\operatorname{ch} \left( {\lambda c} \right)}}{{{{\lambda }^{2}}\left( {\operatorname{sh} \left( {2\lambda c} \right) - 2\lambda c} \right)}},$

${{C}_{{7n}}} = \frac{{({{A}_{{n1}}} - B_{{n1}}^{*})\operatorname{ch} \left( {\lambda c} \right) - \left( {{{B}_{{n1}}} + {{D}_{{n1}}}} \right)\operatorname{sh} \left( {\lambda c} \right)}}{{\lambda \left( {\operatorname{sh} \left( {2\lambda c} \right) - 2\lambda c} \right)}},$

${{C}_{{8n}}} = \frac{{({{A}_{{n1}}} - B_{{n1}}^{*})\operatorname{sh} \left( {\lambda c} \right) - \left( {{{B}_{{n1}}} - {{D}_{{n1}}}} \right)\operatorname{ch} \left( {\lambda c} \right)}}{{\lambda \left( {\operatorname{sh} \left( {2\lambda c} \right) + 2\lambda c} \right)}},$

${{\sigma }_{{z0}}} = {{A}_{0}},\quad {{\sigma }_{{x0}}} = A_{0}^{*},\quad {{\tau }_{{xz0}}} = {{B}_{0}}.$

Для правой части 1 (ступени) вала с граничными условиями

$\left. {\begin{array}{*{20}{l}} {{\text{1)}}\;{{{\left. {{{\sigma }_{z}}} \right|}}_{{z = + h}}} = \frac{{4{{M}_{y}}}}{{\pi {{r}^{4}}}}x,~} \\ {2)\;~{{{\left. {{{\tau }_{{xz}}}} \right|}}_{{z = + h}}} = \frac{{2{{M}_{z}}}}{{\pi {{r}^{4}}}}x,~} \\ {3)\;~{{{\left. {{{\sigma }_{z}}} \right|}}_{{z = - h}}} = {{\sigma }_{{z{\text{м}}}}},} \\ {4)\;~{{{\left. {{{\tau }_{{xz}}}} \right|}}_{{z = - h}}} = {{\tau }_{{\text{м}}}},} \\ {\;\;\;\;\;\left( {\left| x \right| \leqslant r} \right)} \end{array}} \right\}$

и началом координат в точке (0; +h) постоянные C_in, а также свободные члены рядов определяем по формулам [7, 11]

${{C}_{{1n}}} = - \frac{{({{A}_{n}} - B_{n}^{*})\left( {\operatorname{sh} \left( {\lambda h} \right) + \lambda h\operatorname{ch} \left( {\lambda h} \right)} \right) - \left( {{{B}_{n}} - {{D}_{n}}} \right)\lambda h\operatorname{sh} \left( {\lambda h} \right)}}{{{{\lambda }^{2}}\left( {\operatorname{sh} \left( {2\lambda h} \right) + 2\lambda h} \right)}},$

${{C}_{{2n}}} = \frac{{({{A}_{n}} - B_{n}^{*})\left( {\operatorname{ch} \left( {\lambda h} \right) + \lambda h\operatorname{sh} \left( {\lambda h} \right)} \right) - \left( {{{B}_{n}} + {{D}_{n}}} \right)\lambda h\operatorname{ch} \left( {\lambda h} \right)}}{{{{\lambda }^{2}}\left( {\operatorname{sh} \left( {2\lambda h} \right) - 2\lambda h} \right)}},$

${{C}_{{3n}}} = - \frac{{({{A}_{n}} - B_{n}^{*})\operatorname{ch} \left( {{\lambda }h} \right) - \left( {{{B}_{n}} + {{D}_{n}}} \right)\operatorname{sh} \left( {{\lambda }h} \right)}}{{{\lambda }\left( {\operatorname{sh} \left( {2{\lambda }h} \right) - 2{\lambda }h} \right)}},$

${{C}_{{4n}}} = \frac{{({{A}_{n}} - B_{n}^{*})\operatorname{sh} \left( {\lambda h} \right) - \left( {{{B}_{n}} - {{D}_{n}}} \right)\operatorname{ch} \left( {\lambda h} \right)}}{{\lambda \left( {\operatorname{sh} \left( {2\lambda h} \right) + 2\lambda h} \right)}},$

${{C}_{{5n}}} = - \frac{{({{A}_{{n1}}} - B_{{n1}}^{*})\left( {\operatorname{sh} \left( {\lambda h} \right) + \lambda h\operatorname{ch} \left( {\lambda c} \right)} \right) + \left( {{{B}_{{n1}}} - {{D}_{{n1}}}} \right)\lambda h\operatorname{sh} \left( {\lambda h} \right)}}{{{{\lambda }^{2}}\left( {\operatorname{sh} \left( {2\lambda h} \right) + 2\lambda h} \right)}},$

${{C}_{{6n}}} = \frac{{({{A}_{{n1}}} - B_{{n1}}^{*})\left( {\operatorname{ch} \left( {\lambda h} \right) + \lambda h\operatorname{sh} \left( {\lambda h} \right)} \right) + \left( {{{B}_{{n1}}} + {{D}_{{n1}}}} \right)\lambda h\operatorname{ch} \left( {\lambda h} \right)}}{{{{\lambda }^{2}}\left( {\operatorname{sh} \left( {2\lambda h} \right) - 2\lambda h} \right)}},$

${{C}_{{7n}}} = - \frac{{({{A}_{{n1}}} - B_{{n1}}^{*})\operatorname{ch} \left( {\lambda h} \right) + \left( {{{B}_{{n1}}} + {{D}_{{n1}}}} \right)\operatorname{sh} \left( {\lambda h} \right)}}{{\lambda \left( {\operatorname{sh} \left( {2\lambda h} \right) - 2\lambda h} \right)}},$

${{C}_{{8n}}} = \frac{{({{A}_{{n1}}} - B_{{n1}}^{*})\operatorname{sh} \left( {\lambda h} \right) + \left( {{{B}_{{n1}}} - {{D}_{{n1}}}} \right)\operatorname{ch} \left( {\lambda h} \right)}}{{\lambda \left( {\operatorname{sh} \left( {2\lambda h} \right) + 2\lambda h} \right)}},$

${{\sigma }_{{z0}}} = {{A}_{0}},\quad {{\sigma }_{{x0}}} = A_{0}^{*},\quad {{\tau }_{{xz0}}} = {{B}_{0}}.$

По известной формуле

${{\tau }_{{\max }}} = \sqrt {{{{\left( {\frac{{{{\sigma }_{x}} - {{\sigma }_{z}}}}{2}} \right)}}^{2}} + \tau _{{xz}}^{2}} $

определяем максимальные касательные напряжения и приводим их к безразмерным величинам согласно выражениям (4) и (5)

(4)

$s\left( {x{\text{/}}t;z{\text{/}}t} \right) = \frac{{{{{\tau }}_{{{\text{max}}}}}}}{{{{{\sigma }}_{{\text{н}}}}}},$

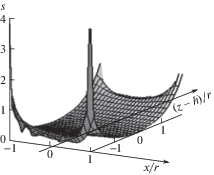
где за эквивалентные номинальные напряжения примем

(5)

${{{\sigma }}_{{\text{н}}}} = \frac{{16{{M}_{y}}}}{{3{{{\pi }}^{2}}{{r}^{3}}}}\sqrt {1 + {{{\beta }}^{2}}} .$

На рис. 2 представлена эпюра максимальных касательных напряжений в безразмерных величинах при R = c = h = 2r и β = 1 для ступени вала.

Рис. 2.

Эпюра максимальных касательных напряжений в безразмерных величинах для ступени вала.

Исследование концентрации напряжений в ступенчатых деталях с плоской срединной поверхностью и постоянным радиусом скругления галтели представлено в [11]. Если за эквивалентные номинальные напряжения принять (5), то теоретический коэффициент концентрации α_Т по наибольшим эквивалентным напряжениям

$\sqrt {\sigma _{{z0}}^{2} + 4\tau _{0}^{2}} = \frac{{16{{M}_{y}}}}{{3{{\pi }^{3}}{{r}^{3}}}}\sqrt {1 + {{\beta }^{2}}} \frac{x}{{\sqrt {{{r}^{2}} - {{x}^{2}}} }},$

при $x \to r$ и условии ограниченности напряжений в галтелях вала, запишется

(6)

${{\alpha }_{T}} = \mathop {\lim }\limits_{x \to r} \left( {\frac{{\sqrt {\sigma _{{z0}}^{2} + 4\tau _{0}^{2}} }}{{{{\sigma }_{{\text{н}}}}}}} \right) = \frac{1}{{\sqrt {1 - {{{\left( {\frac{r}{{{{r}_{0}}}}} \right)}}^{2}}} }},$

где r₀ – радиус ступени вала без галтели (r₀ > r). Тогда, воспользовавшись выводами в [11] и выражением (6), получим уравнение

(7)

$\frac{{\alpha _{T}^{2}}}{{\alpha _{T}^{2} - 1}} - \frac{{{{{\left( {{{\alpha }_{T}} - 1} \right)}}^{2}}\rho _{0}^{2}}}{2} - 2\left( {2\sqrt 2 - 1} \right)\rho _{0}^{2} - 2\sqrt 2 {{\rho }_{0}} - 1 = 0,$

где ${{{\rho }}_{0}} = {\rho /}2r$, ρ – радиус галтели переходной поверхности.

На рис. 3 дано графическое представление уравнения (7) – зависимости теоретического коэффициента концентрации напряжений от радиуса галтели ступенчатого вала.

Рис. 3.

Изменение теоретического коэффициента концентрации напряжений в зависимости от радиуса галтели ступенчатого вала.

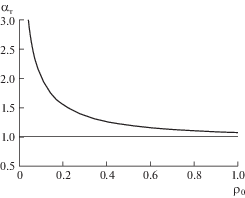
Полученная кривая хорошо согласуется с эмпирическими данными, приведенными в [11]. Отсюда можно заключить, что галтели ступенчатого вала с постоянным радиусом скругления не являются оптимальной формой переходной поверхности.

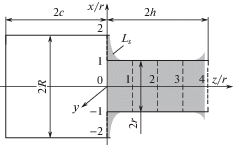
Для оптимизации формы переходной поверхности вала решим обратную задачу. Искривленное поле максимальных касательных напряжений (4) (рис. 2) разворачиваем на плоскости xz, тем самым получаем форму срединной поверхности вала в месте перехода ступень – основание, удовлетворяющую условию оптимальности [7, 11]

$\frac{{2{{\tau }_{{\max }}}}}{{{{\sigma }_{н}}}} = {{k}_{\sigma }} \to 1\quad {\text{или}}\quad s = \frac{{{{\tau }_{{\max }}}}}{{{{\sigma }_{н}}}} \to 0.5.~$

Математически развертка искривленной поверхности $s\left( {x{\text{/}}t;z{\text{/}}t} \right)$ выполняется путем определения длины ветви L_s функции s

${{L}_{s}}\left( {z{\text{/}}r} \right) = \pm \mathop \smallint \limits_0^{0.99r} \sqrt {1 + {{{\left( {\frac{{ds}}{{dx}}} \right)}}^{2}}} dx.$

Здесь знак “плюс” относится к интервалу 0 ≤ x ≤ +r, “минус” – к – r ≤ x ≤ 0 и, из-за того, что при x = r длина кривой L_s стремится к бесконечности, верхний предел интегрирования значением x = 0.99r.

В плоскости xz строим график L_s = f(z) в пределах $\left| {x{\text{/}}r} \right| \leqslant R{\text{/}}r$, $0 \leqslant z{\text{/}}r \leqslant 2h{\text{/}}r$, который представляет собой оптимальную форму переходной поверхности ступенчатого вала.

Результаты и их обсуждение. На рис. 4 изображена оптимальная форма переходной поверхности ступенчатого вала, рассчитанная по разработанной методике, при R = c = = h = 2r и β = 1.

Рис. 4.

Оптимальная форма переходной поверхности ступенчатого вала при R = c = h = 2r и β = 1.

Для проверки полученного результата проведены экспериментальные исследования напряженного состояния на плоских моделях из листового органического стекла толщиной δ = 6 мм при помощи лазерного полярископа по методике, описанной в [7]. Плоская модель срединной поверхности ступенчатого вала устанавливалась между опорными плитами нагрузочного устройства по схеме шарнирно опертой балки в крайних сечениях и сосредоточенной силой Р в месте переходной поверхности (z = 0). Чтобы исключить влияние контактных напряжений от жесткого индентора под действием силы Р, максимальные касательные напряжения определялись в точках модели при x ≤ 0.2r. Переходные поверхности моделей с постоянными радиусами скругления и оптимальной формы были изготовлены на фрезерно-гравировальном станке с ЧПУ (рис. 5).

Рис. 5.

Изготовление модели срединной поверхности ступенчатого вала.

Экспериментальное значение максимальных касательных напряжений определялось по формуле [7]

${{{\tau }}_{{{\text{max}}}}} = C\left( {{\text{arcsin}}\sqrt {\frac{U}{{{{U}_{{{\text{max}}}}}}}} - {\theta }} \right),$

где U – напряжение на фотоприемнике при нагружении модели силой P, мВ; C = = 2.226 МПа, θ = 0.181, U_max = 1500 мВ – тарировочные постоянные.

Основные результаты исследования для моделей при R = c = h = 2.1r = 25.2 мм, Р = = 60 Н, z = –2 мм и β = 0 представлены в табл. 1 и на рис. 6.

Таблица 1.

Результаты исследования максимальных касательных напряжений в модели срединной поверхности ступенчатого вала на лазерном полярископе

x, мм	Радиус галтели 5 мм		Радиус галтели 20 мм		Оптимальная форма
x, мм	U, мВ	τ_max, кПа	U, мВ	τ_max, кПа	U, мВ	τ_max, кПа
2.4	59	41.515	99	175.449	94	160.326
0	68	74.702	120	235.414	135	275.34
–2.4	110	207.52	193	413.761	257	547.064
–4.8	187	400.375	338	698.107	390	788.162
–7.2	370	754.038	500	967.152	560	1060.324
–9.6	560	1060.324	690	1256.255	718	1297.888
–12.0	1262	2181.705	824	1455.385	760	1360.231
–14.4	353	724.543	742	1339.454	573	1080.221
–16.8	196	420.387	461	905.122	281	593.494
–21.0	130	262.266	152	318.243	140	288.198

Рис. 6.

Напряженное состояние модели ступенчатого вала в переходном сечении при R = c = h = = 2.1r = 25.2 мм, x ≤ 0.2r, z = –2 мм и β = 0: I – с постоянным радиусом скругления ρ = 5 мм (ρ₀ = 0.21); II – с постоянным радиусом скругления ρ = 20 мм (ρ₀ = 0.83); III – с оптимальной формой переходной поверхности.

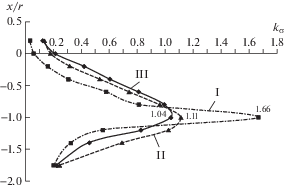
Обсуждение и заключения. 1. Из анализа эпюр (рис. 7) следует, что значения коэффициента концентрации напряжений α_T = k_σmax = 1.11 при ρ₀ = 0.83 и α_T = 1.66 при ρ₀ = 0.21 согласуются с теоретической кривой (рис. 3). 2. Наименьшее значение ${{{\alpha }}_{T}}$ составляет 1.04 для формы переходной поверхности L_s, рассчитанной по предложенной методике, что указывает на достижение поставленной цели исследований.

Список литературы

Francavilla A., Ramakrishnan C.V., Zienkiewicz O.C. Optimization of shape to minimize stress concentration // J. Strain Anal., 1975. V. 10. P. 63.
Sonmez F.O. Optimal shape design of shoulder fillets for flat and round bars under various loadings // J. Mechanical Engineering Science. 2009. V. 223. P. 1741.
Pedersen N.L. Optimization of Bolt Stress // 10th World Congress on Structural and Multidisciplinary Optimization, May 19–24, 2013, Orlando, Florida, USA. P. 1.
Yang L., Masatoshi S., Yoji S. Parameter-free method for the shape optimization of stiffeners on thin-walled structures to minimize stress concentration // Journal of Mechanical Science and Technology. 2015. V. 29. P. 1383.
Lian H., Christiansen A.N., Tortorelli D.A., Sigmund O., Aage N. Combined shape and topology optimization for minimization of maximal von Mises stress // Structural and multidisciplinary optimization. 2017. V. 55(5). P. 1541.
Мусхелишвили Н.И. Сингулярные интегральные уравнения. М.: Наука, 1968. 512 с.
Дородов П.В. Комплексный метод расчета и оптимального проектирования деталей машин с концентраторами напряжений: Монография. Ижевск: ФГБОУ ВПО Ижевская ГСХА, 2014. 316 с.
Кулиев В.Д. Новые эффективные методы решения класса смешанных краевых задач // Вестник ЧГПУ им. И.Я. Яковлева. 2015. № 1(23). С. 132.
Урбанович Т.М. Об особом случае характеристического уравнения с ядром Коши // Дифференциальные уравнения. 2015. Т. 52. № 12. С. 1650.
Урбанович Т.М. Особый случай сингулярного интегрального уравнения с ядром Коши // Доклады НАН Беларуси. 2016. Т. 60. № 2. С. 10.
Ерохин М.Н., Дородов П.В. Метод оптимизации формы несимметричных ступенчатых деталей // Международный технико-экономический журнал. 2016. № 2. С. 10.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал