Проблемы машиностроения и надежности машин, 2020, № 3, стр. 79-93
АНАЛИЗ ЭФФЕКТИВНОСТИ КОЛЬЦЕВЫХ И ЛЕНТОЧНЫХ ПРУЖИН ИЗ СТЕКЛОПЛАСТИКА
А. Н. Полилов 1, *, Н. А. Татусь 1, В. В. Жавыркин 1, Ш. Тян 2
1 Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия
2 Xi'an Jiaotong University, провинция Шэньси
Сиань, Китай
* E-mail: polilovan@mail.ru
Поступила в редакцию 19.12.2018
Принята к публикации 31.01.2020
Аннотация
Изложен метод проектного расчета кассетно-кольцевых и волнистых ленточных пружин из однонаправленного, высокопрочного и низкомодульного стеклопластика, предназначенных в качестве упругой подвески для транспортных средств и летательных аппаратов. Использование разрезных колец с различными зазорами позволяет получить нелинейное изменение податливости подвески. Проанализированы эффекты от создания равнопрочного профилирования ленточных волнистых пружин. Замена стальных пружин на композитные позволяет обеспечить многократное снижение массы при сохранении требований по прочности и податливости.
Стеклопластик на основе непрерывных высокопрочных стеклянных волокон обладает уникальными свойствами для упругих элементов, так как возможная накопленная в нем энергия в расчете на единицу массы оказывается наибольшей по сравнению со всеми известными конструкционными материалами (табл. 1).
Таблица 1.
Способность различных материалов запасать упругую энергию $U{\text{*}}$ на единицу объема $V$ или массы $\rho V$ (приведены предельные деформации $\varepsilon {\text{*}}$ и напряжения при растяжении $\sigma {\text{*}}$)
| Материал | $\varepsilon {\text{*}}$, % | $\sigma {\text{*}}$, МПа | $U{\text{*/}}V$, МДж/м3 | $\rho $, 103 кг/м3 | $U{\text{*/}}(\rho V)$, КДж/кг |
|---|---|---|---|---|---|
| Пружинная сталь | 0.3 | 700 | 1.0 | 7.8 | 0.13 |
| Бронза | 0.3 | 400 | 0.6 | 8.7 | 0.06 |
| Древесина тиса | 0.9 | 120 | 0.5 | 0.6 | 0.83 |
| Материал рога | 4.0 | 90 | 1.8 | 1.2 | 1.5 |
| Сухожилие | 8.0 | 70 | 2.8 | 1.1 | 2.5 |
| Резина | 300 | 7.0 | 10.0 | 1.2 | 8.0 |
| Стеклопластик (0) | 2.0 | 1000 | 10.0 | 1.9 | 5.3 |
Это связано с высокой прочностью и малым модулем упругости стеклопластика при низкой плотности и практически линейной диаграмме деформирования. В то же время, полимерная матрица обладает способностью к демпфированию и шумопоглощению. Именно эти качества определяют эффективность стеклопластика при создании упругих элементов – накопителей энергии: лука, шеста для прыжков, торсиона, кольцевой подвески (раздел 1), ленточных пружин (раздел 2), рессор [1–3]. Еще больший эффект достигается возможностью создавать из стеклопластика профилированные или ветвящиеся упругие элементы [1–3], что для ленточных и кольцевых пружин проиллюстрировано в разделе 3. Кроме инженерных аналитических расчетов [4–7] анализ эффективности профилированных ленточных пружин подтвержден компьютерным моделированием (раздел 4) и пробными экспериментами на полимерных образцах (раздел 5), изготовленных на 3-D принтере.
Авторы видят применение результатов работы для расчета упругих элементов аэрокосмических изделий, где наиболее важным показателем эффективности является снижение массы, поэтому в статье не рассматриваются характерные для подвески автомобилей циклическое нагружение, пробои и удары.
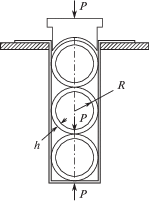
1. Кольцевая кассетная подвеска из целых и разрезных колец. На рис. 1 представлена схема кассетной (“магазинной” – magazine) пружины, состоящей из сжимаемых вдоль диаметра колец, которые вырезаны из композитной трубы с окружной намоткой. Добавление нескольких наружных слоев под углами ±45° позволяет существенно повысить поперечную прочность и сопротивление кручению без заметного снижения модуля упругости и предела прочности в окружном направлении.
1.1. Методы расчета прочности, податливости и накопленной упругой энергии
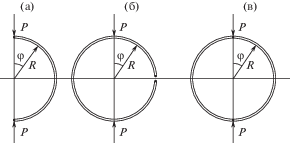
Разрезное кольцо. Для оценки податливости С подвески рассмотрим диаметрально нагруженное силами Р тонкостенное кольцо со средним радиусом R, толщиной h и шириной w. Если разрезное кольцо имеет зазор, то смещение точек приложения сил можно оценить по схеме нагружения полукольца (рис. 2а, б).
Рис. 2.
Схема нагружения для расчета податливости полукольца – (а), разрезного – (б) и сплошного кольца – (в).
Простейший подход к оценке перемещений основан на энергетическом принципе Кастильяно, приводящем к интегралу Мора.
Для одного полукольца работа силы Р на искомом перемещении u1 приравнивается накопленной в полукольце упругой энергии $U$, выраженной через изгибающий момент
(2)
${{U}_{1}} = \frac{1}{2}P{{u}_{1}} = \frac{1}{2}\int\limits_0^\pi {\frac{{{{M}^{2}}\left( \varphi \right)}}{{EI}}} Rd\varphi ,$Данный подход основан на ряде допущений: не учитываются деформации от продольных сил и дополнительные прогибы от межслойных сдвигов. Радиус считается значительно превосходящим толщину, и поэтому локальное изменение кривизны кольца под действием изгибающего момента рассчитывается по формуле для прямой балки. В результате из (1), (2) оценивается податливость одного полукольца
(3)
${{C}_{1}} = \frac{{{{u}_{1}}}}{P} = \frac{{{{R}^{3}}}}{{EI}}\int\limits_0^\pi {{{{\sin }}^{2}}\varphi } d\varphi = \frac{{\pi {{R}^{3}}}}{{2EI}} \approx 1.57\frac{{{{R}^{3}}}}{{EI}},$Наибольшее напряжение ${{\sigma }_{{\max }}}$ в полукольце или в разрезном кольце можно выразить через максимальную приложенную нагрузку ${{P}_{{\max }}}$
(4)
${{\sigma }_{{\max }}} = \frac{{6{{P}_{{\max }}}R}}{{w{{h}^{2}}}} = {{\beta }_{1}}\frac{{{{P}_{{\max }}}R}}{{w{{h}^{2}}}}.$Сплошное кольцо. Схема деформирования сплошного кольца диаметральными силами (рис. 2в) требует более сложного рассмотрения с использованием дифференциального уравнения равновесия, но результат по размерности получается сходным с (3). Отсылая читателя за подробным выводом к литературе по строительной механике, выпишем только основные соотношения и результаты.
Связь изменения кривизны $\kappa $ с изгибающим моментом $M$ считается такой же, как для прямого бруса: $\kappa = \frac{M}{{EI}}$, но изменение кривизны можно выразить также через радиальное смещение ${{u}_{r}}$ кольца: $\kappa = - \frac{1}{{{{R}^{2}}}}\left( {\frac{{{{d}^{2}}{{u}_{r}}}}{{d{{\varphi }^{2}}}} + {{u}_{r}}} \right)$, откуда получается дифференциальное уравнение для нерастяжимой упругой линии
(5)
$\frac{{{{d}^{2}}{{u}_{r}}}}{{d{{\varphi }^{2}}}} + {{u}_{r}} = - \frac{{M{{R}^{2}}}}{{EI}} = \frac{{P{{R}^{3}}}}{{EI}}\left( {\frac{1}{2}\sin \varphi - \frac{1}{\pi }} \right).$В (5) использовано полученное из уравнений равновесия распределение изгибающих моментов, и решая (5) в тригонометрических функциях, найдем константы интегрирования с учетом симметрии и граничных условий. Окончательная зависимость радиальных смещений от полярного угла имеет вид
(6)
${{u}_{r}} = \frac{{P{{R}^{3}}}}{{EI}}\left( {\frac{1}{4}\sin \varphi + \frac{\pi }{8}\cos \varphi - \frac{1}{4}\varphi \cos \varphi - \frac{1}{\pi }} \right).$Податливость сплошного кольца ${{C}_{2}}$ можно выразить из (6) через относительное смещение ${{u}_{2}} = 2{{u}_{r}}$ точек приложения сил для φ = 0 и φ = π
(7)
${{C}_{2}} = \frac{{{{u}_{2}}}}{P} = \frac{{{{R}^{3}}}}{{EI}}\left( {\frac{\pi }{4} - \frac{2}{\pi }} \right) \approx 0.149\frac{{{{R}^{3}}}}{{EI}},$Для n колец фиксированного радиуса R податливость всей подвески в n раз больше, чем для одного кольца.
Для сплошного кольца наибольший момент ${{M}_{{{\text{max}}}}} = {{P}_{{{\text{max}}}}}R{\text{/}}\pi $ действует в точках приложения сил, и наибольшее напряжение оказывается примерно в 3 раза ниже, чем в (4) для полукольца
(9)
${{\sigma }_{{\max }}} = \frac{{6{{P}_{{\max }}}R}}{{\pi w{{h}^{2}}}} = {{\beta }_{2}}\frac{{{{P}_{{\max }}}R}}{{w{{h}^{2}}}}.$Другой способ оценки податливости сплошного кольца описан С.П. Тимошенко со ссылкой на ранние работы лорда Релея (J.W. Strutt). Радиальное перемещение представим в виде ряда
(10)
${{u}_{r}} = \sum\limits_j {\left[ {{{a}_{j}}\cos \left( {j\varphi } \right) + {{b}_{j}}\sin \left( {j\varphi } \right)} \right]} .$Деформация оси кольца выражается через радиальное ${{u}_{r}}$ и окружное ${{u}_{\varphi }}$ перемещения: $\varepsilon = \frac{1}{R}\left( {\frac{{d{{u}_{\varphi }}}}{{d\varphi }} - {{u}_{r}}} \right)$, и из гипотезы о нерастяжимости нейтральной линии кольца $\varepsilon = 0$ получим
(11)
$\frac{{d{{u}_{\varphi }}}}{{d\varphi }} - {{u}_{r}} = 0 \Rightarrow {{u}_{\varphi }} = \sum\limits_{j = 2}^\infty {\frac{1}{j}\left[ {{{a}_{j}}\cos \left( {j\varphi } \right) - {{b}_{j}}\sin \left( {j\varphi } \right)} \right]} .$Значение $j = 1$ исключено, так как оно соответствует перемещению кольца как жесткого целого.
Чтобы найти в (11) неизвестные коэффициенты, применим принцип возможных перемещений и сравним накопленную упругую энергию с работой сил. Упругую энергию выразим через изменение кривизны
(12)
${{U}_{2}} = \frac{{EI}}{2}\int\limits_0^{2\pi } {\left( {\frac{1}{r} - \frac{1}{R}} \right)Rd\varphi } = \frac{{EI}}{{2{{R}^{3}}}}\int\limits_0^{2\pi } {{{{\left( {\frac{{{{d}^{2}}{{u}_{r}}}}{{d{{\varphi }^{2}}}} + {{u}_{r}}} \right)}}^{2}}d\varphi } = \frac{{EI\pi }}{{2{{R}^{3}}}}\sum\limits_{j = 2}^\infty {[{{{({{j}^{2}} - 1)}}^{2}}(a_{j}^{2} + b_{j}^{2})].} $Сравнивая упругую энергию (12) с работой диаметральных сил на перемещении ${{u}_{r}}$ при φ = 0 и φ = π, найдем, что отличными от нуля останутся только коэффициенты ${{a}_{j}}$ при четных значениях $j$. Окончательно сближение точек приложения сжимающих сил выразится как удвоенное перемещение ${{u}_{r}}(0)$ в виде быстро сходящегося ряда
(13)
${{u}_{2}} = \frac{{4P{{R}^{3}}}}{{\pi EI}}\sum\limits_{j = 2,4, \ldots }^\infty {{{{({{j}^{2}} - 1)}}^{{ - 2}}}} = \frac{{4P{{R}^{3}}}}{{\pi EI}}\left( {\frac{1}{9} + \frac{1}{{225}} + \frac{1}{{1225}} \ldots } \right) \approx 0.148\frac{{P{{R}^{3}}}}{{EI}}.$Результат (13) определения податливости кольца при диаметральном сжатии практически совпадает с (7) и его можно использовать при инженерных расчетах упругой подвески кассетного типа (рис. 1).
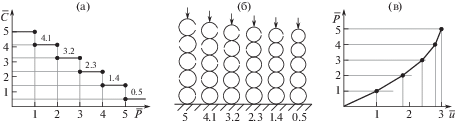
1.2. Нелинейное изменение податливости при выборе зазоров. Если стеклопластиковые кольца сплошные, то податливость подвески оказывается довольно низкой (хотя и выше примерно в пять раз, чем у аналогичной стальной пружины). Но если использовать разрезные кольца с разными зазорами, то можно получить податливую и нелинейную подвеску. Податливость при диаметральном сжатии сплошного кольца, как видно из (3), (7), (13), примерно, в 10 раз ниже, чем у разрезного кольца, а податливость, например, пяти колец – в пять раз выше. Условно примем податливость разрезного кольца за единицу. Считаем, что зазоры в кольцах неодинаковые, например: 1, 2, 3, 4, 5 (для наглядности – миллиметров). Пока все пять колец свободно деформируются и их зазоры не выбраны, суммарная податливость составляет пять единиц. По мере роста нагрузки сжатия (в силу линейности задачи – кратно зазорам, например, до 10, 20, 30, 40, 50 кг) один за другим будут выбираться зазоры, и податливость будет последовательно уменьшаться (рис. 3, показано стрелками). Сначала одно кольцо станет в десять раз более жестким, потом – второе, и так – пока податливость всей подвески не станет в десять раз меньше: 5 → 4.1 → 3.2 → 2.3 → 1.4 → 0.5. В результате получается сильно нелинейная (иногда это необходимо) подвеска.
Рис. 3.
Нелинейное изменение податливости (а) кассетной кольцевой подвески (б) по мере выбора различных зазоров разрезных колец при сжатии. Зависимость нагрузки от выбранных зазоров (в). $\bar {P}$, $\bar {C}$, $\bar {u}$ – приведенные сила, податливость и ход подвески.
1.3. Расчет на прочность при заданной податливости. Техническое задание при проектном расчете пружин из $n$ колец включает два основных, противоречивых требования: 1) по прочности – максимальное напряжение (4) или (9) не превышает предела прочности ${{\sigma }_{{\text{*}}}}$
(14)
${{\sigma }_{{\max }}} = {{\beta }_{i}}\frac{{{{P}_{{\max }}}R}}{{w{{h}^{2}}}} \leqslant {{\sigma }_{ * }};\quad \left( {{{\beta }_{1}} = 6;\quad {{\beta }_{2}} \approx 1.91} \right);$2) по заданной податливости (8)
или заданной накопленной упругой энергии ${{U}_{ * }}$Из точного выполнения условия (14) по прочности при заданной податливости (15) или заданной накопленной энергии (16) можно найти необходимые толщину, число n и суммарную массу m колец подвески из стеклопластика с плотностью $\rho $
(17)
$\begin{gathered} h = \sqrt {\frac{{{{\beta }_{i}}{{P}_{{max}}}R}}{{w{{\sigma }_{ * }}}}} ;\quad n = \frac{{{{C}_{ * }}E}}{{{{\alpha }_{i}}}}\sqrt {\frac{{\beta _{i}^{3}P_{{\max }}^{3}}}{{w\sigma _{ * }^{3}{{R}^{3}}}}} = \frac{{2{{U}_{ * }}E}}{{{{\alpha }_{i}}}}\sqrt {\frac{{\beta _{i}^{3}}}{{wP_{{\max }}^{{}}\sigma _{ * }^{3}{{R}^{3}}}}} ; \\ m \approx 2\pi \rho nRhw = \frac{{2\pi \rho \beta _{i}^{2}{{C}_{ * }}EP_{{max}}^{2}}}{{{{\alpha }_{i}}\sigma _{ * }^{2}}} = \frac{{4\pi \rho \beta _{i}^{2}{{U}_{ * }}E}}{{{{\alpha }_{i}}\sigma _{ * }^{2}}}. \\ \end{gathered} $Для разрезных колец прочность меньше, чем у сплошных колец, но податливость выше, и числовые коэффициенты в формуле (17) для массы несколько различаются: $\frac{{\beta _{1}^{2}}}{{{{\alpha }_{1}}}} = \frac{6}{\pi } = 1.91$; $\frac{{\beta _{2}^{2}}}{{{{\alpha }_{2}}}} = 2.03$, т.е. кассетная подвеска из разрезных колец может быть на 6% легче, чем из сплошных.
Как следует из (17), минимально возможная масса кассетно-кольцевой подвески практически не зависит от размера колец, а зависит лишь от модуля упругости Е, прочности ${{\sigma }_{ * }}$ и плотности ρ при заданных податливости (упругой энергии) и предельной нагрузке. Учитывая, что модуль упругости стеклопластика ${{E}^{g}} = 45$ ГПа примерно в пять раз ниже, чем у стали, а плотность в три раза ниже при примерно равной прочности, получаем возможность снижения массы в пятнадцать раз и уменьшения числа колец, т.е. длины подвески в пять раз. Даже, если принять усталостную прочность стеклопластика в два раза ниже, чем у стали, сохраняется возможность снижения массы подвески примерно в четыре раза (без учета массы самой кассеты и узлов крепления).
2. Пружины из волнистых лент. Отмеченные преимущества стеклопластика относятся и к подвеске, схематически изображенной на рис. 4, из композитных волнистых лент (N = 4), испытывающих растяжение-сжатие, так как смещение происходит за счет их изгиба. Такие ленты можно изготавливать выкладкой препрегов в волнистую пресс-форму или методом пулформинга [9]. Требования по прочности (14) и податливости (15) остаются прежними. Для качественных оценок (с точностью до числового коэффициента) можно использовать решение для сжатия N лент, каждая из которых состоит из n полуколец.
Пояснения корректности постановки задачи и применяемых методов. 1. Расчет прогибов в криволинейных лентах проводился с применением интеграла Мора. При изгибе кривого бруса сечения не остаются плоскими, происходит смещение нейтральной оси. Но все это важно для толстых брусьев типа крюка крана. Поправка к обычному решению пропорциональна отношению толщины кольца к радиусу, поэтому для тонких лент ее можно не учитывать.
2. Разумеется, при изгибе полукольца изменяется плечо действия силы и, следовательно, изгибающий момент. При этом полуокружность переходит в полуэллипс при сохранении длины нейтральной линии. Одна полуось в результате прогиба уменьшается, а другая увеличивается, вызывая увеличение изгибающего момента при постоянной диаметральной силе. Можно попытаться найти выражение для длины контура полуэллипса. Со времен Л. Эйлера этим занимались десятки ученых, но эта длина (в отличие от длины окружности) не выражается через элементарные функции, а приводит к (табулированным), “неберущимся” эллиптическим интегралам. Никакой заменой переменных их нельзя свести к табличным. Поэтому в инженерных приложениях учет изменения момента в кривых стержнях крайне затруднителен, что видно из приведенного в конце статьи Приложения. Это пояснено данными ниже формулами.
3. Стеклопластик проявляет наследственно упругие свойства. Можно ли ограничиться линейно упругим приближением? Однонаправленный стеклопластик обладает практически линейной диаграммой деформирования до предельной деформации порядка 2–3% (не 0.2% как у стали). Поэтому при нагружении в упругой области (вплоть до больших перемещений ленточных пружин) реологические эффекты можно не учитывать. Был пример из опыта работы в ИМАШ со стеклопластиковыми рессорами. После испытаний рессора была зафиксирована (заневолена) в нагруженном состоянии при своем максимальном прогибе порядка 300 мм. В таком состоянии рессора хранилась более 15 лет. Затем работы по рессорам были продолжены, и эта старая рессора была вновь испытана. Стрела прогиба практически восстановилась, а измеренное при изгибе значение модуля упругости после многолетнего нахождения под максимальной нагрузкой оказалось лишь на 2% меньше значения, измеренного 15 лет назад. Вязкоупругие свойства практически не проявились.
Поэтому далее рассмотрено линейное, “балочное” приближение.
Смещение концов полукольца (рис. 2а) под действием силы Р/N выражается из (3), (8) в виде ${{u}_{1}} = \frac{u}{n}$ = $\frac{{\pi P{{R}^{3}}}}{{2NEI}}$, и податливость ленточной пружины из N лент, каждая из которых состоит из n полуколец
Максимальное напряжение в полукольце должно не превышать допустимого значения
(19)
${{\sigma }_{{\max }}} = \frac{{6{{P}_{{\max }}}R}}{{Nw{{h}^{2}}}} \leqslant {{\sigma }_{ * }}.$Из одновременного выполнения условия заданной податливости (18) и равенства в условии прочности (19) находим по аналогии с (17) необходимое число полуколец (полуволн), толщину лент и их минимально возможную суммарную массу
(20)
$n = \sqrt {\frac{{6С_{ * }^{2}{{E}^{2}}P_{{\max }}^{3}}}{{{{\pi }^{2}}Nw{{R}^{3}}\sigma _{ * }^{3}}}} ;\quad h = \sqrt {\frac{{6{{P}_{{\max }}}R}}{{{{\sigma }_{ * }}wN}}} ;\quad {{m}_{0}} \approx \pi \rho NnRwh = \frac{{6\rho P_{{\max }}^{2}E{{C}_{ * }}}}{{\sigma _{ * }^{2}}} = \frac{{12\rho E{{U}_{ * }}}}{{\sigma _{ * }^{2}}}.$Как видно из (20), минимально возможная масса листовой пружины из волнистых лент (из полуколец) вдвое меньше оценки (17) для разрезных колец (просто, масса кольца вдвое больше, чем полукольца), и она при заданных жесткости и предельной нагрузке не зависит от радиуса R, числа волн n и лент N, а зависит лишь от модуля упругости Е, прочности ${{\sigma }_{ * }}$ и плотности ρ.
За счет низких плотности и модуля, высокой прочности и линейной упругости ленточные волнистые пружины из стеклопластика оказываются по массе и по долговечности значительно эффективнее стальных упругих элементов.
3. Энергетический метод анализа возможного снижения массы за счет профилирования
3.1. Диаметрально нагруженное равнопрочное полукольцо. Поскольку изгибающий момент (1) в диаметрально сжимаемом полукольце пропорционален синусу полярного угла, можно применить равнопрочное профилирование (кроме концевых участков с постоянными размерами сечения)
(21)
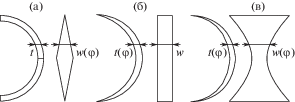
$\begin{gathered} {{w}_{i}}\left( \varphi \right)h_{i}^{2}\left( \varphi \right) = {{w}_{{ * i}}}h_{{ * i}}^{2}\sin \varphi ;\quad {{\varphi }_{{_{0}}}} \leqslant \varphi \leqslant {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}; \\ {{w}_{i}}\left( \varphi \right) = {{w}_{i}}\left( {{{\varphi }_{0}}} \right);\quad {{h}_{i}}\left( \varphi \right) = {{h}_{i}}\left( {{{\varphi }_{0}}} \right);\quad 0 \leqslant \varphi \leqslant {{\varphi }_{{_{0}}}}; \\ {{w}_{{ * i}}} = {{w}_{i}}\left( {{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right);\quad h_{{ * i}}^{{}} = {{h}_{i}}\left( {{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right). \\ \end{gathered} $В (21) и далее нижний индекс $i$ означает один из наиболее естественных типов равнопрочного полукольца с постоянными: толщиной $i = 1$ (рис. 5а), шириной $i = 2$ (рис. 5б) или площадью сечения (констэра) $i = 3$ (рис. 5в); $i = 0$ относится к полукольцу с постоянными размерами сечений.
Объем таких профилированных полуколец и накопленную в них упругую энергию можно рассчитать интегрированием
(22)
$\begin{gathered} {{V}_{{ * i}}} = 2R\left[ {\int\limits_{{{\varphi }_{0}}}^{\pi /2} {{{w}_{i}}\left( \varphi \right){{h}_{i}}\left( \varphi \right)d\varphi } + {{w}_{i}}\left( {{{\varphi }_{0}}} \right){{h}_{i}}\left( {{{\varphi }_{0}}} \right)\int\limits_0^{{{\varphi }_{0}}} {d\varphi } } \right] = {{V}_{{0i}}}{{\delta }_{{Vi}}};\quad {{V}_{{0i}}} = \pi R{{w}_{{ * i}}}{{h}_{{ * i}}}; \\ {{U}_{{ * i}}} = \frac{{{{P}^{2}}{{R}^{3}}}}{E}\left[ {\int\limits_{{{\varphi }_{0}}}^{\pi /2} {\frac{{{{{\sin }}^{2}}\varphi }}{{{{I}_{i}}\left( \varphi \right)}}d\varphi } + \int\limits_0^{{{\varphi }_{0}}} {\frac{{{{{\sin }}^{2}}\varphi }}{{{{I}_{i}}\left( {{{\varphi }_{0}}} \right)}}d\varphi } } \right] = {{U}_{{0i}}}{{\delta }_{{Ui}}};\quad {{U}_{{0i}}} = \frac{{\pi {{P}^{2}}{{R}^{3}}}}{{4E}}\frac{{12}}{{{{w}_{{ * i}}}h_{{ * i}}^{3}}}. \\ \end{gathered} $Для случая профилированного полукольца из условий прочности (19) при наибольшей нагрузке ${{P}_{ * }}$ и заданной накопленной энергии ${{U}_{ * }}$ (16) можно из (22) найти требуемые размеры наиболее нагруженного центрального сечения
(23)
${{\sigma }_{ * }} = \frac{{6{{P}_{{\text{*}}}}R}}{{{{w}_{{ * i}}}h_{{ * i}}^{2}}};\quad {{U}_{{\text{*}}}} = {{U}_{{0i}}}{{\delta }_{{Ui}}} \Rightarrow {{h}_{{{\text{*}}i}}} = \frac{{\pi {{\sigma }_{{\text{*}}}}{{P}_{{\text{*}}}}{{R}^{2}}{{\delta }_{{Ui}}}}}{{2E{{U}_{{\text{*}}}}}};\quad {{w}_{{ * i}}} = \frac{{24{{E}^{2}}U_{{\text{*}}}^{2}}}{{{{\pi }^{2}}\sigma _{{\text{*}}}^{3}{{P}_{{\text{*}}}}{{R}^{3}}\delta _{{Ui}}^{2}}}.$Из (23) по аналогии с (17) можно оценить необходимую массу профилированного полукольца и сравнить его с массой (20) однородного полукольца, удовлетворяющего тем же условиям по прочности и накопленной энергии
(24)
$m \approx \pi \rho R{{w}_{{ * i}}}{{h}_{{ * i}}}{{\delta }_{{Vi}}} = \frac{{12\rho E{{U}_{{\text{*}}}}}}{{\sigma _{{\text{*}}}^{2}}}\frac{{{{\delta }_{{Vi}}}}}{{{{\delta }_{{Ui}}}}} = {{m}_{0}}{{\delta }_{m}}.$В (24) у коэффициента формы по массе ${{\delta }_{m}} = {{\delta }_{{Vi}}}{\text{/}}{{\delta }_{{Ui}}}$ индекс i специально опущен, чтобы подчеркнуть, что для всех “идеальных” равнопрочных полуколец (см. ниже) этот коэффициент одинаков и равен 1/2.
1) полукольцо с постоянной толщиной ${{h}_{1}}(\pi {\text{/}}2) = {{h}_{{{\text{*}}1}}}$ (рис. 5а). Из (21)
(25)
$\begin{gathered} {{h}_{1}}\left( \varphi \right) = {{h}_{{\text{*}}}}_{1};\quad {{w}_{1}}\left( \varphi \right) = {{w}_{{\text{*}}}}_{1}\sin \varphi \quad при\quad {{\varphi }_{0}} \leqslant \varphi \leqslant \pi {\text{/}}2; \\ {{h}_{1}}\left( \varphi \right) = {{h}_{{\text{*}}}}_{1};\quad {{w}_{1}}\left( \varphi \right) = {{w}_{{\text{*}}}}_{1}sin{{\varphi }_{0}}\quad при\quad 0 \leqslant \varphi \leqslant {{\varphi }_{0}}. \\ \end{gathered} $Согласно (22) коэффициенты формы по объему ${{\delta }_{{V1}}}$, накопленной энергии ${{\delta }_{{U1}}}$ и массе ${{\delta }_{{m1}}}$ для полукольца типа 1 определяются выражениями
2) полукольцо с постоянной шириной ${{w}_{1}}\left( {{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right) = {{w}_{{\text{*}}}}_{1}$ (рис. 5б). Из условия равнопрочности (21)
Этот случай оказывается сложнее для аналитики, так как интегралы не берутся в квадратурах, однако, окончательный вывод о снижении массы за счет равнопрочного профилирования остается прежним
(26)
$\begin{gathered} {{\delta }_{{V2}}} = \frac{{{{V}_{2}}}}{{{{V}_{0}}}} = \frac{2}{\pi }\left[ {X + {{\varphi }_{0}}\sin {{\varphi }_{0}}} \right]\;\xrightarrow[{{{\varphi }_{0}} \to 0}]{}\;\frac{2}{\pi }X;\;\;(\xrightarrow[{{{\varphi }_{0}} \to \pi /2}]{}\;1);\quad X = \int\limits_{{{\varphi }_{0}}}^{\pi /2} {\sqrt {\sin \varphi } d\varphi ;} \\ {{\delta }_{{U2}}} = \frac{{{{U}_{2}}}}{{{{U}_{0}}}} = \frac{4}{\pi }\left[ {X + \int\limits_0^{{{\varphi }_{0}}} {\frac{{{{{\sin }}^{2}}\varphi }}{{{{{\sin }}^{{3/2}}}{{\varphi }_{0}}}}d\varphi } } \right] = \frac{4}{\pi }\left[ {X + \frac{{{{\varphi }_{0}} - \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} \sin 2{{\varphi }_{0}}}}{{2{{{\sin }}^{{3/2}}}{{\varphi }_{0}}}}} \right]\;\xrightarrow[{{{\varphi }_{0}} \to 0}]{}\;\frac{{4X}}{\pi }; \\ \Rightarrow {{\delta }_{{m1}}}\;\xrightarrow[{{{\varphi }_{0}} \to 0}]{}\;\frac{1}{2}. \\ \end{gathered} $3) Полукольцо с постоянной площадью сечения – констэра
(27)
$\begin{gathered} {{h}_{3}}\left( \varphi \right) = {{h}_{{\text{*}}}}_{3}\sin \varphi ;\quad {{w}_{3}}\left( \varphi \right) = {{w}_{{\text{*}}}}_{3}{{\sin }^{{ - 1}}}\varphi \quad при\quad {{\varphi }_{0}} \leqslant \varphi \leqslant \pi {\text{/}}2; \\ {{h}_{3}}\left( \varphi \right) = {{h}_{{\text{*}}}}_{3}\sin {{\varphi }_{0}};\quad {{w}_{1}}\left( \varphi \right) = {{w}_{{\text{*}}}}_{1}{{\sin }^{{ - 1}}}{{\varphi }_{0}}\quad при\quad 0 \leqslant \varphi \leqslant {{\varphi }_{0}}. \\ \end{gathered} $Этот вариант равнопрочного профилирования наиболее предпочтителен для волокнистых композитов, так как сохранение площади сечения позволяет использовать постоянное число непрерывных волокон, что принципиально для сохранения прочности при профилировании. Хотя площадь сечения сохраняется, за счет роста податливости, а значит – накопленной упругой энергии – коэффициент снижения массы оказывается прежним
(28)
$\begin{gathered} {{\delta }_{{V3}}} = \frac{{{{V}_{3}}}}{{{{V}_{0}}}} = \frac{2}{\pi }\left[ {\int\limits_{{{\varphi }_{0}}}^{\pi /2} {d\varphi } + \int\limits_0^{{{\varphi }_{0}}} {d\varphi } } \right] = 1; \\ {{\delta }_{{U3}}} = \frac{{{{U}_{3}}}}{{{{U}_{0}}}} = \frac{4}{\pi }\left[ {\int\limits_{{{\varphi }_{0}}}^{\pi /2} {d\varphi } + \int\limits_0^{{{\varphi }_{0}}} {\frac{{{{{\sin }}^{2}}\varphi }}{{{{{\sin }}^{2}}{{\varphi }_{0}}}}d\varphi } } \right] = \\ = \frac{4}{\pi }\left[ {\frac{\pi }{2} - {{\varphi }_{0}} + \frac{{{{\varphi }_{0}} - {\text{1/2}}\sin 2{{\varphi }_{0}}}}{{2{{{\sin }}^{2}}{{\varphi }_{0}}}}} \right]\;\xrightarrow[{{{\varphi }_{0}} \to 0}]{}\;2;\;\;\left( {\xrightarrow[{{{\varphi }_{0}} \to \pi /2}]{}1} \right); \\ {{\delta }_{{m3}}} = \frac{{{{\delta }_{{V3}}}}}{{{{\delta }_{{U3}}}}}\;\xrightarrow[{{{\varphi }_{0}} \to 0}]{}\;\frac{1}{2}. \\ \end{gathered} $Приведенные результаты иллюстрируют, что любое диаметрально нагруженное, “идеально” равнопрочное полукольцо при заданных прочности и накопленной энергии вдвое легче, чем полукольцо с постоянными размерами сечений.
Реально не удастся достичь такого снижения массы благодаря только профилированию из-за невозможности создать неограниченно широкое и бесконечно тонкое полукольцо типа констэра, но за счет высокой прочности, низкой плотности и низкого модуля Юнга стеклопластик в подобных пружинах из волнистых лент способен обеспечить снижение массы примерно в пятнадцать раз по сравнению со стальным аналогом.
3.2. Эффективность равнопрочных балок при разных условиях нагружения. Приведенные выше иллюстрации можно обобщить на случай консольной балки длины $l$ под действием изгибающего момента, изменяющегося по произвольному степенному закону
(29)
$M\left( {\bar {x}} \right) = M\left( 1 \right){{\bar {x}}^{\gamma }};\quad \bar {x} = {x \mathord{\left/ {\vphantom {x l}} \right. \kern-0em} l}.$Примем изменения размеров прямоугольных сечений для выполнения условия равнопрочности согласно (29) в степенном виде
(30)
$w\left( {\bar {x}} \right) = w\left( 1 \right){{\bar {x}}^{\alpha }};\quad h\left( {\bar {x}} \right) = h\left( 1 \right){{\bar {x}}^{\beta }};\quad \sigma = \frac{{6M}}{{w{{h}^{2}}}} \Rightarrow \alpha + 2\beta = \gamma .$Случай концевой силы соответствует $\gamma = 1$, равномерно распределенная нагрузка – $\gamma = 2$, линейно растущая от конца балки нагрузка – $\gamma = 3$.
С помощью теоремы Кастильяно можно сразу, без вычисления прогибов, оценить накопленную упругую энергию в балке с переменным сечением под действием изменяющегося по длине момента
(31)
${{U}_{{\text{*}}}} = \frac{{6l}}{E}\int\limits_0^l {\frac{{{{M}^{2}}\left( {\bar {x}} \right)}}{{w\left( {\bar {x}} \right){{h}^{3}}\left( {\bar {x}} \right)}}d\bar {x}.} $Из заданных значений максимального момента $M(1)$, прочности ${{\sigma }_{{\text{*}}}}$ (32, п. 1) и упругой энергии ${{U}_{{\text{*}}}}$ (32, п. 2) найдем требуемые размеры корневого сечения профилированной равнопрочной балки
(32)
$\begin{gathered} 1.\quad {{\sigma }_{*}} = \frac{{6M\left( 1 \right)}}{{w\left( 1 \right){{h}^{2}}\left( 1 \right)}}; \\ 2.\quad {{U}_{*}} = \frac{{6{{M}^{2}}\left( 1 \right)l}}{{Ew\left( 1 \right){{h}^{3}}\left( 1 \right)}}\int\limits_0^1 {{{{\bar {x}}}^{{2\gamma - \alpha - 3\beta }}}d\bar {x}} = {{U}_{0}}{{\delta }_{U}};\quad {{\delta }_{U}} = \frac{{1 + 2\gamma }}{{1 + 2\gamma - \alpha - 3\beta }}; \\ {\text{из}}\quad 1.{\kern 1pt} - {\kern 1pt} 2. \Rightarrow h\left( 1 \right) = \frac{{{{\sigma }_{*}}M\left( 1 \right)l}}{{{{U}_{*}}E\left( {1 + 2\gamma - \alpha - 3\beta } \right)}} = {{h}_{0}}{{\delta }_{U}}; \\ w\left( 1 \right) = \frac{{6U_{*}^{2}{{E}^{2}}{{{\left( {1 + 2\gamma - \alpha - 3\beta } \right)}}^{2}}}}{{\sigma _{*}^{3}M\left( 1 \right){{l}^{2}}}} = {{w}_{0}}\delta _{U}^{{ - 2}};\quad {{\delta }_{V}} = \frac{{{{V}_{s}}}}{{{{V}_{0}}}} = \int\limits_0^1 {{{{\bar {x}}}^{{\alpha + \beta }}}} d\bar {x} = \frac{1}{{1 + \alpha + \beta }}, \\ \end{gathered} $Теперь можно найти требуемую массу профилированной балки, сравнив ее с прямоугольной
(33)
$m = \rho w\left( 1 \right)h\left( 1 \right)l{{\delta }_{V}} = \frac{{\rho {{w}_{0}}{{h}_{0}}l{{\delta }_{V}}}}{{{{\delta }_{U}}}} = {{m}_{0}}{{\delta }_{m}}.$Учитывая соотношение равнопрочности ${{\alpha }_{i}} = \gamma - 2{{\beta }_{i}}$, находим
(34)
${{\delta }_{{mi}}} = \frac{{{{\delta }_{{Vi}}}}}{{{{\delta }_{{Ui}}}}} = \frac{{1 + 2\gamma - {{\alpha }_{i}} - 3{{\beta }_{i}}}}{{\left( {1 + 2\gamma } \right)\left( {1 + {{\alpha }_{i}} + {{\beta }_{i}}} \right)}} = \frac{{1 + 2\gamma - \gamma - {{\beta }_{i}}}}{{\left( {1 + 2\gamma } \right)\left( {1 + \gamma - {{\beta }_{i}}} \right)}} = \frac{1}{{1 + 2\gamma }}.$Результат (34) означает постоянство коэффициента снижения массы любой равнопрочной балки с заданной упругой энергией для каждого вида нагружения: для концевой силы возможно снижение массы в три раза, для распределенной нагрузки – в пять, для линейно растущей от конца к корню – в семь раз. Сравнивая (34) с формулой (28), можно заключить, что изменение изгибающего момента в полукольце, пропорциональное синусу полярного угла, эквивалентно по снижению массы случаю степенного изменения момента в балке с показателем γ = 1/2, что соответствует изменению уровня распределенной нагрузки пропорционально ${{\bar {x}}^{{5/2}}}$.
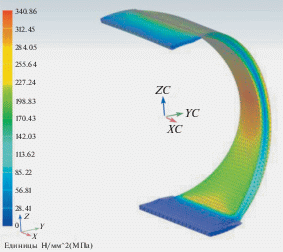
Компьютерное моделирование и МКЭ-расчеты равнопрочных колец и волнистых лент. Для уточнения расчетов перемещений и напряжений в нагруженных кольцах, профилированных полукольцах (рис. 6) и пружинах из волнистых лент (рис. 4) были построены соответствующие компьютерные 3-D модели и проведены расчеты методом конечных элементов (МКЭ). Результаты оказались в удовлетворительном согласии с аналитическими, упрощенными расчетами.
В качестве полезного инженерного приложения для автоматизированного проектного расчета ленточных пружин был написан “калькулятор” на языке Swift в интегрированной среде разработки XCode 9.3 для платформы программного обеспечения Apple IOS 11.4. Использовать его весьма просто и удобно. Приложение состоит из одного экрана, на котором в соответствии с техническими требованиями и характеристиками выбранного материала для пружины вводятся в текстовые поля следующие параметры: максимальная нагрузка; податливость; высота пружины; ширина ленты; число лент; предел прочности; модуль Юнга; коэффициенты формы. После ввода всех параметров и команды “рассчитать” на экране появятся необходимые число полуколец и значение толщины ленты, полученные из условий, заданных прочности и податливости.
4. Изготовление на 3-D принтере и испытания модельных образцов
Модельные образцы ленточных пружин, а также профилированных и обычных полуколец с одинаковыми размерами наиболее нагруженного сечения были изготовлены на 3-D принтере из стандартных (неармированных) пластиков. Масса полуколец – обычного и типа констэра была одинаковой, но за счет профилирования (при равной прочности) податливость полукольца констэра оказалась примерно на 70% выше, чем у аналогичного полукольца с постоянными размерами сечения, что удовлетворительно согласуется с результатами МКЭ-расчетов и с оценками по приближенной (балочной) формуле (28). Для изготовления реальных композитных образцов пружин из равнопрочных волнистых лент необходима отработка технологии 3-D печати композитных деталей с расположением по заданным траекториям пропитанных связующим жгутов волокон (рис. 7).
Приложение. Методы расчета плоских пружин различной геометрии. Для получения наглядных результатов, отражающих только влияние профилирования листов на податливость и несущую способность, в настоящей статье использовалось самое простое допущение о полукольцевой форме звена пружины из волнистых лент. При этом не рассматривалось влияние связи одного полукольца с соседним, а эта связь – из соображений симметрии – эквивалентна жесткому защемлению, т.е. запрещению поворота концов полуколец. При проектировании реальных пружин необходим более корректный учет их размеров и формы. В табл. 2 [8] приведены схемы нагружения практически применяемых звеньев ленточных пружин с соответствующими расчетными формулами для податливости и максимальных напряжений.
Таблица 2.
| Тип пружины | Прогиб пружины | Предельная нагрузка и максимальное напряжение | |||
|---|---|---|---|---|---|
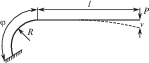 |
${{{v}}_{1}} = \frac{{KP{{R}^{3}}}}{{3EI}}{{\left( {\frac{l}{R} + \varphi } \right)}^{3}}$ Для нахождения K при α = φ |
Для 0 ≤ α ≤ 90 $P = \frac{{W\sigma }}{{l + R\sin \varphi }}$ $\sigma = \frac{{PR\left( {\frac{l}{R} + \sin \varphi } \right)}}{W}$ |
Для 90 ≤ α ≤ 180 $P = \frac{{W\sigma }}{{l + R}}$ $\sigma = \frac{{PR\left( {\frac{l}{R} + 1} \right)}}{W}$ |
||
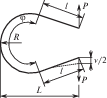 |
${{{v}}_{2}} = \frac{{2KP{{R}^{3}}}}{{3EI}}{{\left( {\frac{l}{R} + \frac{\varphi }{2}} \right)}^{3}}$ Для нахождения K при α = φ/2 |
$P = \frac{{W\sigma }}{L}$ | |||
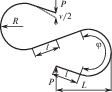 |
$\begin{gathered} {{{v}}_{3}} = 2{{{v}}_{2}} = \\ = \frac{{4KP{{R}^{3}}}}{{3EI}}{{\left( {\frac{l}{R} + \frac{\varphi }{2}} \right)}^{3}} \\ \end{gathered} $ Для нахождения K при α = φ/2 |
$\sigma = \frac{{PL}}{W}$ | |||
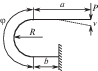 |
$\begin{gathered} {{{v}}_{4}} = {{{v}}_{5}} = ~ \\ = \frac{P}{{3EI}}\left[ {2K{{R}^{3}}{{{\left( {\frac{a}{R} + \frac{\varphi }{2}} \right)}}^{3}} + } \right. \\ \left. {^{{^{{^{{^{{}}}}}}}} + \;{{{\left( {b - a} \right)}}^{3}}} \right] \\ \end{gathered} $ Для нахождения K при α = φ/2 |
$P = \frac{{W\sigma }}{\lambda }$ | |||
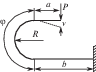 |
$\sigma = \frac{{P\lambda }}{W}$ | ||||
| Первый случай | Второй случай | λ-плечо силы | |||
| $a \geqslant b$ | – | $a + R$ | |||
| $a > b$ | $\begin{gathered} \left( {a - b} \right) < \hfill \\ < \left( {a + R} \right) \hfill \\ \end{gathered} $ | $a + R$ | |||
| $a < b$ | $\begin{gathered} \left( {b - a} \right) > \hfill \\ > \left( {a + R} \right) \hfill \\ \end{gathered} $ | $b - a$ | |||
| $a = 0$ | $b \leqslant R$ | $R$ | |||
| $a = 0$ | $b > R$ | $b$ | |||
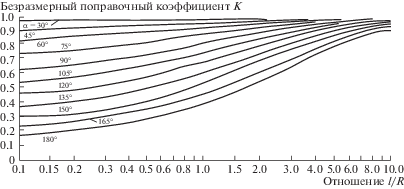
Поправочный коэффициент K для этих формул представлен в виде номограмм на рис. 8 и этот коэффициент зависит от отношения длины прямолинейного участка l к радиусу закругления пружины R, а также от полярного угла α круговой части пружины (табл. 2). Этот коэффициент K оказывает существенное влияние на точность расчетов прогибов ленточных пружин.
Рис. 8.
Зависимость поправочного коэффициента K от отношения длины прямолинейного участка l к радиусу закругления пружины R и от полярного угла круговой части пружин.
Выводы: 1. Ленточная пружина из волнистых стеклопластиковых лент может обеспечивать многократное снижение массы по сравнению со стальным аналогом при заданных несущей способности и накопленной упругой энергии. 2. Кассетная подвеска из разрезных стеклопластиковых колец обладает существенно нелинейной жесткостью, что положительно сказывается на обеспечении плавности движения транспортного средства. 3. Любая равнопрочная балка при заданных прочности и накопленной упругой энергии дает по сравнению с прямоугольной трехкратное снижение массы при нагружении концевой силой и пятикратное при равномерно распределенной нагрузке. Для изменения изгибающего момента по степенному закону $M(\bar {x})\sim {{\bar {x}}^{\gamma }}$ коэффициент снижения массы выражается простой формулой ${{\delta }_{m}} = {{(1 + 2\gamma )}^{{ - 1}}}$. 4. Равнопрочное профилирование диаметрально нагруженного кольца в идеальном случае приводит к двукратному снижению массы, что соответствует степенному закону изменения изгибающего момента с показателем $\gamma = 1{\text{/}}2$.
Список литературы
Полилов А.Н., Татусь Н.А., Шабалин В.В. Особенности проектирования упругих элементов в виде профилированных композитных балок // Проблемы машиностроения и надежности машин. 2011. № 6. С. 34. Polilov A.N., Tatus N.A., Shabalin V.V. Peculiarities of constructing elastic elements in the form of shaped composite beams // Journal of Machinery Manufacture and Reliability. 2011. V. 40. № 6. P. 532.
Полилов А.Н., Татусь Н.А., Плитов И.С. Оценка влияния разориентации волокон на жесткость и прочность профилированных композитных элементов // Проблемы машиностроения и надежности машин. 2013. № 5. С. 58. Polilov A.N., Tatus N.A., Plitov I.S. Estimating the effect of misorientation of fibers on stiffness and strength of profiled composite elements // Journal of Machinery Manufacture and Reliability. 2013. V. 42. № 5. P. 390.
Полилов А.Н., Татусь Н.А. Биомеханика прочности волокнистых композитов. ФизМатЛит. Москва. 2018. 328 с. ISBN: 978-5-9221-1760-9.
Кербер М.Л. Полимерные композиционные материалы. Структура. Свойства. Технологии. СПб.: Профессия, 2008. 560 с.
Васильев В.В. Механика конструкций из композиционных материалов. М.: Машиностроение, 1988. 272 с.
Карпинос Д.М. Композиционные материалы. Справочник. Киев: Наукова думка, 2007. 563 с.
Алфутов Н.А., Зиновьев П.А., Попов Б.Г. Расчет многослойных пластин и оболочек из композиционных материалов. М.: Машиностроение, 1984. 446 с.
Conklin R.M., Forry D.R. Design of flat-wound tension springs, Trans. AS ME 74, 5, 743–749, July 1952.
Goldsworthy W.B. 2012. Pulforming. In: Nicolais L., Borzacchiello A. (Eds.), Wiley Encyclopedia of Composites. John Wiley & Sons, Hoboken, NJ, ISBN: 978-0-470-12828-2, pp. 2542-2544. https://doi.org/10.1002/9781118097298.weoc209
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин