Проблемы машиностроения и надежности машин, 2020, № 4, стр. 35-43

В настоящее время при анализе напряженно-деформированного состояния (НДС) оболочек вращения чаще всего используется теория тонких оболочек, основанная на гипотезах Кирхгофа [1, 2]. При решении ряда задач (короткопролетные конструкции, оболочки с жестким защемлением и др.) необходимо учитывать деформации поперечного сдвига [3–5]. Учитывая, что решение систем дифференциальных уравнений, описывающих процессы деформирования тонких оболочек, аналитическими методами трудоемко, для анализа НДС оболочек и других типов конструкций в основном используются численные методы их расчета [6–13]. В широко распространенных конечно-элементных программных комплексах типа Nastran, Ansys, Abaqus и им подобных, используется неинвариантная интерполяция отдельных компонент вектора перемещения через узловые значения этих же компонент как скалярных величин, что приводит к получению некорректных результатов [8]. Поэтому задача создания усовершенствованных алгоритмов расчета оболочек вращения с учетом деформаций поперечного сдвига [4] на основе инвариантной интерполяционной процедуры является актуальной и представляет, как теоретический интерес, так и практическую значимость.

Определение НДС оболочек обычно выполняется на основе использования гипотезы о том, что любое волокно, нормальное к срединной поверхности в исходном состоянии, остается прямым и нормальным к срединной поверхности в ее деформированном состоянии. При таком подходе не учитываются деформации поперечного сдвига и соответствующие касательные напряжения, что может привести к значительным некорректностям при коротких пролетах оболочечных конструкций, а также в приопорных зонах граничных заделок.

При учете деформации поперечного сдвига нормаль к срединной поверхности в исходном состоянии при нагружении остается прямой линией, наклон которой определяется углами поворотов относительно координатных осей, касательных к срединной поверхности [5]. В настоящей статье угол наклоненной нормали определяется вектором γ [5], отсчет которого осуществляется в двух вариантах: от исходной нормали – в первом варианте отсчета; от нормали к деформированной срединной поверхности – во втором варианте.

При конечно-элементной реализации алгоритма учета поперечных сдвиговых деформаций реализована аппроксимация перемещений и угловых параметров как составляющих скалярных и векторных полей. Показана эффективность использования векторной аппроксимации искомых величин в четырехстороннем конечном элементе, являющимся фрагментом срединной поверхности оболочки вращения.

Геометрия оболочки вращения. Представление геометрии срединных поверхностей оболочек различных конфигураций с использованием радиус-векторов достаточно полно изложено в [14]. Радиус-вектор, задающий срединную поверхность оболочки вращения, может быть определен по формуле

где x – осевая координата; r = r(x) – радиус вращения; θ – угол, отсчитываемый от оси OZ против хода часовой стрелки.

Дифференцированием (1) по криволинейным координатам s, θ можно определить базисные векторы произвольной точки срединой поверхности ${{\{ {{{\mathbf{e}}}^{0}}\} }^{T}}$ = $\{ {\mathbf{e}}_{1}^{0}{\mathbf{e}}_{2}^{0}{\mathbf{e}}_{n}^{0}\} $ и их производные $\{ {\mathbf{e}}_{{,\alpha }}^{0}\} $ = $[{{m}_{\alpha }}]\{ {{{\mathbf{e}}}^{0}}\} $, ${{\{ {\mathbf{e}}_{{,\alpha }}^{0}\} }^{T}}$ = $\{ {\mathbf{e}}_{{1,\alpha }}^{0}{\mathbf{e}}_{{2,\alpha }}^{0}{\mathbf{e}}_{{n,\alpha }}^{0}\} $.

Вектор перемещения точки срединной поверхности оболочки вращения и вектор углов поворота, а также их производные по криволинейным координатам s₁ и s₂, можно представить компонентами, отнесенными к базису этой же точки

где ${{{v}}^{\rho }}$, $~{v}$ – компоненты вектора перемещения и ${{\gamma }^{\rho }}$, ${{\gamma }^{3}}$ – вектора углов поворота.

Положение точки, отстоящей от срединной поверхности на расстоянии ζ до и после деформирования, определяется соответствующими радиус-векторами

Входящий в (3) вектор перемещения точки, отстоящей от срединной поверхности на расстоянии ζ, можно определить по формуле

где $\gamma = {{{\gamma }}^{1}}{\mathbf{e}}_{1}^{0} + {{{\gamma }}^{2}}{\mathbf{e}}_{2}^{0} + {{{\gamma }}^{3}}{\mathbf{e}}_{n}^{0}$ – вектор углов поворота.

Компоненты ${{{\gamma }}^{1}}$, ${{{\gamma }}^{2}}$ представляют собой повороты нормали вокруг тангенциальных базисных векторов. Компонента γ характеризует средний поворот всей окрестности рассматриваемой точки срединной поверхности вокруг нормали [5].

Формула (4) соответствует варианту отсчета угла поворота от нормали исходного состояния. Данный подход предложен в [4, 5]. Если же отсчет угла поворота осуществлять от перпендикуляра к срединной поверхности в деформированном состоянии, то соотношение (4) примет вид

где $\Delta {\mathbf{e}} = \Delta {{e}^{1}}{\mathbf{e}}_{1}^{0} + \Delta {{e}^{2}}{\mathbf{e}}_{2}^{0} + \Delta {{e}^{3}}{\mathbf{e}}_{n}^{0}$ – разность ортов нормалей в деформированном и исходном состояниях.

Ковариантные компоненты тензора деформаций определяются соотношением механики сплошной среды [15] и могут быть представлены в матричном виде

где $\mathop {{{{\{ \varepsilon \} }}^{T}}}\limits_{5 \times 1} = \{ \varepsilon _{{11}}^{\zeta }\varepsilon _{{22}}^{\zeta }{\text{2}}\varepsilon _{{12}}^{\zeta }{\text{2}}\varepsilon _{{13}}^{\zeta }{\text{2}}\varepsilon _{{23}}^{\zeta }\} $ – матрица-строка ковариантных компонент тензора деформаций; $\mathop {{{{\{ U\} }}^{T}}}\limits_{6 \times 1} $ = $\{ {{{v}}^{1}}{{{v}}^{2}}{v}{{\gamma }^{1}}{{\gamma }^{2}}{{\gamma }^{3}}\} $ – матрица-строка линейных и угловых параметров; [N] – матрица алгебраических и дифференциальных операторов.

Конечный элемент и интерполяция перемещений. В качестве элемента дискретизации выбирается четырехугольный фрагмент срединной поверхности оболочки вращения с узлами i, j, k, l, отображаемый на квадрат с локальной системой координат –1 ≤ ξ, η ≤ 1. Столбец узловых неизвестных в глобальной и локальной системах координат выбирается в виде

где $\mathop {{{{\{ q_{y}^{{\text{г}}}\} }}^{T}}}\limits_{1 \times 12~~~~} $ = $\{ {{q}^{i}}{{q}^{j}}{{q}^{k}}{{q}^{l}}q_{{,1}}^{i}q_{{,1}}^{j}q_{{,1}}^{k}q_{{,1}}^{l}q_{{,2}}^{i}q_{{,2}}^{j}q_{{,2}}^{k}q_{{,2}}^{l}\} $; Здесь под q понимается компонента вектора перемещения ${{{v}}^{1}}$, ${{{v}}^{2}}$ или ${v}$.

При использовании общепринятой в настоящее время в МКЭ неинвариантной интерполяции отдельных компонент вектора перемещения как скалярных величин [4, 6, 11–13] применяются интерполяционные выражения следующего вида

где $\mathop {{{{\{ \psi \} }}^{T}}}\limits_{1 \times 12~~~~} = \{ {{\psi }_{1}}{{\psi }_{2}} \ldots {{\psi }_{{12}}}\} $; $\mathop {{{{\{ \varphi \} }}^{T}}}\limits_{1 \times 4~~~~} = \{ {{\varphi }_{1}}{{\varphi }_{2}}{{\varphi }_{3}}{{\varphi }_{4}}\} $ – функции формы, представляющие собой произведения полиномов Эрмита третьей степени и билинейные функции локальных координат соответственно.

Как видно в аппроксимирующих функциях (9) каждая искомая величина внутренней точки конечного элемента выражается через узловые значения только этой же величины.

На основе соотношений (9) формируется аппроксимирующее выражение в матричном виде

Применение интерполяционных выражений (9) позволяет получать корректные решения только в декартовой системе координат. Использование данных зависимостей в криволинейных координатах может приводить к существенным погрешностям вычислений, особенно при значительных кривизнах срединных поверхностей оболочек или при наличии возможности смещения оболочки под действием заданной нагрузки как абсолютно твердого тела. Поэтому наиболее адекватным является применение инвариантной векторной интерполяционной процедуры, основанной на использовании выражений вида

где $\mathop {{{{\{ {\mathbf{v}}_{y}^{{\text{л}}}\} }}^{T}}}\limits_{~1 \times 12~~~~} $ = $\{ {{{\mathbf{v}}}^{i}}{{{\mathbf{v}}}^{j}}{{{\mathbf{v}}}^{k}}{{{\mathbf{v}}}^{l}}{\mathbf{v}}_{{,{\xi }}}^{i}{\mathbf{v}}_{{,{\xi }}}^{j}{\mathbf{v}}_{{,{\xi }}}^{k}{\mathbf{v}}_{{,{\xi }}}^{l}{\mathbf{v}}_{{,{\eta }}}^{i}{\mathbf{v}}_{{,{\eta }}}^{j}{\mathbf{v}}_{{,{\eta }}}^{k}{\mathbf{v}}_{{,{\eta }}}^{l}\} $; $\mathop {{{{\{ {{\gamma }_{у}}\} }}^{T}}}\limits_{~1 \times 4~~~~} $ = $\{ {{\gamma }^{i}}{{\gamma }^{j}}{{\gamma }^{k}}{{\gamma }^{l}}\} $; $\mathop {{{{\{ {\mathbf{v}}_{y}^{{\text{г}}}\} }}^{T}}}\limits_{~1 \times 12~~~~} $ = = $\{ {{{\mathbf{v}}}^{i}}{{{\mathbf{v}}}^{j}}{{{\mathbf{v}}}^{k}}{{{\mathbf{v}}}^{l}}{\mathbf{v}}_{{,1}}^{i}{\mathbf{v}}_{{,1}}^{j}{\mathbf{v}}_{{,1}}^{k}{\mathbf{v}}_{{,1}}^{l}{\mathbf{v}}_{{,2}}^{i}{\mathbf{v}}_{{,2}}^{j}{\mathbf{v}}_{{,2}}^{k}{\mathbf{v}}_{{,2}}^{l}\} $ – матрицы-строки векторных узловых неизвестных; [L] – матрица перехода от столбца $\{ {\mathbf{v}}_{y}^{{\text{л}}}\} $ к столбцу $\{ {\mathbf{v}}_{y}^{{\text{г}}}\} $; $\mathop {[{{{\mathbf{A}}}_{{\gamma }}}]}\limits_{~4 \times 12~} $, $\mathop {[{{{\mathbf{A}}}_{{v}}}]}\limits_{~12 \times 36~} $ – матрицы, элементами которых являются строки базисных векторов узловых точек.

Производные векторов ${\mathbf{v}}$ и γ определяются дифференцированием выражений (11) и (12)

Входящие в структуру матриц $[{{{\mathbf{A}}}_{{v}}}]$ и $[{{{\mathbf{A}}}_{\gamma }}]$ векторы базисов узлов КЭ могут быть выражены через векторы локального базиса внутренней точки четырехугольного КЭ

где $\{ {{{\mathbf{e}}}^{{o\rho }}}\} = \{ {\mathbf{e}}_{1}^{{o\rho }}{\mathbf{e}}_{2}^{{o\rho }}{\mathbf{e}}_{n}^{{o\rho }}\} $; верхний индекс ${\rho }$ обозначает узел КЭ i, j, k или l.

Представляя левые части (11), (12) и (13) выражениями (2), можно получить соотношения

Приравнивая соответствующие выражения при ${{\{ {{e}^{0}}\} }^{T}}$ в левых и правых частях равенств (15), можно получить искомые аппроксимирующие зависимости для компонент вектора перемещения и компонент вектора углов поворота, а также их производных

На основании (16) можно сформулировать матричное соотношение

Анализируя (16), можно отметить их принципиальное отличие от (9), которое заключается в том, что при использовании инвариантной векторной интерполяционной процедуры каждая компонента вектора перемещения зависит от узловых значений всех трех компонент векторов перемещений и их производных, а каждая компонента вектора угла поворота нормали зависит от узловых значений всех компонент векторов углов поворота нормалей узлов КЭ. При использовании общепринятой интерполяции отдельных компонент вектора перемещения и компонент вектора угла поворота как скалярных величин, каждая компонента вектора перемещения зависит от узловых значений этой же компоненты и не зависит от узловых значений остальных двух компонент и их производных, а каждая компонента вектора угла поворота зависит от узловых значений только этой же компоненты и не зависит от узловых значений остальных компонент.

Аппроксимации искомых величин (10) и (17) можно представить в матричном виде

$\mathop {[{{D}_{w}}]}\limits_{~6 \times 48~} $ – матрица аппроксимирующих функций по (10) или (17).

С использованием аппроксимирующих выражений (18) стандартным образом формируется матрица жесткости конечного элемента [K]

где $\mathop {{{{\{ {{F}_{y}}\} }}^{T}}}\limits_{~1 \times 48~} = \left\{ {\mathop {{{{\{ {{f}_{y}}\} }}^{T}}}\limits_{~1 \times 36~} \mathop {{{{\{ 0\} }}^{T}}}\limits_{~1 \times 12~} } \right\}$ – матрица-строка узловых усилий конечного элемента.

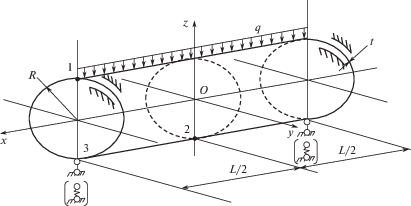
Пример расчета. Была решена задача по определению НДС цилиндра, загруженного вдоль образующей равномерно распределенной нагрузкой интенсивности q и имеющего по торцам шарнирные опоры, препятствующие вертикальному смещению (рис. 1).

Вдоль торцевых окружностей цилиндра запрещена производная нормальной компоненты вектора перемещения, т.е. торцы цилиндра имеют скользящую заделку. Были приняты следующие исходные данные: q = 0.25 H/см; L = 40 см; R = 40 см; t = 0.4 см; E = 2 × 10⁷ Н/см²; $v$ = 0.3. Вследствие наличия плоскостей симметрии рассчитана 1/4 часть цилиндра. Расчеты выполнены в двух вариантах отсчета угла поворота как при векторной, так и при скалярной интерполяционных процедурах.

Результаты повариантного расчета представлены в табл. 1, в которой приведены значения нормальных и сдвиговых напряжений на внутренней σ^вн и наружной σ^н поверхностях цилиндра в точках 1 и 2 (рис. 1) в зависимости от вида интерполяционной процедуры и сетки узлов дискретизации рассчитываемого фрагмента.

Анализ численных значений напряжений, представленных в табл. 1, показывает, что в обоих вариантах расчета наблюдается удовлетворительная сходимость вычислительного процесса как при скалярной, так и при векторной интерполяционных процедурах. Однако, во втором варианте расчета нормальные напряжения имеют значения, превышающие значения нормальных напряжений первого варианта примерно на 10%. Напряжения сдвига, наоборот, во втором варианте имеют меньшие значения (примерно в 2 раза) по сравнению с первым вариантом. Результаты второго варианта расчета являются более корректными из-за более полного использования дифференциальных характеристик параметров деформированного состояния. Если шарнирные опоры, препятствующие вертикальному смещению цилиндра, заменить на пружинные, то оболочка получит возможность смещаться вертикально вниз как абсолютно твердое тело. Варьируя жесткостью пружины, можно получать различные величины жесткого смещения.

Результаты повариантного расчета при изменении условий опирания представлены в табл. 2 (скалярная интерполяционная процедура) и в табл. 3 (векторная интерполяционная процедура), в которых приведены значения напряжений при сетке узлов 21 × 21 в точках 1 и 3 с различными значениями жесткого смещения цилиндра.

Вывод. Анализ полученных данных показывает, что при использовании скалярной интерполяционной процедуры численные значения напряжений при жестком смещении оболочки существенно изменяются (сильно возрастают), достигая неприемлемых значений. При использовании векторной интерполяционной процедуры в обоих вариантах расчета НДС цилиндра не меняется, несмотря на существенную величину жесткого смещения, т.к. использование векторной аппроксимации позволяет в неявном виде автоматически учитывать смещения конечного элемента как жесткого целого при использовании криволинейной системы координат. Таким образом, на основании численных расчетов, можно сделать вывод, что в задачах по определению НДС оболочек вращения с учетом сдвиговых деформаций необходимо использовать именно векторную интерполяцию линейных и угловых искомых величин.