Проблемы машиностроения и надежности машин, 2020, № 4, стр. 44-50

ИССЛЕДОВАНИЕ САМОТОРМОЗЯЩИХСЯ ПЛАНЕТАРНЫХ ПЕРЕДАЧ С ОДНОВЕНЦОВЫМИ САТЕЛЛИТАМИ

Г. А. Тимофеев^1, *, В. В. Панюхин¹, Д. В. Сащенко¹

¹ Московский государственный технический университет им. Н.Э. Баумана
Москва, Россия

Поступила в редакцию 07.02.2019
Принята к публикации 07.03.2020

DOI: 10.31857/S0235711920040148

Аннотация

Изложены результаты исследования самоторможения планетарных передач с одновенцовыми сателлитами, центральными и опорными колесами, имеющими внеполюсные зацепления. С помощью разработанного метода исследования самоторможения механизмов определены условия самоторможения этих планетарных передач. Найдены области существования самотормозящихся зацеплений, где они имеют высокий КПД прямого хода.

Ключевые слова: условия самоторможения, самотормозящиеся планетарные передачи с одновенцовыми сателлитами, области существования самотормозящихся внеполюсных зацеплений, высокий КПД прямого хода планетарных самотормозящихся зубчатых передач

Реализация самоторможения в планетарных передачах (механизмах) без применения специальных тормозящих устройств в робототехнике и грузоподъемной технике является актуальной. Для этого необходимо использовать внутренние и внешние зацепления со значительными смещениями.

Задачей настоящего исследования является синтез высокоэффективных конструкций самотормозящихся планетарных передач, содержащих внеполюсные зацепления тормозящих профилей. Синтез предусматривает выделение в области существования планетарной передачи подобласти самоторможения и поиск в этой подобласти оптимальных параметров конструкции.

Имеющиеся в литературе [1–8] сведения о наличии или отсутствии самоторможения в планетарных передачах получены на основе анализа передач с зацеплениями, имеющими одинаковые значения КПД прямого и обратного хода. Поэтому они характеризуют только тот частный случай, когда все зацепления имеют центральное расположение полюса на линии зацепления. Известно, что во внеполюсных цилиндрических зацеплениях можно получить такую разницу между КПД прямого и обратного хода, которая обеспечивает самоторможение при обратном ходе при достаточно высоком значении КПД прямого хода [9].

Проведенное исследование цилиндрических передач внешнего и внутреннего зацепления показало, что для достижения в них самоторможения нужно использовать зацепления со значительным смещением [7, 8]. Поскольку в прямозубых зацеплениях возможности смещения рабочих участков профилей очень ограничены из-за опасности заострения или подрезания зубьев, в необходимых случаях они заменяются косозубыми или шевронными, для которых допустимые смещения значительно больше. В косозубых передачах величина смещения рабочих участков профилей от полюса определяется в основном разницей углов наклона профилей зубьев, участвующих в зацеплении. Поэтому задача обеспечения самоторможения планетарной передачи в заданном состоянии сводится к определению необходимых для этого углов наклона зубьев во внеполюсных зацеплениях. При этом нормальные углы профилей выбираются из тех же соображений, что и в обычных передачах.

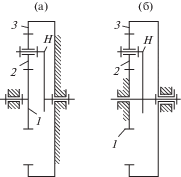
Схемы одновенцовых планетарных передач по классификации В.Н. Кудрявцева [1, 12] имеют обозначения: $A_{{H1}}^{3}$, $A_{{H3}}^{1}$ (рис. 1). Кинематическая схема передачи $A_{{H1}}^{3}$ с одновенцовым сателлитом 2, имеющим внешнее зацепление с центральным колесом 3, представлена на рис. 1а. Кинематическая схема планетарной передачи $A_{{H3}}^{1}$ с одновенцовым сателлитом 2, имеющим внутреннее зацепление с центральным колесом 3, представлена на рис. 1б.

Рис. 1.

Схемы планетарных передач: (а) – $A_{{H1}}^{3}$; (б) – $A_{{H3}}^{1}$.

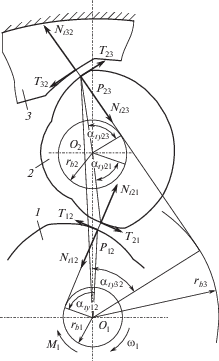
Схема сил в зацеплениях показана на рис. 2. Силы, действующие на водило Н и само водило на рис. 2 не показаны.

Рис. 2.

Силовая схема планетарной передачи $A_{{H1}}^{3}$.

Запишем уравнения равновесия центрального колеса 1, сателлита 2 и водила Н при установившемся движении в тяговом режиме прямого хода, когда ведущим является колесо 1, а ведомым – водило Н

(1)

${{M}_{1}} = {{r}_{{b1}}}\left( {{{N}_{{t12}}} + {{T}_{{12}}}\operatorname{tg} {{\alpha }_{{ty12}}}} \right),$

(2)

${{r}_{{b2}}}\left( {{{N}_{{t21}}} + {{T}_{{21}}}\operatorname{tg} {{\alpha }_{{ty21}}}} \right) = {{r}_{{b2}}}\left( {{{N}_{{t23}}} + {{T}_{{23}}}\operatorname{tg} {{\alpha }_{{ty23}}}} \right),$

(3)

$\begin{gathered} {{M}_{H}} = {{T}_{{21}}}\left( {{{r}_{{b1}}}\operatorname{tg} {{\alpha }_{{ty12}}} + {{r}_{{b2}}}\operatorname{tg} {{\alpha }_{{ty21}}}} \right) + {{N}_{{t21}}}\left( {{{r}_{{b1}}} + {{r}_{{b2}}}} \right) + \\ + \;{{N}_{{t23}}}\left( {{{r}_{{b3}}} - {{r}_{{b2}}}} \right) + {{T}_{{23}}}\left( {{{r}_{{b3}}}\operatorname{tg} {{\alpha }_{{ty32}}} - {{r}_{{b2}}}\operatorname{tg} {{\alpha }_{{ty23}}}} \right). \\ \end{gathered} $

Преобразуем уравнения (1)–(3) к виду

(4)

${{M}_{1}} = {{N}_{{t12}}}{{r}_{{b1}}}\left( {1 + {{\tau }_{{12}}}} \right),$

(5)

${{N}_{{t21}}}\left( {1 + {{\tau }_{{21}}}} \right) = {{N}_{{t23}}}\left( {1 + {{\tau }_{{23}}}} \right),$

(6)

${{M}_{H}} = {{N}_{{t21}}}\left[ {{{r}_{{b1}}}\left( {1 + {{\tau }_{{12}}}} \right) + {{r}_{{b2}}}\left( {1 + {{\tau }_{{21}}}} \right)} \right] + {{N}_{{t23}}}\left[ {{{r}_{{b3}}}\left( {1 + {{\tau }_{{32}}}} \right) - {{r}_{{b2}}}\left( {1 + {{\tau }_{{23}}}} \right)} \right],$

(7)

${\text{где}}\quad {{\tau }_{{ij}}} = \frac{{{{T}_{{ij}}}\operatorname{tg} {{\alpha }_{{tij}}}}}{{{{N}_{{tij}}}}};\quad i,j = {\text{ }}1,2,3.$

Если силы трения T_ij пропорциональны нормальным реакциям N_ij, то параметры торможения τ_ij принимают вид

(8)

${{\tau }_{{ij}}} = \frac{{{{f}_{{ij}}}\operatorname{tg} {{\alpha }_{{tij}}}}}{{\cos {{\beta }_{b}}}};\quad i,j = 1,2,3.$

Решая систему уравнений (4)–(6), найдем отношение выходного M_H и входного M₁ моментов

(9)

$\frac{{{{M}_{H}}}}{{{{M}_{1}}}} = 1 + \frac{{{{r}_{{b3}}}(1 + {{\tau }_{{21}}})(1 + {{\tau }_{{32}}})}}{{{{r}_{{b1}}}(1 + {{\tau }_{{12}}})(1 + {{\tau }_{{23}}})}} = 1 + \frac{{{{r}_{{b3}}}}}{{{{r}_{{b1}}}}}{{\eta }_{{12}}}{{\eta }_{{23}}}.$

Умножая на передаточное отношение и учитывая, что радиусы основных окружностей пропорциональны числам зубьев, получаем известную [11] формулу для КПД прямого хода

(10)

${{\eta }_{{1H}}} = \left( {1 + \frac{{{{z}_{3}}}}{{{{z}_{1}}}}{{\eta }_{{23}}}{{\eta }_{{12}}}} \right):\left( {1 + \frac{{{{z}_{3}}}}{{{{z}_{1}}}}} \right).$

Из уравнений (4)–(6) и (10) следует, что тяговый режим прямого хода передачи $A_{{H1}}^{3}$ возможен при одновременном выполнении условий

(11)

$ - \frac{{{{z}_{1}}}}{{{{z}_{3}}}} < {{\eta }_{{23}}}{{\eta }_{{12}}} < 1;\quad {{\tau }_{{12}}} > --{\text{ }}1;\quad {{\tau }_{{21}}} > --{\text{ }}1;\quad {{\tau }_{{23}}} > --{\text{ }}1.$

Выполнение условий (11) практически не накладывает каких-либо дополнительных ограничений при проектировании передачи, поскольку при реальных значениях коэффициентов трения в зацеплениях эти условия не будут выполняться только для колес с очень большими углами наклона зубьев (более 80°).

Уравнения равновесия звеньев в тяговом режиме обратного хода, когда водило Н становится ведущим, отличаются от уравнений (1)–(3) противоположными знаками сил трения

(12)

${{M}_{1}} = {{r}_{{b1}}}\left( {{{N}_{{t12}}} - {{T}_{{12}}}\operatorname{tg} {{\alpha }_{{ty12}}}} \right),$

(13)

${{r}_{{b2}}}\left( {{{N}_{{t21}}} - {{T}_{{21}}}\operatorname{tg} {{\alpha }_{{ty21}}}} \right) = {{r}_{{b2}}}\left( {{{N}_{{t23}}} - {{T}_{{23}}}\operatorname{tg} {{\alpha }_{{ty23}}}} \right),$

(14)

$\begin{gathered} {{M}_{H}} = {{N}_{{t21}}}\left( {{{r}_{{b1}}} + {{r}_{{b2}}}} \right) - {{T}_{{21}}}\left( {{{r}_{{b1}}}\operatorname{tg} {{\alpha }_{{ty12}}} + {{r}_{{b2}}}\operatorname{tg} {{\alpha }_{{ty21}}}} \right) + \\ + \;{{N}_{{t23}}}\left( {{{r}_{{b3}}} - {{r}_{{b2}}}} \right) - {{T}_{{23}}}\left( {{{r}_{{b3}}}\operatorname{tg} {{\alpha }_{{ty32}}} - {{r}_{{b2}}}\operatorname{tg} {{\alpha }_{{ty23}}}} \right). \\ \end{gathered} $

Вводя обозначения по формуле (7), преобразуем уравнения (12)–(14) к виду

(15)

${{M}_{1}} = {{N}_{{t12}}}{{r}_{{b1}}}\left( {1 - {{\tau }_{{12}}}} \right),$

(16)

${{N}_{{t21}}}\left( {1 - {{\tau }_{{21}}}} \right) = {{N}_{{t23}}}\left( {1 - {{\tau }_{{23}}}} \right),$

(17)

${{M}_{H}} = {{N}_{{t21}}}\left[ {{{r}_{{b1}}}\left( {1 - {{\tau }_{{12}}}} \right) + {{r}_{{b2}}}\left( {1 - {{\tau }_{{21}}}} \right)} \right] + {{N}_{{t23}}}\left[ {{{r}_{{b3}}}\left( {1 - {{\tau }_{{32}}}} \right) - {{r}_{{b2}}}\left( {1 - {{\tau }_{{23}}}} \right)} \right].$

Решая систему уравнений (15)–(17), найдем отношение выходного и входного моментов

(18)

$\frac{{{{M}_{H}}}}{{{{M}_{1}}}} = 1 + \frac{{{{r}_{{b3}}}(1 - {{\tau }_{{21}}})(1 - {{\tau }_{{32}}})}}{{{{r}_{{b1}}}(1 - {{\tau }_{{12}}})(1 - {{\tau }_{{23}}})}} = 1 + \frac{{{{r}_{{b3}}}}}{{{{r}_{{b1}}}}}{{\eta }_{{32}}}{{\eta }_{{21}}}.$

Умножая на передаточное отношение и учитывая, что радиусы основных окружностей пропорциональны числам зубьев, получаем формулу для КПД обратного хода η_Н1

(19)

${{\eta }_{{H1}}} = \left( {1 + \frac{{{{z}_{3}}}}{{{{z}_{1}}}}} \right):\left( {1 + \frac{{{{z}_{3}}}}{{{{z}_{1}}{{\eta }_{{21}}}{{\eta }_{{32}}}}}} \right).$

В формулу (19) входят КПД η₂₁ и η₃₂ обратного хода отдельных зацеплений, а не прямого. Поскольку КПД обратного хода может значительно отличаться от КПД прямого хода, особенно во внеполюсных зацеплениях, это обстоятельство является существенным.

Из уравнений (15)–(17) и (19) следует, что при выполнении заполюсным зацепления колес 1, 2 условия самоторможения передачи при сохранении способности работы в режиме оттормаживания имеют вид

(20)

$ - \frac{{{{z}_{3}}}}{{{{z}_{1}}{{\eta }_{{32}}}}} < {{\eta }_{{21}}} < 0.$

Второе условие совпадает с тем, на основе которого получены выражения для определения углов β_у1 и β_у2 наклона зубьев колес самотормозящейся цилиндрической передачи

(21)

$\cos {{\beta }_{{y1}}} \leqslant \operatorname{tg} {{\alpha }_{{ny1}}}\sqrt {\sqrt {\frac{1}{4} + {{{\left[ {\frac{{\min f}}{{(1 - \min {{\psi }_{1}})\sin {{\alpha }_{{ny1}}}}}} \right]}}^{2}}} - \frac{1}{2}} ,$

(22)

$\cos {{\beta }_{{y2}}} > \operatorname{tg} {{\alpha }_{{ny2}}}\sqrt {\sqrt {\frac{1}{4} + {{{\left[ {\frac{{\max f}}{{(1 + \min {{\psi }_{2}})\sin {{\alpha }_{{ny2}}}}}} \right]}}^{2}}} - \frac{1}{2}} ,$

где ψ₁ и ψ₂ – коэффициенты, учитывающие трение качения и верчения в зацеплении и трение в опорах [4]

(23)

${{\psi }_{{1,2}}} = \frac{{{{M}_{K}}\cos {{\beta }_{b}} + {{M}_{В}}\sin {{\beta }_{b}} + {{M}_{{T1,2}}}}}{{{{М}_{{1,2}}}}},$

где М_K и М_В – моменты трения качения и верчения в зацеплении; М_Т и М – моменты трения в опорах и нормальной реакции.

Первое из условий (20), ограничивающих значение η₂₁, выразим через параметры τ₁₂ и τ₂₁, учитывающие трение скольжения в зацеплении, и коэффициенты ψ₁ и ψ₂

(24)

${{\eta }_{{21}}} = \frac{{1 - {{\tau }_{{12}}} - \min {{\psi }_{1}}}}{{1 - {{\tau }_{{21}}} + \min {{\psi }_{2}}}} > - \frac{{{{z}_{3}}}}{{{{z}_{1}}{{\eta }_{{32}}}}}.$

Параметры τ₁₂ и τ₂₁ можно выразить через коэффициент трения скольжения f₁₂ в зацеплении колес 1 и 2 и нормальные α_ny1 и α_ny2 углы профилей колес 1 и 2

(25)

${{\tau }_{{ij}}} = \frac{{{{f}_{{ij}}}\operatorname{tg} {{\alpha }_{{nyi}}}}}{{\cos {{\beta }_{{yi}}}\cos {{\beta }_{b}}}};\quad i,j = 1,2.$

Анализ условий (25) показывает, что оно ограничивает максимально допустимое значение параметра τ₁₂

(26)

$\max {{\tau }_{{12}}} < \frac{{{{z}_{3}}}}{{{{z}_{1}}{{\eta }_{{32}}}}}\left( {1 - \max {{\tau }_{{21}}} + \min {{\psi }_{2}}} \right) + 1 - \max {{\psi }_{1}}.$

Таким образом, в отличие от (21), найденное значение β_у1 должно удовлетворять условию

(27)

$\sec {{\beta }_{{y1}}} < \frac{{\cos {{\beta }_{b}}}}{{\max {{f}_{{12}}}\operatorname{tg} {{\alpha }_{{ny1}}}}}\left[ {\frac{{{{z}_{3}}}}{{{{z}_{1}}{{\eta }_{{32}}}}}\left( {1 - \max {{\tau }_{{21}}} + \min {{\psi }_{2}}} \right) + 1 - \max {{\psi }_{1}}} \right].$

Уравнения равновесия звеньев в режиме оттормаживания отличаются от (15)–(17) только знаком входного момента М₁. Их решение дает соотношение между выходным и входным моментами

(28)

$\frac{{{{M}_{H}}}}{{{{M}_{1}}}} = \frac{{{{r}_{{b3}}}(1 - {{\tau }_{{21}}})(1 - {{\tau }_{{32}}})}}{{{{r}_{{b1}}}(1 - {{\tau }_{{12}}})(1 - {{\tau }_{{23}}})}} - 1 = - \frac{{{{z}_{3}}}}{{{{z}_{1}}{{\eta }_{{32}}}{{\eta }_{{21}}}}} - 1.$

В том случае, когда режим оттормаживания необходимо исключить, и механизм предназначен для работы только в тяговом режиме прямого хода, параметры тормозящих профилей должны удовлетворять условиям

(29)

$\cos {{\beta }_{{y1}}} \leqslant \operatorname{tg} {{\alpha }_{{ny1}}}\sqrt {\sqrt {\frac{1}{4} + {{{\left[ {\frac{{\min f_{{12}}^{{}}}}{{(1 - \min {{\psi }_{1}})\sin {{\alpha }_{{ny1}}}}}} \right]}}^{2}}} - \frac{1}{2}} ,$

(30)

$\cos {{\beta }_{{y2}}} \leqslant \operatorname{tg} {{\alpha }_{{ny2}}}\sqrt {\sqrt {\frac{1}{4} + {{{\left[ {\frac{{\max f_{{12}}^{{}}}}{{(1 + \max {{\psi }_{2}})\sin {{\alpha }_{{ny2}}}}}} \right]}}^{2}}} - \frac{1}{2}} .$

При этом должно быть сохранено условие внеполюсности зацеплений

(31)

${{\beta }_{{y1}}} > {{\beta }_{{y2}}} > {{\beta }_{{y3}}}.$

Проведенный анализ показывает, что передача $A_{{H1}}^{3}$ может быть самотормозящейся при обратном ходе при сохранении высокого значения КПД прямого хода.

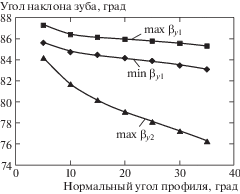
На рис. 3 показаны графики углов наклона колес самотормозящейся передачи от угла исходного профиля, построенные по формулам (21) и (27). Зона существования первого варианта самоторможения – полоса между графиками min β_y1 и max β_y1 (два верхних графика) для угла наклона колеса 1 и область ниже графика max β_y2 для угла наклона сателлита 2. Зона существования второго варианта самоторможения – область выше графика minβ_y1 для угла наклона колеса 1 и область выше графика maxβ_y2 для угла наклона сателлита 2.

Рис. 3.

Область самоторможения планетарной передачи $A_{{H1}}^{3}$.

Исследование для передачи $A_{{H3}}^{1}$ показало, что вид областей существования первого и второго вариантов самоторможения аналогичен приведенному на рис. 3.

Выводы. 1. Для самоторможения в отдельной ступени в составе планетарной передачи образующая ступень высшая кинематическая пара выполняется с таким смещением рабочего участка линии зацепления относительно полюса, которое обеспечивает снижение КПД обратного хода на величину, достаточную для самоторможения в целом. При этом смещение производится в том направлении, которое обеспечивает наибольший КПД прямого хода самотормозящейся передачи.

2. Планетарная передача с одновенцовыми сателлитами $A_{{H1}}^{3}$ может быть самотормозящейся при обратном ходе с возможностью оттормаживания либо без такового при сохранении высокого КПД прямого хода.

Список литературы

Планетарные передачи / Справочник. Под ред. В.Н. Кудрявцева и Ю.Н. Кирдяшева. Л.: Машиностроение, 1977. 536 с.
Крайнев А.Ф. Словарь-справочник по механизмам. М.: Машиностроение, 1981. 438 с.
Вейц В.Л. Динамика машинных агрегатов. Л.: Машиностроение, 1969. 370 с.
Турпаев А.И. Винтовые механизмы и передачи. М.: Машиностроение, 1982. 223 с.
Pennock G.R., Alwerdt J.J Duality between the kinematics of gear trains and the statistics of beam systems // Mech. Msch. Theory. 2007. V. 42 (11). P. 512–526.
Shigley J.E., Mischke C.R. Mechanical Engineering Design. 6^th ed. Boston: McGraw-Hill, 2001.
Litvin F.L. Development of Gear Technology and Theory of Gearing, NASA Ref. 1406, Lewis Research Center, Cleveland, OH, 1997.
Dooner D.B., Seireg A.A. The Kinematic Theory of Gearing. Jhon Wiley & Sons. New York, 1995.
Пат. 1479765 РФ, МКИ F 16 H 1/18. Цилиндрическая зубчатая передача / В.В. Панюхин (РФ). № 4336734/25-28. Опубл. 15.05.89. Бюл. № 18 // Открытия. Изобретения. 1989. № 18. С. 156.
Тимофеев Г.А., Панюхин В.В. Анализ критериев самоторможения // Вестник Машиностроения, 2002. № 9. С. 3.
Тимофеев Г.А., Самойлова М.В., Панюхин В.В. Анализ критериев самоторможения с точки зрения их обоснованности // Вестник Московского государственного технического университета им. Н.Э. Баумана. Серия: Машиностроение. 2013. № 4 (93). С. 27.
Кудрявцев В.Н. Планетарные передачи. М.-Л.: Машиностроение, 1966. 306 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал