Проблемы машиностроения и надежности машин, 2020, № 4, стр. 3-10

Манипуляционную систему двурукого робота можно рассматривать как механизм относительного манипулирования с большим числом степеней свободы. Механизм относительного манипулирования широко применяется в технологических системах при обработке поверхностей и реализации заданных относительных траекторий инструмента на подвижной детали. При этом используются системы с двумя и тремя степенями свободы.

Развитие систем автоматизации производства, создание роботизированных производств, с одновременно функционирующими несколькими роботами, появление двуруких роботов требует развития методов построения и управления систем относительного манипулирования с числом степеней свободы от трех до двенадцати.

Вопросы классификации механизмов устройств относительного манипулирования впервые рассмотрены в работе [1]. В работах [1, 2] отмечены особенности устройств относительного манипулирования и решены вопросы анализа и синтеза устройств относительного манипулирования на основе механизмов с параллельной структурой. В работах [3–8] рассмотрены особенности построения алгоритмов управления двуруких роботов.

В настоящей статье рассмотрим задачи реализации заданных относительных движений рабочих звеньев двуруких роботов, в которых в качестве механических рук используются манипуляторы с тремя степенями свободы.

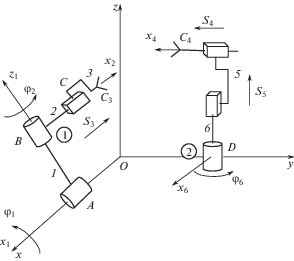
1. Манипуляционная система ВВП-ВПП. Рассмотрим манипуляционную систему ВВП-ВПП, содержащую два совместно работающих манипулятора: один с двумя вращательными и одной поступательной парами; второй с одной вращательной и двумя поступательными парами (рис. 1). Здесь и далее буквой “В” будем обозначать вращательные пары, буквой “П” поступательные.

Задача состоит в осуществлении заданного относительного движения выходного звена 4 манипулятора 2 относительно звена 3 манипулятора 1 по заданному закону. Этот закон движения будет задаваться матрицей четвертого порядка перехода от системы C₃x₃y₃z₃, связанной со звеном 3 к системе C₄x₄y₄z₄, связанный со звеном 4.

где α_ij (i, j = 1, 2, 3) являются функциями времени; a, b, c – координаты точки C₃ в системе C₄x₄y₄z₄.

Определению подлежат обобщенные координаты системы ${{\varphi }_{1}}$, ${{\varphi }_{2}}$, ${{s}_{3}}$, ${{s}_{4}}$, ${{s}_{5}}$, ${{\varphi }_{6}}$ – относительные перемещения соседних звеньев манипуляторов. Со звеньями манипуляторов свяжем системы координат, как показано на рис. 1. Со звеном манипулятора 1 свяжем систему координат Аx₁y₁z₁, направив Аx₁ по оси вращательной пары А, со звеном 2 свяжем систему координат Bx₂y₂z₂, направив ось Bz₂ по оси пары B, а ось Bx₂ по направлению линейного перемещению звена 3, со звеном 3 свяжем систему координат Cx₃y₃z₃ направив ось Cx₃ параллельно оси Bx₂, а ось Cz₃ параллельно оси Bz₂. Со звеньями манипулятора 2 свяжем системы координат следующим образом: со звеном 6 свяжем систему координат Dx₆y₆z₆, направив ось Dz₆ по оси пары D и оси Dx₆ параллельно направлению линейного перемещения в поступательной паре звена. Со звеньями 5 и 4 свяжем системы координат, оси которых параллельны осям системы Dx₆y₆z₆.

Запишем матрицы ориентации и положения системы координат C₃x₃y₃z₃ в системе Оxyz в виде двух матриц третьего порядка, используя переход через звенья манипулятора 2. Матрица ориентации имеет вид

Координаты точки C₃ в системе Oxyz равны

здесь b₁ = b₀ + b, b₀ = OD.

Запишем матрицы, используя переход через звенья манипулятора 1, получим

Перемножив матрицы в (4) получим

Координаты точки C₃ в системе Oxyz также равны

где l₁ = AB.

Приравнивая элементы матриц (2) (5) и (3) (6) получим уравнения для определения выражений обобщенных координат, которые в данном случае являются управляющими функциями. Из этих уравнений получим

Перемещения ${{s}_{3}}$, ${{s}_{4}}$, ${{s}_{5}}$ в кинематических парах находятся из линейных уравнений $x_{{{{C}_{3}}}}^{{\left( 1 \right)}} = x_{{{{C}_{3}}}}^{{\left( 2 \right)}}$.

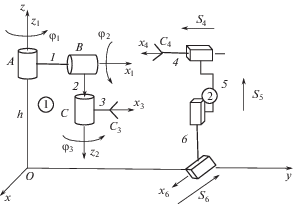
2. Манипуляционная система ВВВ-ППП. Рассмотрим манипуляционную систему типа ВВВ-ППП, состоящую из двух модулей-манипуляторов с открытой кинематической цепью.

Первый манипулятор содержит три вращательные пары – В. Второй манипулятор содержит три поступательные кинематические пары – П, реализующие движение вдоль осей системы Oxyz (рис. 2).

Со звеньями манипулятора 1 свяжем декартовы системы координат следующим образом: ось Az₁ системы координат Ax₁y₁z₁ первого звена направим по оси пары A, а ось Ax₁ по оси пары B, ось Bz₂ системы координат Bx₂y₂z₂ звена 2 направим по оси пары C, а ось Bx₂ по оси пары B, ось Сz₃ системы координат Cx₃y₃z₃ звена 3 направим по оси пары C, а ось Cx₃ по оси звена 3.

Задача состоит в реализации заданного закона движения звена 4 манипулятора 2 как твердого тела относительного звена 3 манипулятора 1. Относительное движение выходящих звеньев 3 и 4 будем определять матрицей четвертого порядка, как и для предыдущего механизма в виде (1).

Определению подлежат обобщенные координаты системы ${{{\varphi }}_{1}}$, ${{{\varphi }}_{2}}$, ${{{\varphi }}_{3}}$, ${{s}_{4}}$, ${{s}_{5}}$, ${{s}_{6}}$ – относительные перемещения соседних звеньев.

Матрица ориентации L₀₃ системы Cx₃y₃z₃ относительно системы Oxyz равна $L_{{03}}^{{\left( 1 \right)}} = {{L}_{{01}}}{{L}_{{12}}}{{L}_{{23}}}$, где ${{L}_{{01}}} = \left[ {\begin{array}{*{20}{c}} {\cos {{\varphi }_{1}}}&{ - \sin {{\varphi }_{1}}}&0 \\ {\sin {{\varphi }_{1}}}&{\cos {{\varphi }_{1}}}&0 \\ 0&0&1 \end{array}} \right]$;

Для координат точки C₃ в неподвижной системе координат получим

Здесь ${{\varphi }_{1}}$, ${{\varphi }_{2}}$, ${{\varphi }_{3}}$ углы относительного поворота звеньев 1, 2, 3; l₃ = СС₃; l₂ = BС; h = AO; l₁ = AB.

Угловую ориентацию системы C₃x₃y₃z₃ относительно системы Oxyz найдем, перемножая матрицы относительного поворота.

Матрица (8) и матрица (9) вместе образуют матрицу L₀₃ четвертого порядка, определяющую положение и ориентацию звена 3 в неподвижной системе координат Oxyz. Матрица ориентации системы C₃x₃y₃z₃ в системе Oxyz через звенья 2 в данном случае является единичной. Координаты точки C₃ в системе Oxyz через параметры манипулятора 2.

Приравнивая соответствующие элементы матриц (8) и (10) получим уравнение для определения обобщенных координат системы, управляющих функций, реализующих заданное относительное перемещение выходных звеньев манипуляторов

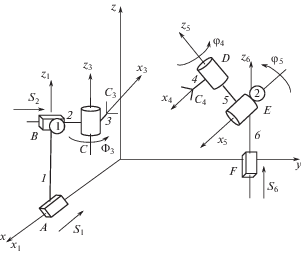
3. Манипуляционная система ППВ-ПВВ. Рассмотрим манипуляционную систему, содержащую два манипулятора типа ППВ-ПВВ, где П – поступательная пара, В – вращательная пара (рис. 3).

Манипулятор 1 содержит две поступательные и одну вращательную кинематическую пары. При этом линейные перемещения звена осуществляются параллельно оси Ох, перемещение звена 2 перпендикулярно перемещению звена 1. Ось вращения звена 3 перпендикулярна перемещению звена 2. Манипулятор 2 содержит одну поступательную и две вращательные кинематические пары, при этом, звено 6 совершает поступательные движения вдоль оси Oz, ось вращения звена 5 перпендикулярна направлению движения звена 6, ось вращения звена 4 перпендикулярна оси вращения звена 5.

Обобщенными координатами механизма являются величины относительных перемещений звеньев манипуляторов ${{s}_{1}}$, ${{s}_{2}}$, ${{\varphi }_{3}}$, ${{s}_{4}}$, ${{\varphi }_{5}}$, ${{\varphi }_{6}}$.

Выводными звеньями манипуляторов являются звенья 3 и 4.

Относительное положение звена 4 относительно звена 3 определяем матрицей M₃₄ перехода от системы C₄x₄y₄z₄, связанной со звеном 4 к системе C₃x₃y₃z₃, связанной со звеном 3

Левые три столбца и три строки представляют матрицу ориентации, где ${{\alpha }_{{ij}}}$ $(i,j = 1,~2,~3)$ направляющие косинусы осей C₄x₄y₄z₄; r = [a, b, c]^T – координаты точки C₄ в системе C₃x₃y₃z₃. Задача реализации заданного относительного движения выходных звеньев манипуляторов состоит в определении обобщенных координат по заданной матрице (11).

Для решения задачи со звеньями манипуляторов свяжем системы координат следующим образом: для манипулятора 1 со звеном 1 свяжем систему координат А₁x₁y₁z₁, направив ось Аx₁ по оси Ох, а ось Аz₁ – параллельно Oz; со звеном 2 свяжем систему координат Сx₂y₂z₂, направив ось Cz₂ по оси пары С, параллельно оси z, а ось Сy₂ – параллельно Оу.

Для манипулятора 2 со звеньями свяжем системы координат следующим образом: со звеном 6 свяжем систему координат Еx₆y₆z₆ направив ось Еz₆ параллельно оси Oz, а ось x₆ по вращательной паре Е; со звеном 5 свяжем систему координат Еx₅y₅z₅, направив ось Еx₅ по оси пары Е, а ось z₅ по оси пары D. Со звеном 4 свяжем систему координат Dx₄y₄z₄ направив ось Dz₄ по оси пары D, а ось x₄ – по оси звена 4.

Запишем матрицу ориентации системы Cx₄y₄z₄, связанной со звеном 4 в неподвижной системе координат через звенья манипулятора 1, получим

Координаты точки C₄ в системе Oxyz через параметры манипулятора 1 равны

где l₁ и l₃ – длина звена 1 и 3.

Далее запишем матрицу M₀₄ через звенья манипулятора 2. Матрица ориентации звена 4, равна

где L_{i, i – 1} матрицы перехода от системы (i – 1) к системе i.

Подставляя их выражения в (14) и перемножая матрицы получим матрицу третьего порядка ориентации звена 4 в системе Oxyz

Координаты точки C₄ в системе Oxyz через параметры манипулятора 2 равны

Здесь l₄ и l₅ – длины звеньев 4 и 5; s₆ – перемещение звеньев 6 в паре F.

Приравнивая соответствующие элементы матриц (12), (15) и (13), (16) получим уравнения для определения выражений обобщенных координат, которые в данном случае являются управляющими функциями. Из этих уравнений получим

Уравнения обобщенных координат манипуляторов согласно (17) реализуют заданное относительное движение их выходных звеньев согласно матрице (11).

Заключение. Получены соотношения для управляющих переменных, позволяющие реализовать заданное относительное движение двух твердых тел с шестью степенями свободы с помощью двух манипуляторов с тремя степенями свободы каждый. Оба манипулятора совместно должны иметь не менее трех вращательные кинематических пар. Полученные соотношения можно использовать для построения алгоритмов управления двуруких роботов с шестью степенями свободы.