1. На главную
  2. Электронные версии
  3. Проблемы машиностроения и надежности машин
  4. № 5, 2020

Проблемы машиностроения и надежности машин, 2020, № 5, стр. 3-10

Оценка тепловой и акустической энергий при схлопывании кавитационного пузырька

А. А. Аганин 1, О. Р. Ганиев 1, А. И. Давлетшин 1, *, Л. Е. Украинский 1

1 Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия

* E-mail: anas.davletshin@gmail.com

Поступила в редакцию 31.10.2019
Принята к публикации 29.05.2020

Полный текст (PDF)

Аннотация

Приводятся результаты численного исследования тепловой и акустической энергий, выделяемых при схлопывании одиночного сферического кавитационного пузырька в воде при давлении 10 бар и температуре 20°С. В используемой модели принимаются во внимание теплопроводность пара в пузырьке и окружающей жидкости, теплообмен, испарение/конденсация на поверхности пузырька, сжимаемость жидкости. Преобразование механической энергии в тепловую за счет вязкости жидкости не учитывается. Показано, что при схлопывании пузырька энергия акустического излучения, обусловленного радиальными пульсациями пузырька, примерно в 9 раз больше энергии, затрачиваемой на нагрев жидкости. Величина этих энергий изменяется пропорционально кубу начального радиуса пузырька.

Ключевые слова: кавитационный пузырек, паровой пузырек, коллапс пузырька, захлопывание пузырька, радиальные пульсации пузырька, поступательное движение пузырька, нагрев жидкости, акустическое излучение

Известно, что кавитация жидкости обладает многочисленными эффектами. В частности, при сферическом (или близком к нему) коллапсе пузырька в его полости могут возникать радиально сходящиеся ударные волны [1], в пузырьке могут сильно повышаться давление, температура и плотность [2], может возникать свечение [3]. В конце коллапса, близкого к сферическому, в окружающем пузырек слое жидкости может сильно возрастать давление [4], в жидкость могут излучаться радиально расходящиеся акустические и ударные волны [5]. При несферическом коллапсе на поверхности пузырька могут образовываться высокоскоростные кумулятивные струйки [6] и т. д.

На практике эффекты кавитации зачастую вызывают проблемы. Так, известно, что кавитация может приводить к повреждению поверхностей тел [7, 8], шуму [9], понижению эффективности работы устройств [10] и др. Вместе с тем, эффекты кавитации также и широко применяются. Кавитация используется, например, для очистки труб теплообменных аппаратов от отложений [11], повышения эффективности волновых технологий [12], нагрева жидкости с помощью вихревых теплогенераторов [13, 14].

В настоящей статье рассматриваются эффекты нагрева жидкости и акустического излучения при захлопывании одиночного кавитационного пузырька в неограниченном объеме неподвижной жидкости.

Постановка задачи. Изучается величина тепловой и акустической энергий, выделяемых при захлопывании в жидкости (воде) одиночного сферического кавитационного (парового) пузырька. Изначально (в момент времени t = 0) пар в пузырьке и окружающая жидкость покоятся, температура пара и жидкости Т0 = 20°С, пар находится в состоянии насыщения при давлении pS(T0) = 0.022 бар. Давление жидкости вдали от пузырька p∞ = 10 бар. Схлопывание пузырька обусловлено тем, что давление жидкости p∞ намного превышает начальное давление в пузырьке pS(T0).

В настоящей статье при моделировании захлопывания пузырька считается, что пар в его полости и окружающая жидкость являются теплопроводными, а на поверхности пузырька реализуется тепломассообмен. Пар в пузырьке полагается совершенным газом с давлением, зависящим только от времени. Жидкость принимается слабосжимаемой, что позволяет учесть эффект акустического излучения. Влияние вязкости жидкости на преобразование энергии радиальных пульсаций пузырька в тепловую не учитывается.

Математическая модель. Математическая формулировка задачи представляет собой систему дифференциальных уравнений [15]

(1)
$\begin{gathered} \left( {1 - \frac{{{{u}^{ + }}}}{{{{c}_{L}}}}} \right)R{{{\dot {u}}}^{ + }} + \frac{3}{2}\left( {1 - \frac{{{{u}^{ + }}}}{{3{{c}_{L}}}}} \right){{u}^{ + }}^{2} + 2\left( {1 - \frac{{{{u}^{ + }}}}{{4{{c}_{L}}}}} \right){{u}^{ + }}\left( {\dot {R} - {{u}^{ + }}} \right) = \\ \, = \left( {1 + \frac{{\dot {R}}}{{{{c}_{L}}}}} \right)\frac{{{{p}^{ + }} - {{p}_{\infty }}}}{{{{\rho }_{L}}}} + \frac{R}{{{{c}_{L}}}}\frac{{{{{\dot {p}}}^{ + }} - {{{\dot {p}}}_{\infty }}}}{{{{\rho }_{L}}}}, \\ \end{gathered} $
(2)
${{\dot {p}}^{ - }} = \frac{3}{R}[(\gamma - 1){{({{\kappa }_{v}}{{T}_{r}})}^{ - }} - \gamma p{{u}^{ - }}],$
$\dot {R} = {{u}^{ + }} + \frac{j}{{{{\rho }_{L}}}},$
${{T}_{t}} + u{{T}_{r}} = \frac{{(\gamma - 1)T}}{{\gamma p}}\left( {{{{\dot {p}}}^{ - }} + \frac{1}{{{{r}^{2}}}}{{{({{r}^{2}}{{\kappa }_{v}}{{T}_{r}})}}_{r}}} \right),$
${{\rho }_{L}}C{{r}^{2}}\left( {{{T}_{t}} + \frac{{{{R}^{2}}}}{{{{r}^{2}}}}{{u}^{ + }}{{T}_{r}}} \right) = {{({{\kappa }_{L}}{{r}^{2}}{{T}_{r}})}_{r}},$

Здесь точка сверху означает производную по времени t, r – расстояние до центра пузырька, R – радиус пузырька, u – скорость, p – давление, T – температура, ρ – плотность, с – скорость звука, κ – коэффициент теплопроводности, нижние индексы L и ${v}$ указывают на отношение к жидкости и пару соответственно, верхние знаки + и – указывают на отношение к поверхности пузырька со стороны жидкости и пара соответственно, γ – показатель адиабаты пара, С – удельная теплоемкость жидкости. Кроме того, имеем

${{p}^{ + }} = {{p}^{ - }} - \frac{{2\sigma }}{R} - \frac{{4\mu }}{R}{{u}^{ + }},\quad u = \frac{r}{R}{{u}^{ - }} + \frac{{\gamma - 1}}{{\gamma p}}\left( {{{\kappa }_{v}}{{T}_{r}} - \frac{r}{R}{{{({{\kappa }_{v}}{{T}_{r}})}}^{ - }}} \right),$
${{u}^{ - }} = \frac{j}{{{{\rho }^{ - }}}} - \dot {R},\quad {{\rho }^{ - }} = \frac{{{{p}^{ - }}}}{{{{R}_{v}}T{\kern 1pt} *}},\quad j = \frac{{{{\alpha }_{M}}}}{{\sqrt {2\pi {{R}_{v}}} }}\left( {\frac{{{{p}_{S}}(T{\kern 1pt} *)}}{{\sqrt {T{\kern 1pt} *} }} - \frac{{\Gamma {{p}^{ - }}}}{{\sqrt {T{\kern 1pt} *} }}} \right),$
$\Gamma = {{{\text{e}}}^{{ - {{\Omega }^{2}}}}} - \Omega \sqrt \pi \left( {1 - \frac{2}{{\sqrt \pi }}\mathop {\mathop \smallint \limits_0 }\limits^\Omega {{{\text{e}}}^{{ - {{x}^{2}}}}}{\text{d}}x} \right),\quad \Omega = \frac{j}{{{{p}^{ - }}}}\sqrt {\frac{{{{R}_{v}}T{\kern 1pt} *}}{2}} ,$
где σ – коэффициент поверхностного натяжения, μ – коэффициент вязкости жидкости, ${{R}_{v}}$ – газовая постоянная для пара, αM – коэффициент аккомодации (испарения/конденсации), Т* – температура на поверхности пузырька, ${{p}_{S}}$(T) – давление насыщенных паров при температуре T.

Граничные условия для уравнений теплопроводности пара (4) и жидкости (5) являются

$r = 0{\kern 1pt} :\;\;{{T}_{r}} = 0,$
$r = \infty {\kern 1pt} :\;\;T = {{T}_{0}},\quad p = {{p}_{\infty }}$
$r = R{\kern 1pt} :\;\;{{({{\kappa }_{L}}{{T}_{r}})}^{ + }} - {{({{\kappa }_{v}}{{T}_{r}})}^{ - }} = jl({{p}^{ - }}),\quad {{T}^{ + }} = {{T}^{ - }} = T{\kern 1pt} *$

Здесь l(p–) – скрытая теплота парообразования при давлении р–.

Начальные условия (при $t = 0$) для уравнений (1)–(5) имеют вид

${{u}^{ + }} = 0,\quad {{p}^{ - }} = {{p}_{S}}({{T}_{0}}),\quad R = {{R}_{0}};\quad T = {{T}_{0}}\quad {\text{при}}\quad 0{\text{ }} \leqslant r < \infty .$

В рамках принятых условий имеем: ρL = 998.2 кг/м3, сL = 1483 м/с, κL = 0.5984 Вт/(м К), ${{\kappa }_{v}}$ = 0.018222 Вт/(м К), γ = 1.325, С = 4150 Дж/(кг K), σ = 0.0725 Н/м, μ = 103 кг/(м с), ${{R}_{v}}$ = 461.912 Дж/(кг K), αM = 0.04.

Основные положения методики численного решения. В методике численного решения задачи (1)–(9) применяется замена переменных r = Rη, t = τ. В результате для произвольной функции  f имеем

${{f}_{t}} = {{f}_{\tau }} - \eta \frac{{\dot {R}}}{R}{{f}_{\eta }},\quad {{f}_{r}} = \frac{1}{R}{{f}_{\eta }},\quad \left. {{{f}_{r}}} \right|_{{r = R}}^{ - } = {{\left. {\frac{1}{R}{{f}_{\eta }}} \right|}_{{\eta = 1}}}.$

В терминах координаты η области пузырька соответствует интервал 0 ≤ η < 1, а области жидкости – интервал 1 < η ≤ ηL, где ηL определяет положение внешней границы расчетной области жидкости. В ходе радиальных пульсаций пузырька в окрестности его поверхности с обеих ее сторон могут возникать очень тонкие тепловые погранслои. С учетом этого применяются сетки, сгущающиеся к поверхности пузырька по геометрической прогрессии.

Алгоритм расчета задачи (1)–(9) в указанных новых переменных основан на методе конечных разностей. При этом пространственные производные аппроксимируются центральными разностями всюду, за исключением поверхности пузырька. На поверхности пузырька используются односторонние аппроксимации второго порядка точности. Замена пространственных производных конечными разностями сводит дифференциальные уравнения в частных производных (4), (5) к системе обыкновенных дифференциальных уравнений относительно температуры T в узлах разностной сетки. Эта система оказывается связанной с обыкновенными дифференциальными уравнениями (1)–(3) относительно u+, $\dot {R}$ и p– лишь посредством параметров j(T*), $\kappa {{T}_{r}}{{{\text{|}}}^{ - }}$ и l(p–). Уравнения (1)–(3) решаются методом Дормана–Принса [16], являющимся высокоточным вариантом метода Рунге–Кутты с автоматическим выбором шага интегрирования по времени. Указанная система относительно температуры T в узлах разностной сетки рассчитывается частично неявным методом с использованием пятиточечной прогонки.

Расчет ведется с применением единого временного шага. При этом на очередном временном шаге при расчете новых значений u+, $\dot {R}$, p– считаются неизменными температура T– и ее градиент $T_{r}^{ - }$ на поверхности пузырька, а при расчете нового поля температуры T в пузырьке и жидкости в качестве неизменных принимается давление p–. При таком подходе проблем с устойчивостью расчетов не возникает. Вместе с тем, его точность определяется точностью решения уравнений (4), (5), которая автоматически не контролируется. Поэтому требуемая точность расчетов достигается путем последовательного сгущения пространственной сетки, используемой для решения уравнений (4), (5).

Результаты. Представленные в разделах 1–3 результаты получены для начального радиуса пузырька R0 = 0.5 мм.

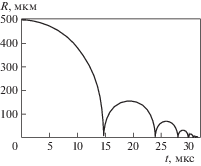
1. Особенности схлопывания пузырька. Рис. 1 иллюстрирует изменение радиуса пузырька при его схлопывании.

Рис. 1.

Уменьшение радиуса пузырька при схлопывании.

Видно, что схлопывание реализуется в виде ряда быстро затухающих радиальных пульсаций, в конце которых пузырек исчезает. Довольно быстрое схлопывание пузырька обусловлено, главным образом, сжимаемостью жидкости и конденсацией пара на межфазной поверхности.

На рис. 2 показано изменение температуры пара в центральной области пузырька, где влияние теплообмена с жидкостью незначительно, и давление пара, которое в рамках принятой модели зависит только от времени (одинаково по всему объему пузырька).

Рис. 2.

Изменение температуры в центре пузырька (а) и давления в его полости (б) в процессе схлопывания.

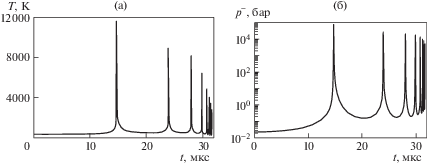
Видно, что как температура пара, так и его давление в моменты локальных экстремальных сжатий пузырька постепенно уменьшаются. В моменты же максимального расширения пузырька температура после первых двух сжатий несколько возрастает, а затем падает, тогда, как давление все время монотонно увеличивается.

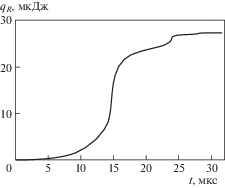
2. Оценка приходящей в жидкость тепловой энергии. Приходящую из пузырька энергию qR, затрачиваемую на нагрев жидкости, можно рассчитать по формуле

${{\dot {q}}_{R}} = - 4\pi {{\kappa }_{L}}\left. {{{T}_{r}}} \right|_{{r = R}}^{ + }{{R}^{2}},$
где $\left. {{{T}_{r}}} \right|_{{r = R}}^{ + }$ – градиент температуры жидкости на поверхности пузырька.

Рис. 3 демонстрирует изменение qR согласно (10) в процессе схлопывания пузырька. Видно, что величина qR в процессе схлопывания монотонно возрастает. При этом наибольший ее прирост наблюдается в ходе первого сжатия и последующего расширения пузырька. После второго расширения величина qR увеличивается незначительно. Это, по-видимому, объясняется довольно быстрым уменьшением площади поверхности пузырька, через которую реализуется теплообмен между пузырьком и жидкостью. Согласно рис. 3, энергия E, поступившая на нагрев жидкости, примерно равна 27 мкДж.

Рис. 3.

Изменение тепловой энергии, уходящей в жидкость из пузырька в процессе его схлопывания.

3. Оценка энергии акустического излучения. Для оценки энергии акустического излучения были проведены расчеты рассматриваемой задачи без учета влияния сжимаемости жидкости, определяющей акустическое излучение. С этой целью в уравнении (1) полагалось cL = ∞. Результаты расчетов представлены на рис. 4. Без учета акустического излучения основным механизмом, определяющим скорость захлопывания пузырька, является эффект испарения/конденсации. На рис. 4а видно, что в этом случае процесс захлопывания пузырька сильно (более чем в 1000 раз) замедляется. Момент исчезновения пузырька при учете акустического излучения в расчетах без его учета приближенно соответствует моменту достижения радиусом пузырька своего максимального значения в ходе первого локального расширения пузырька, следующего за его первым локальным сжатием. Указанное максимальное значение радиуса очень мало отличается от его начального значения, что, наряду с рис. 4а также свидетельствует о медленном затухании радиальных пульсаций пузырька.

Рис. 4.

Изменение радиуса пузырька R ((а), (б)) и уходящей из пузырька тепловой энергии qR жидкости ((в), (г)) в ходе всего процесса схлопывания пузырька ((а), (в)) и в его начальном промежутке ((б), (г)) без учета сжимаемости жидкости (cL = ∞). Пунктирные линии на ((б), (г)) соответствуют сжимаемой жидкости (рис. 1, 3).

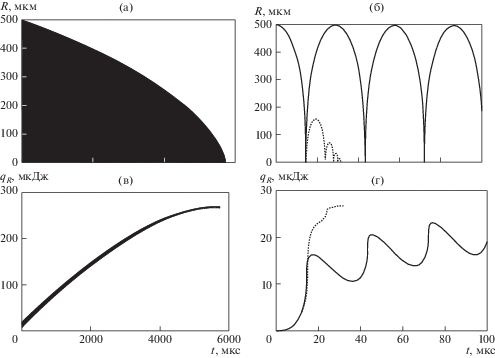
Из рис. 4в, г следует, что без учета акустического излучения величина уходящей из пузырька тепловой энергии Enoac (максимум величины qR, рассчитанной при cL = ∞) оказывается примерно в десять раз больше, чем при его учете. Отсюда следует, что энергия акустического излучения Eac = E noac – E ≈ 9E. На рис. 4г видно, что при пренебрежении акустическим излучением меняется также и характер теплообмена жидкости с пузырьком. Если при учете акустического излучения величина тепловой энергии увеличивается монотонно, то без его учета она растет в виде колебаний (с уменьшающейся амплитудой). Это означает, что при учете акустического излучения поток тепловой энергии в ходе всего процесса схлопывания пузырька направлен от пузырька к жидкости. Без учета излучения он направлен к жидкости лишь в большей части каждого локального сжатия пузырька, тогда как в большей части каждого локального расширения тепловая энергия уходит обратно из жидкости в пузырек.

4. Влияния размеров пузырька. Для оценки влияния размеров пузырька на величину энергии, ушедшей из пузырька на нагрев жидкости к концу его схлопывания и на энергию акустического излучения, были проведены расчеты для ряда значений начального радиуса пузырька R0 (рис. 5).

Рис. 5.

Влияние начального радиуса пузырька R0 на энергию E, ушедшую из пузырька на нагрев жидкости к концу его схлопывания с учетом (точки, соединенные пунктирной кривой) и без учета (точки, соединенные сплошной кривой) акустического излучения.

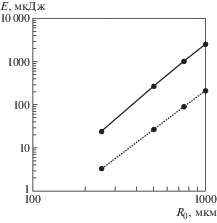
Видно, что в логарифмических шкалах обе зависимости от радиуса пузырька являются близкими к линейным. Анализ показывает, что обе зависимости близки к кубическим.

Отметим также, что в используемой модели (1)–(9) учитывается диссипация энергии радиальных пульсаций пузырька за счет вязкости жидкости. В реальности эта энергия трансформируется в тепловую энергию жидкости. В модели настоящей работы эта трансформация не учитывается. Для оценки потерь тепловой энергии жидкости, не учтенных при указанной трансформации, были проведены расчеты рассматриваемой задачи без учета влияния вязкости жидкости, т.е. при μL = 0. Расчеты показали, что потери тепловой энергии жидкости за счет отсутствия в используемой модели (1)–(9) трансформации энергии вязкой диссипации радиальных пульсаций пузырька незначительны.

Заключение. Представлены результаты численного исследования тепловой и акустической энергий, выделяемых при захлопывании в жидкости (воде) одиночного сферического кавитационного (парового) пузырька. Давление жидкости 10 бар, ее температура 20°С. Применяется физическая модель, в которой пар в пузырьке и окружающая жидкость считаются теплопроводными, а на поверхности пузырька реализуется тепломассообмен. Учитывается акустическое излучение, обусловленное сжимаемостью жидкости. Влияние вязкости вне поверхности пузырька на преобразование механической энергии в тепловую не учитывается. Пар в пузырьке считается совершенным газом с давлением, зависящим только от времени.

Показано, что при схлопывании пузырька с начальным радиусом 0.5 мм в жидкость поступает энергии около 25 мкДж, которая затрачивается на нагрев жидкости. При этом посредством акустического излучения, являющегося результатом радиальных пульсаций пузырька, уносится энергии примерно в девять раз больше, тогда как энергия, обусловленная диссипацией радиальных пульсаций пузырька за счет вязкости жидкости (в модели настоящей работы трансформация этой энергии в тепловую не учитывается) является незначительной. Установлено, что энергия, затрачиваемая на нагрев жидкости, и энергия, уносимая акустическим излучением, пропорциональны кубу начального радиуса пузырька.

Следует отметить, что в используемой модели не учитывается влияние ряда важных факторов, в частности, деформирования пузырька, зависимости коэффициентов теплопроводности от температуры, несовершенства пара и т.д. Их учет представляет собой весьма нетривиальную задачу. В этом смысле представленные результаты можно рассматривать как первое приближение, которое дает хороший ориентир для проведения последующих исследований с применением более адекватных моделей.

Список литературы

  1. Wu C.C., Roberts P.H. A model of sonoluminescence // Proc. R. Soc. Lond. A. 1994. V. 445. P. 323.

  2. Moss W.C., Clarke D.B., Young D.A. Calculated Pulse Widths and Spectra of a Single Sonoluminescencing bubble // Science. 1997. V. 276. P. 1398.

  3. Gaitan D.F., Crum L.A., Roy R.A., Church C.C. Sonoluminescence and bubble dynamics for a single, stable cavitation bubble // JASA. 1992. V. 91. P. 3166.

  4. Rayleigh Lord. On the pressure developed in a liquid during the collapse of a spherical cavity // Philosophical Magazine. 1917. V. 34. № 200. P. 94.

  5. Akhatov I., Linday O., Topolnikov A., Mettin R., Vakhitova N., Lauterborn W. Collapse and rebound of a laser-induced cavitation bubble // Physics of Fluids. 2001. V. 13. № 10. P. 2805.

  6. Воинов О.В., Воинов В.В. О схеме захлопывания кавитационного пузырька около стенки и образования кумулятивной струи // ДАН СССР. 1976. Т. 227. № 1. С. 63.

  7. Pearsall I.S. Cavitation. Mills and Boon Limited London. 1972.

  8. Brennen C.E. Hydrodynamics of pumps. Oxford university press. 1994.

  9. Harrison M. An experimental study of single bubble cavitation noise // JASA. 1982. V. 24. № 6. P. 776.

  10. Philipp A., Lauterborn W. Cavitation erosion by single laser-produced bubbles // J. Fluid Mech. 1998. V. 361. P. 75.

  11. Kieser B., Phillion R., Smith S., McCartney T. The application of industrial scale ultrasonic cleaning to heat exchangers // Proceed of Int. Conf. on Heat exchanger fouling and cleaning. 2011. P. 336.

  12. Ганиев Р.Ф., Украинский Л.Е. Нелинейная волновая механика и технологии. Волновые и колебательные явления в основе высоких технологий. Изд. 2-е, М.: Институт компьютерных исследований; Научно-издательский центр “Регулярная и хаотическая динамика”, 2011. 780 с.

  13. Бритвин. Л.Н. Теплогенератор кавитационно-вихревого типа. РФ Патент 99110397/06, 2001.

  14. Бирюк В.В., Серебряков Р.А., Достовалова С.С. Вихревой гидравлический теплогенератор с улучшенными характеристиками // Известия Самарской государственной сельскохозяйственной академии. 2015. № 3. С. 70.

  15. Nigmatulin R.I., Akhatov I.Sh., Topolnikov A.S., Bolotnova R.Kh., Vakhitova N.K., Lahey R.T. (Jr), Taleyarkhan R.P. The Theory of Supercompression of Vapor Bubbles and Nano-Scale Thermonuclear Fusion // Physics of Fluid. 2005. V. 17. P. 107.

  16. Хайрер Э., Нерсетт С., Виннер Г. Решение обыкновенных дифференциальных уравнений. Нежесткие задачи. М.: Мир, 1990. 512 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал