Проблемы машиностроения и надежности машин, 2020, № 5, стр. 11-20

Рассматривается задача о вынужденных колебаниях оболочечной конструкции со свободными граничными условиями на торцах. Конструкция состоит из секций, каждая из которых представляет собой конечную упругую цилиндрическую оболочку с упругими кольцами на концах. На оболочечную конструкцию действуют дискретные вынуждающие силы. В теории колебаний конечных цилиндрических оболочек одной из ранних и наиболее известных является работа Форсберга [1], но в ней рассматриваются только собственные колебания “сухой” цилиндрической оболочки (в вакууме). Вынужденные колебания бесконечной цилиндрической оболочки в жидкости, возбуждаемые сосредоточенной силой в виде δ-функции Дирака рассмотрены в [2]. Попытки решения задачи вынужденных колебаний конечных цилиндрических оболочек в жидкости методом конечных элементов нельзя признать удобными и успешными [3].

Причин, по которым требуется рассмотрение данной задачи, две: 1) знание распределения виброперемещений на поверхности оболочки необходимо для решения задачи излучения; 2) численно-аналитические методы расчета вынужденных колебаний конечных составных оболочечных конструкций практически отсутствуют.

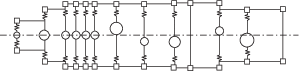
В общем случае оболочечная конструкция состоит из цилиндрических оболочек и колец, на которых установлено амортизированное оборудование. Оболочки подкреплены стрингерами и шпангоутами. Шпангоуты также моделируются упругими кольцами. Амортизированное оборудование представляется в виде сосредоточенных масс, закрепленных на кольцах. Пример динамической модели оболочечной конструкции приведен на рис. 1.

Решается задача – разработать численно-аналитический метод расчета вынужденных колебаний системы, представляющей собой оболочечную конструкцию, включающую набор подкрепленных цилиндрических оболочек и колец, возбуждаемых дискретными вынуждающими силами. Полученные результаты будут использованы в дальнейшем для разработки метода расчета вынужденных колебаний конечной оболочечной конструкции, погруженной в жидкость.

Для формирования матричного уравнения движения системы предложен метод (способ), идея которого состоит в следующем. Система (динамическая модель) условно разбивается на подсистемы, включающие оболочки и кольца. Для каждой оболочки составляются дисперсионные уравнения и определяются их корни. Решение свободных колебаний оболочки записывается в виде вектора (матрицы-столбца) перемещений, состоящего из четырех элементов (u, $v$, w, w'). Функция распределения перемещений оболочек по их длине записывается через перемещения торцевых сечений. Внутренние силы в оболочках тоже приводятся к торцам оболочки. Определяются матрицы динамических жесткостей колец по соответствующим четырем перемещениям. Общее матричное уравнение вынужденных колебаний всей оболочечной конструкции записывается как для простой цепной системы, состоящей из масс и пружин. Вынуждающие силы приложены к кольцам и распределены по окружному углу φ по гармоническому закону P = p cos nφ. Предложенный метод можно охарактеризовать как разновидность прямого метода. Его особенности заключаются в том, что, по аналогии с цепной системой, роль пружин выполняют упругие цилиндрические оболочки, а роль масс – упругие кольца. Для решения вынужденных колебаний оболочек используются уравнения свободных колебаний оболочек. Упругие кольца могут быть как реальными, так и фиктивными. Преимущества метода заключаются в том, что он позволяет легко изменять конфигурацию динамической модели в процессе проведения расчетов. Он позволяет задавать дискретные вынуждающие силы в любом месте по длине цилиндрической оболочки без применения δ-функции. Дискретные силы можно задать в любом поперечном сечении оболочки с использованием “фиктивных” колец (в которых не учитываются их массы). В результате получается матричное уравнение ленточного типа, состоящее из диагонально расположенных блок-матриц четвертого порядка, что позволяет упростить составление и ускорить решение матричных уравнений высокого порядка (порядка нескольких сотен).

Общий подход к расчету колебаний систем с распределенными параметрами известен. В данном случае уравнения движения цилиндрической оболочки в перемещениях, основанные на моментной теории упругих оболочек Кирхгофа–Лява, имеют вид [1, 4, 5]

где u, $v$, w – осевые (продольные), окружные (касательные) и радиальные перемещения оболочки; T₁, T₂, S, H, M₁, M₂ – упругие силовые факторы; q₁, q₂, q₃ – поверхностные нагрузки; a – радиус оболочки; h – толщина оболочки; ξ = x/a и φ – координаты в осевом и окружном направлениях; t – время; ${{\rho }_{*}}$ – плотность материала оболочки; 0 ≤ x ≤ L, L – длина оболочки.

Запишем решение уравнений свободных колебаний конечной цилиндрической оболочки (1) в форме [5]

где n – окружные гармоники ряда Фурье, n = 0, 1, 2, 3, …, α_jn – корни дисперсионного уравнения;  j = 1–8 – порядковые номера корней; С_jn – искомые коэффициенты; $\Delta $_jn – миноры матрицы уравнения движения оболочки (3); ω = 2πf – угловая частота колебаний; f – частота колебаний. В решение (2) входят подлежащие определению корни дисперсионного уравнения α_jn и коэффициенты С_jn. Для получения дисперсионного уравнения примем q₁ = q₂ = q₃ = 0 и решение уравнения представим в упрощенном виде

В результате подстановки этих решений в уравнение (1) получим уравнение свободных колебаний оболочки в матричном виде [6]

Элементы L_ij матрицы уравнения (3) будут

где a₁, b₁ – параметры стрингеров; а₂, b₂, z₂ – параметры шпангоутов; E = E₀(1 + iη) – комплексный модуль упругости; η – потери в материале оболочки; r = a – радиус оболочки; μ – коэффициент Пуассона; i = $\sqrt { - 1} $.

Каждое из решений U, V, W (2) состоит из восьми слагаемых по числу концевых граничных условий оболочки. Соответственно числу слагаемых для каждой гармоники n и для каждой частоты колебаний ω надо определить восемь корней α_j, входящих в перемещения U, V, W (2).

Матричное уравнение (3) можно представить в виде

Дисперсионное уравнение определяется из условия

где определитель матрицы

Решение дисперсионного уравнения (5) сводится к решению биквадратного полинома

Параметры полинома А₈, А₆, А₄, А₂, А₀ не выписаны из-за их громоздкости, обусловленной выражениями (4). В результате решения биквадратного полинома (6) получаем четыре квадратных корня, после извлечения квадратов получаем восемь комплексных корней, из них четыре корня положительных и четыре корня отрицательных. Модули у соответствующих положительных и отрицательных корней одинаковые. Корни дисперсионного уравнения определяются для каждой отдельной оболочки, входящей в оболочечную конструкцию.

Для составления уравнений вынужденных колебаний оболочечной конструкции, состоящей из набора оболочек, соединенных между собой кольцами каждое уравнение движения записывается для перемещений трех соседних подсистем с номерами: k – текущей, (k – 1) – предыдущей и (k + 1)– последующей. Подсистемами являются оболочки и кольца. Внутренние силы оболочки, приложенные, например, к кольцу k, выражаются через перемещения концов оболочек, присоединенных к кольцу слева (в конце предыдущей оболочки (k – 1)) и справа (в начале последующей оболочки (k + 1)).

Определим перемещения торцевых сечений оболочек. Представим распределение перемещений по длине y для каждой оболочки с учетом дополнительной координаты w' = dw/dy в матричном виде

Дополнительная координата w′ введена для возможности формирования блок-матриц в уравнениях стыковки цилиндрических оболочек с кольцами по четырем основным силовым факторам. Выражение (7) используется для каждой оболочки при составлении системы уравнений движения для всей оболочечной конструкции в целом. Обозначим A(y) произведение матриц в правой части выражения (7)

Представим перемещения торцев оболочки, имеющей длину $\ell $, в начале при y = 0 и в конце y = $\ell $ в виде

Составим блок-матричное уравнение

Из этого уравнения определим вектор-столбец коэффициентов W  ⁰= {С₁ – С₈}

Текущие перемещения по длине оболочки, выраженные через перемещения ее торцов, определяются выражением

Таким образом, вектор перемещений оболочки с произвольным номером k

где $\zeta _{{k0}}^{{}} = \zeta _{k}^{{}}\left( 0 \right)$, $\zeta _{{k1}}^{{}} = \zeta _{{k1}}^{{}}\left( {{{\ell }_{k}}} \right)$ – перемещения торцевых сечений оболочки номера k, $С_{k}^{1} = {{\bar {С}}_{1}}$, $C_{k}^{2} = {{\bar {C}}_{2}}$.

Матрица G_k(y) размером 4 × 8 состоит из столбцов G_pk, в которых р = 1, 2, …, 8 по числу корней дисперсионного уравнения.

где $\Delta _{{pk}}^{1} = \Delta _{{}}^{1}\left( {{{\alpha }_{{pk}}}} \right)$, $\Delta _{{pk}}^{2} = \Delta _{{}}^{2}\left( {{{\alpha }_{{kp}}}} \right)$, $\Delta _{{pk}}^{3} = \Delta _{{}}^{3}\left( {{{\alpha }_{{pk}}}} \right)$ миноры матрицы уравнения (3).

Матрицы $C_{k}^{1}$, $C_{k}^{2}$ являются блоками размером 8 × 4 квадратной матрицы C_k размером 8 × 8

где $G_{{k0}}^{{}} = G_{k}^{{}}\left( 0 \right)$, $G_{{k1}}^{{}} = G_{k}^{{}}\left( {{{\ell }_{k}}} \right)$.

Приведем внутренние силы в оболочке к ее торцевым сечениям. Вектор-столбец внутренних сил в оболочке номера k имеет вид

Соответствие между этими внутренними силами и перемещениями оболочки (10) следующее: $u \to {{T}_{1}}$, ${v} \to {{T}_{{12}}}$, $w \to N$, $w_{k}^{'} \to M{\text{/}}r$.

Связь внутренних сил оболочки с перемещениями торцевых сечений оболочки можно представить вектором

где $G_{k}^{*}\left( y \right)$ – матрица размером 4 × 8, состоящая из столбцов $G_{{pk}}^{*}$

В случае, когда к кольцу (слева и справа) крепятся оболочки разного диаметра, необходимо выполнить соответствующее приведение координат (перемещений) торцов оболочек к центру масс поперечного сечения кольца. Векторы перемещений торцов оболочки $\zeta _{{k1}}^{{}} = H_{k}^{1}{{Z}_{k}}$, ${\text{ }}\zeta _{{k + 1,{\text{0}}}}^{{}} = H_{k}^{2}Z_{k}^{{}}$ можно выразить через векторы перемещений колец Z_k

с помощью матриц перехода $H_{k}^{1}$ и $H_{k}^{2}$

Внутренние силы, действующие в торцевых сечениях оболочек (в конце предыдущей оболочки η_k, l и в начале последующей оболочки η_k + 1.0), приведем к соединяющему их кольцу с помощью матриц приведения $H_{k}^{3}$ и $H_{k}^{4}$. Силы, приложенные к центру масс поперечного сечения кольца c номером k

где $\eta _{{k0}}^{{}} = \eta _{k}^{{}}\left( 0 \right)$; $\eta _{{k1}}^{{}} = \eta _{k}^{{}}\left( {{{\ell }_{k}}} \right)$;

Матричное уравнение движения оболочечной конструкции формируется следующим образом. С учетом принятых обозначений уравнение движения кольца номера k в матричной форме имеет вид

где P_k – вектор возмущающих сил; $F_{k}^{1}$, $F_{k}^{2}$ – векторы внутренних сил, приложенные от оболочек к кольцу слева и справа; М_k – матрица динамических жесткостей кольца номера k. Эту матрицу для n ≥ 1 можно представить в виде где EI – жесткость на изгиб; ρ – плотность материала кольца; F – площадь поперечного сечения кольца; R_k – радиус кольца.

Вектор перемещений кольца

Подставляя в уравнение движения кольца (12) значения сил (11) и перемещений оболочек (10), получим систему уравнений порядка 4(N + 1), где N – общее количество оболочек, (N + 1) – общее количество колец.

В уравнениях движения порядковые номера колец обозначим q, где 0 ≤ q ≤ p. Уравнения составляются для каждого кольца последовательно.

Для первого кольца q = 0

для каждого промежуточного кольца от q = 1 до q = N – 1 для последнего кольца q = N

Общее матричное уравнение для оболочечной конструкции имеет ленточную диагональную структуру расположения блок-матриц размером 4 × 4 и в сумме может иметь порядок нескольких сотен. В результате решения этой системы определяются искомые векторы перемещений колец Z_q оболочечной конструкции.

После определения векторов перемещений Z_q на кольцах q из уравнения (13) можно построить АЧХ колебаний в заданных сечениях (кольцах) оболочечной конструкции, а также формы вынужденных колебаний для каждой оболочки и всей оболочечной конструкции в целом.

Форма колебаний для каждой оболочки определяется выражением

Выражение (14) последовательно используется для каждой оболочки и затем методом припасовывания определяется форма колебаний всей оболочечной конструкции.

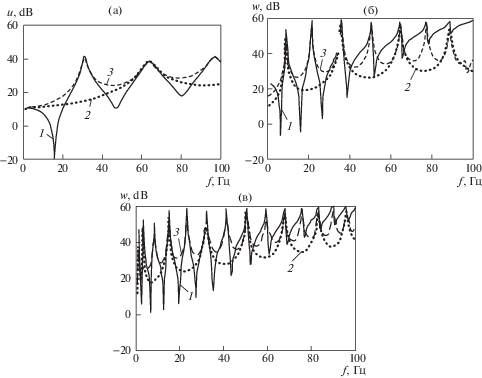
На основе изложенной методологии разработаны алгоритм и компьютерная программа на языке Fortran. С использованием программы проведены расчеты для оболочечной конструкции. В качестве примера на рис. 2a, б, в приведены АЧХ колебаний оболочечной конструкции, состоящей из восьми одинаковых секций с цилиндрическими оболочками постоянного радиуса в диапазоне частот f = 1–100 Гц для окружных гармоник n: (a) n = 0; (б) n = 1; (в) n = 2.

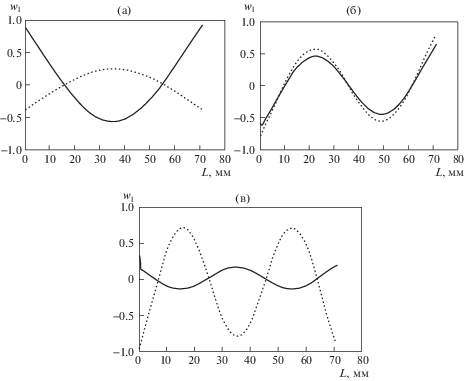
На рис. 2а показаны амплитуды ускорений продольных колебаний U в dB. На рис. 2б, в показаны амплитуды радиальных колебаний W в dB соответственно для гармоник n = 1 и n = 2. Геометрические параметры оболочечной конструкции L = 70.4 м, a = 4 м, h = 0.04 м. Возмущающая сила P = 1000 Н приложена на левом конце оболочечной конструкции. Линии на рис. 2а, б, в – сплошная, точками и штриховая соответствуют АЧХ в сечениях: 1 – левый конец; 2 – середина; 3 – правый конец оболочечной конструкции. На рис. 3а, б, в показаны формы радиальных колебаний W на частотах, близких к резонансам, показанным на АЧХ на рис. 2б: (а) f = 8.5 Гц; (б) f = 21 Гц; (в) f = 35 Гц. Сплошные линии – реальные составляющие Re(W), пунктирные линии – мнимые составляющие Im(W). Полученные формы колебаний соответствуют типичным балочным формам изгибных колебаний балки со свободными краями, что подтверждает правильность расчетов.