Проблемы машиностроения и надежности машин, 2020, № 5, стр. 95-107
Оценка концентрации напряжений вблизи захватов при растяжении образцов из полимерных композитов
А. Н. Полилов 1, *, Н. А. Татусь 1
1 Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия
* E-mail: polilovan@mail.ru
Поступила в редакцию 23.03.2020
Принята к публикации 29.05.2020
Аннотация
Статья посвящена проблеме обоснования корректности испытаний на прочность при растяжении плоских образцов из стекло-, углепластиков. Любой способ закрепления образца вызывает концентрацию напряжений и отрицательно влияет на прочность, и в статье даны количественные оценки этого эффекта. На основе упрощенного уравнения сдвигового анализа рассчитаны распределения напряжений в образцах при различных способах моделирования эпюры касательных напряжений, приложенных со стороны захватов. Преимущество аналитического решения состоит в том, что удается наглядно описать влияние на реализацию прочности: длины захватов и рабочей части, и, особенно, толщины образцов. Подобный масштабный эффект часто объясняют с позиции статистической теории прочности, но приведенный анализ показывает, что наблюдаемое снижение прочности с ростом толщины образца можно объяснить эффектом неоднородности поля напряжений вблизи захватов. Проявление этого краевого эффекта типа Сен-Венана особенно заметно у полимерных композитов, имеющих низкое (по сравнению с металлами) отношение межслойного модуля сдвига к продольному модулю Юнга.
Методы испытания однонаправленных композитов на растяжения потребовали многолетней отработки и стандартизации [1, 2]. Ни сверление, ни создание галтелей для подобных материалов недопустимы: при нагружении возникнут расщепления вдоль волокон [2, 3]. Поэтому стандартизованы испытания гладких прямоугольных образцов, для которых необходимо оценить влияние на прочность концентрации напряжений, и этой задаче посвящена настоящая статья.
Известно, что наилучшие результаты дает применение волокнистых композитов (стекло-, угле-, органопластиков) в тех деталях, в которых удается расположить волокна вдоль направлений главных напряжений [4–6]. Простейшими, но и наиболее удачными объектами применения почти однонаправленных композитов оказываются одномерно нагруженные изделия [7]. К ним можно отнести: стержни арматуры, шест для прыжков, лук, листовую рессору, лыжи и лыжные палки, складные телескопические удилища из углепластика, пултрузионные профили. Большой эффект дает оптимальное армирование цилиндрических сосудов давления, в которых основную нагрузку несут равнонапряженные армирующие волокна. Но как только геометрия детали или узла крепления становится более сложной, возникает концентрация напряжений и сложное (неодноосное) напряженное состояние, и традиционное прямолинейное армирование перестает быть эффективным [7–9]. В то же время, рекламные свойства полимерных композитов относят именно к однонаправленному армированию, на примере которого обосновывают преимущества композитов по удельным характеристикам (прочности и модулю упругости, отнесенным к удельному весу) в сравнении с традиционными стальными, алюминиевыми, титановыми сплавами.
Сложность создания узлов крепления в композитах из тканей или однонаправленных препрегов зачастую сводит на нет все преимущества композитов. Наряду с проблемой возникновения трудно обнаруживаемых дефектов типа расслоений и расщеплений [10, 11] проблемы создания узлов крепления без заметного снижения реализации прочности волокон оказываются основным сдерживающим фактором для расширения областей и эффективности применения композитов [12]. Таким образом, проектирование узлов крепления композитных деталей, наряду с совершенствованием методов расчета, оказывается не только фундаментальной, но и крайне важной прикладной проблемой технологической механики композитов [13, 14].
Традиционное сверление под заклепки или болты вызывает разрушение волокон и концентрацию напряжений [15], что приводит к снижению реализации прочности примерно в два раза. При уменьшении диаметра крепежных элементов, при использовании “игл”, “гвоздей” или прошивки проволокой эффективность соединения растёт, особенно если эти “гвозди” вводятся в соединение до полимеризации композита, и они раздвигают, а не разрывают волокна. Но подобные технологии недостаточно отработаны и пока не применяются в промышленных масштабах.
Клеевые соединения [16] по мере создания очень прочных и быстро твердеющих клеев казались предпочтительными, но в отличие от металлов у полимерных композитов проявляется отрицательный эффект низких межслойных прочности и модуля сдвига. Ситуация напоминает попытку разорвать книгу, прочно приклеив захваты к обложке. Передать нагрузку с обложки на все страницы не удается. Эффект Сен-Венана и размер зоны краевого эффекта зависят от отношения межслойного модуля сдвига к продольному модулю Юнга [17]. Для стекло- углепластиков это отношение намного ниже, чем для стали, и поэтому в зоне клеевого соединения возникает значительная концентрация напряжений в крайних слоях, затрудняющая эффективную передачу усилий на все сечение детали.
Основной вывод, следующий из малоудачных попыток перенести на композиты многолетний опыт работы с металлами, состоит в том, что надо идти другим путем. “Think composites”, как призывал известный ученый С. Цай (S. Tsai) – “думай композитами”. И наилучшим советчиком в области композитного проектирования могла бы стать живая Природа, за миллионы лет отбора реализовавшая принципы создания прочных, анизотропных материалов. Соединение ветви или корневой системы со стволом отличается от придуманных человечеством мест крепления (гвозди, шурупы, клей, “шип-паз”) тем, что природное соединение прочнее основного материала. Ветку можно сломать, но нельзя оторвать от ствола. Вот подобные биологические (bio-inspired – “навеянные Природой”) решения [18] являются наиболее перспективным и важным направлением в механике композитов. Немного перефразируя классиков (Бернарда Шоу, А.П. Чехова) можно сказать: “чем дольше я занимаюсь композитами, тем больше люблю древесину”.
Идея создания крепления, напоминающего сучок, долго носилась в воздухе. Развитие методов компьютерного моделирования (аналитические решения подобных задач неизвестны) привело к появлению большого числа работ, связанных с построением оптимальных траекторий волокон, обтекающих отверстие [19].
Но кроме крепления через отверстия существует целый класс других видов механических соединений. Человеческий опыт работы с древесиной привел к созданию очень прочных узлов крепления: топора к топорищу (расклинивание), кувалды к рукояти (насадка со стороны более тонкой части рукояти), оглобли к хомуту в конской упряжи (через ремни). Все эти виды крепления передают нагрузку через боковую поверхность, без сверления.
Анализу подобной схемы закрепления композитных образцов посвящена настоящая статья.
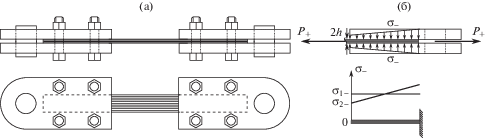
Способ крепления. Для испытаний на растяжение используются захваты (рис. 1), зажимающие плоский образец постоянным поперечным усилием Р–, распределенным по захватной части образца, которая имеет длину а и ширину w.
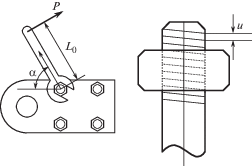
Поперечные усилия создаются четырьмя болтами при затяжке фиксированным моментом М = РL0 (рис. 2). Сила Р для создания необходимого момента затяжки, зависит от длины плеча L0, но с помощью динамометрического ключа можно непосредственно определять приложенный момент. При повороте ключа на угол $\alpha $ мы совершаем работу $А = \alpha M$.
Такую же работу без учета потерь на трение совершает гайка при перемещении на долю $\alpha {\text{/}}2\pi $ от шага u резьбы (например, u = 1.5 мм для используемых в захватах гаек М10). Поперечное усилие, которое создадут четыре болта, из “золотого правила механики” выражается в виде
При приложении растягивающего усилия ${{P}_{ + }}$ касательные напряжения на поверхности образца в захватах растут вплоть до разрушения или до возникновения проскальзывания, при котором реализуется явление типа сухого трения. Согласно “закону” (гипотезе) Кулона сила трения при начале скольжения пропорциональна нормальному давлению и не зависит от площади поверхности трения. На самом деле, конечно, она зависит от всего: и от площади контакта, и от шероховатости поверхности, и от силы давления, но подобной нелинейностью обычно пренебрегают. Будем считать, что предельное продольное усилие типа силы трения пропорционально поперечному усилию, и коэффициент пропорциональности назовем условным коэффициентом трения. Почему условным? Потому что это не просто трение, а результат метода крепления, использующего для сцепления двухстороннюю шкурку между металлом и композитным образцом. Происходит нелинейное внедрение абразивных частиц в металл – и на уровне физики этот процесс разрушения-проскальзывания описывается очень сложно. Но механика моделирует всю эту сложность простейшей гипотезой Кулона, которая служит основой инженерных расчетов.
Определение условного коэффициента трения возможно в результате простого эксперимента. Для фиксированного поперечного усилия (момента затяжки болтов) определяют, при каком продольном усилии произойдет проскальзывание (вытаскивание образца из захватов). Разделив продольное усилие ${{P}_{ + }}$ при начале проскальзывания на поперечную силу ${{P}_{ - }}$, можно определить условный коэффициент трения $k = \frac{{{{P}_{ + }}}}{{{{P}_{ - }}}}.$
Считая касательные напряжения равномерно распределенными на двух участках поверхности образца с общей площадью $2aw$, можно оценить их среднее значение по простейшей формуле ${{\tau }_{1}}$ = $\frac{{{{P}_{ + }}}}{{aw}}$ = $\frac{{k{{P}_{ - }}}}{{aw}}$ = $\frac{{2\sigma _{x}^{ + }h}}{a}$.
Индекс “+” относится к растягивающей продольной силе, индекс “–” к поперечной сжимающей силе (рис. 1б).
При стандартных размерах сечения рабочей части $2h = 3$ мм; $w = 10$ мм, прочности $\sigma _{x}^{{ + * }} = 1000$ МПа предельное продольное усилие составит 30 000 Н, и при условном коэффициенте трения, равном единице, можно оценить поперечное усилие и необходимый момент затяжки болтов M = 30/16.7 ≈ 1.8 Н × м. Сжимающие напряжения в захватах при нагрузке ${{P}_{ - }} = 3 \times {{10}^{4}}$ Н и длине захватов а = 50 мм составляют ${{\sigma }_{ - }}$ = 60 МПа ≈ 6 кг/мм2, что вполне допустимо по условию поперечной прочности. При ${{P}_{ - }} \approx {{P}_{ + }} \Rightarrow {{\tau }_{1}}$ = ${{{{\sigma }_{ - }}} \mathord{\left/ {\vphantom {{{{\sigma }_{ - }}} 2}} \right. \kern-0em} 2}$ = 30 МПа.
Допустимый момент затяжки необходимо оценивать опытным путем: сверху – по прочности образца на поперечное сжатие, и снизу – по исключению проскальзывания. Условия закрепления можно оптимизировать, подбирая отношение моментов затяжки болтов в каждом ряду захвата, что количественно описано ниже (случай 2).
Расчет напряжений в прямоугольной полосе. По модели упрощенного сдвигового анализа рассмотрена задача об одноосном растяжении слоистого композита, состоящего из чередующихся тонких слоев: жестких волокон, воспринимающих (только и все) растягивающие напряжения, и мягкой матрицы, сопротивляющейся лишь сдвигу. Для такой модели композитного материала уравнение равновесия 2-го порядка в перемещениях имеет вид [20]
(1)
$\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} + {{\beta }^{2}}\frac{{{{\partial }^{2}}u}}{{\partial {{y}^{2}}}} = 0,\quad {\text{где}}\quad {{\beta }^{2}} = \frac{{{{G}_{{xy}}}}}{{{{E}_{x}}}}.$Решение уравнения (1) ищется методом разделения переменных, и, из соображений симметрии, имеет вид
(2)
$u\left( {x,y} \right) = \sum\limits_{n = 1}^\infty {{{X}_{n}}} \left( x \right){{Y}_{n}}\left( y \right) = \sum\limits_{n = 1}^\infty {{{A}_{n}}\sin \frac{{n\pi x}}{L}\operatorname{ch} \frac{{n\pi y}}{{\beta L}}} .$Касательное и нормальное напряжения из (2) и закона Гука выразятся в виде
(3)
${{\tau }_{{xy}}}\left( {x,y} \right) = {{G}_{{xy}}}\frac{{\partial {{u}_{x}}}}{{\partial y}} = {{G}_{{xy}}}\frac{\pi }{{\beta L}}\sum\limits_{n = 1}^\infty {\left( {n{{A}_{n}}\sin \frac{{n\pi x}}{L}\operatorname{sh} \frac{{n\pi y}}{{\beta L}}} \right)} ;$(4)
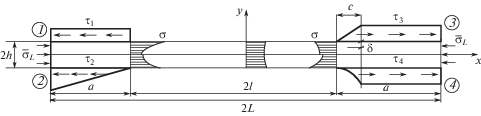
${{\sigma }_{x}} = {{E}_{x}}\frac{{\partial {{u}_{x}}}}{{\partial x}} = \frac{{\pi {{E}_{x}}}}{L}\sum\limits_{n = 1}^\infty {\left( {n{{A}_{n}}\cos \frac{{n\pi x}}{L}\operatorname{ch} \frac{{n\pi y}}{{\beta L}}} \right)} .$Получим расчетные формулы для четырех случаев: 1) равномерная эпюра касательных напряжений; 2) линейная эпюра; 3) частично линейная; 4) частично параболическая (с нулевой производной у края захватов) (рис. 3).
Рис. 3.
Схемы нагружения образца при растяжении с четырьмя видами эпюр 1, 2, 3, 4 касательных напряжений в захватной части образца.
Случай 1. На части боковой поверхности (в захватах) задано равномерное распределение напряжений (рис. 3, позиция 1)
(5)
${{\tau }_{{xy}}}{{{\text{|}}}_{{y = \pm h}}} = {{\varphi }_{1}}(x) = \left\{ \begin{gathered} 0,\quad {\text{при}}\quad 0 < \left| x \right| \leqslant l = L - a \hfill \\ {{\tau }_{1}} = \frac{{\bar {\sigma }h}}{a},\quad {\text{при}}\quad l < \left| x \right| \leqslant L \hfill \\ \end{gathered} \right\}.$Чтобы найти коэффициенты ${{A}_{{n1}}}$, надо умножить правую и левую части равенства (5) с подстановкой (3) на $sin\frac{{m\pi x}}{L}$ и проинтегрировать по х от –L до L. Известно и легко проверить, что
(6)
$\int\limits_{ - L}^L {sin\frac{{n\pi x}}{L}sin\frac{{m\pi x}}{L}dx = } \left\{ {\begin{array}{*{20}{c}} {L\quad {\text{при}}\quad m = n} \\ {0\quad {\text{при}}\quad m \ne n} \end{array}} \right\}.$В результате из граничного условия (5) и соотношения (3) с учетом (6) определим числовые коэффициенты рядов (2)–(4), выразив их через среднее напряжение $\bar {\sigma }$ в рабочей части образца (например, при х = 0)
(7)
$\begin{gathered} {{G}_{{xy}}}\frac{{n\pi }}{{\beta L}}{{A}_{{n1}}}\operatorname{sh} \frac{{n\pi h}}{{\beta L}}\int\limits_0^L {{{{\sin }}^{2}}\frac{{n\pi x}}{L}dx} = \int\limits_0^L {{{\varphi }_{1}}\left( x \right)\sin \frac{{n\pi x}}{L}dx} = {{\tau }_{1}}\int\limits_l^L {\sin \frac{{n\pi x}}{L}dx} \Rightarrow \\ \Rightarrow {{A}_{n}}_{1} = \frac{{2L{{\tau }_{1}}\beta }}{{{{G}_{{xy}}}{{n}^{2}}{{\pi }^{2}}\operatorname{sh} \frac{{n\pi h}}{{\beta L}}}}\left( {\cos \frac{{n\pi l}}{L} - \cos n\pi } \right) = \frac{{2L\bar {\sigma }\beta h\cos n\pi }}{{a{{G}_{{xy}}}{{n}^{2}}{{\pi }^{2}}\operatorname{sh} \frac{{n\pi h}}{{\beta L}}}}\left( {\cos \frac{{n\pi a}}{L} - 1} \right). \\ \end{gathered} $Подставляя (7) в (4), с учетом $\beta = \sqrt {{{{{G}_{{xy}}}} \mathord{\left/ {\vphantom {{{{G}_{{xy}}}} {{{E}_{x}}}}} \right. \kern-0em} {{{E}_{x}}}}} $ найдем распределение нормальных напряжений, удовлетворяющее одному граничному условию (5)
(8)
$\begin{gathered} {{\sigma }_{{x1}}} = \frac{{2\bar {\sigma }h}}{{\pi \beta a}}\sum\limits_{n = 1}^\infty {\frac{1}{n}\left[ {{{T}_{1}}} \right]cos\frac{{n\pi x}}{L}} \left\{ {{{H}_{y}}} \right\}, \\ \left[ {{{T}_{1}}} \right] = \left( {\cos \frac{{n\pi a}}{L} - 1} \right)\cos n\pi ,\quad \left\{ {{{H}_{y}}} \right\} = ch\frac{{n\pi y}}{{\beta L}}{\text{/}}sh\frac{{n\pi h}}{{\beta L}}. \\ \end{gathered} $Чтобы удовлетворить (в среднем) второму граничному условию отсутствия напряжений на торцах образца $x = \pm L$, нужно добавить к решению (8) с обратным знаком среднее на торцах напряжение $\bar {\sigma }{}_{{L1}}$, полученное из (8)
(10)
${{\bar {\sigma }}_{{L1}}} = \frac{1}{h}\int\limits_0^h {{{{\left. {{{\sigma }_{{x1}}}} \right|}}_{{x = L}}}} dy = \frac{{2\bar {\sigma }L}}{{{{\pi }^{2}}a}}\sum\limits_{n = 1}^\infty {\frac{1}{{{{n}^{2}}}}\left[ {{{T}_{1}}} \right]\cos n\pi } = - \bar {\sigma }\left( {1 - \frac{a}{{2L}}} \right).$Среднее напряжение в рабочей части легко получить интегрированием (9) при х = 0 с применением тождеств (12)
(11)
$\bar {\sigma } = \frac{1}{h}\int\limits_0^h {{{{\left. {\sigma _{{x1}}^{ + }} \right|}}_{{x = 0}}}} dy = \frac{{{{\tau }_{1}}a}}{h}.$При вычислении средних напряжений в середине (11) и на торце образца (10) используются известные выражения
(12)
$\sum\limits_{n = 1}^\infty {{{{( - 1)}}^{{n + 1}}}\frac{{\cos n\alpha }}{{{{n}^{2}}}}} = \frac{{{{\pi }^{2}}}}{{12}} - \frac{{{{\alpha }^{2}}}}{4},\quad \sum\limits_{n = 1}^\infty {\frac{{\cos n\alpha }}{{{{n}^{2}}}}} = \frac{{{{\pi }^{2}}}}{6} - \frac{{\pi \alpha }}{2} + \frac{{{{\alpha }^{2}}}}{4}.$Оценка влияния концентрации напряжений в захватах на реализацию прочности. По формулам (8)–(12) можно оценить концентрацию напряжений через отношение локального напряжения $\sigma _{{x1}}^{ + }$ к среднему $\bar {\sigma }$. Теоретическим коэффициентом концентрации напряжений (“stress concentration factor”) называют отношение наибольшего напряжения к среднему. Наибольшее напряжение достигается у края захватов при $x = \pm l$, $y = \pm h$ (в данной постановке напряжение у края захватов обращается в бесконечность, т.к. ряд (8) в этой точке расходится, как гармонический). Тут важен анализ, так как при численной реализации сумма гармонического ряда растет крайне медленно: чтобы эта сумма достигла значения 100, нужно взять безумное число 1047 членов.
Ситуация напоминает парадокс сингулярной теории упругости в линейной механике разрушения: напряжения в вершине трещины обращаются в бесконечность, но энергия, поступающая в вершину трещины, конечна. Один из традиционных подходов, позволяющих обойти этот парадокс, состоит в использовании не максимального, а некоторого эффективного напряжения ${{\sigma }_{{\operatorname{eff} }}}\left( \delta \right)$, выражаемого через интеграл от напряжений по некоторому характерному размеру $\delta $ (“mean stress criterion”)
(13)
${{\sigma }_{{\operatorname{eff} }}}\left( \delta \right) = \frac{1}{\delta }\int\limits_{h - \delta }^h {{\left. {\sigma _{x}^{ + }} \right|}_{{x = l}}}dy.$Еще более простой, но фактически эквивалентный результат можно получить, вычисляя эффективное напряжение ${{\sigma }_{{\operatorname{eff} }}}\left( {{{\delta }_{1}}} \right)$ в сечении $x = L - a = l$ на некотором характерном (феноменологическом) расстоянии ${{\delta }_{1}} < \delta $ от сингулярной точки при $y = h - {{\delta }_{1}}$, и это расстояние (свойство материала) определяется из условия наилучшего согласия с экспериментом. Для оценки феноменологического параметра ${{\delta }_{1}}$ необходимо сравнить результаты приведенных ниже расчетов эффективного коэффициента концентрации напряжений с экспериментами по определению прочности на образцах различной толщины.
Эффективное напряжение оказывается конечным в отличие от напряжения при $x = l$; $y = h$, так как ряд (8) для эффективного напряжения по этой гипотезе (“point-stress criterion”) сходится и имеет вид
(14)
$\begin{gathered} {{\sigma }_{{\operatorname{eff} 1}}} = \sigma _{{x1}}^{ + }\left| {_{{y = h - {{\delta }_{1}}}}} \right. = \frac{{2\bar {\sigma }h}}{{\pi \beta a}}\sum\limits_{n = 1}^\infty {\frac{1}{n}\left[ {{{T}_{1}}} \right]\left\{ {{{H}_{1}}} \right\}\cos \frac{{n\pi l}}{L}} + \bar {\sigma }\left( {1 - \frac{a}{{2L}}} \right), \\ \left\{ {{{H}_{1}}} \right\} = \operatorname{ch} \frac{{n\pi \left( {h - {{\delta }_{1}}} \right)}}{{\beta L}}{\text{/}}\operatorname{sh} \frac{{n\pi h}}{{\beta L}}. \\ \end{gathered} $Были проведены численные сравнения расчетов по формулам (13) и (14), соответствующим различным выражениям для эффективных напряжений. Качественно зависимости оказываются сходными, поэтому на приведенных ниже графиках отражены только расчеты по формулам типа (14), соответствующим второй гипотезе (“point-stress criterion”).
В (14) и ниже квадратными скобками выделена тригонометрическая часть $\left[ {{{T}_{1}}} \right]$ – различная для случаев 1–4, и фигурными скобками гиперболическая часть $\left\{ {{{H}_{1}}} \right\}$ – одинаковая для всех случаев 1–4.
Теперь эффективный коэффициент концентрации напряжений – коэффициент снижения прочности (“strength reduction factor”) можно вычислить, относя “эффективное” напряжение (14) (или (13)) к среднему (11)
(15)
${{K}_{{\sigma 1}}} = \frac{{{{\sigma }_{{\operatorname{eff} }}}\left( {{{\delta }_{1}}} \right)}}{{\bar {\sigma }}}.$Для реальных, стандартных размеров образцов и захватов $a$ = l = L/2 = 50 мм тригонометрическая часть $\left[ {{{T}_{1}}} \right]$ в (14) существенно упрощается: отличными от нуля остаются только члены с номерами n = 2, 6, 10, …, и все они равны двум. Сложное выражение (14), (15) с заменой $n = 4k + 2$, например, при ${{\delta }_{1}}$ = 1 мм, $\beta = 0.2$ приобретает вид
(16)
${{K}_{{\sigma 1}}} = 0.75 + 0.382\sum\limits_{k = 0}^\infty {\frac{1}{{4k + 2}}\left\{ {\frac{{\operatorname{ch} \left[ {0.314\left( {4k + 2} \right)} \right]}}{{\operatorname{sh} \left[ {0.471\left( {4k + 2} \right)} \right]}}} \right\}} .$“Гиперболический” сомножитель $\left\{ {{{H}_{1}}} \right\}$ в фигурных скобках в (14), (16) стремится к нулю, поэтому гармонический ряд ${1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0em} n}$ с таким сомножителем – сходится
(17)
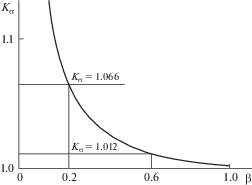
$\left\{ {{{H}_{1}}} \right\} = \frac{{ch\left( {0.1n\pi } \right)}}{{sh\left( {0.15n\pi } \right)}}\;\xrightarrow[{n \to \infty }]{}\;\frac{{exp\left( {0.1n\pi } \right)}}{{exp\left( {0.15n\pi } \right)}} = \frac{1}{{exp\left( {0.05n\pi } \right)}} \approx {{0.85}^{n}}\;\xrightarrow[{n \to \infty }]{}\;0.$В (16)–(18) для композитных образцов условно принято: продольный модуль Юнга ${{Е}_{x}} = 80$ ГПа, межслойный модуль сдвига ${{G}_{{xy}}} \approx 3.2$ ГПа, поэтому $\beta $ = $\sqrt {{{{{G}_{{xy}}}} \mathord{\left/ {\vphantom {{{{G}_{{xy}}}} {{{E}_{x}}}}} \right. \kern-0em} {{{E}_{x}}}}} = 0.2$. Для изотропных металлов, например, для стали $\beta $ = $\sqrt {{G \mathord{\left/ {\vphantom {G E}} \right. \kern-0em} E}} $ = $\sqrt {{1 \mathord{\left/ {\vphantom {1 {\left[ {2\left( {1 + \nu } \right)} \right]}}} \right. \kern-0em} {\left[ {2\left( {1 + \nu } \right)} \right]}}} $ ≈ 0.6 (рис. 4). Для построения большинства графиков брались за основу следующие характеристики: a = 50 мм, c = 0.1a, 2h = 6 мм, L = 100 мм, l = 50 мм, β = 0.2.
Рис. 4.
Зависимость эффективного коэффициента концентрации напряжений ${{K}_{\sigma }}$ от упругих свойств материала $\beta $. Представлена кривая для расчетного случая 1, кривые для остальных случаев принципиально не отличаются.
Если рассчитывать эффективный коэффициент концентрации напряжений ближе к краю захвата, например, при ${{\delta }_{1}} = 0.2$ мм, то расчетная формула (16) примет вид
(18)
${{K}_{{\sigma 1}}} \approx 0.75 + 0.382\sum\limits_{k = 0}^{10} {\frac{1}{{4k + 2}}\left\{ {\frac{{ch\left[ {0.44\left( {4k + 2} \right)} \right]}}{{sh\left[ {0.471\left( {4k + 2} \right)} \right]}}} \right\}} .$Все приведенные графики (рис. 4–9) построены в приложении для инженерных расчетов MathCad по общим формулам типа (14), а наглядные формулы (16), (18) нужны лишь для проверки символьных вычислений.
Рис. 5.
Зависимость коэффициента концентрации ${{K}_{\sigma }}$ от ${{\delta }_{1}}$ для различных расчетных случаев, номера кривых соответствуют нумерации расчетных случаев.
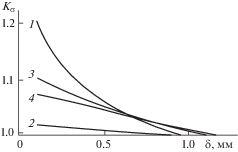
Рис. 6.
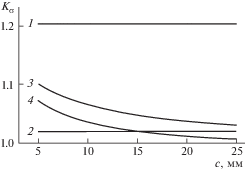
Зависимости коэффициента снижения прочности ${{K}_{\sigma }}$ от длины захватной части для образцов с одинаковой толщиной и длиной рабочей зоны.
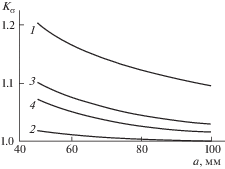
Рис. 7.
Зависимости коэффициента снижения прочности ${{K}_{\sigma }}$ от длины рабочей зоны для образцов одинаковой толщиной и длиной захватной части.
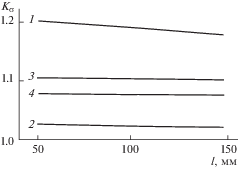
Рис. 8.
Зависимости коэффициента снижения прочности ${{K}_{\sigma }}$ от толщины образца при прочих одинаковых параметрах.
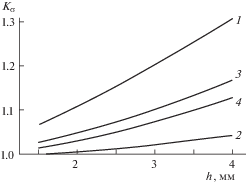
Рис. 9.
Зависимости коэффициента снижения прочности ${{K}_{\sigma }}$ от длины c сглаженной части захватов.
Случай 2. Путем неравномерной затяжки болтов можно добиться, чтобы ближе к рабочей части поперечные напряжение и смещение стали меньше, чем на конце образца (рис. 1б). В этом случае для простоты эпюру изменения касательных напряжений ${{\tau }_{{xy}}}\left( x \right)$ в захвате можно считать линейной (рис. 3, позиция 2) и задать по аналогии с (5) на поверхности образца
(19)
${{\tau }_{{xy}}}{{{\text{|}}}_{{y = \pm h}}} = {{\varphi }_{2}}(x) = \left\{ {\begin{array}{*{20}{c}} {0,\quad при\quad 0 < {\text{|}}x{\text{|}} < l = L - a} \\ {{{\tau }_{2}}\frac{{x - l}}{a},\quad при\quad l < {\text{|}}x{\text{|}} < L} \end{array}} \right\};\quad {{\tau }_{2}} = 2{{\tau }_{1}} = 2\frac{{\bar {\sigma }h}}{a}.$Для сравнения коэффициентов концентрации напряжений во всех случаях 1–4 будем считать одинаковым среднее напряжение $\bar {\sigma }$, что соответствует одинаковой растягивающей нагрузке ${{P}_{ + }} = 2\bar {\sigma }hw$.
Рассчитаем для граничного условия (19) коэффициенты ${{A}_{{n2}}}$ в (2)–(4) по соотношению (7) с учетом (6)
(20)
$\begin{gathered} \int\limits_0^L {{{\varphi }_{2}}\left( x \right)} \sin \frac{{n\pi x}}{L}dx = {{A}_{{n2}}}\frac{{n\pi }}{{\beta L}}{{G}_{{xy}}}\operatorname{sh} \frac{{n\pi h}}{{\beta L}}\int\limits_0^L {{{{\sin }}^{2}}\frac{{n\pi x}}{L}dx} = {{A}_{{n2}}}\frac{{n\pi }}{{2\beta }}{{G}_{{xy}}}\operatorname{sh} \frac{{n\pi h}}{{\beta L}}, \\ {{\tau }_{2}}\left[ {\int\limits_l^L {\frac{{x - l}}{a}} \sin \frac{{n\pi x}}{L}dx} \right] = \frac{{{{\tau }_{2}}L}}{{n\pi }}\left[ { - \cos n\pi + \frac{L}{{n\pi a}}\left( {\sin n\pi - \sin \frac{{n\pi l}}{L}} \right)} \right] = \frac{{{{\tau }_{2}}L}}{{n\pi }}\left[ {{{T}_{2}}} \right]; \\ {{A}_{{n2}}} = \frac{{2{{\tau }_{2}}L\beta }}{{{{G}_{{xy}}}{{n}^{2}}{{\pi }^{2}}}}\left[ {{{T}_{2}}} \right]{\text{/}}\operatorname{sh} \frac{{n\pi h}}{{\beta L}};\quad \left[ {{{T}_{2}}} \right] = \cos n\pi \left( {\frac{L}{{n\pi a}}\sin \frac{{n\pi a}}{L} - 1} \right). \\ \end{gathered} $Распределение напряжений по аналогии с (8) примет вид
(21)
$\begin{gathered} {{\sigma }_{{x2}}} = \frac{{4\bar {\sigma }h}}{{\pi \beta a}}\sum\limits_{n = 1}^\infty {\frac{1}{n}\left[ {{{T}_{2}}} \right]\left\{ {{{H}_{y}}} \right\}cos\frac{{n\pi x}}{L},} \\ {{\sigma }_{{\operatorname{eff} 2}}} = \frac{{4\bar {\sigma }h}}{{\pi \beta a}}\sum\limits_{n = 1}^\infty {\frac{1}{n}\left[ {{{T}_{2}}} \right]\left\{ {{{H}_{1}}} \right\}cos\frac{{n\pi l}}{L}} - {{{\bar {\sigma }}}_{{L2}}}. \\ \end{gathered} $Среднее напряжение на торце рассчитывается с помощью (21)
(22)
$\begin{gathered} {{{\bar {\sigma }}}_{{L2}}} = \frac{1}{h}\int\limits_0^h {{{{\left. {{{\sigma }_{{x2}}}} \right|}}_{{x = L}}}} dy = \frac{1}{h}\sum\limits_{n = 1}^\infty {\frac{{2{{\tau }_{2}}}}{{\beta n\pi }}\left[ {{{T}_{2}}} \right]\cos n\pi \frac{{\beta L}}{{n\pi }}} = \frac{{4\bar {\sigma }L}}{{{{\pi }^{2}}a}}\sum\limits_{n = 1}^\infty {\frac{1}{{{{n}^{2}}}}\left( {\frac{L}{{n\pi a}}\sin \frac{{n\pi a}}{L} - 1} \right)} , \\ {{K}_{{\sigma 2}}} = \frac{{{{\sigma }_{{\operatorname{eff} 2}}}\left( {{{\delta }_{1}}} \right)}}{{\bar {\sigma }}}. \\ \end{gathered} $Среднее напряжение в рабочей части при х = 0 из (21) по аналогии с (22) выражается в виде
(23)
$\bar {\sigma } = \frac{1}{h}\int\limits_0^h {{{{\left. {\sigma _{{x2}}^{{}}} \right|}}_{{x = 0}}}} dy - {{\bar {\sigma }}_{{L2}}} = \frac{{{{\tau }_{2}}a}}{{2h}}.$Воспользоваться соотношениями типа (12) для аналитического решения (22), (23) не удается, так как для ряда, включающего синус и третью степень ${1 \mathord{\left/ {\vphantom {1 {{{n}^{3}}}}} \right. \kern-0em} {{{n}^{3}}}}$, аналитические выражения авторам неизвестны, но численные расчеты не представляют сложности.
Случай 3. Снижению концентрации напряжений способствует сглаживание кромок захватов, что исключает скачкообразный рост приложенных касательных напряжений. Для численного анализа такой схемы нагружения следует, как показано на рис. 3 (позиция 3), задать изменение касательных напряжений ${{\tau }_{{xy}}}$ на поверхности образца по аналогии с (5), (19) в виде
(24)
${{\tau }_{{xy}}}{{{\text{|}}}_{{y = \pm h}}} = {{\varphi }_{3}}\left( x \right) = \left\{ {\begin{array}{*{20}{c}} {0,\quad при\quad 0 < {\text{|}}x{\text{|}} < l = L - a} \\ {{{\tau }_{3}}\frac{{x - l}}{c},\quad при\quad l < {\text{|}}x{\text{|}} < l + c} \\ {{{\tau }_{3}} = \frac{{\bar {\sigma }h}}{{a - {c \mathord{\left/ {\vphantom {c 2}} \right. \kern-0em} 2}}},\quad при\quad l + c < {\text{|}}x{\text{|}} < L} \end{array}} \right\}.$Для эпюры (24) коэффициенты ${{A}_{{n3}}}$ в рядах (2)–(4) вычисляются аналогично случаям 1 и 2. Далее через новое выражение для напряжений ${{\sigma }_{{x3}}}$ вида (21) рассчитывается по формуле (10) среднее напряжение на торце ${{\bar {\sigma }}_{{L3}}}$, и в результате получаем
(25)
$\begin{gathered} {{\sigma }_{{\operatorname{eff} 3}}} = \frac{{2\bar {\sigma }h}}{{\pi \beta \left( {a - c{\text{/}}2} \right)}}\sum\limits_{n = 1}^\infty {\frac{1}{n}\left[ {{{T}_{3}}} \right]\left\{ {{{H}_{1}}} \right\}\cos \frac{{n\pi l}}{L}} - {{{\bar {\sigma }}}_{{L3}}}, \\ \left[ {{{T}_{3}}} \right] = \frac{L}{{n\pi c}}\left( {\sin \frac{{n\pi \left( {l + c} \right)}}{L} - \sin \frac{{n\pi l}}{L}} \right) - \cos n\pi , \\ \bar {\sigma } = {{\tau }_{3}}\frac{{2a - c}}{{2h}},\quad {{K}_{{\sigma 3}}} = \frac{{{{\sigma }_{{\operatorname{eff} 3}}}\left( {{{\delta }_{1}}} \right)}}{{\bar {\sigma }}}. \\ \end{gathered} $При с = а тригонометрическая часть $\left[ {{{T}_{3}}} \right]$ в (25) совпадает с $\left[ {{{T}_{2}}} \right]$ (21) – случай 2, а при $с \to 0$ можно предельным переходом показать, что $\left[ {{{T}_{3}}} \right]$ переходит в выражение $\left[ {{{T}_{1}}} \right]$ из (8) – случай 1.
Случай 4. Плавную передачу усилий от захватов на образец можно смоделировать гладкой эпюрой с нулевой производной у кромки захвата (рис. 3, позиция 4). Для численного анализа распределения напряжений в этом случае можно задать на поверхности образца по аналогии с (24) параболическое изменение касательных напряжений ${{\tau }_{{xy}}}\left( x \right)$ на начальном участке захватов
(26)
${{\tau }_{{xy}}}{{{\text{|}}}_{{y = \pm h}}} = {{\varphi }_{4}}\left( x \right) = \left\{ {\begin{array}{*{20}{c}} {0,\quad {\text{при}}\quad 0 < {\text{|}}x{\text{|}} < l = L - a} \\ {{{\tau }_{4}}\frac{{{{{\left( {x - l} \right)}}^{2}}}}{{{{с}^{2}}}},\quad {\text{при}}\quad l < {\text{|}}x{\text{|}} < l + c} \\ {{{\tau }_{4}} = \frac{{\bar {\sigma }h}}{{a - {{2c} \mathord{\left/ {\vphantom {{2c} 3}} \right. \kern-0em} 3}}},\quad {\text{при}}\quad l + c < {\text{|}}x{\text{|}} < L} \end{array}} \right\}.$Для эпюры (26) по аналогии со случаем эпюры (24) можно рассчитать коэффициенты ${{A}_{{n4}}}$ в решении (4)
(27)
$\begin{gathered} {{A}_{{n4}}} = {{I}_{{n4}}}\frac{{2\beta }}{{n\pi {{G}_{{xy}}}}}{\text{/}}\operatorname{sh} \frac{{n\pi h}}{{\beta L}}~{{I}_{{n4}}} = {{\tau }_{4}}\left[ {\int\limits_l^{l + c} {{{{\left( {\frac{{x - l}}{c}} \right)}}^{2}}} sin\frac{{n\pi x}}{L}dx + \int\limits_{l + c}^L {sin\frac{{n\pi x}}{L}dx} } \right] = \frac{{{{\tau }_{4}}L}}{{n\pi }}\left[ {{{T}_{4}}} \right], \\ \left[ {{{T}_{4}}} \right] = \frac{{2L}}{{n\pi c}}\sin \frac{{n\pi \left( {l + c} \right)}}{L} + \frac{{2{{L}^{2}}}}{{{{n}^{2}}{{\pi }^{2}}{{c}^{2}}}}\left( {\cos \frac{{n\pi \left( {l + c} \right)}}{L} - \cos \frac{{n\pi l}}{L}} \right) - \cos n\pi . \\ \end{gathered} $Далее проводятся расчеты по формулам (8)–(11) или (21), (23) с использованием в (23) другого выражения для среднего напряжения
(28)
$\begin{gathered} \bar {\sigma } = \frac{{{{\tau }_{4}}}}{h}\left[ {\int\limits_l^{l + c} {{{{\left( {\frac{{x - l}}{c}} \right)}}^{2}}} dx + a - c} \right] = \frac{{{{\tau }_{4}}}}{h}\left( {a - \frac{{2c}}{3}} \right), \\ {{\sigma }_{{x4}}} = \frac{{2\bar {\sigma }h}}{{\pi \beta \left( {a - {{2c} \mathord{\left/ {\vphantom {{2c} 3}} \right. \kern-0em} 3}} \right)}}\sum\limits_{n = 1}^\infty {\left( {\frac{1}{n}\left[ {{{T}_{4}}} \right]\left\{ {{{H}_{y}}} \right\}\cos \frac{{n\pi x}}{L}} \right)} . \\ \end{gathered} $В результате получаем выражение для коэффициента снижения прочности
(29)
${{K}_{{\sigma 4}}} = \frac{{{{\sigma }_{{\operatorname{eff} 4}}}\left( {{{\delta }_{1}}} \right)}}{{\bar {\sigma }}} = \frac{{2h}}{{\pi \beta \left( {a - {{2c} \mathord{\left/ {\vphantom {{2c} 3}} \right. \kern-0em} 3}} \right)}}\sum\limits_{n = 1}^\infty {\frac{1}{n}\left[ {{{T}_{4}}} \right]\left\{ {{{H}_{1}}} \right\}cos\frac{{n\pi l}}{L}} - \frac{{{{{\bar {\sigma }}}_{{L4}}}}}{{\bar {\sigma }}}.$Выражение $\left[ {{{T}_{4}}} \right]$ в (27) и (29) можно проанализировать, положив $n\pi {l \mathord{\left/ {\vphantom {l L}} \right. \kern-0em} L} = b$, $n\pi {c \mathord{\left/ {\vphantom {c L}} \right. \kern-0em} L} = \varepsilon \to 0$. Тогда $\left[ {{{T}_{4}}} \right]$ стремится к выражению $\left[ {{{T}_{1}}} \right]$ из (8) для случая 1
(30)
$\begin{gathered} \left[ {{{T}_{4}}} \right] = 2\frac{{\sin b\cos \varepsilon + \sin \varepsilon \cos b}}{\varepsilon } + 2\frac{{\cos b\cos \varepsilon - \sin b\sin \varepsilon - \cos b}}{{{{\varepsilon }^{2}}}} - \\ - \;\cos n\pi \;\xrightarrow[{\varepsilon \to 0}]{}\;2\sin b{\text{/}}\varepsilon + 2\cos b - \cos b - 2\sin b{\text{/}}\varepsilon - \cos n\pi = \\ = \cos b - \cos n\pi = \left( {\cos \frac{{n\pi a}}{L} - 1} \right)\cos n\pi = \left[ {{{T}_{1}}} \right]. \\ \end{gathered} $Расчеты по формулам (25) и (29) показывают, что сглаживание (рис. 3, позиция 4) или снижение угла эпюры (рис. 3, позиция 3) приложенных касательных напряжений приводит к уменьшению КСП (коэффициента снижения прочности), который убывает с ростом длины с сглаженного участка. Результаты расчетов приведены на рис. 6–9, на которых нумерация кривых соответствует номерам расчетных случаев в статье.
Выводы. Способы снижения концентрации напряжений. Расчеты по рассмотренным моделям показывают, что влияние концентрации напряжений может быть снижено различными способами: 1. Уменьшением толщины образца; 2. Ростом длины рабочей зоны и длины захватов; 3. Увеличением межслойного модуля сдвига композита; 4. Неравномерной затяжкой болтов, создающей линейную эпюру напряжений в захватах; 5. Сглаживанием касательных напряжений у кромки захватов.
Эффективность всех этих способов получила в результате расчетов не только качественную, но и количественную оценку.
Список литературы
Портнов Г.Г., Кулаков В.Л., Арнаутов А.К. Особенности испытания высокопрочных однонаправленных композитов при одноосном растяжении // Пластические массы. 2008. № 4. С. 40.
Shokrieh M.M., Omidi M.J. Tension behavior of unidirectional glass/epoxy composites under different strain rates // Composite Structures. 2009. V. 88. № 4. P. 595.
Бабушкин А.В., Вильдеман В.Э., Лобанов Д.С. Испытания на растяжение однонаправленного высоконаполненного стеклопластика при нормальных и повышенных температурах // Заводская лаборатория. Диагностика материалов. 2010. Т. 76. № 7. С. 57.
Chen Ya., Zhao Yu., He Ch., Ai Sh., Lei H., Tang L., Fang D. Yield and failure theory for unidirectional polymer-matrix composites // Composites Part B: Engineering. 2019. V. 164. № 1. P. 612.
Боровков А.И., Мамчиц Д.В., Немов А.С., Новокшенов А.Д. Задачи моделирования и оптимизации панелей переменной жесткости и конструкций из слоистых композитов // Известия Российской академии наук. Механика твердого тела. 2018. № 1. С. 113.
Borovkov A.I., Mamchits D.V., Nemov A.S., Novokshenov A.D. Problems of modeling and optimization of variable-hardness panels and structures made of layered composites // Mechanics of Solids. 2018. V. 53. № 1. P. 93.
Полилов А.Н., Татусь Н.А., Плитов И.С. Оценка влияния разориентации волокон на жесткость и прочность профилированных композитных элементов // Проблемы машиностроения и надежности машин. 2013. № 5. С. 58.
Polilov A.N., Tatus N.A., Plitov I.S. Estimating the effect of misorientation of fibers on stiffness and strength of profiled composite elements // Journal of Machinery Manufacture and Reliability. 2013. V. 42. № 5. P. 390.
Полатов А.М. Компьютерное моделирование влияния концентратора напряжений на деформирование волокнистых материалов // Механика композиционных материалов и конструкций. 2017. Т. 23. № 3. С. 391.
Дедков Д.В., Зайцев А.В., Ташкинов А.А. Концентрация напряжений в слое тканого композита с закрытыми внутренними технологическими порами // Вестник Пермского государственного технического университета. Механика. 2011. № 4. С. 29.
Hu P., Pulungan D., Tao R., Lubineau G. An experimental study on the influence of intralaminar damage on interlaminar delamination properties of laminated composites // Composites Part A: Applied Science and Manufacturing. 2020. V. 131. Article 105783.
Полилов А.Н. Этюды по механике композитов. М.: ФизМатЛит. 2015. 320 с. ISBN 978-5-9221-1617-6.
Brooks H., Molony S. Design and manufactured parts with three dimensional continuous fibre reinforcement // Materials and Design. 2016. V. 90. P. 276.
Balla V.M., Kate K.H., Satyavolu J., Singh P., Ganesh J., Tadimeti D. Additive manufacturing of natural fiber reinforced polymer composites: Processing and prospects // Composites Part B: Engineering. 2019. V. 174. Article 106956.
Grüber B., Hufenbach W., Kroll L., Lepper M., Zhou B. Stress concentration analysis of fibre-reinforced multilayered composites with pin-loaded holes // Composites Science and Technology. 2007. V. 67. № 7. P. 1439.
Zeng Q.-D., Wang Z.-L., Ling L. A study of the influence of interfacial damage on stress concentrations in unidirectional composites // Composites Science and Technology. 1997. V. 57. № 1. P. 129.
Дударьков Ю.И., Левченко Е.А., Лимонин М.В. Расчетная оценка влияния краевых эффектов на свободной кромке отверстия на прочность слоистых композитов // Заводская лаборатория. Диагностика материалов. 2017. Т. 83. № 3. С. 59.
Akrami R., Fotouhi S., Fotouhi M., Bodaghi M., Bolouri A. High-performance bio-inspired composite T-joints// Composites Science and Technology. 2019. V. 184. Article 107840.
Малахов А.В., Полилов А.Н. Построение траекторий волокон, огибающих отверстие, и их сравнение со структурой древесины в зоне сучка // Проблемы машиностроения и надежности машин. 2013. № 4. С. 57.
Полилов А.Н., Арутюнова А.С., Татусь Н.А. Влияние концентрации напряжений вблизи захватов на реализацию прочности композитов при растяжении // Заводская лаборатория. Диагностика материалов. 2020. № 11. С. 35.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин