Проблемы машиностроения и надежности машин, 2020, № 5, стр. 56-65

Механизмы параллельной структуры с групповой кинематической развязкой, обеспечиваемой многопоточностью передачи энергии в кинематических цепях

К. Б. Саламандра^1, *, Л. И. Тывес¹, В. А. Глазунов¹, Е. С. Гебель²

¹ Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия

² Омский государственный технический университет
Омск, Россия

^* E-mail: ksalamandra@yandex.ru

Поступила в редакцию 25.03.2020
Принята к публикации 29.05.2020

DOI: 10.31857/S0235711920050120

Полный текст (PDF)

Аннотация

Манипуляционные механизмы параллельной структуры являются многопоточными системами, в которых параллельное размещение кинематических цепей позволяет увеличить нагрузочную способность, уменьшить размер и массу каждого из элементов, разгрузить подвижные звенья от силы тяжести приводов, разместив их на основании. В статье рассмотрен синтез нового механизма параллельной структуры с увеличенным числом параллельных потоков передачи энергии от приводов к выходному звену. Для созданного макета механизма, оснащенного приводами поступательного и вращательного перемещения выходного звена, определены рабочие зоны. Рассмотрен динамический анализ механизма параллельной структуры с тремя кинематическими цепями с учетом масс промежуточных звеньев.

Ключевые слова: многопоточная система, манипулятор, механизм параллельной структуры, синтез механизмов, рабочая зона

Манипуляционные робототехнические системы, использующие в своей основе механизмы параллельной структуры, являются одним из перспективных направлений развития машиностроения [1]. Механизмы параллельной структуры являются примером многопоточной системы. Именно многопоточность, как фундаментальное свойство механизмов данного типа, за счет распределения нагрузки по нескольким параллельным кинематическим цепям позволяет увеличить нагрузочную способность, уменьшить размеры и массу каждого из элементов, получить систему в виде жесткой пространственной фермы [2]. Кроме того, по сравнению с однопоточными манипуляторами с незамкнутыми кинематическими цепями последовательного соединения привода с выходным звеном повышается точность и скорость манипулирования, разгрузка подвижных звеньев манипулятора от силы тяжести приводов за счет их размещения на неподвижном основании [2, 3]. Дополнительным преимуществом манипуляционных механизмов параллельной структуры является однотипная архитектура каждой кинематической цепи, что упрощает технологию изготовления механизма [4].

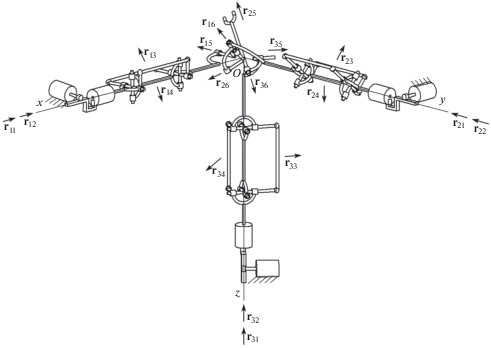
Примером многопоточной системы является механизм параллельной структуры, представленный на рис. 1, с шестью степенями свободы и тремя кинематическими цепями, в каждой из которых имеется карданный вал с двумя дополнительными связями и вращательными кинематическими парами, обеспечивающие угловые движения выходного звена. Кроме того, в каждой кинематической цепи имеет место два привода, расположенные соосно: линейный и вращательный. Основным достоинством механизма является полная групповая кинематическая развязка между положением и ориентацией выходного звена, т.е. кинематические связи между приводами ведущих звеньев, обеспечивающими поступательные перемещения выходного звена, и приводами, обеспечивающими его вращение, отсутствуют. Подобные механизмы исследовались в работах [5–12].

Рис. 1.

Кинематическая схема механизма с шестью степенями свободы и тремя кинематическими цепями.

Приводы манипулятора (рис. 1) расположены на основании, уменьшая таким образом инерционность подвижных звеньев, при этом возрастает удельная грузоподъемность механизма [2, 11].

Синтез механизма параллельной структуры с повышенной нагрузочной способностью. Принцип многопоточности, который присущ для рассматриваемого механизма (рис. 1) в целом, имеет место и в каждой кинематической цепи. Речь идет о карданном вале с двумя дополнительными связями, которые в данном случае обеспечивают постоянство взаимной ориентации осей двух шарниров Гука (“крестовин”). На рис. 1 показаны две дополнительные связи, каждая из которых крепится к шарниру Гука через сферические шарниры. Возможные движения обозначены векторами ${{{\mathbf{r}}}_{{11}}}$, ${{{\mathbf{r}}}_{{12}}}$, ${{{\mathbf{r}}}_{{13}}}$, ${{{\mathbf{r}}}_{{14}}}$, ${{{\mathbf{r}}}_{{15}}}$, ${{{\mathbf{r}}}_{{16}}}$, ${{{\mathbf{r}}}_{{21}}}$, ${{{\mathbf{r}}}_{{22}}}$, ${{{\mathbf{r}}}_{{23}}}$, ${{{\mathbf{r}}}_{{24}}}$, ${{{\mathbf{r}}}_{{25}}}$, ${{{\mathbf{r}}}_{{26}}}$, ${{{\mathbf{r}}}_{{31}}}$, ${{{\mathbf{r}}}_{{32}}}$, ${{{\mathbf{r}}}_{{33}}}$, ${{{\mathbf{r}}}_{{34}}}$, ${{{\mathbf{r}}}_{{35}}}$, ${{{\mathbf{r}}}_{{36}}}$. Более подробно представим первую кинематическую цепь. Вращательный и поступательные приводы определяют перемещения в направлении соответственно векторов ${{{\mathbf{r}}}_{{11}}}$ и ${{{\mathbf{r}}}_{{12}}}$. Векторы ${{{\mathbf{r}}}_{{13}}}$ и ${{{\mathbf{r}}}_{{14}}}$ соответствуют гипотетическим поступательным кинематическим парам, направления движения в которых перпендикулярны осям двух дополнительных связей, соответствующих имеющемуся в данной кинематической цепи карданному валу. Векторы ${{{\mathbf{r}}}_{{15}}}$ и ${{{\mathbf{r}}}_{{16}}}$ соответствуют двум вращательным кинематическим парам, при этом оси вращения пар всех кинематических цепей пересекаются в одной точке О.

Присутствующий в каждой кинематической цепи карданный вал с двумя дополнительными связями позволяет передать вращение с постоянным передаточным отношением, кроме того, он, в виду наличия дополнительных связей обеспечивает сохранение ориентации выходного звена при его поступательном перемещении.

Увеличение числа параллельных карданных валов в кинематических цепях позволяет повысить нагрузочную способность механизма. В случае, если число карданных шарниров будет равно двум, то это позволит передать вращение от входного вала к выходному, поскольку параллельно расположенные карданные валы и карданные шарниры будут работать согласовано. Однако в данном случае возможно и вращение плоскости второго карданного шарнира относительно плоскости первого карданного шарнира – это происходит вокруг оси, соединяющей центры и карданный шарнир (шарнир Гука). Для того, чтобы исключить вращение и обеспечить постоянство относительной ориентации плоскостей двух карданных шарниров необходимо наличие третьего карданного вала. При этом будет обеспечено постоянство передаточного отношения, равное единице, между входным и выходным валами этого “встроенного” карданного вала.

Таких параллельно расположенных карданных валов теоретически может быть любое количество, большее или равное трем.

На основе рассмотренной структуры кинематических цепей и механизма (рис. 1) синтезирован новый механизм с кинематической развязкой между поступательными и вращательными движениями выходного звена (рис. 2).

Рис. 2.

Механизм с кинематической развязкой между поступательными и вращательными движениями выходного звена с тремя карданными валами в каждой кинематической цепи.

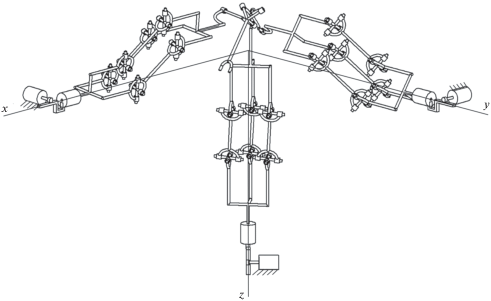
Отличие данного механизма заключается в том, что в каждой кинематической цепи имеется не один карданный вал, а три, расположенных параллельно. В исходном механизме (рис. 1) также имели место три стержня, один из которых соответствовал карданному валу, а два были дополнительными связями. При этом стержни имели разные функции, а в данном случае эти функции аналогичны.

Кинематический анализ макета механизма параллельной структуры с шестью степенями свободы и построение рабочих зон. В ИМАШ РАН в соответствии с кинематической схемой (рис. 1) был изготовлен макет механизма параллельной структуры, фотография которого представлена на рис. 3.

Рис. 3.

Макет механизма параллельной структуры с шестью степенями свободы и групповой кинематической развязкой движений.

Макет оснащен шестью приводами, закрепленными на неподвижном основании. Три поступательных привода выполнены в виде электродвигателя, зубчатого колеса и зубчатой рейки. Длины промежуточных звеньев равны 440 мм, допустимый ход зубчатой рейки 120 мм. Каждый из трех вращательных электроприводов также содержит на выходном валу зубчатое колесо, которое находится в зацеплении с круговым сектором. Угол сектора равен 180°, т.е. пределы изменения обобщенных координат механизма от –π/2 до π/2.

Конкретные параметры изготовленного образца механизма, обладающего линейными и вращательными двигателями, позволяют рассмотреть кинематические свойства изготовленного макета механизма параллельной структуры и построить рабочие зоны.

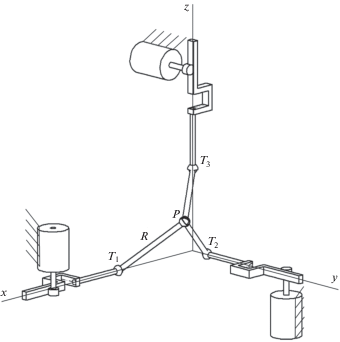
Полная групповая кинематическая развязка между положением и ориентацией выходного звена позволяет проводить кинематический анализ последовательно. На первом этапе рассмотрим поступательное перемещение выходного звена, при этом механизм можно представить в упрощенном виде (рис. 4), где расположенные ортогонально линейные двигатели связаны с рабочим органом посредством стержней.

Рис. 4.

Упрощенная кинематическая схема для анализа поступательного перемещения выходного звена.

Точки Ti и координаты Pi характеризуют положения зубчатых реек и выходного звена (i = 1, …, 3). При решении обратной задачи находим координаты Pi точки P, используя соотношения

${{\left( {{{x}_{P}} - {{x}_{{T1}}}} \right)}^{2}} + y_{P}^{2} + z_{P}^{2} - {{R}^{2}} = 0,$

(1)

$x_{P}^{2} + {{\left( {{{y}_{P}} - {{y}_{{T2}}}} \right)}^{2}} + z_{P}^{2} - {{R}^{2}} = 0,$

$x_{P}^{2} + y_{P}^{2} + {{\left( {{{z}_{P}} - {{z}_{{T3}}}} \right)}^{2}} - {{R}^{2}} = 0,$

где R – длины стержней.

Решение системы (1) осуществляется вычитанием из первого и второго уравнений третьего уравнения. Затем две полученные линейные зависимости между переменными подставляются в третье уравнение. Результатом подстановки является квадратное уравнение, решения которого

${{z}_{P}} = \frac{{ - B \pm \sqrt {{{B}^{2}} - 4AC} }}{{2A}},$

где $A = 4(z_{{T3}}^{2}y_{{T2}}^{2} + z_{{T3}}^{2}x_{{T1}}^{2} + x_{{T1}}^{2}y_{{T2}}^{2})$; $B = 4{{z}_{{T3}}}({{x}_{{T1}}}y_{{T2}}^{2} - z_{{T3}}^{2}y_{{T2}}^{2}$ + $x_{{T1}}^{2}{{y}_{{T2}}} - z_{{T3}}^{2}x_{{T1}}^{2} - 2x_{{T1}}^{2}y_{{T2}}^{2}$); $C = (x_{{T1}}^{2}$ + $y_{{T2}}^{2})(z_{{T3}}^{4}$ + $x_{{T1}}^{2}y_{{T2}}^{2})$ – $4{{R}^{2}}x_{{T1}}^{2}y_{{T2}}^{2}$.

Два решения соответствуют двум положениям точки P, однако из соображений технической реализуемости выбираем лишь одно положение. В результате получены следующие соотношения для решения прямой задачи о положениях выходного звена механизма параллельной структуры

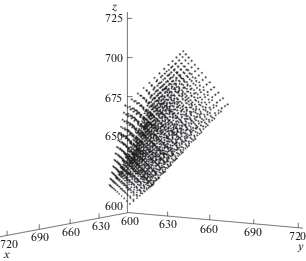
${{y}_{P}} = \frac{1}{{2{{y}_{{T2}}}}}\left( {y_{{T2}}^{2} + 2{{z}_{P}}{{z}_{{T3}}} - z_{{T3}}^{2}} \right),$

${{x}_{P}} = \frac{1}{{2{{x}_{{T1}}}}}\left( {x_{{T1}}^{2} + 2{{z}_{P}}{{z}_{{T3}}} - z_{{T3}}^{2}} \right).$

Подставляя допустимые значения обобщенных координат линейных двигателей x_T1, y_T2, z_T3, определяются значения координат x_p, y_p и z_p выходного звена. Таким образом для созданного макета (рис. 3) получена рабочая зона, представленная на рис. 5.

Рис. 5.

Рабочая зона поступательного перемещения выходного звена созданного макета.

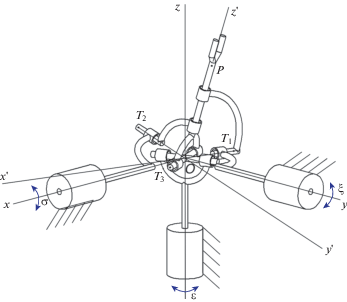
На втором этапе кинематического анализа рассмотрим сферическую часть механизма (рис. 6). Решим обратную задачу о положениях с помощью углов Эйлера.

Рис. 6.

Упрощенная кинематическая схема механизма вращения выходного звена.

Положение подвижной системы координат x', y', z', определяющее точку P выходного звена, задано углами Эйлера ψ, θ, φ (на рис. 6 не показаны). Тогда проекции точки P на оси неподвижной системы координат будут: ${{x}_{P}} = \sin \psi \sin \theta $; ${{y}_{P}} = - \cos {\psi }\sin {\theta }$; ${{z}_{P}} = \cos {\theta }$.

Проекции точки T₃ соответственно: ${{x}_{{{{T}_{3}}}}} = \cos \psi \cos \varphi $ – $\sin \psi \sin \varphi \cos \theta $; ${{y}_{{{{T}_{3}}}}}$ = = $\sin {\psi }\cos {\varphi }$ + $\cos {\psi }\sin {\varphi }\cos {\theta }$; ${{z}_{{{{T}_{3}}}}} = \sin {\varphi }\sin {\theta }$.

Повороты ведущих звеньев механизма (обобщенные координаты) определены углами σ, ξ, ε. При этом положительное направление – против часовой стрелки. Точки T₁ и T₂ и T₃ перемещаются по окружности единичного радиуса вокруг начала координат.

Поворот плоскости YOZ вокруг оси x на угол σ (рис. 6) позволяет записать соотношение

$\tan \sigma = \frac{{ - {{z}_{{T2}}}}}{{ - {{y}_{{T2}}}}} = \frac{{ - {{y}_{P}}}}{{{{z}_{P}}}} = \frac{{\cos \psi \sin \theta }}{{\cos \theta }} = \cos \psi \tan \theta .$

Аналогично, поворот плоскости XOZ вокруг оси y на угол ξ

$\tan \xi = \frac{{{{z}_{{T1}}}}}{{ - {{x}_{{T1}}}}} = \frac{{{{x}_{P}}}}{{{{z}_{P}}}} = \frac{{\sin \psi \sin \theta }}{{\cos \theta }} = \sin \psi \tan \theta .$

Поворот плоскости XOY вокруг оси z на угол ε

$\tan \varepsilon = \frac{{ - {{y}_{{T3}}}}}{{{{x}_{{T3}}}}} = \frac{{\sin \psi \cos \varphi + \cos \psi \sin \varphi \cos \theta }}{{\sin \psi \sin \varphi \cos \theta - \cos \psi \cos \varphi }}.$

Указанные решения обратной задачи о положениях выходного звена можно использовать для построения рабочей зоны с учетом предельных углов поворота во входных кинематических парах механизма параллельной структуры.

Задаем предельные эйлеровы углы ψ, θ, φ, заведомо большие чем те, которые возможны в данном механизме. В пределах изменения этих углов сканируем их с некоторым шагом, и всякий раз решаем задачу о положениях. Если соответствующие обобщенные координаты выходят за пределы допустимых значений, то данная точка отбрасывается. Если значения обобщенных координат находится в пределах допустимых значений, то точка запоминается.

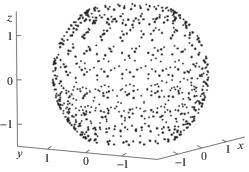
Вид рабочей зоны выходного звена сферического механизма в виде единичной окружности, полученный умножением единичного вектора ${\mathbf{OP}} = \left( {\begin{array}{*{20}{c}} 1 \\ 1 \\ 1 \end{array}} \right)$ на матрицу поворота

$\left( {\begin{array}{*{20}{c}} {\cos \psi \cos \varphi - \sin \psi \sin \varphi \cos \theta }&{\sin \psi \cos \varphi + \cos \psi \sin \varphi \cos \theta }&{\sin \varphi \sin \theta } \\ { - \cos \psi \sin \varphi - \sin \psi \cos \varphi \cos \theta }&{\cos \psi \cos \varphi \cos \theta - \sin \psi \sin \varphi }&{\cos \varphi \sin \theta } \\ {\sin \psi \sin \theta }&{ - \cos \psi \sin \theta }&{\cos \theta } \end{array}} \right)$

представлен на рис. 7.

Рис. 7.

Рабочая зона вращательного перемещения выходного звена созданного макета.

Динамический анализ механизма параллельной структуры. Исследованию динамики механизмов параллельной структуры посвящены, в частности, работы [13–15]. При этом для динамического анализа предполагается, что массы подвижных звеньев сосредоточены в одной точке – в выходном звене. Такое предположение существенно упрощает математические выкладки, но снижает точность и адекватность получаемых результатов. В настоящей статье динамический анализ механизма параллельной структуры проводится в предположении, что масса каждой из трех кинематических цепей равномерно распределена и сосредоточена в трех точках: на выходном звене, в геометрических центрах подвижных стержней и у приводов на неподвижном основании.

Исходя из изложенного, примем массу каждого стержня равной m. В соответствии с принципом возможных перемещений можно составить систему уравнений движения механизма. Ниже, в виду большого числа параметров, приведем уравнение только для проекции на ось x, вид двух оставшихся уравнений аналогичен.

$3\frac{m}{6}{{\ddot {x}}_{P}} + \frac{m}{6}{{\ddot {x}}_{{T1}}}\frac{{\partial {{x}_{{T1}}}}}{{\partial {{x}_{P}}}} + \frac{{2m}}{3}{{\ddot {x}}_{{C1}}}\frac{{\partial {{x}_{{C1}}}}}{{\partial {{x}_{P}}}} - {{F}_{1}}\frac{{\partial {{x}_{{T1}}}}}{{\partial {{x}_{P}}}} + \frac{m}{6}{{\ddot {y}}_{{T2}}}\frac{{\partial {{y}_{{T2}}}}}{{\partial {{x}_{P}}}} + \frac{{2m}}{3}{{\ddot {y}}_{{С2}}}\frac{{\partial {{y}_{{С2}}}}}{{\partial {{x}_{P}}}} + $

$ + \;\frac{{2m}}{3}{{\ddot {x}}_{{С2}}}\frac{{\partial {{x}_{{С2}}}}}{{\partial {{x}_{P}}}} - {{F}_{2}}\frac{{\partial {{y}_{{T2}}}}}{{\partial {{x}_{P}}}} + \frac{m}{6}{{\ddot {z}}_{{T3}}}\frac{{\partial {{z}_{{T3}}}}}{{\partial {{x}_{P}}}} + \frac{{2m}}{3}{{\ddot {z}}_{{С3}}}\frac{{\partial {{z}_{{С3}}}}}{{\partial {{x}_{P}}}} + \frac{{2m}}{3}{{\ddot {x}}_{{С3}}}\frac{{\partial {{x}_{{С3}}}}}{{\partial {{x}_{P}}}} - {{F}_{3}}\frac{{\partial {{z}_{{T3}}}}}{{\partial {{x}_{P}}}} = 0.$

Промежуточные звенья представляют собой три параллельно расположенных стержня, которые совершают аналогичные движения. Центр масс каждого стержня расположен в его центре, отсюда, зная координаты точек начала и конца стержня, определяем координаты центров масс C1, C2, C3 стержней

${{x}_{{C1}}} = {{x}_{P}} + \frac{{{{x}_{{T1}}} - {{x}_{P}}}}{2} = \frac{{{{x}_{P}} + {{x}_{{T1}}}}}{2},\quad {{y}_{{C1}}} = \frac{{{{y}_{P}}}}{2},\quad {{z}_{{C1}}} = \frac{{{{z}_{P}}}}{2},$

${{x}_{{C2}}} = \frac{{{{x}_{P}}}}{2},\quad {{y}_{{C2}}} = \frac{{{{y}_{P}} + {{y}_{{T2}}}}}{2},\quad {{z}_{{C2}}} = \frac{{{{z}_{P}}}}{2},$

${{x}_{{C3}}} = \frac{{{{x}_{P}}}}{2},\quad {{y}_{{C3}}} = \frac{{{{y}_{P}}}}{2},\quad {{z}_{{C3}}} = \frac{{{{z}_{P}} + {{z}_{{T3}}}}}{2}.$

Проекции скоростей и ускорений центров масс стрежней определяются дифференцированием координат по времени.

Частные производные (передаточные отношения) $\frac{{\partial {{y}_{{С2}}}}}{{\partial {{x}_{P}}}}$ = $\frac{{\partial {{z}_{{С3}}}}}{{\partial {{x}_{P}}}}$ = $\frac{{\partial {{x}_{{С1}}}}}{{\partial {{y}_{P}}}}$ = $\frac{{\partial {{z}_{{С3}}}}}{{\partial {{y}_{P}}}}$ = $\frac{{\partial {{x}_{{С1}}}}}{{\partial {{z}_{P}}}}$ = = $\frac{{\partial {{y}_{{С2}}}}}{{\partial {{z}_{P}}}}$ = 0, т.к. их функции не зависят от аргумента. Передаточные отношения $\frac{{\partial {{x}_{{T1}}}}}{{\partial {{x}_{P}}}}$, $\frac{{\partial {{y}_{{T2}}}}}{{\partial {{x}_{P}}}}$, $\frac{{\partial {{z}_{{T3}}}}}{{\partial {{x}_{P}}}}$, $\frac{{\partial {{x}_{{T1}}}}}{{\partial {{y}_{P}}}}$, $\frac{{\partial {{y}_{{T2}}}}}{{\partial {{y}_{P}}}}$, $\frac{{\partial {{z}_{{T3}}}}}{{\partial {{y}_{P}}}}$, скорости и ускорения приводов определяются дифференцированием системы уравнений (1) по обобщенным и абсолютным координатам. После алгебраических преобразований и тождественных подстановок система уравнений движения механизма может быть приведена к виду

$\frac{{5m}}{3}{{\ddot {x}}_{P}} + \frac{m}{6}\frac{{{{x}_{P}}}}{{{{y}_{P}} - {{y}_{{T2}}}}}{{\ddot {y}}_{P}} + \frac{m}{6}\frac{{{{x}_{P}}}}{{{{z}_{P}} - {{z}_{{T3}}}}}{{\ddot {z}}_{P}} = {{F}_{1}} + {{F}_{2}}\frac{{{{x}_{P}}}}{{{{y}_{P}} - {{y}_{{T2}}}}} + {{F}_{3}}\frac{{{{x}_{P}}}}{{{{z}_{P}} - {{z}_{{T3}}}}} - {{C}_{1}},$

$\frac{m}{6}\frac{{{{y}_{P}}}}{{{{x}_{P}} - {{x}_{{T1}}}}}{{\ddot {x}}_{P}} + \frac{{5m}}{3}{{\ddot {y}}_{P}} + \frac{m}{6}\frac{{{{y}_{P}}}}{{{{z}_{P}} - {{z}_{{T3}}}}}{{\ddot {z}}_{P}} = {{F}_{1}}\frac{{{{y}_{P}}}}{{{{x}_{P}} - {{x}_{{T1}}}}} + {{F}_{2}} + {{F}_{3}}\frac{{{{y}_{P}}}}{{{{z}_{P}} - {{z}_{{T3}}}}} - {{C}_{2}},$

$\frac{m}{6}\frac{{{{z}_{P}}}}{{{{x}_{P}} - {{x}_{{T1}}}}}{{\ddot {x}}_{P}} + \frac{m}{6}\frac{{{{z}_{P}}}}{{{{y}_{P}} - {{y}_{{T2}}}}}{{\ddot {y}}_{P}} + \frac{{5m}}{3}{{\ddot {z}}_{P}} = {{F}_{1}}\frac{{{{z}_{P}}}}{{{{x}_{P}} - {{x}_{{T1}}}}} + {{F}_{2}}\frac{{{{z}_{P}}}}{{{{y}_{P}} - {{y}_{{T2}}}}} + {{F}_{3}} - {{C}_{3}},$

где

${{C}_{1}} = \frac{m}{6}\left[ {3\left( {\frac{{2(\dot {x}_{P}^{2} + \dot {y}_{P}^{2} + \dot {z}_{P}^{2}) - {{y}_{P}}{{{\dot {y}}}_{P}} - {{z}_{P}}{{{\dot {z}}}_{P}}}}{{{{x}_{P}} - {{x}_{{T1}}}}} - 2{{{\dot {x}}}_{P}}} \right)} \right. + $

$ + \left( {\frac{{2(\dot {x}_{P}^{2} + \dot {y}_{P}^{2} + \dot {z}_{P}^{2}) - {{x}_{P}}{{{\dot {x}}}_{P}} - {{z}_{P}}{{{\dot {z}}}_{P}}}}{{{{y}_{P}} - {{y}_{{T2}}}}} - 2{{{\dot {y}}}_{P}}} \right)\frac{{{{x}_{P}}}}{{{{y}_{P}} - {{y}_{{T2}}}}} + $

$ + \left. {\left( {\frac{{2(\dot {x}_{P}^{2} + \dot {y}_{P}^{2} + \dot {z}_{P}^{2}) - {{x}_{P}}{{{\dot {x}}}_{P}} - {{y}_{P}}{{{\dot {y}}}_{P}}}}{{{{z}_{P}} - {{z}_{{T3}}}}} - 2{{{\dot {z}}}_{P}}} \right)\frac{{{{x}_{P}}}}{{{{z}_{P}} - {{z}_{{T3}}}}}} \right];$

C₂, C₃ – выражения, аналогичные C₁.

Таким образом, получена система уравнений для определения сил, действующих в приводах по заданным скоростям и ускорениям выходного звена, которую можно решить с помощью правила Крамера.

При численном моделировании движения данного механизма принимаем следующий подход к управлению этим объектом. Зная положения и скорости в каждой из кинематических цепей, определяем положения и скорости на выходном звене. Сравниваем реальные положения и скорости с требуемыми и умножаем на соответствующие коэффициенты. Реальные ускорения принимаем равными сумме упомянутых невязок, умноженных на указанные коэффициенты.

${{\ddot {x}}_{P}} = {{k}_{1}}\left( {{{{\dot {x}}}_{{P{\text{зад}}}}} - {{{\dot {x}}}_{P}}} \right) + {{k}_{2}}\left( {{{x}_{{P{\text{зад}}}}} - {{x}_{P}}} \right),$

${{\ddot {y}}_{P}} = {{k}_{1}}\left( {{{{\dot {y}}}_{{P~{\text{зад}}}}} - {{{\dot {y}}}_{P}}} \right) + {{k}_{2}}\left( {{{y}_{{P{\text{зад}}}}} - {{y}_{P}}} \right),$

${{\ddot {z}}_{P}} = {{k}_{1}}\left( {{{{\dot {z}}}_{{P{\text{зад}}}}} - {{{\dot {z}}}_{P}}} \right) + {{k}_{2}}\left( {{{z}_{{P{\text{зад}}}}} - {{z}_{P}}} \right).$

Здесь ${{x}_{{P{\text{зад}}}}}$, ${{y}_{{P{\text{зад}}}}}$, ${{z}_{{P{\text{зад}}}}}$, ${{\dot {x}}_{{P{\text{зад}}}}}$, ${{\dot {y}}_{{P{\text{зад}}}}}$, ${{\dot {z}}_{{P{\text{зад}}}}}$ – заданные координаты и скорости, изменяющиеся во времени; x_p, y_p, z_p, ${{\dot {x}}_{P}}$, ${{\dot {y}}_{P}}$, ${{\dot {z}}_{P}}$ – реальные положения и скорости.

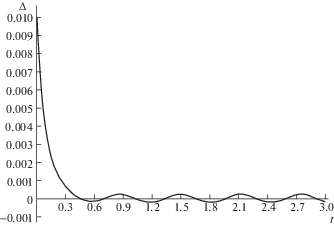
При численном эксперименте были заданы параметры: масса каждого стержня m = = 0.9 кг, длина стержня R = 0.4 м. Для примера приведем результат численного эксперимента, когда требуемый закон изменения координат: ${{x}_{{P{\text{зад}}}}} = 0.1 + 0.01\sin \omega t$; ${{y}_{{P{\text{зад}}}}} = 0.1 + 0.01\sin \omega t$; ${{z}_{{P{\text{зад}}}}} = 0.1 + 0.01\sin {\omega }t$; ${\omega } = 10$ рад/сек; ${{k}_{1}} = 720.2$; ${{k}_{2}} = 7.202 \times {{10}^{3}}$. Начальные условия были равны ${{x}_{{P~0}}} = 0.11$; ${{\dot {x}}_{{P~0}}} = 0$; ${{y}_{{P~0}}} = 0.1$; ${{\dot {y}}_{{P~0}}} = 0$; ${{z}_{{P~0}}} = 0.1$; ${{\dot {z}}_{{P~0}}} = 0$.

В результате решения дифференциальных уравнений получен график изменения ошибки положения по координате x_p (рис. 8).

Рис. 8.

График изменения ошибки по координате x_p выходного звена.

Результаты. Принцип многопоточности является основой построения механизмов параллельной структуры, имеющих несколько кинематических цепей и воспринимающих нагрузку подобно неподвижным пространственным фермам. Такая архитектура позволяет повысить нагрузочную способность и скорость движения звеньев, поскольку все приводы можно разместить на основании, а выходное звено совершает различное движение с несколькими степенями свободы. Однако этот же принцип, примененный в отношении одной из кинематических цепей, позволяет достичь, в частности, кинематической развязки, отделив поступательные движения от вращательных. В рассмотренном случае имеет место шесть “потоков”, которые разделены на две группы.

Для созданного макета механизма параллельной структуры с шестью степенями свободы, оснащенного тремя поступательными и тремя вращательными приводами, были построены рабочие зоны.

Решена, ранее не рассмотренная, задача анализа динамических свойств механизма параллельной структуры в предположении, что масса механизма равномерно распределена вдоль подвижных кинематических цепей механизма и сосредоточена в трех точках: на выходном звене, в геометрических центрах подвижных стержней и у приводов на неподвижном основании. Проведено численное моделирование движения механизма по заданному закону управления.

Список литературы

Ганиев Р.Ф. О современном состоянии и перспективах развития ИМАШ РАН. Проблемы механики машин и прорывных технологий // Проблемы машиностроения и надежности машин. 2014. № 3. С. 11.
Крайнев А.Ф. Идеология конструирования. М.: Машиностроение-1. 2003. 384 с.
Велиев Е.И., Ганиев Р.Ф., Глазунов В.А., Филиппов Г.С., Терехова А.Н. Разработка и решение задачи о положениях механизма параллельно-последовательной структуры для хирургических операций как альтернатива роботу Da Vinci // Проблемы машиностроения и надежности машин. 2019. № 4. С. 3.
Ганиев Р.Ф., Глазунов В.А. Манипуляционные механизмы параллельной структуры и их приложения в современной технике // Доклады академии наук. 2014. Т. 459. № 4. С. 428.
Gosselin C.M., Angeles J. Singularity Analysis of Closed Loop Kinematic Chains // IEEE Trans. on Robotics and Automation. 1990. № 6(3). P. 281.
Merlet J.P. Parallel Robots // Kluwer Academic Publishers. 2000. 372 p.
Chablat D., Wenger P. Architecture optimization of a 3-DOF translational parallel mechanism for machining applications, the orthoglide // IEEE Transactions on Robotics and Automation. 2003. V. 19. № 3. P. 403.
Kong X., Gosselin C. Type Synthesis of Parallel Mechanisms // Springer-Verlag Berlin Heidelberg. 2007. 272 p.
Данилин П.О., Тывес Л.И., Глазунов В.А. Групповая кинематическая развязка двигателей в механизмах параллельной структуры // Проблемы машиностроения и надежности машин, 2010. № 3. С. 27.
Хейло С. Решение задачи кинематики сферического манипулятора параллельной структуры // Машиностроение и инженерное образование. 2010. С. 18.
Glazunov V., Nosova N., Kheylo S., Tsarkov A. Design and Analysis of the 6-DOF Decoupled Parallel Kinematics Mechanism // Dynamic Decoupling of Robot Manipulators. Mechanisms and Machine Science. 2018. V. 56. Springer, Cham.
Nayak A., Caro S., Wenger P. Operation modes and workspace of a 4-rRUU Parallel Manipulator // IFToMM World Congress Proc. Mechanisms and Machine Science, 2019. V. 73. P. 649.
Mianowski K. Dynamically Decoupled Parallel Manipulator With Six Degrees of Freedom for Fast Assembly // Proc. Int. Conf. ISOM'2002. Chemnitz, 2002. P. 274.
Жога В.В., Герасун В.М., Несмиянов И.А., Воробьева Н.С., Дяшкин-Титов В.В. Динамический синтез оптимальных программных движений манипулятора-трипода // Проблемы машиностроения и надежности машин. 2015. № 2. С. 85.
Abo-Shanab R.F. Dynamic modeling of parallel manipulators based on Lagrange–D’Alembert formulation and Jacobian/Hessian matrices // Multibody Syst. Dyn. 2019.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал