Проблемы машиностроения и надежности машин, 2020, № 5, стр. 75-86
Метод поиска субоптимального воздействия, обеспечивающего допустимые потери в качестве технологического процесса
Д. С. Соловьев 1, *, И. А. Соловьева 2, Ю. В. Литовка 2, В. А. Нестеров 3
1 Тамбовский государственный университет имени Г.Р. Державина
Тамбов, Россия
2 Тамбовский государственный технический университет
Тамбов, Россия
3 Московский авиационный институт (национальный исследовательский университет)
Москва, Россия
* E-mail: solovjevdenis@mail.ru
Поступила в редакцию 17.03.2020
Принята к публикации 29.05.2020
Аннотация
Применение найденного управления для многомерных объектов может быть неоптимальным в условиях неопределенности значений входных координат и повлечь за собой недопустимые потери качества технологического процесса. Для решения проблемы предлагается метод поиска субоптимального управления, заключающийся в построении матрицы управления из значений входных координат, управляющих воздействий и критериев управления, расстояние между соседними значениями которых обеспечивает допустимые потери качества процесса. Для снижения объема просматриваемых элементов в матрице на этапе проектирования системы предлагается осуществить их предварительную кластеризацию. На этапе эксплуатации для измеренных значений входных координат осуществляется поиск кластера с ближайшим центром, среди элементов которого по наименьшему расстоянию выбирается вектор из матрицы управления. На примере гальванического хромирования шеек коленчатых валов показана эффективность разработанного метода.
Технический прогресс в машиностроении достигается за счет совершенствования конструкций машин и механизмов, а также производственных процессов их изготовления. Решению проблем совершенствования конструкций различных машин и механизмов посвящены работы [1–7]. Решению проблем совершенствования производственных процессов, направленных на повышение качества получаемой конструкции машины или механизма посредством поиска и реализации оптимального воздействия (управления) для различных технологических процессов их изготовления, посвящены работы [8–13]. Поиск оптимального управления технологическим процессом осуществляется по двум стратегиям. Согласно первой стратегии оптимальное управление находится в режиме реального времени (метод динамического программирования, принцип максимума Понтрягина) – во время протекания технологического процесса при изменении вектора входных координат определяется соответствующая экстремаль. К недостаткам метода динамического программирования, применяемого при решении задач такого класса, относятся значительный объем неиспользуемых вычислений, а также трудность подхода к многомерным объектам управления, поскольку при большой размерности задачи ее решение ограничивается памятью и быстродействием используемых вычислительных устройств [14–16]. Недостатком принципа максимума Понтрягина является невозможность его использования в задачах, для которых отсутствуют выпуклые свойства гамильтониана [17–19]. Согласно второй стратегии для заданных значений вектора входных координат осуществляется предварительный поиск оптимального управления с использованием адекватных математических моделей технологического процесса. Данная стратегия особенно часто применяется при управлении объектами, которые описываются дифференциальными уравнениями в частных производных [20–22], ввиду невозможности решения задач такого типа в режиме реального времени. В свою очередь, последующая реализация полученных результатов на объекте управления затрудняется неопределенностью, обусловленной произвольными значениями вектора входных координат. Применение найденного в последнем случае управления уже не будет оптимальным и может повлечь за собой недопустимые потери качества протекания технологического процесса. Назовем такое управление “субоптимальным”. Поэтому актуальной задачей является разработка эффективного с точки зрения вычислительной сложности метода поиска субоптимального управления для произвольных значений вектора входных координат, использование которого обеспечит допустимые потери качества технологического процесса.
Материалы и методы. Пусть изменение поведения объекта управления на временном интервале $T = \left\{ {\tau {\kern 1pt} :\;{{\tau }_{0}} \leqslant \tau \leqslant {{\tau }_{1}}} \right\}$ описывается системой уравнений
(2)
$x = {{\left( {{{x}_{1}}\left( \tau \right),{{x}_{2}}\left( \tau \right),...,{{x}_{n}}\left( \tau \right),...,{{x}_{N}}\left( \tau \right)} \right)}^{T}},$(3)
$y = {{\left( {{{y}_{1}}\left( \tau \right),{{y}_{2}}\left( \tau \right),...,{{y}_{{v}}}\left( \tau \right),...,{{y}_{V}}\left( \tau \right)} \right)}^{T}},$(4)
$u = {{\left( {{{u}_{1}}\left( \tau \right),{{u}_{2}}\left( \tau \right),...,{{u}_{m}}\left( \tau \right),...,{{u}_{M}}\left( \tau \right)} \right)}^{T}},$Тогда постановка всевозможных K задач поиска оптимальных управлений вида
для неизвестных начальных условий (1) бессмысленна ввиду бесконечного множества найденных экстремалей (4), хранение которых в вычислительном устройстве системы управления не представляется возможным.Сведем бесконечное множество значений входных координат (2) к конечному числу
где L – количество значений; $X$ – область изменения (2).Для выбранных значений (6) L раз решим K задач поиска оптимального управления (5). Из полученных результатов (5), (6) сформируем матрицу управления ${{{\Psi }}_{{LH}}}$ размерностью L строк и H = (N + 2K) столбцов, каждая строка в которой имеет вид
где $u_{l}^{*}$ – набор векторов оптимальных управляющих воздействий, размерностью K компонентов $J_{l}^{*}[{{y}_{l}},u_{l}^{*}]$ – набор векторов оптимальных значений критериев управления, размерностью K компонентовСформированная матрица ${{{\Psi }}_{{LH}}}$ сохраняется в вычислительном устройстве системы управления. Для вектора измеренных значений входных координат ${{x}^{{measured}}}$ на объекте управления отыскивается l-я строка в ${{{\Psi }}_{{LH}}}$, для которой выполняется равенство
Если l-я строка существует, то на исполнительное устройство системы управления подается k-е управление $u_{{lk}}^{*}$ согласно выбранному критерию управления $J_{{lk}}^{*}[{{y}_{{lk}}},u_{{lk}}^{*}]$.
Ввиду ограниченности размерности в строках матрицы управления условие (8), в общем случае, не будет выполняться для произвольного вектора входных координат объекта управления. В таком случае предлагается воспользоваться предположением: чем ближе между собой два вектора входных координат объекта управления, тем ближе между собой их наборы векторов оптимальных управляющих воздействий и критериев управления выходными координатами. Формализуем данное предположение если $||{\kern 1pt} {{x}_{l}} - {{x}^{{measured}}}{\kern 1pt} ||$ → 0, то $||{\kern 1pt} u_{l}^{*} - u_{{{{x}^{{measured}}}}}^{*}{\kern 1pt} ||$ → 0 и $||{\kern 1pt} J_{l}^{*}[{{y}_{l}},u_{l}^{*}]$ – $J_{{{{x}^{{measured}}}}}^{*}[{{y}^{{measured}}}$, $u_{{{{x}^{{measured}}}}}^{*}]\,||$ → 0, где $u_{{{{x}^{{measured}}}}}^{*}$, $J_{{{{x}^{{measured}}}}}^{*}[{{y}^{{measured}}}$, $u_{{{{x}^{{{\text{measured}}}}}}}^{*}]$ – набор векторов оптимальных управляющих воздействий и значений критериев управления для ${{x}^{{measured}}}$; ${{y}^{{measured}}}$ – вектор измеренных значений выходных координат.
Соответствующие потери в качестве протекания процесса на объекте управления определяются по формуле
Тогда задачу поиска субоптимального управления с использованием матрицы ${{{\Psi }}_{{LH}}}$ можно сформулировать следующим образом: найти для измеренного ${{x}^{{measured}}}$ на объекте управления такое ${{x}_{l}}$, которое обеспечивает
(9)
$l{\kern 1pt} * = \mathop {\arg \min }\limits_{l = 1,2,...,L} {{{\rho }}_{l}}({{x}_{l}},{{x}^{{measured}}})$(10)
${\delta }J_{{{{x}^{{measured}}}}}^{*}[{{y}^{{measured}}},u_{{l*}}^{*}] \leqslant {\delta }{{J}^{s}} = ({\delta }J_{1}^{s},{\delta }J_{2}^{s},...,{\delta }J_{K}^{s}),$С одной стороны, матрица ${{{\Psi }}_{{LH}}}$ должна содержать большое количество строк для обеспечения требуемой точности управления. С другой стороны, ее размерность должна быть минимальной, что обосновывается, прежде всего, тем, что L раз решение K задач поиска оптимального управления (5) может быть связано со значительным объемом времени. Последнее обстоятельство для произвольного выбора L в (6) не гарантирует наличие в матрице управления строки $l{\kern 1pt} *$ с компонентом $u_{{l*}}^{*}$, для которой выполняется ограничение (10).
Сформулируем задачу построения матрицы управления. Пусть требуется найти наименьшую размерность L матрицы ${{{\Psi }}_{{LH}}}$, а также соответствующие ей значения (7) такие, что $\forall {{x}^{{measured}}}$ использование найденного $u_{{l*}}^{*}$ обеспечит выполнение ограничения (10).
Для решения сформулированной задачи необходимо выполнить следующую последовательность действий:
1) построить таблицу W оптимальных значений критериев (5) с регулярным, достаточно большим шагом в координатах (6);
2) аппроксимировать каждый рассчитанный оптимальный критерий (5) сильно выпуклой (например, квадратичной) аналитической зависимостью [23–25]
(11)
$J_{k}^{a}\left( x \right) = {{c}_{0}} + \sum\limits_{n = 1}^N {{{c}_{{1n}}}} {{x}_{n}}\left( {\tau } \right) + \sum\limits_{n = 1}^N {{{c}_{{2n}}}} x_{n}^{2}\left( {\tau } \right) + \prod\limits_{n = 1}^N {{{c}_{{3n}}}{{x}_{n}}\left( {\tau } \right)} ,$3) определить изолинии для каждой зависимости (11) с соответствующим шагом ${\delta }J_{{}}^{s}$ и отыскать значение ${{x}_{l}}$ при перемещении вдоль каждой из изолиний.
Выполнение описанных действий позволит наполнить матрицу управления такими ${{x}_{1}},{{x}_{2}},...,{{x}_{l}}$, ${{x}_{{l + 1}}},...,{{x}_{L}}$, расстояние между соседними значениями которых ${\rho }\left( {{{x}_{l}},{{x}_{{l + 1}}}} \right)$ обеспечивает выполнение ограничения (10). В связи с чем ограничение (10) будет также выполняться и $\forall {{x}^{{measured}}}$, находящегося на минимальном расстоянии от ${{x}_{{{{l}^{*}}}}}$.
Таким образом, сформулированная задача условной минимизации (9) с ограничением (10) сведется к задаче безусловной минимизации.
Поиск подходящей l*-й строки в построенной матрице ${{{\Psi }}_{{LH}}}$ методом полного перебора приведет к снижению эффективности работы системы управления, поэтому рассмотрим эффективный по вычислительной сложности метод поиска субоптимального управления.
Пусть для вектора $x_{{}}^{{measured}}$ определено 2N границ изменения значений каждого компонента
(12)
$\left\{ \begin{gathered} x_{1}^{{\min }} = \min \left( {{{x}_{1}}\left( {\tau } \right)} \right) \leqslant x_{1}^{{measured}}\left( {\tau } \right) \leqslant x_{1}^{{\max }} = \max \left( {{{x}_{1}}\left( {\tau } \right)} \right), \hfill \\ ... \hfill \\ x_{n}^{{\min }} = \min \left( {{{x}_{n}}\left( {\tau } \right)} \right) \leqslant x_{n}^{{measured}}\left( {\tau } \right) \leqslant x_{n}^{{\max }} = \max \left( {{{x}_{n}}\left( {\tau } \right)} \right), \hfill \\ ... \hfill \\ x_{N}^{{\min }} = \min \left( {{{x}_{N}}\left( {\tau } \right)} \right) \leqslant x_{N}^{{measured}}\left( {\tau } \right) \leqslant x_{N}^{{\max }} = \max \left( {{{x}_{N}}\left( {\tau } \right)} \right), \hfill \\ \end{gathered} \right.$Для облегчения поиска информации в матрице управления введем нормализованный вектор ${{\bar {x}}_{l}}$, соответствующий вектору ${{x}_{l}}$, компоненты которого рассчитываются согласно (12) как
(13)
${{\bar {x}}_{l}} = \left( {{{{\bar {x}}}_{{l1}}} = \frac{{\left| {{{x}_{{l1}}}\left( {\tau } \right) - x_{1}^{{\min }}} \right|}}{{\left| {x_{1}^{{\max }} - x_{1}^{{\min }}} \right|}},...,{{{\bar {x}}}_{{ln}}} = \frac{{\left| {{{x}_{{ln}}}\left( {\tau } \right) - x_{n}^{{\min }}} \right|}}{{\left| {x_{n}^{{\max }} - x_{n}^{{\min }}} \right|}},...,{{{\bar {x}}}_{{lN}}} = \frac{{\left| {{{x}_{{lN}}}\left( {\tau } \right) - x_{N}^{{\min }}} \right|}}{{\left| {x_{N}^{{\max }} - x_{N}^{{\min }}} \right|}}} \right).$Нормализуя компоненты измеренного вектора ${{x}^{{measured}}}$, используя формулы, аналогичные (13), получим вектор ${{\bar {x}}^{{measured}}}$. Значения компонентов нормализованных векторов ${{\bar {x}}_{l}}$ и ${{\bar {x}}^{{measured}}}$ находятся в диапазоне [0; 1].
Тогда расстояние ρl в (9) для ${{\bar {x}}_{l}}$ и ${{\bar {x}}^{{measured}}}$ можно формализовать согласно различным метрикам с использованием весовых коэффициентов ${{\nu }_{1}},...,{{\nu }_{n}},...,{{\nu }_{N}}$, определяющих важность каждой компоненты с точки зрения ее влияния на соответствующий критерий управления
Для уменьшения объема просматриваемых вариантов подходящих ${{\bar {x}}_{l}}$ в ${{{\Psi }}_{{LH}}}$ предлагается следующая последовательность действий:
1) разбить ${{\bar {x}}_{l}}$ в ${{{\Psi }}_{{LH}}}$ на Q кластеров согласно выбранному методу кластеризации A – $A{\kern 1pt} :\;{{\bar {x}}_{l}} \to q$, с нахождением центров ${{\bar {x}}_{q}}$ (q = 1, 2, …, Q) $\sum\nolimits_{{{p}_{q}}} {\rho \left( {{{{\bar {x}}}_{l}},{{{\bar {x}}}_{q}}} \right)} $ → min, где ${{p}_{q}}$ – количество элементов, содержащихся в q кластере;
2) определить среди всех кластеров Q такой кластер q*, для которого расстояние между его центром и ${{\bar {x}}^{{measured}}}$ минимально
(14)
$q{\kern 1pt} * = \mathop {\arg \min }\limits_{q = 1,2,...,Q} {{{\rho }}_{q}}({{\bar {x}}_{q}},{{\bar {x}}^{{measured}}}),$3) отыскать решение задачи (9) среди всех ${{\bar {x}}_{l}}$, которые входят в q*-й кластер
(15)
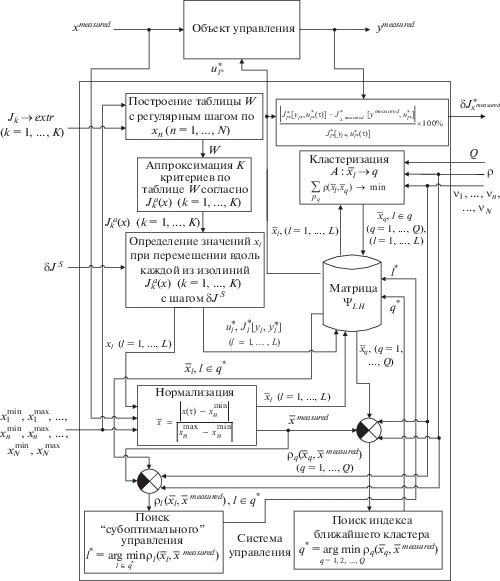
$l{\kern 1pt} * = \mathop {\arg \min }\limits_{l \in q*} {{{\rho }}_{l}}({{\bar {x}}_{l}},{{\bar {x}}^{{measured}}}).$На рис. 1 приводится структурная схема системы субоптимального управления.
Задачи наполнения матрицы ${{{\Psi }}_{{LH}}}$ значениями ${{x}_{1}}$, ${{x}_{2}}$, …, ${{x}_{l}}$, ${{x}_{{l + 1}}}$, …, ${{x}_{L}}$, расстояние ${\rho }\left( {{{x}_{l}},{{x}_{{l + 1}}}} \right)$ между которыми обеспечивает допустимые потери качества протекания процесса, их последующей нормализации и кластеризации решаются только один раз при проектировании системы субоптимального управления. А решение задач поиска кластера q*, отыскания в нем ${{\bar {x}}_{{l*}}}$, ближайшего к ${{\bar {x}}^{{measured}}}$, с соответствующим ему $u_{{l*}}^{*}$ и последующей оценкой ${\delta }J_{{{{x}^{{measured}}}}}^{*}$ позволяет значительно уменьшить количество просматриваемых значений в ${{{\Psi }}_{{LH}}}$ и осуществляется в процессе эксплуатации системы субоптимального управления.
Экспериментальная часть. Для увеличения износостойкости шеек коленчатых валов применяют гальваническое хромирование их поверхности [26]. Рассмотрим построение системы субоптимального управления гальваническим процессом хромирования коленчатых валов.
Вектор входных координат х содержит количество компонентов N = 3, в качестве которых выступают: 1) ${{x}_{1}}\left( {\tau } \right) = {{S}_{{\text{c}}}}$ – площадь поверхности шеек коленчатого вала, дм2; 2) ${{x}_{2}}\left( {\tau } \right) = {{L}_{{{\text{el}}}}}$ – уровень электролита в ванне, дм; 3) ${{x}_{3}}\left( {\tau } \right) = {{C}_{{{\text{Cr}}{{{\text{O}}}_{{\text{3}}}}}}}$ – концентрация хромового ангидрида в электролите, г/л.
Изменение площади поверхности покрываемой детали (коленчатого вала) обуславливается количеством шатунных шеек, определяемых в зависимости от числа цилиндров, и происходит согласно функции Хевисайда только в начальный момент времени и остается постоянной в течение процесса. Изменение уровня электролита и концентрации хромового ангидрида происходит не только из-за испарения растворителя (воды) и потребления компонентов при электрохимических и химических реакциях во время протекания процесса, но и за счет выноса электролита на поверхностях обработанных деталей и его разбавления водой, находящейся на поверхности поступающих на обработку деталей.
Определение $\bar {x}_{1}^{{measured}}$ осуществляется путем ее деления на элементарные плоскости и фигуры, площади которых рассчитываются отдельно, а затем суммируются, или с использованием встроенного механизма расчета площади детали по ее чертежу при использовании компьютерных систем трехмерного моделирования. Определение $x_{2}^{{measured}}$ осуществляется с использованием погружного датчика. Определение $x_{3}^{{measured}}$ осуществляется с использованием ареометра, термометра и таблицы концентрации хромового ангидрида.
Для изменения каждого компонента вектора х определено 2N границ
1) $x_{1}^{{\min }} = 12.5 \leqslant {{x}_{1}}\left( {\tau } \right) \leqslant x_{1}^{{\max }} = 21.5$ дм2; 2) $x_{2}^{{\min }} = 4 \leqslant {{x}_{2}}\left( \tau \right) \leqslant x_{2}^{{\max }}$ = 5 дм; 3) $x_{3}^{{\min }}$ = = 200 ≤ ${{x}_{3}}\left( {\tau } \right)$ ≤ $x_{3}^{{\max }}$ = 250 г/л.
Износостойкость гальванического хромового покрытия определяется его толщиной. Вектор выходных координат $y$ содержит количество компонентов V = 1, в качестве которого выступает ${{y}_{1}}\left( {\tau } \right) = \delta \left( {{{x}_{{{{S}_{c}}}}},{{y}_{{{{S}_{c}}}}},{{z}_{{{{S}_{c}}}}},{\tau }} \right)$ – толщина хромового покрытия в точке с координатами $\left( {{{x}_{{{{S}_{c}}}}},{{y}_{{{{S}_{c}}}}},{{z}_{{{{S}_{c}}}}}} \right)$ на поверхности детали в момент τ, мкм.
Определение $y_{{\text{1}}}^{{measured}}$ осуществляется с использованием электромагнитного толщиномера покрытий согласно [27].
Оценка распределения толщины гальванического покрытия на поверхности детали осуществляется согласно критерию равномерности.
Постановка K = 1 задачи поиска оптимального управления имеет вид
В качестве управляющих воздействий выбирается реверсирование тока, механизм воздействия на равномерность покрытия заключается в том, что: 1) при обратном (отрицательном) импульсе идет анодное стравливание металла на больших градиентах тока, т.е. именно там, где произошло большое наращивание при прямом токе; 2) интенсифицируется разрушение концентрационной катодной поляризации, что способствует обновлению раствора в прикатодном слое.
Вектор управляющих воздействий и содержит количество компонентов M = 4, в качестве которых выступают: 1) ${{u}_{1}}\left( {\tau } \right) = {{I}_{с}}$ – сила тока для катодного полупериода, А; 2) ${{u}_{2}}\left( {\tau } \right) = {{\tau }_{с}}$ – длительность катодного полупериода, с; 3) ${{u}_{3}}\left( {\tau } \right) = {{I}_{a}}$ – сила тока для анодного полупериода, А; 4) ${{u}_{4}}\left( {\tau } \right) = {{\tau }_{a}}$ – длительность анодного полупериода, с.
В работе [28] для решения задачи оптимального управления гальваническим процессом с реверсом тока описывается математическая модель, базирующаяся на уравнениях теоретической электрохимии и математической физики, которая связывает критерий равномерности покрытия и выбранные управляющие воздействия.
Допустимые потери в качестве управления ${\delta }J_{1}^{s}$ = 10%.
Кластеризация осуществляется по методу k-means [29] с использованием расстояния Евклида ${{\rho }_{l}}({{\bar {x}}_{l}},{{\bar {x}}^{{measured}}})$ = $\sqrt {\sum\nolimits_{n = 1}^N {{{\nu }_{n}}{{{({{{\bar {x}}}_{{ln}}} - \bar {x}_{n}^{{measured}})}}^{2}}} } $.
Весовые коэффициенты имеют значения: ${{{\nu }}_{1}}$ = 0.65; ${{{\nu }}_{2}}$ = 0.25; ${{{\nu }}_{3}}$ = 0.1.
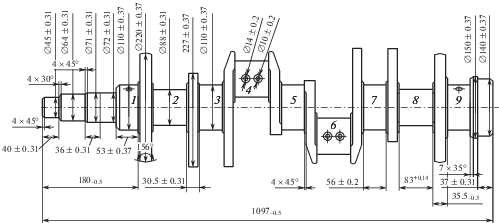
Компоненты вектора $\bar {x}_{{}}^{{measured}}$ = (0.2775; 0.2395; 0.637) соответствуют коленчатому валу ЯМЗ-238, чертеж которого представлен на рис. 2, с суммарной площадью 15 дм2 поверхности шеек 1–9, обрабатываемому в ванне с уровнем электролита 4.23 дм, имеющим концентрацию хромового ангидрида 232 г/л.
Результаты и их обсуждение. При построении матрицы ${{{\Psi }}_{{LH}}}$ для нее найдены наименьшая размерность L = 1331 и элементы ${{x}_{1}},{{x}_{2}},...,{{x}_{l}},...,{{x}_{L}}$, которые обеспечивают $\forall {{x}^{{measured}}}$ выполнение ограничения на потери качества протекания гальванического процесса не более $\delta J_{1}^{s}$.
Известно, что вычислительная сложность алгоритма кластеризации по методу k‑means составляет O(N Q it L) и имеет линейное время.
На рис. 3 представлены зависимости итераций it и объема N Q it L входных данных, определяющие вычислительную сложность алгоритма k-means, при изменении количества кластеров 2 ≤ Q ≤ 200 ед. для кластеризации найденных элементов матрицы управления.
Рис. 3.
Зависимости итераций it (а) и объема N Q it L входных данных (б), определяющие вычислительную сложность алгоритма k-means для кластеризации элементов матрицы управления.
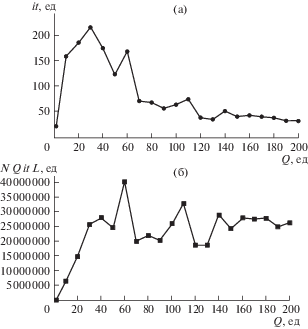
Максимальное значение вычислительной сложности алгоритма k-means для сформированной матрицы управления достигается при количестве кластеров Q = 60 и соответствующем ему объеме входных данных N Q it L = 4 048 902 ед.
Поскольку кластеризация выполняется только один раз при проектировании системы, то эффективность в плане быстродействия поиска субоптимального управления в процессе ее (системы) эксплуатации будет полностью обуславливаться вычислительной сложностью алгоритма решения задач (14)–(15), которая определяется согласно O(N[Q + ${{p}_{{q*}}}$]). Здесь ${{p}_{{q*}}}$ является максимальным значением из ${{p}_{q}}$.
На рис. 4 представлены зависимости $N{{p}_{{q*}}}$ максимального количества элементов и соответствующего объема N[Q + ${{p}_{{q*}}}$] входных данных, определяющие вычислительную сложность алгоритма поиска субоптимального управления в процессе эксплуатации системы, при изменении количества кластеров 2 ≤ Q ≤ 200 ед. при проектировании системы.
Рис. 4.
Зависимости $N{{p}_{{q*}}}$ (1) и объема N[Q + ${{p}_{{q*}}}$] входных данных (2), определяющие вычислительную сложность алгоритма поиска субоптимального управления в процессе эксплуатации системы.
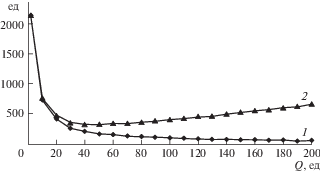
Минимальное значение вычислительной сложности алгоритма поиска субоптимального управления в процессе эксплуатации системы достигается при количестве кластеров Q = 50, максимальном количестве элементов ${{p}_{{q*}}} = 57$ и соответствующем им объеме входных данных N[Q + ${{p}_{{q*}}}$] = 321 ед.
Известно, что вычислительная сложность алгоритма поиска значения в неотсортированном N-мерном массиве из L элементов методом полного перебора составляет O(NL) и имеет линейное время. Тогда для метода полного перебора значение вычислительной сложности пропорционально объему входных данных NL = 3993 ед.
Имеем следующее. Для решения задачи поиска субоптимального управления в матрице ${{{\Psi }}_{{LH}}}$ с использованием однократной кластеризации при проектировании системы и последующим поиском среди элементов кластера с ближайшим центром в процессе эксплуатации системы для рассматриваемого примера позволяет уменьшить объем входных данных на 91.96% по сравнению с методом полного перебора, что при линейном времени работы последнего повлечет за собой существенное повышение эффективности в плане быстродействия. Фактическое же количество секунд работы алгоритма будет полностью обуславливаться архитектурой и основными характеристиками вычислительного устройства системы управления – становится меньше (больше) при переносе на более быстрое (медленное) вычислительное устройство.
При количестве кластеров Q = 50 максимальное количество элементов ${{p}_{{q*}}}$ = 57 находится в q* = 27 кластере. Тогда результаты поиска ${{\bar {x}}_{{l*}}}$, ближайшего к ${{\bar {x}}^{{measured}}}$, имеют следующую графическую интерпретацию (рис. 5а).
Рис. 5.
Графическая интерпретация поиска ${{\bar {x}}_{{l*}}}$, ближайшего к $\bar {x}_{{}}^{{measured}}$ (а) и средние значения толщины покрытия $\bar {\delta }$ на поверхности Sc шеек 1–9 (б).
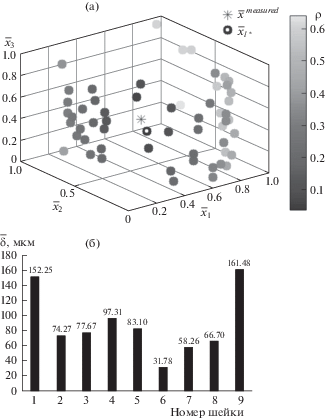
Ближайшим к значению ${{\bar {x}}^{{measured}}}$ является ${{\bar {x}}_{{l*}}}$ = (0.285; 0.198; 0.546) с индексом l* = = 392 в матрице ${{{\Psi }}_{{LH}}}$ и расстоянием ${{{\rho }}_{{l*}}}({{\bar {x}}_{{l*}}},{{\bar {x}}^{{measured}}})$ = 0.035989. Для ${{\bar {x}}_{{l*}}}$ вектор оптимальных управляющих воздействий имеет значение $u_{{l*}}^{*}$ = (1802.3; 300; 1802.3; 25), применение которого для ${{\bar {x}}^{{measured}}}$ дает средние значения толщины покрытия $\bar {\delta }$ на поверхности Sc шеек 1–9 (рис. 5б) и обеспечивает потерю в критерии равномерности ${\delta }J_{{{{x}^{{measured}}}}}^{*}$ = 8.63%.
Заключение. Использование алгоритмов с уменьшенной вычислительной сложностью для поиска субоптимального управления позволит снизить стоимость конечного управляющего устройства, а также увеличить эффективность существующего устройства за счет перераспределения освободившихся ресурсов под другие задачи, тем самым снижая его (устройства) энергопотребление или повышая производительность, что в конечном итоге позволит совершенствовать соответствующий технологический процесс изготовления конструкций машин и механизмов.
Список литературы
Ганиев Р.Ф. О современном состоянии и перспективах развития ИМАШ РАН. Проблемы механики машин и прорывных технологий // Проблемы машиностроения и надежности машин. 2014. № 3. С. 11.
Ганиев Р.Ф., Глазунов В.А. Манипуляционные механизмы параллельной структуры и их приложения в современной технике // Доклады Академии наук. 2014. Т. 459. № 4. С. 428.
Ганиев Р.Ф., Ревизников Д.Л., Сухарев Т.Ю., Украинский Л.Е. Оптимизация пространственного расположения рабочих элементов в установках колебательного типа // Проблемы машиностроения и надежности машин. 2018. № 1. С. 3.
Ганиев Р.Ф., Ревизников Д.Л., Сухарев Т.Ю., Украинский Л.Е. Профилирование поверхностей рабочих элементов перемешивающих устройств // Проблемы машиностроения и надежности машин. 2019. № 3. С. 3.
Антонов А.В., Глазунов В.А., Алешин А.К., Рашоян Г.В., Лактионова М.М. Кинематический анализ механизма параллельной структуры для работы в агрессивных средах // Проблемы машиностроения и надежности машин. 2018. № 2. С. 3.
Fomin A., Ivanov W., Glazunov V. Design and analysis of a mechanism for spherical surface processing // Mechanisms and Machine Science. 2020. V. 78. P. 39.
Rashoyan G.V., Aleshin A.K., Antonov A.V., Gavrilina L.V., Glazunov V.A., Skvortsov S.A., Shalyu-khin K.A. Analysis and synthesis of parallel structure mechanism without singularities // Journal of Physics: Conference Series. 2019. № 1260(11). P. 112023.
Поляк Б.Т., Хлебников М.В., Щербаков П.С. Разреженная обратная связь в линейных системах управления // Автоматика и телемеханика. 2014. № 12. С. 13.
Поляк Б.Т., Тремба А.А., Хлебников М.В., Щербаков П.С., Смирнов Г.В. Большие отклонения в линейных системах при ненулевых начальных условиях // Автоматика и телемеханика. 2015. № 6. С. 18.
Поляк Б.Т., Смирнов Г.В. Переходные процессы в матричных дискретных линейных системах // Автоматика и телемеханика. 2019. № 9. С. 112.
Горобцов А.С., Статников Р.Б., Солоденков С.В. Задача оптимизации виброизоляции машин с учетом разброса значений параметров // Машиностроение и инженерное образование. 2006. № 4 (9). С. 2.
Статников Р.Б., Матусов И.Б. О недопустимых, допустимых и оптимальных решениях в задачах проектирования // Проблемы машиностроения и надежности машин. 2012. № 4. С. 10.
Statnikov R.B., Gavriushin S.S., Dang M., Statnikov A. Multicriteria design of composite pressure vessels // International Journal of Multicriteria Decision Making. 2014. T. 4. № 3. C. 252.
Ghavihaa N., Bohlinb M., Wallina F., Dahlquista E. Optimal Control of an EMU Using Dynamic Programming // Energy Procedia. 2015. V. 75. P. 1913.
Пантелеев А.В., Родионова Д.А. Применение итерационного динамического программирования в задачах синтеза оптимального управления с полной обратной связью // Научный вестник Московского государственного технического университета гражданской авиации. 2016. № 224 (2). С. 5.
Босов А.В., Стефанович А.И. Управление выходом стохастической дифференциальной системы по квадратичному критерию. II. Численное решение уравнений динамического программирования // Информатика и ее применения. 2019. Т. 13. № 1. С. 9.
Гамкрелидзе Р.В. Двойственная формулировка принципа максимума Понтрягина в оптимальном управлении // Труды Математического института имени В.А. Стеклова. 2015. Т. 291. С. 69.
Никольский М.С., Беляевских Е.А. Принцип максимума Л.С. Понтрягина для некоторых задач оптимального управления пучками траекторий // Вестник Санкт-Петербургского университета. Прикладная математика. Информатика. Процессы управления. 2018. Т. 14. № 1. С. 59.
Сумин М.И. Регуляризованные принцип Лагранжа и принцип максимума Понтрягина в оптимальном управлении и обратных задачах // Труды института математики и механики УрО РАН. 2019. Т. 25. № 1. С. 279.
Щеглов Б.А. Частное решение осесимметричной задачи теории пластичности // Проблемы машиностроения и надежности машин. 2013. № 1. С. 28.
Баничук Н.В., Иванова С.Ю., Макеев Е.В., Синицын А.В. Оптимальное подавление колебаний движущегося упругого полотна // Прикладная математика и механика. 2018. Т. 82. № 2. С. 261.
Дутов А.В., Литовка Ю.В., Нестеров В.А., Соловьев Д.С., Соловьева И.А., Сыпало К.И. Поиск оптимального управления токовыми режимами в гальванических процессах со многими анодами при разнообразии номенклатуры обрабатываемых изделий // Известия Российской академии наук. Теория и системы управления. 2019. № 1. С. 78.
Дивеев А.И., Шмалько Е.Ю. Синтез системы управления на основе аппроксимации множества оптимальных траекторий методом сетевого оператора // Надежность и качество сложных систем. 2014. № 4 (8). С. 3.
Ибрагимов Д.Н. Аппроксимация множества допустимых управлений в задаче быстродействия линейной дискретной системой // Труды МАИ. 2016. № 87. С. 20.
Dashkovskiy S., Kichmarenko O., Sapozhnikova K. Approximation of Solutions to the Optimal Control Problems for Systems with Maximum // Journal of Mathematical Sciences. 2019. V. 243. Iss. 2. P. 192.
Албагачиев А.Ю. Эффективные покрытия деталей машин // Упрочняющие технологии и покрытия. 2012. № 8 (92). С. 18.
ГОСТ 9.302-88 Единая система защиты от коррозии и старения. Покрытия металлические и неметаллические неорганические. Методы контроля. М.: ИПК Издательство стандартов, 1990. 40 с.
Соловьев Д.С., Потлов А.Ю., Литовка Ю.В. Снижение неравномерности распределения толщины гальванического покрытия с использованием отключаемых анодных секций при реверсировании тока // Теоретические основы химической технологии. 2019. Т. 53. № 1. С. 102.
Fahad Sk. A Modified K-Means Algorithm for Big Data Clustering // International Journal of Computer Science Engineering and Technology. 2016. V. 6. P. 129.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин