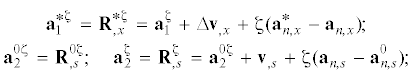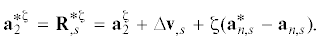Проблемы машиностроения и надежности машин, 2020, № 6, стр. 69-81

Теория оболочек в настоящее время имеет достаточно законченные очертания [1, 2]. Особо важное внимание ведущих исследователей мира, занимающихся анализом напряженно-деформированного состояния оболочечных конструкций, занимает учет физической нелинейности материала [3–5]. Применение метода конечных элементов (МКЭ) в этом случае является практически безальтернативным. Развитию, совершенствованию и использованию МКЭ посвящены работы известных отечественных и зарубежных авторов и научные статьи последних лет [6–13], изучение и анализ которых позволяет выделить ряд проблем и определить цель настоящего исследования. Во всех анализируемых литературных источниках, при учете физической нелинейности приращения деформации на шагах нагружения подразделяются на упругую и пластическую части. В настоящей статье получены зависимости между приращениями деформаций и приращениями напряжений на шаге нагружения без разделения приращений деформаций на упругую и пластическую части. В анализируемых статьях связь между средним линейным напряжением и средней линейной деформацией осуществляется при использовании условия несжимаемости материала при пластических деформациях. Это не вполне соответствует физическому смыслу процесса деформирования и может приводить к неточностям при значительных величинах пластических деформаций. В настоящей статье, при выводе уравнений связи между деформациями и напряжениями на основании деформационной теории использовалась эмпирическая функциональная зависимость между средним линейным напряжением и средней линейной деформацией на шаге нагружения.

Материалы и методы. Геометрия оболочки. Точка срединной поверхности оболочки в процессе деформирования рассматривается в трех положениях: исходное (точка ${{М}^{0}}$), деформированное положение после ( j – 1) шагов нагружения (точка M, вектор перемещения v) и положение после j-го шага нагружения (точка M*, вектор перемещения ∆v). Положение точки в произвольном слое оболочки, отстоящем на расстоянии ζ от срединной поверхности, обозначаются символами: M^0ζ, M^ζ и M*^ζ соответственно указанным состояниям.

Положение точки M⁰ эллиптического цилиндра определяется радиус-вектором

где х – осевая координата; t – параметр; 2b и 2c – размеры осей эллипса.

Дифференцированием (1) по координате х и дуге поперечного сечения эллиптического цилиндра s можно получить векторы локального базиса

где $k = \sqrt {{{b}^{2}}{{{\cos }}^{2}}t + {{c}^{2}}{{{\sin }}^{2}}t} $.

Орт нормали к срединной поверхности определяется векторным произведением

Производные векторов локального базиса можно определить дифференцированием (2) и (3)

где ${{k}_{{,t}}} = \frac{{({{c}^{2}} - {{b}^{2}})\sin 2t}}{{2k}}$; ${{t}_{{,s}}} = \frac{1}{k}$.

Соотношения (2)–(4) можно представить в матричном виде

где ${{\{ {{{\mathbf{a}}}^{0}}\} }^{T}} = \{ {\mathbf{a}}_{1}^{0};{\mathbf{a}}_{2}^{0};{\mathbf{a}}_{n}^{0}\} $; ${{\{ {\mathbf{a}}_{{,x}}^{0}\} }^{T}} = \{ {\mathbf{a}}_{{1,x}}^{0};{\mathbf{a}}_{{2,x}}^{0};{\mathbf{a}}_{{n,х}}^{0}\} $; ${{\{ {\mathbf{a}}_{{,s}}^{0}\} }^{T}} = \{ {\mathbf{a}}_{{1,s}}^{0};{\mathbf{a}}_{{2,s}}^{0};{\mathbf{a}}_{{n,s}}^{0}\} $; ${{\{ {\mathbf{i}}\} }^{T}} = \{ {\mathbf{i}};{\mathbf{j}};{\mathbf{k}}\} $.

На основании соотношения

производные векторов локального базиса представляются компонентами в этом же базисе где $[n] = \left[ {\begin{array}{*{20}{c}} 0&0&0 \\ 0&0&{{{n}_{{23}}}} \\ 0&{{{n}_{{32}}}}&0 \end{array}} \right];\;\begin{array}{*{20}{c}} {{{n}_{{23}}} = \frac{{ - cb}}{{k\sqrt k }};} \\ {{{n}_{{32}}} = \frac{{cb}}{{k\sqrt k }}.} \end{array}$

Положения точек M⁰, M, M*, M^0ζ, M^ζ и M*^ζ характеризуются радиус-векторами

где ${{{\mathbf{a}}}_{{\mathbf{n}}}}$ и ${\mathbf{a}}_{{\mathbf{n}}}^{*}$ – орты нормалей к срединной поверхности оболочки в точках M и M*.

Входящие в (6) векторы перемещений v и Δv определяются в локальном базисе выражениями

Базисные векторы в точках M^0ζ, M^ζ и M*^ζ находятся дифференцированием (6) по глобальным координатам х и s

Производные вектора v за ( j – 1) шагов нагружения можно получить дифференцированием (7) с учетом (5)

где $z_{s}^{2}$ = ${{{v}}_{{,s}}} + {{n}_{{32}}}w$; ${{z}_{s}} = {{w}_{{,s}}} + {{n}_{{23}}}{v}$; ${{z}_{{ss}}} = {{n}_{{32}}}{{n}_{{23}}}w - {{n}_{{22}}}{{n}_{{23}}}{v} + 2{{n}_{{23}}}{{{v}}_{{,s}}} + {{w}_{{,ss}}}$; $z_{{ss}}^{2}$ = = $({{n}_{{32}}}{{n}_{{23}}} + {{({{n}_{{22}}})}^{2}}){v}$ + ${{{v}}_{{,ss}}}$ + $2{{n}_{{32}}}{{w}_{{,s}}}$ + ${{n}_{{32}}}{{n}_{{22}}}w$; $z_{{xs}}^{2} = {{{v}}_{{,xs}}} + {{n}_{{22}}}{{{v}}_{{,x}}} + {{w}_{{,x}}}{{n}_{{32}}}$; ${{z}_{{xs}}} = {{n}_{{23}}}{{{v}}_{{,x}}} + {{w}_{{,xs}}}$.

Аналогично, на j-м шаге нагружения

Орты нормалей в точках M и M* выражаются векторными произведениями

где ${{{\mathbf{a}}}_{1}} = {{({{{\mathbf{R}}}^{0}} + {\mathbf{v}})}_{{,x}}}$; ${{{\mathbf{a}}}_{2}} = {{({{{\mathbf{R}}}^{0}} + {\mathbf{v}})}_{{,s}}}$; ${\mathbf{a}}_{1}^{*} = {{({\mathbf{R}} + \Delta {\mathbf{v}})}_{{,x}}}$; ${\mathbf{a}}_{2}^{*} = {{({\mathbf{R}} + \Delta {\mathbf{v}})}_{{,s}}}$.

Для определения деформаций и их приращений в произвольном слое, отстоящем на расстоянии ζ от срединной поверхности оболочки, используются уравнения механики сплошной среды [14]

где ковариантные компоненты метрических тензоров для исходного и деформированного состояний определяются выражениями

Деформации и их приращения при учете (12) и (8)–(11) запишутся как

Соотношения (13) можно представить в более компактной форме

где ε_αβ и χ_αβ – деформации и искривления срединной поверхности в точке М; Δε_αβ и Δχ_αβ – приращения деформаций и искривлений в точке М*.

Выражения (14) удобно использовать в матричном виде

где ${{\{ \varepsilon \} }^{Т}} = \{ {{\varepsilon }_{{11}}};{{\varepsilon }_{{22}}};2{{\varepsilon }_{{12}}};{{\chi }_{{11}}};{{\chi }_{{22}}};2{{\chi }_{{12}}}\} $; ${{\{ \vartheta \} }^{Т}} = \{ u;{v};w\} $; ${{\{ \Delta \varepsilon \} }^{Т}}$ = $\{ \Delta {{\varepsilon }_{{11}}};\Delta {{\varepsilon }_{{22}}};2\Delta {{\varepsilon }_{{12}}}$; Δχ₁₁; Δχ₂₂; $2\Delta {{\chi }_{{12}}}\} $; ${{\{ \Delta \vartheta \} }^{Т}} = \{ \Delta u;\Delta {v};\Delta w\} $; [L] – матрица дифференциальных и алгебраических операторов.

Конечный элемент на шаге нагружения. В качестве элемента дискретизации принимается произвольный четырехугольный фрагмент срединной поверхности оболочки с узлами i, j, k, l. Для реализации численного интегрирования выбирается квадратный в плане элемент с локальными координатами ξ и η, на который отображается выбранный криволинейный конечный элемент (КЭ). Координаты ξ и η изменяются в пределах: –1 ≤ ξ ≤ 1, –1 ≤ η ≤ 1.

Глобальные координаты х и s произвольной точки срединной поверхности являются функциями локальных координат ξ и η

где xⁱ, x ^j, …, s^k, s^l – узловые значения глобальных координат.

Зависимости (16) можно представить в матричном виде

где $\{ {{x}^{m}}\} = \{ {{x}^{i}}{{x}^{j}}{{x}^{k}}{{x}^{l}}\} $; $\{ {{s}^{m}}\} = \{ {{s}^{i}}{{s}^{j}}{{s}^{k}}{{s}^{l}}\} $.

Производные глобальных координат в локальной системе определяются в результате дифференцирования (17)

Для определения производных локальных координат в глобальной системе соотношения (17) записываются следующим образом

Дифференцированием (18) по x и по дуге s можно получить матричные зависимости

где .

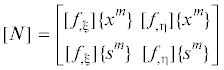Таким образом, производные локальных координат ξ и η в глобальной системе определяются соотношениями

Или в более компактной форме

где $\Delta = [{{f}_{{,\xi }}}]\{ {{x}^{m}}\} [{{f}_{{,\eta }}}]\{ {{s}^{m}}\} - [{{f}_{{,\xi }}}]\{ {{s}^{m}}\} [{{f}_{{,\eta }}}]\{ {{x}^{m}}\} $.

В качестве узловых неизвестных за ( j – 1) предыдущих шагов выбираются компоненты вектора перемещения и их производные в локальной и глобальной системах координат

где под q понимается перемещение u, $v$ или w$.$

Аналогично, на  j-м шаге нагружения

где символом Δq обозначается перемещение Δu, $\Delta v$ или Δw.

Векторы узловых неизвестных КЭ на шаге нагружения в локальной и глобальной системах координат записываются строками

На основании дифференциальных зависимостей

между узловыми неизвестными имеет место матричное соотношение

Перемещения внутренней точки КЭ в деформированном состоянии выражаются через узловые значения

где под q понимается перемещение u, $v$ или w, а элементами матрицы {φ}^T являются полиномы Эрмита третьей степени [15].

Приращения деформаций на шаге нагружения, согласно (15) и с учетом (20), перепишутся в виде

где $\mathop {[A]}\limits_{3 \times 36} = \left[ {\begin{array}{*{20}{c}} {{{{\mathop {{\text{\{ }}\varphi {\text{\} }}}\limits_{1 \times 12} }}^{T}}}&{{{{\mathop {\{ 0\} }\limits_{1 \times 12} }}^{T}}}&{{{{\mathop {\{ 0\} }\limits_{1 \times 12} }}^{T}}} \\ {{{{\mathop {\{ 0\} }\limits_{1 \times 12} }}^{T}}}&{{{{\mathop {{\text{\{ }}\varphi {\text{\} }}}\limits_{1 \times 12} }}^{T}}}&{{{{\mathop {\{ 0\} }\limits_{1 \times 12} }}^{T}}} \\ {{{{\mathop {\{ 0\} }\limits_{1 \times 12} }}^{T}}}&{{{{\mathop {\{ 0\} }\limits_{1 \times 12} }}^{T}}}&{{{{\mathop {{\text{\{ }}\varphi {\text{\} }}}\limits_{1 \times 12} }}^{T}}} \end{array}} \right]$.

Соотношения между приращениями деформаций и приращениями напряжений на шаге нагружения. При использовании основных положений деформационной теории пластичности [16] связь между компонентами девиатора деформаций и компонентами девитора напряжений осуществляется в виде

где ${{\varepsilon }_{0}} = \frac{{\varepsilon _{{11}}^{\zeta } + \varepsilon _{{22}}^{\zeta } + \varepsilon _{{33}}^{\zeta }}}{3}$ – средняя линейная деформация; ${{\sigma }_{0}} = \frac{{{{\sigma }_{{11}}} + {{\sigma }_{{22}}}}}{3}$ – среднее линейное напряжение.

На основе диаграмм растяжения и деформирования материала имеют место соотношения

где σ, ε – напряжение и деформация стержня при растяжении; μ – коэффициент поперечной деформации; Δσ, Δε – приращения напряжений и приращения деформаций на шаге растяжения стержня; σ₀, ε₀ – средние значения напряжений и деформаций; Δσ₀, Δε₀ – приращения средних значений напряжений и деформаций на шаге растяжения стержня.

Соотношения между средними деформациями и средними напряжениями определяются выражением

где E_s – секущий модуль диаграммы растяжения.

В деформационной теории пластичности принято, что за пределами упругости зависимость ε₀ от σ₀ остается неизменной

где ${{K}_{1}} = \frac{{1 - 2\mu }}{E}$; E – модуль упругости.

На основе (24) и с учетом (23) можно получить зависимости

где E_sd – секущий модуль диаграммы деформирования материала; E_h – хордовый модуль диаграммы деформирования.

Для определения компонент приращений тензора деформаций на шаге нагружения необходимо выразить из (22) деформации в явном виде

где α = 1, 2.

В общем случае приращения деформаций на шаге нагружения определяются соотношением

В настоящей статье для получения зависимостей между приращениями деформаций и напряжений предлагается использовать гипотезу о пропорциональности компонент девиаторов приращений деформаций компонентам девиаторов приращений напряжений на шаге нагружения

На основании (25)–(29) формируется матричная зависимость

где m = 1, 2, 3; ${{\{ \Delta {{\varepsilon }^{\zeta }}\} }^{T}} = \{ \Delta \varepsilon _{{11}}^{\zeta }\Delta \varepsilon _{{22}}^{\zeta }2\Delta \varepsilon _{{12}}^{\zeta }\} $; ${{\{ \Delta {{\sigma }_{{\alpha \beta }}}\} }^{T}} = \{ \Delta {{\sigma }_{{11}}}\Delta {{\sigma }_{{22}}}\Delta {{\sigma }_{{12}}}\} $; $[{{D}_{m}}]$ – матрица упругопластического деформирования на шаге нагружения на основе коэффициентов K₁, K₂ и K₃ соответственно.

Матрица жесткости на шаге нагружения. При выводе матрицы жесткости четырехугольного КЭ используется функционал, основанный на равенстве работ внутренних и внешних сил на шаге нагружения

где ${{\{ {{\sigma }_{{\alpha \beta }}}\} }^{Т}} = \{ {{\sigma }_{{11}}}{{\sigma }_{{22}}}{{\sigma }_{{12}}}\} $ – матрица-строка напряжений после ( j – 1) шагов нагружения в произвольном слое оболочки, отстоящем на расстоянии ζ от срединной поверхности; ${{\{ P\} }^{Т}}$ = $\{ {{P}_{{11}}}{{P}_{{22}}}{{P}_{{12}}}\} $; ${{\{ \Delta P\} }^{Т}}$ $\{ \Delta {{P}_{{11}}}\Delta {{P}_{{22}}}\Delta {{P}_{{12}}}\} $ – внешняя нагрузка за ( j – 1) предыдущих шагов нагружения и ее приращения на  j-м шаге нагружения.

Для точки произвольного слоя, отстоящего на расстоянии ζ от срединной поверхности оболочки, приращения напряжений определяются соотношением

где ${{\mathop {[{{D}_{m}}]}\limits_{3 \times 3} }^{{ - 1}}}$ выражается из (30).

С учетом (21) и (32) равенство (31) можно записать в виде

При использовании (19) и выполнении минимизации (33) по узловым неизвестным $\{ \Delta U_{y}^{g}\} $ формируется матричное соотношение

где $\mathop {[M]}\limits_{36 \times 36} = {{\mathop {[H]}\limits_{36 \times 36} }^{Т}}\int_V {{{{\mathop {[B]}\limits_{36 \times 6} }}^{T}}} {{\mathop {[G]}\limits_{6 \times 3} }^{Т}}{{\mathop {[{{D}_{m}}]}\limits_{3 \times 3} }^{{ - 1}}}\mathop {[G]}\limits_{3 \times 6} \mathop {[B]}\limits_{6 \times 36} dV\mathop {[H]}\limits_{36 \times 36} $ – матрица жесткости четырехугольного КЭ на шаге нагружения;

$\mathop {\{ F\} }\limits_{36 \times 1} = {{\mathop {[H]}\limits_{36 \times 36} }^{Т}}\int_F {{{{\mathop {[A]}\limits_{36 \times 3} }}^{T}}\mathop {\{ \Delta P\} }\limits_{3 \times 1} dF} $ – вектор узловых нагрузок на шаге нагружения;

$\mathop {\{ f\} }\limits_{36 \times 1} = {{\mathop {[H]}\limits_{36 \times 36} }^{Т}}\int_F {{{{\mathop {[A]}\limits_{36 \times 3} }}^{T}}} \mathop {\{ P\} }\limits_{3 \times 1} dF - {{\mathop {[H]}\limits_{36 \times 36} }^{Т}}\int_V {{{{\mathop {[B]}\limits_{36 \times 6} }}^{T}}} {{\mathop {[G]}\limits_{6 \times 3} }^{Т}}\mathop {\{ {{\sigma }_{{\alpha \beta }}}\} }\limits_{3 \times 1} dV~$ – поправка Ньютона–Рафсона.

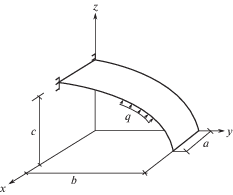
Результаты. В качестве примера была решена тестовая задача по определению напряженно-деформированного состояния фрагмента произвольной оболочки в форме эллиптического цилиндра (рис. 1).

Оболочка, загруженная внутренним давлением интенсивности q, имеет на левом крае жесткое защемление. Были приняты следующие исходные данные: q = 0.18 МПа; модуль упругости E = 2 × 10⁶ МПа; коэффициент Пуассона μ = 0.32; толщина оболочки t = 0.005 м; интенсивность напряжения, соответствующая пределу текучести σ_iT  = 200 МПа; интенсивность деформации, соответствующая пределу текучести ε_iT  = 0.0023; геометрические характеристики оболочки: a = b = 1 м, c = 0.5 м.

С учетом условия сходимости вычислительного процесса на первом шаге нагружения при различных вариантах дискретизации оболочки было принято достаточным разбиение рассматриваемой конструкции на двадцать шесть четырехугольных КЭ.

В настоящей статье диаграмма деформирования для нелинейного участка аппроксимировалась в виде функции

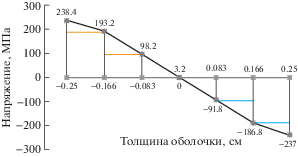
где А = –23461.55 МПа; В = 181201.17 МПа; С = 1574.3 МПа.

При решении задачи было реализовано три различных варианта расчета. В первом варианте зависимости между напряжениями и деформациями на шаге нагружения формировались при использовании коэффициента ${{K}_{1}} = \frac{{1 - 2{\mu }}}{E}$. В табл. 1 приведены результаты конечно-элементных решений для данного варианта расчета при различных числах шагов нагружения. Значения напряжений σ₂₂ представлены для жестко защемленного левого и незагруженного правого края оболочки в зависимости от координаты ζ по толщине оболочки.

Во втором варианте расчета для связи средней линейной деформации ε₀ и среднего линейного напряжения σ₀ на шаге нагружения использовался коэффициент K₂ = = $\frac{{3(1 - 2\mu )}}{{2(1 + \mu )}}\frac{{{{\varepsilon }_{i}}}}{{{{\sigma }_{i}}}}$. Значения контролируемых параметров напряженно-деформированного состояния для второго варианта представлены в табл. 2.

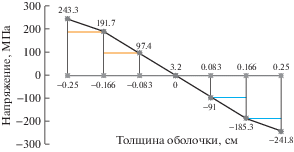
В третьем варианте расчета разделение деформации на шаге нагружения на упругую и пластическую части не использовалось. Приращения компонент тензора деформаций определялись согласно (29), что значительно упростило алгоритм формирования матрицы пластичности. В табл. 3 представлены значения напряжений σ₂₂ для контролируемых точек оболочки в третьем варианте расчета.

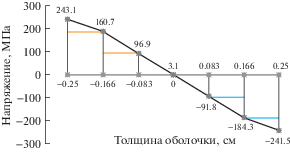
С использованием полученных данных, в опорном сечении при числе шагов n = 100, были построены эпюры напряжений σ₂₂ по толщине рассматриваемой оболочки. Данные эпюры для трех вариантов расчета представлены на рис. 2–4.

Обсуждения. Анализ полученных результатов производился по нескольким критериям. При различном числе шагов нагружения сравнивались численные значения напряжений σ₂₂ в рассматриваемых сечениях оболочки: левом, жестко защемленном крае и в концевом сечении.

Как видно из табл. 1–3 во всех вариантах расчета наблюдается удовлетворительная сходимость вычислительного процесса. С ростом числа шагов нагружения значения контролируемых параметров напряженно-деформированного состояния незначительно (в пределах 1%) отличаются друг от друга.

Так как правый край оболочки не загружен и по физическому смыслу задачи значения напряжений σ₂₂$~$на срединной поверхности в этом сечении должны стремиться к нулю. Нормальные напряжения σ₂₂ на срединной поверхности правого края стремятся к нулю, что соответствует физическому условию нагружения рассматриваемой конструкции (табл. 1–3).

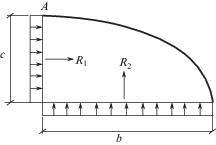
Для получения третьего критерия верификации полученных данных необходимо вычислить изгибающий момент в опорном сечении рассматриваемой конструкции и сравнить его со значением, вычисленным из условия статики. Согласно расчетной схеме (рис. 5), суммарный изгибающий момент относительно точки А находится как

Во всех трех вариантах расчета при числе шагов равном n = 100 в опорном сечении были получены численные значения расчетных изгибающих моментов. Для этого, эпюры кольцевых напряжений разбивались на элементарные геометрические фигуры и вычислялись их площади. Затем полученные усилия умножались на соответствующие плечи, равные расстояниям от центров тяжести элементарных фигур до нейтральной оси сечения оболочки. Суммированием полученных произведений находились расчетные значения изгибающих моментов для каждого из вариантов расчета.

Для первого варианта расчета суммарный изгибающий момент оказался равным $М_{1}^{R} = 10.986$ кН м, для второго варианта $М_{2}^{R} = 10.995$ кН м, а в третьем варианте расчета данное значение составило $М_{3}^{R} = 11.03$ кН м. Сравнивая полученные значения с результатом (34), можно определить погрешности вычислений, которые составили ${{{\delta }}_{1}} = 2.34\% $, ${{{\delta }}_{2}} = 2.26\% $ и ${{{\delta }}_{3}} = 1.91\% $ соответственно для каждого из вариантов.

Заключение. Опираясь на анализ полученных результатов можно сделать несколько выводов: 1) разработанный алгоритм учета физической нелинейности материала можно эффективно использовать в расчетах произвольных оболочек, т.к. доказана возможность получения достоверных значений контролируемых параметров напряженно-деформированного состояния при различных вариантах компоновки матрицы пластичности на шаге нагружения; 2) использование предположения о неизменности объема в результате пластических деформаций является, по мнению авторов, не совсем корректным. Сравнительный анализ показал, что связь между первыми инвариантами тензоров деформаций и напряжений на шаге нагружения можно осуществлять в виде (26), что более соответствует физическому смыслу процесса деформирования; 3) доказано, что предположение о неразделении приращения деформации на упругую и пластическую части на шаге нагружения обосновано. Использование соотношений (29) позволило исключить процедуру дифференцирования зависимостей полных деформаций от напряжений, что существенно упрощает процесс формирования матрицы пластичности на шаге нагружения. Третий вариант расчета позволил получить наименьшую погрешность вычислений.