Проблемы машиностроения и надежности машин, 2020, № 6, стр. 16-34

Роботы параллельной структуры находят все большее применение в промышленности, в том числе машиностроении для выполнения различных технологических операций. Такие роботы обладают высокой производительностью, имеют повышенную жесткость конструкции, точность выполняемых операций. Вопросы структурного синтеза, методы исследования рабочего пространства, оптимизации траектории движения таких механизмов подробно рассмотрены в [1–4]. Важной характеристикой роботов параллельной структуры является их рабочая область, в пределах которой должен находиться рабочий инструмент при выполнении технологических операций. Нахождение рабочей области таких роботов гораздо сложнее, чем для роботов с последовательной архитектурой, что связано с особенностями структуры, кинематики и динамики. Для определения рабочей области известно применение различных численных методов интервального анализа, сеточной аппроксимации [5]. Применение традиционных подходов для решения поставленной задача связано со значительными вычислительными трудностями, т.к. задача имеет большую размерность, что практически нереализуемо с использованием вычислительной техники. В работе [6] рассмотрен метод неравномерных покрытий для аппроксимации множества решений системы нелинейных неравенств, а в [7–9] этот метод применялся для определения рабочей области некоторых типов планарных роботов. Покрытием множества P называем совокупность n-мерных параллелепипедов P_i, $i \in \overline {1,k} $, таких, что $P \subseteq \bigcup\nolimits_{i \in \overline {1,k} } {{{P}_{i}}} $ и для каждого P_i, $i \in \overline {1,k} $, выполняется хотя бы одно из трех условий

3. неравенства (1) и (2) не выполняются и d(P_i) ≤ δ, где δ – заданная положительная величина, определяющая точность аппроксимации.

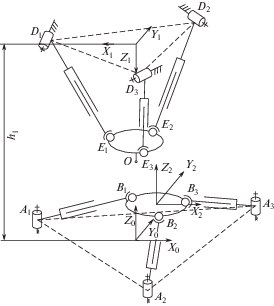
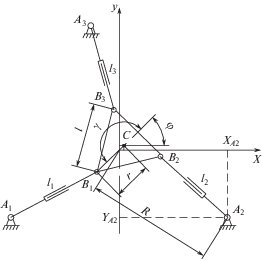
На основе метода неравномерных покрытий строится внешнее и внутреннее аппроксимационные множества. Внутреннее аппроксимационное множество включается во множество решений системы неравенств, а внешнее включает его. Оба множества представляют собой объединения n-мерных параллелепипедов. Этот метод позволяет аппроксимировать множество решений систем равенств или неравенств, описывающих рабочую зону робота. Рассмотрим структуру робота с механизмами относительного манипулирования (ОМ), в котором в отличие от [10], вращательные приводные пары верхнего и нижнего модулей заменены на поступательные (рис. 1). Верхний модуль выполнен на основе трипода с приводными поступательными кинематическими парами и вращательными шарнирами D₁, D₂, D₃ и сферическими шарнирами E₁, E₂, E₃. Центр подвижной платформы модуля-трипода может совершать поступательное перемещение по оси Z и вращательное вокруг осей X и Y, а также дополнительные смещения выходного звена при его поворотах относительно горизонтальных осей, налагаемых кинематическими цепями модуля-трипода. Нижний модуль выполнен на основе плоского 3-RРR-механизма с поступательными приводными кинематическими парами и вращательными шарнирами ${{A}_{1}}$, ${{A}_{2}}$, ${{A}_{3}}$ совершает поступательное перемещение по осям X и Y, вращательное вокруг оси Z$.$ Таким образом, робот с механизмами ОМ имеет шесть степеней свободы. Его можно использовать для выполнения операций обработки деталей, если рабочий инструмент закреплен на подвижной платформе модуля-трипода, а обрабатываемая деталь на подвижной платформе 3-RPR-механизма. Оси Z₀ и Z₁, лежат на одной прямой, перпендикулярной неподвижному основанию модуля-трипода D₁D₂D₃ и платформе плоского 3-RPR-механизма и проходящей через центр описанной окружности треугольника A₁A₂A₃. В начальном положении, то есть при совпадении центра описанной окружности треугольника A₁A₂A₃ с центром подвижной платформы плоского 3-RРR-механизма подвижная система координат X₂Y₂Z₂ совпадает с X₀Y₀Z₀.

Для построения рабочей области робота ОМ в подвижной системе координат, связанной с нижнем модулем, используем аппроксимационные множества отдельных модулей робота. Для нахождения максимума и минимума функций в параллелепипедах можно применить методы интервального анализа. Однако в этом случае, в связи с множественным вхождением переменных могут возникнуть ошибки, влияющие на результат. Поэтому поиск минимума и максимума функции находим с помощью сеточной аппроксимации. Метод аппроксимации разработан и апробирован ранее на моделях роботов с двумя и тремя степенями свободы в рамках проекта РНФ № 16-19-00148.

Определим рабочие области отдельных модулей. В статье [10] рассмотрен численный метод построения рабочей области плоских параллельных манипуляторов различной структуры, основанный на уравнениях кинематической сингулярности и управлении углами давления в шарнирах манипулятора вдоль заданной траектории платформы. В нашем случае механизм более сложный, состоящий из двух модулей, поэтому мы применяем метод, основанный на концепции неравномерных покрытий.

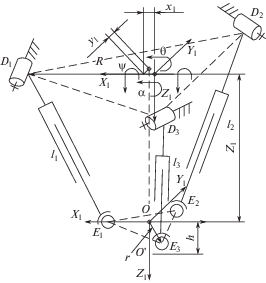
Рассмотрим схему верхнего модуля на базе трипода (рис. 2), который включает три штанги переменной длины l₁, l₂, l₃, которые соединены вращательными шарнирами D₁, D₂, D₃ с основанием и сферическими шарнирами E₁, E₂, E₃ с рабочей платформой. Основание и рабочая платформа представляют собой равносторонние треугольники. При изменении длин штанг рабочая платформа совершает перемещение по оси Z₁ на расстояние z₁, и повороты вокруг оси X₁ на угол ψ и вокруг Y₁ угол θ. Кроме этого, имеются дополнительные степени свободы – смещение по осям X₁ на расстояние x₁ и по Y₁ на расстояние y₁ и поворот относительно Z₁ на угол α, которые определяются по формулам [12]

Входными координатами являются длины приводных звеньев l₁, l₂, l₃, выходными – координаты точки O' рабочего органа ${{x}_{{o'}}}$, ${{y}_{{o'}}}$, ${{z}_{{o'}}}$. Точка O' располагается на расстоянии h от центра подвижной платформы. Для определения рабочей области необходимо предварительно определить множество допустимых значений линейных и угловых координат центра O подвижной платформы, а затем для данных значений определить множество координат O' рабочего органа. Координаты O' в подвижной системе координат $X_{1}^{'}Y_{1}^{'}Z_{1}^{'}$

Вычислим координаты точки O' в неподвижной системе координат X₁Y₁Z₁

где ${{{\mathbf{M}}}_{{1'\_1}}}$ – матрица перехода от подвижной системы координат $X_{1}^{'}Y_{1}^{'}Z_{1}^{'}$ к неподвижной системе X₁Y₁Z₁, которая включает матрицы смещений вдоль осей X₁, Y₁, Z₁ и поворотов вокруг осей X₁, Y₁, Z₁

Обозначим в (3)

После преобразования получим

Введем ограничения на геометрические параметры механизма

где l_min, l_max определяются конструктивными параметрами механизма; l_i – длина i-й штанги, которая определяется как где x_Ei, y_Ei, z_Ei – координаты центров шарниров, точка E_i; x_Di, y_Di, z_Di – координаты центров шарниров, точка D_i в неподвижной системе координат.

Определим координаты шарниров E_i в подвижной системе координат $X_{1}^{'}Y_{1}^{'}Z_{1}^{'}$ ${\mathbf{E}}_{1}^{'}$ = = ${{\left[ {\begin{array}{*{20}{c}} r&{\begin{array}{*{20}{c}} 0&{\begin{array}{*{20}{c}} 0&1 \end{array}} \end{array}} \end{array}} \right]}^{T}}$, ${\mathbf{E}}_{2}^{'}$ = ${{[\begin{array}{*{20}{c}} { - 0.5r}&{0.5\sqrt 3 r}&0&1 \end{array}]}^{T}}$, ${\mathbf{E}}_{3}^{'}$ = ${{[\begin{array}{*{20}{c}} { - 0.5r}&{ - 0.5\sqrt 3 r}&0&1 \end{array}]}^{T}}$.

Выразим координаты шарниров E_i в неподвижной системе координат X₁Y₁Z₁

где ${{y}_{1}} = - {{M}_{{21}}}r = - r\cos \psi \sin \alpha $.

Определим координаты шарниров D_i в неподвижной системе координат X₁Y₁Z₁

Подставив (6) и (7) в (5), получим

С учетом формул (4), (5), (8)–(10) синтезирован алгоритм аппроксимации рабочей области модуля-трипода. Алгоритм работает с четырьмя списками шестимерных параллелепипедов ${{\mathbb{P}}_{0}}$, ${{\mathbb{P}}_{{0,I}}}$, ${{\mathbb{P}}_{1}}$ и ${{\mathbb{P}}_{{1,I}}}$, при этом список ${{\mathbb{P}}_{0}}$ включает набор параллелепипедов, содержащих множество положений O, список ${{\mathbb{P}}_{{0,I}}}$ включает набор параллелепипедов, содержащих множество координат O, удовлетворяющих условию (5), список ${{\mathbb{P}}_{1}}$ включает набор параллелепипедов, содержащих множество положений O', список ${{\mathbb{P}}_{{0,I}}}$ включает набор параллелепипедов, содержащих множество координат O', удовлетворяющих условию (5). Алгоритм работает следующим образом:

1. Зададим геометрические параметры робота и точность аппроксимации δ.

2. На первом шаге алгоритма списки внутренней аппроксимации ${{\mathbb{P}}_{{0,I}}}$ и ${{\mathbb{P}}_{{1,I}}}$ пусты, список ${{\mathbb{P}}_{0}}$ состоит только из одного параллелепипеда Q, включающего диапазон углов ψ и θ поворота платформы $\left[ { - \frac{{\pi }}{2},\frac{{\pi }}{2}} \right]$ и высоты платформы $\left[ {{{l}_{{{\text{min}}}}},{{l}_{{{\text{max}}}}}} \right]$, а список ${{\mathbb{P}}_{1}}$ состоит только из одного параллелепипеда Q, гарантировано включающего рабочую область по осям X₁, Y₁ и Z₁.

3. Извлечем из списка ${{\mathbb{P}}_{0}}$ параллелепипед ${{Q}_{j}}$, $j \in 1,n$ и разделим равномерной сеткой по каждой из осей углов поворота θ и ψ и перемещения по оси ${{Z}_{1}}$ с шагом $\frac{{\pi }}{n}$ и $\frac{{({{l}_{{{\text{min}}}}},{{l}_{{{\text{max}}}}})}}{n}$ соответственно.

4. Определим для всех точек ${{A}_{k}}$, лежащих внутри параллелепипеда с координатами ${{z}_{k}}$, ${{{\psi }}_{k}}$, ${{{\theta }}_{k}}$, значение длин штанг l₁, l₂, l₃ по формулам (8)–(10) и координаты O' (${{x}_{{o'}}}$, ${{y}_{{o'}}}$, ${{z}_{{o'}}}$) по формуле (4).

5. Определим max и min значения координат O' – ${{x}_{{o'{\text{min}}}}}$, ${{y}_{{o'{\text{min}}}}}$, ${{z}_{{o'{\text{min}}}}}$, ${{x}_{{o'{\text{max}}}}}$, ${{y}_{{o'{\text{max}}}}}$, ${{z}_{{o'{\text{max}}}}}$.

6. Если для всех точек A_k из ${{Q}_{j}}$ выполняется условие (5), ${{Q}_{j}}$ добавляется со значениями ${{x}_{{o'{\text{min}}}}}$, ${{y}_{{o'{\text{min}}}}}$, ${{z}_{{o'{\text{min}}}}}$, ${{x}_{{o'{\text{max}}}}}$, ${{y}_{{o'{\text{max}}}}}$, ${{z}_{{o'{\text{max}}}}}$ к списку ${{\mathbb{P}}_{{0,I}}}$.

7. Если для всех точек A_k из Q_j не выполняется условие (5), Q_j исключается.

8. В остальных случаях Q_j делится на два равных параллелепипеда вдоль ребра с наибольшей длиной. Данные параллелепипеды вносятся в конец списка ${{\mathbb{P}}_{0}}$, а если $d({{Q}_{j}}) < {\delta }$ по двум осям – со значениями ${{x}_{{o'{\text{min}}}}}$, ${{y}_{{o'{\text{min}}}}}$, ${{z}_{{o'{\text{min}}}}}$, ${{x}_{{o'{\text{max}}}}}$, ${{y}_{{o'{\text{max}}}}}$, ${{z}_{{o'{\text{max}}}}}$.

9. Если $d({{Q}_{j}}) < {\delta }$ по всем осям, то переходим к шагу 11.

10. В остальных случаях происходит повторение шагов 3–9.

11. Извлекаем из списка ${{\mathbb{P}}_{1}}$ параллелепипед Q_j и разделим равномерной сеткой на n частей по каждой из осей.

12. Если ${{A}_{k}} \in {{\mathbb{P}}_{{0,I}}}$ для всех ${{A}_{k}} \in {{Q}_{j}}$, то Q_j добавляется к списку ${{\mathbb{P}}_{{1,I}}}$.

13. Если ${{A}_{k}} \notin {{\mathbb{P}}_{{0,I}}}$ для всех ${{A}_{k}} \in {{Q}_{j}}$, то Q_j исключается из рассмотрения.

14. В остальных случаях Q_j делится на два равных параллелепипеда вдоль ребра с наибольшей длиной. Параллелепипеды вносятся в конец списка ${{\mathbb{P}}_{1}}$.

15. Если d(Q_j) < δ, то алгоритм завершает свою работу.

16. В остальных случаях происходит повторение шагов 11–15.

Рабочая область представляет собой совокупность параллелепипедов из списка ${{\mathbb{P}}_{{1,I}}}$ и параллелепипедов меньше заданной точности аппроксимации δ по всем осям из списка ${{\mathbb{P}}_{1}}$.

Моделирование выполнено для ${{l}_{{1,2,3}}}$ ∈ [300 мм, 600 мм], R = 400 мм, r = 100 мм. Результаты моделирования представлены на рис. 3.

Рабочая область модуля-трипода (рис. 3) для заданных параметров ограничена размерами 226 × 260 × 621 мм. Время вычисления для точности аппроксимации δ = 2 мм и размерности сетки для вычислений функций 64 × 64 × 64 на ЭВМ составило 1 час 44 минуты.

Исследуем изменения рабочей области модуля-трипода при различных углах ориентации выходного звена ψ и θ, т.к. из рис. 3 не ясна зависимость вида и формы рабочей области модуля-трипода от ориентации выходного звена.

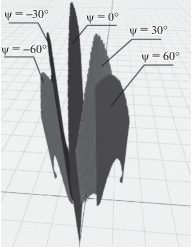
Первоначально рассмотрим вид и форму рабочей области при углах ориентации выходного звена ψ = –60°; –30°; 0°; 30°; 60°, при этом угол θ меняется в диапазоне [‒π/2, π/2]. Изменения рабочей области при различных углах ориентации ψ представлены на рис. 4.

Рабочая область модуля-трипода (рис. 4) достигает максимальных размеров при ψ = 0° и составляет 21 × 621 мм. Рабочие области являются симметричными при углах ψ = –60°, ψ = 60° и при углах ψ = –30°, ψ = 30°. При увеличении или уменьшении угла ψ габариты рабочей области уменьшаются от 212 до 102 мм по оси Х и от 621 до 492 мм по оси Z, увеличивается ее кривизна и габаритный размер по оси Y от 0 до 87 мм.

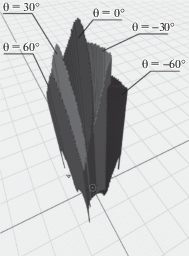
Далее рассмотрим вид и форму рабочей области при различных углах ориентации выходного звена θ = –60°; –30°; 0°; 30°; 60°, при этом угол ψ меняется в диапазоне [‒π/2, π/2]. Изменения рабочей области при различных углах ориентации θ представлены на рис. 5.

Рабочая область модуля-трипода (рис. 5) достигает максимальных размеров по оси X при θ = –60° и составляет 160 мм, по оси Y при θ = 60° и составляет 236 мм, по оси Z при θ = 30° и составляет 524 мм. При изменении угла θ от –60° до 60° уменьшается кривизна рабочей области.

Рассмотрим аналогичным образом плоский 3-RPR-механизм, который состоит из трех цепей, содержащих три штанги переменной длины, шарнирно прикрепленные к неподвижному основанию в вершинах равностороннего треугольника A₁, A₂, A₃ (рис. 6). Другие концы штанг шарнирно закреплены в вершинах равностороннего треугольника B₁, B₂, B₃ на подвижной платформе. Входными координатами являются длины штанг (l₁, l₂, l₃), выходными – положение геометрического центра подвижной платформы в декартовых координатах $(x,y)$, связанных с центром основания механизма, и угол ее поворота (φ) относительно оси, перпендикулярной плоскости основания. R и r – радиусы окружностей, описывающих треугольники ${{A}_{1}}{{A}_{2}}{{A}_{3}}$ и ${{B}_{1}}{{B}_{2}}{{B}_{3}}$ соответственно.

Определим рабочую область 3-RPR-механизма. Для этого введем ограничения на геометрические параметры механизма

где l_min, l_max определяются конструктивными параметрами механизма, l_i – текущая длина i-й штанги, которую определяем по формуле где γ_i – угол, определяющий геометрию выходного звена; x_Ai, y_Ai – координаты точки A_i – шарнира крепления штанги к неподвижному основанию; l_i – длина i-й штанги.

Если точки A_i и B_i расположены в вершинах равносторонних треугольников, то изменение длин штанг определяется по формулам

С учетом (11)–(14) синтезирован алгоритм аппроксимации рабочей области 3-RРR-механизма, которая представляет собой множество точек $C$. Алгоритм работает с двумя списками шестимерных параллелепипедов ${{\mathbb{P}}_{2}}$ и ${{\mathbb{P}}_{{2,I}}}$, при этом список ${{\mathbb{P}}_{2}}$ включает набор параллелепипедов, содержащих множество положений точки C, список ${{\mathbb{P}}_{{2,I}}}$ включает набор параллелепипедов, содержащих множество положений C, удовлетворяющих условию (11).

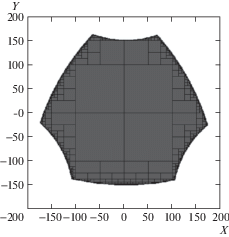
Результаты моделирования для R = 400 мм, r = 50 мм, ${{l}_{{1,2,3}}}$ ∈ [200 мм, 500 мм] представлены на рис. 7. Время вычисления для точности аппроксимации ${\delta } = 2$ мм и размерности сетки для вычислений функций 8 × 8 × 8 на персональном компьютере составило 18 секунд. Рабочая область 3-RРR-механизма для заданных параметров ограничена размерами 348 × 313 мм. Множество решений неравенств, описывающих рабочие области модуля-трипода (рис. 7) и 3-RРR-механизма, представляет собой аппроксимированный объем неправильной формы, состоящий из совокупности большого множества параллелепипедов.

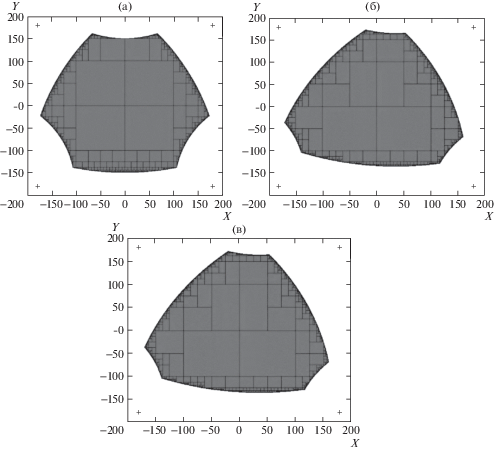
Аналогичным образом исследована зависимость вида и формы рабочей области плоского механизма от ориентации выходного звена при фиксированных значениях угла поворота φ вокруг оси Z. На рис. 8 показана рабочая область плоского 3-RРR-механизма при различных углах ориентации φ. Для заданных параметров ${{l}_{{1,2,3}}}$∈ [200 мм, 500 мм], R = 400 мм, r = 50 мм (рис. 8) размер рабочей области плоского 3-RРR-механизма уменьшается с ростом угла φ от 350 мм до 280 мм по оси X и от 300 мм до 250 мм по оси Y. При φ = 0° и φ = 45° в рабочей зоне манипулятора наблюдаются вырезы, их размер и расположение зависит от минимальной длины l_imin, чем она меньше, тем меньше и сами вырезы.

Для построения рабочей области робота с механизмами ОМ, накладывающей ограничения на геометрические параметры обрабатываемого изделия, необходимо найти множество положений O' в подвижной системе координат X₂Y₂Z₂, размещенной в центре плоского 3-RРR-механизма. При определении множества положений O' с использованием комбинаций точек из параллелепипедов, описывающих рабочие области модуля-трипода и 3-RРR-механизма, возникает необходимость вычисления координат O' значительное число раз. Например, в случае разделения параллелепипедов равномерной сеткой 100 × 100 и количества параллелепипедов в каждом из списков n = 1000, количество вычислений и результатов, которые необходимо сохранить по каждой из координат составляет 10¹⁸ раз. В связи с этим, необходимо применить “обратный” метод, т.е. проверить O' с координатами x₂, y₂, z₂ на вхождение в рабочую область модуля-трипода. Для этого определим координаты O' в неподвижной системе X₁Y₁Z₁ с использованием матриц преобразований, учитывающих переход от системы X₂Y₂Z₂ к X₁Y₁Z₁, извлекаемых из параллелепипедов, описывающих рабочую область 3-RPR-механизма. Запишем соотношение, связывающее координаты O' в системах X₂Y₂Z₂ и X₁Y₁Z₁ (рис. 2)

где ${\mathbf{O}}_{2}^{'} = {{\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{x}_{1}}}&{{{y}_{1}}} \end{array}}&{\begin{array}{*{20}{c}} {{{z}_{1}}}&1 \end{array}} \end{array}} \right]}^{T}}$ – вектор координат O' рабочего органа в неподвижной системе координат X₁Y₁Z₁; ${\mathbf{O}}_{2}^{'} = {{\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{x}_{2}}}&{{{y}_{2}}} \end{array}}&{\begin{array}{*{20}{c}} {{{z}_{2}}}&1 \end{array}} \end{array}} \right]}^{T}}$ – вектор координат O' в подвижной системе координат X₂Y₂Z₂, которые необходимо проверить на вхождение в рабочую область модуля-трипода (рис. 3); ${{{\mathbf{M}}}_{{2\_0}}}$ = $\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\cos \varphi }&{ - \sin \varphi } \\ {~\sin \varphi }&{\cos \varphi } \end{array}}&{\begin{array}{*{20}{c}} 0&{{{x}_{0}}} \\ 0&{{{y}_{0}}} \end{array}} \\ {\begin{array}{*{20}{c}} {~~~~0~~~~}&{~~~~~0~~~~} \\ 0&{~0} \end{array}}&{\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \end{array}} \right]$ – матрица, учитывающая переход от системы координат X₂Y₂Z₂ к X₀Y₀Z₀, где φ – угол поворота системы координат X₀Y₀Z₀ относительного оси Z₀; x₀, y₀ – линейные смещения по осям X₀ и Y₀ соответственно; ${{{\mathbf{M}}}_{{0\_1}}}$ = $\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} { - 1}&0 \\ {~~0}&1 \end{array}}&{\begin{array}{*{20}{c}} 0&0 \\ 0&0 \end{array}} \\ {\begin{array}{*{20}{c}} {~~~0}&{~0} \\ {~~~0}&{~0} \end{array}}&{\begin{array}{*{20}{c}} { - 1}&{{{h}_{1}}} \\ 0&1 \end{array}} \end{array}} \right]$ – матрица, учитывающая переход от системы координат X₀Y₀Z₀ к X₁Y₁Z₁, где h₁ – расстояние от центра платформы 3-RРR-механизма до центра неподвижной платформы модуля-трипода.

Тогда

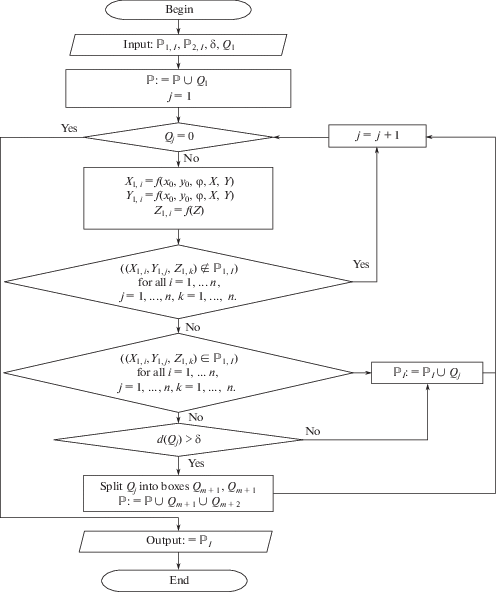
Алгоритм аппроксимации рабочей области робота с механизмами ОМ в подвижной системе координат разработан в рамках проекта РНФ № 17-79-10512, программное обеспечение – в рамках проекта РНФ № 16-19-00148. Алгоритм (рис. 9) работает с четырьмя списками трехмерных параллелепипедов: двумя полученными ранее списками ${{\mathbb{P}}_{{1,I}}}$ и ${{\mathbb{P}}_{{2,I}}}$, которые не будут изменяться в процессе выполнения алгоритма, а также двумя изменяемыми списками $\mathbb{P}$ и ${{\mathbb{P}}_{I}}$.

Результаты моделирования представлены на рис. 10. Время вычисления для точности аппроксимации ${\delta } = 6$ мм и размерности сетки для вычислений функций 64 × 64 × 64 на персональном компьютере составили 2 часа 45 минут.

Визуализация результатов моделирования рабочей области осуществляется посредством преобразования списка трехмерных параллелепипедов, описывающих рабочую область в универсальный формат 3D-моделей-STL-файл.

Реальные конструктивные параметры механизма вносят дополнительные ограничения на рабочую область. Кроме ограничений на диапазон длин звеньев рабочее пространство робота зависит также от ограничений на углы поворота шарниров, интерференции звеньев, особых положений модулей.

Исследуем влияние конструктивных ограничений реального образца робота с механизмами ОМ на вид и форму его рабочей области.

Пересечение между звеньями было рассмотрено для плоского робота в [13, 14], для кабельных роботов в [15] или для определения траекторий в глобальном планировщике движений в [16]. В [17] с учетом пересечения звеньев определена траектория движения параллельного робота с шестью степенями подвижности с приводными парами в виде цилиндров, который может двигается внутри заданного рабочего пространства или по траектории. В работе [18] с помощью геометрического метода определено рабочее пространство параллельных манипуляторов, для которых ориентация постоянна. Masory и Wang [19] представили численный метод для оценки рабочего пространства платформы Стюарта с учетом ограничений длины звеньев, ограничений угла поворота соединений и интерференции звеньев. В [20] предложен численный метод для определения рабочей области, свободной от ограничений, плоских и пространственных параллельных манипуляторов с тремя степенями свободы.

Подход, изложенный в [18], использован для разработки алгоритма построения рабочей области робота с механизмами ОМ с учетом конструктивных ограничений.

Для модуля-трипода с заданными параметрами R = 400 мм, r = 100 мм, ${{l}_{{1,2,3}}}$ ∈ [300 мм, 600 мм] кроме ограничений на длины штанг введем дополнительные конструктивные ограничения на углы поворота сферических шарниров ε₁, β₁ ≥ 5°, где ε₁ – угол между звеньями D₁E₁ и E₁E₂, β₁ – угол между звеньями D₁E₁ и E₁E₃ (рис. 11). Аналогично введем ограничения для двух других штанг на углы ε₂, ε₃ и β₂, β₃. В математической модели не учитываются реальные размеры шарниров, креплений, масса звеньев, зазоры в кинематических парах.

Для плоского 3-RPR-механизма с параметрами R = 400 мм, r = 50 мм, ${{l}_{{1,2,3}}}$ ∈ [200 мм, 500 мм] и диаметра штанги 100 мм введем дополнительные конструктивные ограничения ϑ₁; δ₁ ≥ 5°; 25.4° ≤ τ₁ ≤ 154.6°, где ϑ₁ – угол между звеньями A₁B₁ и B₁B₂; δ₁ – угол между звеньями A₁B₁ и B₁B₃, ограничивающие поворот во вращательном шарнире B₁; τ₁ – угол между штангой l₁ и основанием каркаса робота, исключающий соприкосновения между штангами плоского механизма и вертикальными стойками каркаса робота (рис. 12). Аналогично введем ограничения для двух других штанг на углы ϑ₂, δ₂, τ₂ и ϑ₃, δ₃, τ₃.

Результаты моделирования представлены на рис. 13. На рис. 13а показана трехмерная рабочая область робота с механизмами ОМ без учета конструктивных ограничений (темная область – объем, который исключается из рабочей области в процессе моделирования с учетом ограничений), на рис. 13б – с учетом конструктивных ограничений.

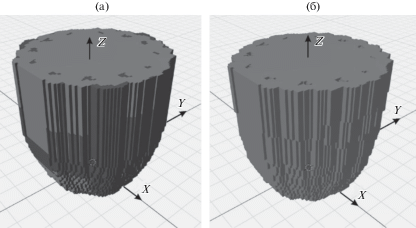
Объем рабочей области (рис. 13) при учете дополнительных конструктивных ограничений на углы поворота в шарнирах, а также возможных соприкосновений между звеньями плоского механизма и вертикальных стоек каркаса робота уменьшился с 0.469 м³ до 0.364 м³.

Далее исследуем влияние особых положений на вид и форму рабочей области робота с механизмами ОМ.

Рассмотрим подходы для определения особых положений механизмов параллельной структуры. Первый метод на основе анализа кинематических винтов, разработанный проф. В.А. Глазуновым, который позволяет выполнить анализ плоских и пространственных параллельных механизмов с помощью кинематических винтов [21]. При этом связи, налагаемые кинематическими цепями, представлены в виде силовых винтов. Если приводы зафиксированы, то данная система силовых винтов образует пространственную структуру, способную уравновесить силовое воздействие. Если же имеет место особое положение, то система силовых винтов вырождается, и возникает мгновенная неуправляемая подвижность вдоль одного кинематического винта. Второй метод, предложенный К. Гусленом [22], основан на анализе матрицы Якоби механизма, получаемой дифференцированием уравнений связи и описывающей переход от обобщенных скоростей в приводных кинематических парах к угловым или линейным скоростям выходного звена. С целью автоматизации расчетов при моделировании в статье использован второй метод.

Согласно классификации Гуслена [22] для трипода и плоского 3-RPR-механизма характерны сингулярности только второго типа, при которых равна нулю матрица Якоби.

Для модуля-трипода определитель матрицы Якоби имеет вид

где F_i соответствуют формулам длин штанг (8)–(10).

Ввиду громоздкости формул каждого из элементов определителя, приведем только один из них

где Ca = cos(θ); Ca = cos(θ), Cb = cos(ψ), Sa = sin(θ), Sb = sin(ψ).

Запишем условие возникновения особых положений

Для плоского 3-RPR-механизма определитель матрицы Якоби имеет вид

где F_i соответствуют формулам длин штанг (12)–(14)

Таким образом, формула (16) принимает вид

Особое положение возникает в том случае, если Якобиан (17) равен нулю, то есть det(J_A) = 0, что возможно при выполнении условий

Таким образом, чтобы платформа не проходила через особые положения согласно условию (18) углы ориентации платформы ${\varphi }$ должны быть либо только положительными, либо только отрицательными. Т.к. механизм является симметричным относительно оси Y, формы и размеры рабочей области будут идентичными при положительных и отрицательных φ. Для моделирования были выбраны положительные углы ${\varphi }$.

С учетом условий (15), (18), (19) синтезирован алгоритм рабочей области робота с механизмами ОМ с учетом особых положений отдельных модулей.

На рис. 14а показана трехмерная рабочая область робота с механизмами ОМ только с учетом конструктивных ограничений (темная область – объем, который исключается из рабочей области в процессе моделирования особых положений), на рис. 14б – с учетом конструктивных ограничений и особых положений.

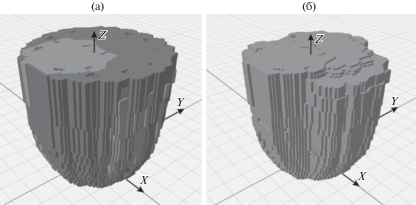
Объем рабочей области (рис. 14) при учете особых положений модулей уменьшился с 0.364 м³ до 0.205 м³ по сравнению с рабочей областью, представленной на рис. 14а.

Заключение. В статье рассмотрен робот с механизмами относительного манипулирования, который состоит из верхнего модуля-трипода с поступательными приводными кинематическими парами и нижнего модуля, выполненного на основе плоского 3-RРR-механизма с поступательными приводными кинематическими парами. Разработан численный метод определения рабочей области робота, основанный на концепции неравномерных покрытий, который позволяет учитывать конструктивные ограничения механизма, интерференцию звеньев и особые положения. В результате рабочая область реального механизма уменьшилась по сравнению с теоретической с 0.469 м³ до 0.205 м³. В связи с увеличением объема расчетов снизилась скорость работы программы. С целью увеличения быстродействия выполнения программы была применена многопоточность с использованием пакета OpenMP для вычислений, к которым применимо распараллеливание аналогичных операций, которые могут выполняться одновременно. Это позволило эффективно распределить вычислительную нагрузку в восьмиядерной системе с общей памятью и добиться существенного ускорения расчетов.