Проблемы машиностроения и надежности машин, 2020, № 6, стр. 48-60
О самосинхронизации колебаний вибрационной щековой дробилки при учете взаимодействия с обрабатываемой средой
А. Е. Шохин *
Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия
* E-mail: shohinsn@mail.ru
Поступила в редакцию 03.03.2020
Принята к публикации 29.07.2020
Аннотация
В статье рассмотрены колебания модели вибрационной щековой дробилки, возбуждаемые двумя самосинхронизирующимися дебалансными вибровозбудителями, при учете взаимодействия с обрабатываемой средой. Установлено, что области частот устойчивой противофазной синхронизации вращения вибровозбудителей, требуемой для нормальной работы дробилки, существенно зависят от зазора между щекой и элементом среды, причем уменьшение исходного зазора приводит к расширению области частот устойчивой противофазной синхронизации вибровозбудителей. При отсутствии исходного зазора и возникновении давления среды на щеки в зарезонансной области частот возможно появление области устойчивости синхронно-синфазного вращения вибровозбудителей. Показано, что при неизменной частоте возбуждения колебаний изменение исходного зазора между щеками и обрабатываемой средой может приводить к изменению типа синхронизации вращения вибровозбудителей и соответственно колебаний щек.
Одной из проблем создания вибрационных щековых дробилок (ВЩД) с самосинхронизирующимися дебалансными возбудителями колебаний является обеспечение требуемого синхронного режима колебаний щек и соответственно типа синхронизации вращения вибровозбудителей. Несмотря на значительные успехи в применении теории синхронизации динамических систем при разработке ВЩД, в практике их эксплуатации регулярно наблюдаются непрогнозируемые смены синхронного противофазного движения щек на синхронное синфазное, при котором эффективность дробления существенно снижается или дробление практически не происходит.
Анализу динамики ВЩД и методам их проектирования посвящено множество работ. Общим вопросам и теории самосинхронизации дебалансных вибровозбудителей в колебательных системах посвящены работы [1–3]. В работе [4] представлен подробный обзор конструктивных схем щековых дробилок, а так же основные методы анализа динамики и расчета конструктивных параметров дробилок с двумя качающимися щеками. Вопросы динамики ВЩД с нежестким закреплением вибровозбудителей на щеках без учета взаимодействия с обрабатываемой средой рассматривались в работе [5]. Отметим, что известные математические модели, применяемые для анализа динамики таких дробилок, включают ряд допущений о характере их движения и взаимодействии их элементов с обрабатываемой средой, которые с одной стороны существенно упрощают процесс анализа, а с другой – могут приводить к потере описания некоторых практически важных эффектов [1, 3, 6, 7]. Например, в [8–10] при анализе динамики дробилки с двумя подвижными щеками предполагается, что взаимодействие щек с обрабатываемой средой происходит одновременно с обеими щеками и учитывается в виде линейной вязкости. При этих допущениях не учитывается виброударный характер взаимодействия щек со средой, приводящий к необходимости рассмотрения существенно-нелинейной колебательной системы. Некоторые вопросы самосинхронизации колебаний ВЩД при учете обрабатываемой среды рассмотрены в работах [3, 11, 12]. В работе [12] проведен анализ взаимодействия обрабатываемой среды со щеками дробилки с прямолинейным движением щек в предположении о заданном законе их движения. В работе [13] описана многомассовая инерционная реологическая модель обрабатываемой среды, учитывающая ее деформации и перемещения в плоскости колебаний щек, а также ее взаимодействие со щеками как в направлении нормали их поверхности, так и по касательной. При расчете динамики щековой дробилки с использованием этой модели авторы рассматривают только симметричные условия контакта щек с обрабатываемой средой. Применение этой модели на практике затруднено необходимостью определения значительного количества параметров.
При практических расчетах часто ограничиваются рассмотрением колебаний вдали от резонансных частот, вблизи которых обычно расположены границы частотных диапазонов устойчивости требуемых синхронных режимов колебаний дробилки [4, 5, 10]. Резонансные частоты и указанные границы устойчивости определяются как конструктивными параметрами дробилки, так и свойствами обрабатываемого материала и характером его движения в рабочей зоне дробилки. При этом нелинейность сил взаимодействия рабочих органов дробилки с обрабатываемой средой может приводить к значительному изменению динамических свойств дробилки [6, 14]. Кроме того, задача обеспечения постоянства свойств обрабатываемого материала в рабочей камере дробилки оказывается трудно разрешимой. В связи с этим на практике оказывается затруднительным обеспечить возбуждение колебаний дробилки на достаточном удалении от границ устойчивости, что может приводить к смене режимов ее колебаний. Таким образом, вопросы учета взаимодействия рабочих органов с обрабатываемым материалом и его влияния на динамику дробилок приобретают особое значение при разработке ВЩД с самосинхронизирующимися дебалансными возбудителями колебаний.
В настоящей статье рассматривается модель ВЩД с двумя подвижными щеками, совершающими прямолинейные колебания, возбуждаемые самосинхронизирующимися дебалансными вибровозбудителями, установленными на щеках. С целью выявления возможного влияния свойств обрабатываемой среды на синхронизацию вращения вибровозбудителей и колебаний щек дробилки проводится анализ динамики ее модели с учетом прерывистого взаимодействия щек с обрабатываемой средой.
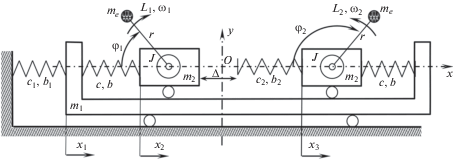
Математическая модель и методы моделирования. Расчетная схема модели дробилки с поступательными колебаниями щек представлена на рис. 1. Модель состоит из жесткой рамы, моделируемой твердым телом массой m1, и двух подвижных щек, моделируемых твердыми телами с одинаковой массой m2. Рама закреплена относительно неподвижного основания с помощью линейной пружины с коэффициентами жесткости и вязкости соответственно c1 и b1. Левая и правая щеки упруго закреплены относительно рамы с помощью одинаковых линейных пружин с коэффициентами жесткости и вязкости соответственно c и b. Перемещения каждого из тел описываются перемещениями x1, x2, x3 их центров масс вдоль горизонтальной оси Ox относительно положений равновесия. Взаимодействие щек с обрабатываемой средой моделируется линейной пружиной с коэффициентами жесткости и вязкости соответственно c2 и b2, закрепленной на правой щеке и установленной с зазором Δ относительно левой щеки. При этом величина Δ характеризует степень наполненности рабочей камеры дробилки обрабатываемой средой. Уменьшение величины Δ соответствует увеличению наполненности объема рабочей камеры дробилки. Значения Δ < 0 соответствуют возникновению давления среды на щеки. Таким образом, взаимодействие щек с обрабатываемой средой описывается кусочно-линейной функцией вида
(1)
${\Phi }* = \left\{ {\begin{array}{*{20}{l}} {0,\quad {\text{при}}\quad {{x}_{2}} - {{x}_{3}} - \Delta \leqslant 0,} \\ {{{c}_{2}}\left( {{{x}_{2}} - {{x}_{3}} - \Delta } \right) + {{b}_{2}}\left( {{{{\dot {x}}}_{2}} - {{{\dot {x}}}_{3}}} \right),\quad {\text{при}}\quad {{x}_{2}} - {{x}_{3}} - \Delta > 0.} \end{array}} \right.$Колебания системы возбуждаются с помощью двух одинаковых дебалансных вибровозбудителей с массой дисбаланса me и эксцентриситетом r, жестко закрепленных на щеках. Вращение каждого из дебалансов осуществляется асинхронным электродвигателем, с приведенным к валу моментом инерции J0. Крутящий момент каждого двигателя описывается его статической характеристикой [6], который с учетом момента трения в опорных подшипниках вала дебаланса описывается функцией Li (i = 1, 2 – номер дебаланса). Положения дисбалансов описываются углами поворота φi, отсчитываемыми от отрицательного направления оси Ox.
Уравнения движения системы имеют вид
(2)
$\left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{l}} {{\mathbf{M\ddot {X}}} + {\mathbf{CX}} = - {\mathbf{B\dot {X}}} + {\mathbf{\Phi }} + {\mathbf{P}},} \\ {J{{{\ddot {\varphi }}}_{1}} = {{L}_{1}}\left( {{{{\dot {\varphi }}}_{1}}} \right) + {{m}_{e}}r{{{\ddot {x}}}_{2}}\sin {{\varphi }_{1}},} \\ {J{{{\ddot {\varphi }}}_{2}} = {{L}_{2}}\left( {{{{\dot {\varphi }}}_{2}}} \right) + {{m}_{e}}r{{{\ddot {x}}}_{3}}\sin {{\varphi }_{2}},} \end{array}} \end{array}} \right.$Вводя замену переменных ${{x}_{j}} = \sum\nolimits_{i = 1}^3 {{{u}_{{ij}}}{{q}_{i}}} $, ( j = 1, 2, 3), где uij – элементы матрицы ${\mathbf{U}} = \left[ {\begin{array}{*{20}{c}} {{{u}_{{11}}}}&0&{{{u}_{{31}}}} \\ 1&{ - 1}&1 \\ 1&1&1 \end{array}} \right]$, составленной из собственных векторов для порождающей системы первых трех уравнений (2), получим систему уравнений движения относительно новых (главных) координат qi
(3)
$\left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{l}} {{{{\ddot {q}}}_{1}} + p_{1}^{2}{{q}_{1}} = [ - b_{{11}}^{*}{{{\dot {q}}}_{1}} - b_{{13}}^{*}{{{\dot {q}}}_{3}} + {{P}_{2}} + {{P}_{3}}]{\text{/}}m_{{11}}^{*},} \\ {{{{\ddot {q}}}_{2}} + p_{2}^{2}{{q}_{2}} = [ - b_{{22}}^{*}{{{\dot {q}}}_{2}} + 2{\Phi }{\kern 1pt} *{\kern 1pt} ({{q}_{2}},{{{\dot {q}}}_{2}}) - {{P}_{2}} + {{P}_{3}}]{\text{/}}m_{{22}}^{*},} \\ {{{{\ddot {q}}}_{3}} + p_{3}^{2}{{q}_{3}} = [ - b_{{31}}^{*}{{{\dot {q}}}_{1}} - b_{{33}}^{*}{{{\dot {q}}}_{3}} + {{P}_{2}} + {{P}_{3}}]{\text{/}}m_{{33}}^{*},} \\ {{{{\ddot {\varphi }}}_{1}} = [{{L}_{1}}({{{{\dot {\varphi }}}}_{1}}) + {{m}_{e}}r({{{\ddot {q}}}_{1}} - {{{\ddot {q}}}_{2}} + {{{\ddot {q}}}_{3}}){\text{sin}}{{{\varphi }}_{1}}]{\text{/}}J,} \\ {{{{\ddot {\varphi }}}_{2}} = \left[ {{{L}_{2}}({{{{\dot {\varphi }}}}_{2}}) + {{m}_{e}}r({{{\ddot {q}}}_{1}} + {{{\ddot {q}}}_{2}} + {{{\ddot {q}}}_{3}}){\text{sin}}{{{\varphi }}_{2}}} \right]{\text{/}}J,} \end{array}} \end{array}} \right.$Выбирая масштаб времени ${{T}_{*}} = {\text{1/}}{{p}_{2}}$ и масштаб перемещений ${{X}_{*}} = {{m}_{e}}r{\text{/}}m_{{22}}^{*}$, и вводя безразмерное время $t = {\tau /}{{T}_{*}}$ и координаты ${{y}_{j}} = {{q}_{j}}{\text{/}}{{X}_{*}}$, приведем систему (3) к безразмерному виду
(4)
$\left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{l}} {{{{\ddot {y}}}_{1}} + 2{\lambda }{{{\mu }}_{1}}\left( {{{{\beta }}_{1}}{{{\dot {y}}}_{1}} + {{{\beta }}_{4}}{{{\dot {y}}}_{3}}} \right) + n_{1}^{2}{{y}_{1}} = {{{\mu }}_{1}}\left( {\mathop \sum \limits_{i = 1}^2 ({{{\ddot {\varphi }}}_{i}}\sin {{\varphi }_{i}} + \dot {\varphi }_{i}^{2}\cos {{\varphi }_{i}})} \right),} \\ {{{{\ddot {y}}}_{2}} + 2{\lambda }{{{\dot {y}}}_{2}} + {{y}_{2}} - 2{\Phi **}\left( {{{y}_{2}},{{{\dot {y}}}_{2}}} \right) = \left( {\mathop \sum \limits_{i = 1}^2 {{{\left( { - 1} \right)}}^{i}}({{{\ddot {\varphi }}}_{i}}\sin {{\varphi }_{i}} + \dot {\varphi }_{i}^{2}\cos {{\varphi }_{i}})} \right),} \\ {{{{\ddot {y}}}_{3}} + 2{\lambda }{{{\mu }}_{2}}\left( {{{{\beta }}_{4}}{{{\dot {y}}}_{1}} + {{{\beta }}_{3}}{{{\dot {y}}}_{3}}} \right) + n_{3}^{2}{{y}_{3}} = {{{\mu }}_{2}}\left( {\mathop \sum \limits_{i = 1}^2 ({{{\ddot {\varphi }}}_{i}}\sin {{\varphi }_{i}} + \dot {\varphi }_{i}^{2}\cos {{\varphi }_{i}})} \right),} \\ {{{{\ddot {\varphi }}}_{1}} = {{N}_{1}}\left( {{{{\dot {\varphi }}}_{1}}} \right) + {{J}_{*}}\left( {{{{\ddot {y}}}_{1}} - {{{\ddot {y}}}_{2}} + {{{\ddot {y}}}_{3}}} \right)\sin {{\varphi }_{1}},} \\ {{{{\ddot {\varphi }}}_{2}} = {{N}_{2}}\left( {{{{\dot {\varphi }}}_{2}}} \right) + {{J}_{*}}\left( {{{{\ddot {y}}}_{1}} + {{{\ddot {y}}}_{2}} + {{{\ddot {y}}}_{3}}} \right)\sin {{\varphi }_{2}},} \end{array}} \end{array}} \right.$Система (4) полностью эквивалентна системе (2) однако более удобна для анализа, т.к. существенно-нелинейная функция Φ** содержится только в одном уравнении.
В рамках рассматриваемой постановки задачи будем искать решения системы соответствующие установившимся одночастотным близким к 2π периодическим по ωt режимам колебаний дробилки при синхронном практически равномерном вращении вибровозбудителей, поскольку именно такие режимы представляют наибольший практический интерес. Решение поставленной задачи получим методами прямого разделения движения и гармонической линеаризации [6, 15, 16]. Учитывая несимметричную характеристику нелинейности во втором уравнении системы (4), приближенные решения, описывающие колебания тел, будем искать в форме
Для дальнейшего построения решения выполним гармоническую линеаризацию Φ**, ограничиваясь учетом в решении ${{\tilde {y}}_{j}}$ только первой гармоники. Учет более высоких гармоник не вызывает принципиальных затруднений, однако как отмечено в [15] основная качественная информация о свойствах сильно нелинейных систем отражается первой гармоникой колебаний. С учетом предполагаемого характера решений линеаризованное выражение для Φ** примет вид
Линеаризуем так же моментные характеристики двигателей ${{N}_{i}}\left( {{{{{\dot {\varphi }}}}_{i}}} \right)$ вблизи парциальной частоты вращения вибровозбудителей ${{\dot {\varphi }}_{i}} = {{\sigma }_{i}}{{\omega }_{{pi}}}$ (т.е. частоты вращения при установке вибровозбудителя на неподвижном основании), полагая ее близкой к рабочей частоте
Подставляя полученные выражения в (4), и применяя метод прямого разделения движений, получим систему уравнений в виде
(5)
$\left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{l}} {{{{\ddot {\tilde {y}}}}_{1}} + 2\lambda {{\mu }_{1}}({{\beta }_{1}}{{{\dot {\tilde {y}}}}_{1}} + {{\beta }_{4}}{{{\dot {\tilde {y}}}}_{3}}) + n_{1}^{2}{{{\tilde {y}}}_{1}} = {{\mu }_{1}}\left( {\mathop \sum \limits_{i = 1}^2 ({{{\ddot {\varphi }}}_{i}}\sin {{\varphi }_{i}} + \dot {\varphi }_{i}^{2}\cos {{\varphi }_{i}})} \right),} \\ {{{{\ddot {\tilde {y}}}}_{2}} + (2\lambda - 2{{\beta }_{*}}){{{\dot {\tilde {y}}}}_{2}} + (1 - 2k){{{\tilde {y}}}_{2}} = \left( {\mathop \sum \limits_{i = 1}^2 {{{\left( { - 1} \right)}}^{i}}({{{\ddot {\varphi }}}_{i}}\sin {{\varphi }_{i}} + \dot {\varphi }_{i}^{2}\cos {{\varphi }_{i}})} \right),} \\ {{{{\ddot {\tilde {y}}}}_{3}} + 2\lambda {{\mu }_{2}}({{\beta }_{4}}{{{\dot {\tilde {y}}}}_{1}} + {{\beta }_{3}}{{{\dot {\tilde {y}}}}_{3}}) + n_{3}^{2}{{{\tilde {y}}}_{3}} = {{\mu }_{2}}\left( {\mathop \sum \limits_{i = 1}^2 ({{{\ddot {\varphi }}}_{i}}\sin {{\varphi }_{i}} + \dot {\varphi }_{i}^{2}\cos {{\varphi }_{i}})} \right),} \\ {{{{\dot {\omega }}}_{{{v}1}}} = - {{h}_{1}}{{\omega }_{{{v}1}}} + {{\sigma }_{1}}V_{1}^{*},} \\ {{{{\dot {\omega }}}_{{{v}2}}} = - {{h}_{2}}{{\omega }_{{{v}2}}} + {{\sigma }_{2}}V_{2}^{*},} \\ {{{{\dot {\omega }}}_{1}} = - {{h}_{1}}({{\omega }_{1}} - {{\omega }_{{p1}}}) + {{\sigma }_{1}}[{{N}_{{01}}}({{\sigma }_{1}}{{\omega }_{{p1}}}) + {{V}_{1}}],} \\ {{{{\dot {\omega }}}_{2}} = - {{h}_{2}}({{\omega }_{2}} - {{\omega }_{{p2}}}) + {{\sigma }_{2}}[{{N}_{{02}}}({{\sigma }_{2}}{{\omega }_{{p2}}}) + {{V}_{2}}],} \end{array}} \end{array}} \right.$Полученная система уравнений включает уравнения, описывающие быстрые движения – первые пять уравнений (5), и уравнения для медленных движений – последние два уравнения (5). В разыскиваемых установившихся синхронных режимах движения системы величины $V_{1}^{*}$ и $V_{2}^{*}$ можно считать малыми, и их можно представить в виде $V_{i}^{*} = {\varepsilon }V_{1}^{{{\text{**}}}}$, где ${\varepsilon }$ – малый параметр. Разыскивая решения (5) в виде рядов по степеням ${\varepsilon }$, после подстановки их в (5) и выполнения преобразований, получим систему уравнений для определения решений в первом приближении в виде
(6)
$\left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{l}} {{{{\ddot {\tilde {y}}}}_{1}} + 2\lambda {{\mu }_{1}}({{\beta }_{1}}{{{\dot {\tilde {y}}}}_{1}} + {{\beta }_{4}}{{{\dot {\tilde {y}}}}_{3}}) + n_{1}^{2}{{{\tilde {y}}}_{1}} = {{\mu }_{1}}\left( {\mathop \sum \limits_{i = 1}^2 \,\dot {\varphi }_{i}^{2}\cos {{\varphi }_{i}}} \right),} \\ {{{{\ddot {\tilde {y}}}}_{2}} + (2\lambda - 2{{\beta }_{*}}){{{\dot {\tilde {y}}}}_{2}} + \left( {1 - 2k} \right){{{\tilde {y}}}_{2}} = \left( {\mathop \sum \limits_{i = 1}^2 {{{\left( { - 1} \right)}}^{i}}\dot {\varphi }_{i}^{2}\cos {{\varphi }_{i}}} \right),} \\ {{{{\ddot {\tilde {y}}}}_{3}} + 2\lambda {{\mu }_{2}}({{\beta }_{4}}{{{\dot {\tilde {y}}}}_{1}} + {{\beta }_{3}}{{{\dot {\tilde {y}}}}_{3}}) + n_{3}^{2}{{{\tilde {y}}}_{3}} = {{\mu }_{2}}\left( {\mathop \sum \limits_{i = 1}^2 \,\dot {\varphi }_{i}^{2}\cos {{\varphi }_{i}}} \right),} \\ {{{{\dot {\omega }}}_{{{v}1}}} = - {{h}_{1}}{{\omega }_{{{v}1}}},} \\ {{{{\dot {\omega }}}_{{{v}2}}} = - {{h}_{2}}{{\omega }_{{{v}2}}},} \\ {{{{\dot {\omega }}}_{1}} = - {{h}_{1}}({{\omega }_{1}} - {{\omega }_{{p1}}}) + {{\sigma }_{1}}[{{N}_{{01}}}({{\sigma }_{1}}{{\omega }_{{p1}}}) + {{V}_{1}}],} \\ {{{{\dot {\omega }}}_{2}} = - {{h}_{2}}({{\omega }_{2}} - {{\omega }_{{p2}}}) + {{\sigma }_{2}}[{{N}_{{02}}}({{\sigma }_{2}}{{\omega }_{{p2}}}) + {{V}_{2}}].} \end{array}} \end{array}} \right.$Стационарным решениям (6) соответствуют значения частот ${{{\omega }}_{{01}}}$ = ${{{\omega }}_{{02}}}$ = ${{{\omega }}_{{{v}1}}}$ = ${{{\omega }}_{{{v}2}}}$ = 0, и фаз ${{\alpha }_{i}} = \operatorname{const} $. При этом вращение вибровозбудителей определяется выражением ${{\varphi }_{i}} = {{\sigma }_{i}}(\omega t + {{\alpha }_{i}})$, ${{\dot {\varphi }}_{i}} = {{\sigma }_{i}}\omega $ и соответствует равномерному вращению с постоянной частотой ω, которая определяется из дальнейшего решения (6). Рассматривая частоту ω в качестве параметра и подставляя выражения для ${{{\varphi }}_{i}}$ в первые три уравнения (6) определяем решения ${{\tilde {y}}_{j}}$
(7)
${{\tilde {y}}_{2}} = {{B}_{{21}}}\,\mathop \sum \limits_{i = 1}^2 {{\left( { - 1} \right)}^{i}}\cos {{\varphi }_{i}} + {{D}_{{21}}}\,\mathop \sum \limits_{i = 1}^2 {{\left( { - 1} \right)}^{i}}\sin {{\varphi }_{i}},$где ${{B}_{{j1}}} = \operatorname{Re} (A_{{j1}}^{*})$; ${{D}_{{j1}}} = \operatorname{Im} (A_{{j1}}^{*})$; $A_{{11}}^{*} = {{\omega }^{2}}\frac{{{{\mu }_{1}}{{L}_{{33}}} - {{\mu }_{2}}{{L}_{{13}}}}}{{{{L}_{{11}}}{{L}_{{33}}} - {{L}_{{13}}}{{L}_{{31}}}}}$; $A_{{21}}^{*}$ = ${{\omega }^{2}}\frac{1}{{{{L}_{{22}}}}}$; $A_{{31}}^{*}$ = = ${{\omega }^{2}}\frac{{{{\mu }_{2}}{{L}_{{11}}} - {{\mu }_{1}}{{L}_{{31}}}}}{{{{L}_{{11}}}{{L}_{{33}}} - {{L}_{{13}}}{{L}_{{31}}}}}$; ${{L}_{{11}}} = n_{1}^{2} - {{\omega }^{2}}$ + $2\lambda {{\mu }_{1}}{{\beta }_{1}}\omega {\mathbf{i}}$; ${{L}_{{13}}} = 2\lambda {{\mu }_{1}}{{\beta }_{4}}\omega {\mathbf{i}}$; ${{L}_{{22}}} = (1 - 2k) - {{\omega }^{2}}$ + $(2\lambda $ – – $2{{\beta }_{*}})\omega {\mathbf{i}}$; ${{L}_{{31}}} = 2\lambda {{\mu }_{2}}{{\beta }_{4}}\omega {\mathbf{i}}$; ${{L}_{{33}}} = n_{3}^{2} - {{\omega }^{2}}$ + $2\lambda {{\mu }_{2}}{{\beta }_{3}}\omega {\mathbf{i}}$; ${\mathbf{i}} = \sqrt { - 1} $.
Далее для определенности будем считать, что приводные электродвигатели вибровозбудителей обладают одинаковыми моментными характеристиками (данное условие обычно выполняется на практике за счет соответствующего подбора электродвигателей). Следовательно, ${{h}_{1}} = {{h}_{2}} = h$, ${{{\omega }}_{{p1}}} = {{{\omega }}_{{p2}}} = {{{\omega }}_{p}}$, ${{\sigma }_{1}}{{N}_{{01}}}({{\sigma }_{1}}{{\omega }_{{p1}}})$ = ${{\sigma }_{2}}{{N}_{{02}}}({{\sigma }_{2}}{{\omega }_{{p2}}})$ = = ${{N}_{0}}({{\omega }_{p}})$, где в соответствии с выбранными направлениями вращений (рис. 1) σ1 = 1, σ2 = 1. Тогда, подставляя найденные решения для быстрых движений (7) в последние два уравнения (6) и выполняя усреднение по ωt, получим систему из двух уравнений для определения частоты ω и взаимной фазы вращения вибровозбудителей α = α2 – α1
(8)
$\left\{ {\begin{array}{*{20}{l}} { - h\left( {\omega - {{\omega }_{p}}} \right) + {{N}_{0}}\left( {{{\omega }_{p}}} \right) - \frac{1}{2}{{J}_{*}}{{\omega }^{2}}\left( {{{H}_{1}}\sin \left( \alpha \right) + {{Q}_{2}} + {{Q}_{1}}\cos \left( \alpha \right)} \right) = 0,} \\ { - h\left( {\omega - {{\omega }_{p}}} \right) + {{N}_{0}}\left( {{{\omega }_{p}}} \right) - \frac{1}{2}{{J}_{*}}{{\omega }^{2}}\left( { - {{H}_{1}}\sin \left( \alpha \right) + {{Q}_{2}} + {{Q}_{1}}\cos \left( \alpha \right)} \right) = 0,} \end{array}} \right.$Вычитая из первого уравнения системы (8) второе уравнение получим уравнение
которое имеет два различных решения: α = 0 соответствующее синхронному синфазному вращению вибровозбудителей, и α = π – соответствующее их синхронному противофазному вращению.Складывая оба уравнения системы (8) получим уравнение
Анализ устойчивости найденных решений проводится известными методами теории устойчивости [6, 16, 17] на основе анализа корней характеристического уравнения для системы уравнений в вариациях. Для этого в первую очередь определяются асимптотически устойчивые решения для системы уравнений, описывающих быстрые движения. Далее для выбранных устойчивых решений быстрых движений выполняется проверка на устойчивость по уравнениям в вариациях для медленных движений, которые имеют вид
Уравнения в вариациях для быстрых движений в настоящей статье не приводятся ввиду громоздкости их выражений вследствие высокого порядка системы. Их получение не вызывает принципиальных затруднений, а анализ характеристических показателей выполняется численно.
Анализ устойчивости решений существенно упрощается при рассмотрении колебаний вдали от резонанса [1, 14]. В этом случае устойчивость решений определяется корнем χ уравнения
Решения устойчивы при χ < 0, и, следовательно, критерий устойчивости можно записать в виде $ - {{J}_{*}}{{\omega }^{2}}{{H}_{1}}\cos \left( \alpha \right) < 0$.
Результаты моделирования. Для выявления влияния взаимодействия щек с обрабатываемой средой на синхронные режимы вращения вибровозбудителей и колебаний щек рассматривались колебания модели дробилки при различной степени наполненности ее рабочей камеры, характеризуемой величиной исходного зазора Δ*. Расчеты проводились при варьировании значений исходного зазора в диапазоне Δ* = [–10, 20]. В результате расчетов были получены амплитудно-частотные характеристики системы (АЧХ) и определены области частот с устойчивыми синхронными синфазным и противофазным вращениями вибровозбудителей и колебаниями щек (в дальнейшем говоря о синхронном противофазном или синфазном вращении вибровозбудителей будем подразумевать и соответствующие синхронные колебания щек). Полученные результаты сравнивались с аналогичными характеристиками для модели дробилки, в которой не учитывается прерывистое взаимодействие щек с обрабатываемой средой (подобные модели обычно применяются при практических расчетах ВЩД). Последняя модель формально была получена из исходной при выборе величины зазора Δ* заведомо в несколько раз большей, чем максимальная величина амплитуды колебаний A21 в исследуемом диапазоне частот ω. Расчеты проводились при следующих значениях параметров системы: ${{n}_{1}} = 0.166$; ${{n}_{2}} = 6$; ${{n}_{3}} = 1.515$; ${{{\mu }}_{1}} = 1$; ${{{\mu }}_{2}} = 1$; ${{{\beta }}_{1}} = 0.271$; ${{{\beta }}_{2}} = 10$; ${{{\beta }}_{3}} = 2.623$; ${{{\beta }}_{4}} = - 0.281$; ${\lambda } = 0.03$; $h = 100$; ${{J}_{*}} = 0.05$.
На рис. 2 представлены АЧХ для каждой из координат ${{\tilde {y}}_{j}}$ системы для модели дробилки, в которой не учитывается прерывистое взаимодействие щек с обрабатываемой средой. Номера линий на графиках соответствуют номерам координат. Представленные АЧХ координат ${{\tilde {y}}_{1}}$ и ${{\tilde {y}}_{3}}$ соответствуют случаю α = 0 (при котором, в соответствии со структурой уравнений (7), ${{\tilde {y}}_{2}} = 0$ во всей частотной области), а АЧХ координаты ${{\tilde {y}}_{2}}$ соответствует случаю α = π (при котором во всей частотной области ${{\tilde {y}}_{1}} = {{\tilde {y}}_{3}} = 0$). Жирными точками на кривых 1 и 3 отмечены участки характеристик, соответствующие устойчивым режимам с синхронным синфазным вращением вибровозбудителей (α = 0), а на кривой 2 – соответствующие устойчивым режимам с синхронным противофазным вращением вибровозбудителей (α = π). Видно, что при возбуждении колебаний в областях частот между первой и второй резонансными частотами системы и за третьей резонансной частотой, т.е. при ${\omega }$ ∈ $(p_{1}^{*},1)$ ∪ $(p_{3}^{*},\infty )$, $(p_{1}^{*} = {{n}_{1}}$, $p_{3}^{*} = {{n}_{3}})$, реализуются синхронные режимы с устойчивым противофазным вращением вибровозбудителей. В остальных областях частот устойчивыми являются режимы с синхронным синфазным вращением вибровозбудителей.
Рис. 2.
АЧХ модели дробилки не учитывающей прерывистое взаимодействие между щеками и обрабатываемой средой: 1 – для координаты ${{\tilde {y}}_{1}}$ при α = 0; 2 – для координаты ${{\tilde {y}}_{2}}$ при α = π; 3 – для координаты ${{\tilde {y}}_{3}}$ при α = 0.
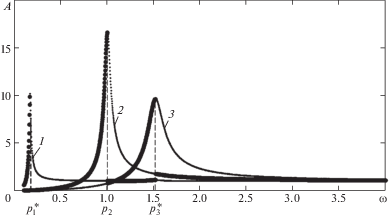
На рис. 3–5 представлены АЧХ для каждой из координат ${{\tilde {y}}_{j}}$ системы для модели дробилки учитывающей прерывистое взаимодействие щек с обрабатываемой средой, полученные при значениях зазора ${\Delta *}$ = {20; 5; 0; –5; –10} соответственно. Принятые на этих рисунках обозначения аналогичны обозначениям на рис. 2. Видно, что АЧХ первой и третьей координат системы, а, следовательно, первая и третья резонансные частоты, в первом приближении не зависят от Δ* (как и следовало ожидать исходя из вида уравнений (7)). АЧХ координаты ${{\tilde {y}}_{2}}$ и области частот устойчивой противофазной синхронизации вращения вибровозбудителей оказываются существенно зависящими от Δ*.
Рис. 3.
АЧХ модели дробилки: (а) – при Δ* = 20, (б) – при Δ* = 5; 1 – для координаты ${{\tilde {y}}_{1}}$ при α = 0; 2 – для координаты ${{\tilde {y}}_{2}}$ при α = π; 3 – для координаты ${{\tilde {y}}_{3}}$ при α = 0.
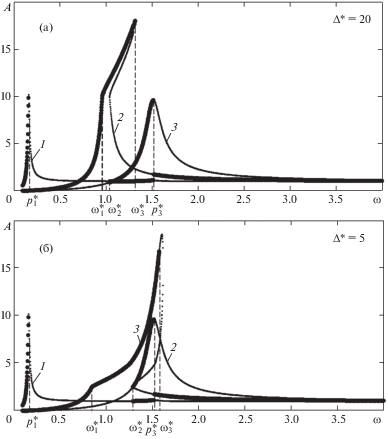
Рис. 4.
АЧХ модели дробилки при Δ* = 0: 1 – для координаты ${{\tilde {y}}_{1}}$ при α = 0; 2 – для координаты ${{\tilde {y}}_{2}}$ при α = π; 3 – для координаты ${{\tilde {y}}_{3}}$ при α = 0.
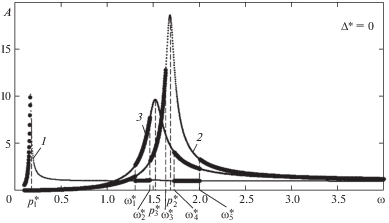
Рис. 5.
АЧХ модели дробилки: (а) – при Δ* = – 5; (б) – при Δ* = –10; 1 – для координаты ${{\tilde {y}}_{1}}$ при α = 0; 2 – для координаты ${{\tilde {y}}_{2}}$ при α = π; 3 – для координаты ${{\tilde {y}}_{3}}$ при α = 0.
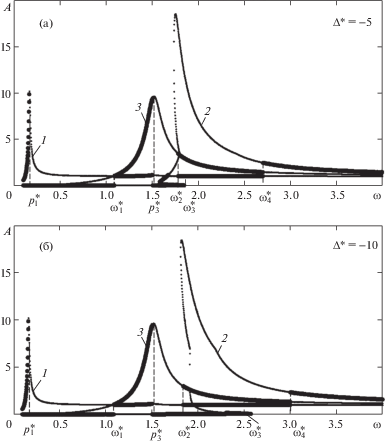
При Δ* > 0 (рис. 3) АЧХ модели соответствует системе с жесткой характеристикой нелинейности. При этом наблюдается расширение области частот устойчивой противофазной синхронизации вращения вибровозбудителей за счет увеличения второй резонансной частоты. Отметим, что рабочим режимам дробилки соответствует лишь область частот ${\omega } \in ({\omega }_{1}^{*},{\omega }_{3}^{*})$, в которой происходит взаимодействие щек с обрабатываемой средой. С уменьшением Δ* область частот устойчивой противофазной синхронизации расширяется. В области частот $\omega \in (\omega _{1}^{*},\omega _{3}^{*})$ ∩ $(\omega _{2}^{*},p_{3}^{*})$ могут реализовываться как устойчивые синхронно-синфазные режимы колебаний так и устойчивые синхронно-противофазные режимы колебаний.
При Δ* = 0 (рис. 4) система становится изохронной с увеличенной (по отношению к системе, не учитывающей прерывистое взаимодействие щек со средой) приблизительно в $\sqrt 3 $ раз второй резонансной частотой. В этом случае колебания системы происходят при прерывистом взаимодействии щек со средой при любой ненулевой амплитуде колебаний координаты ${{\tilde {y}}_{2}}$. При этом область частот устойчивой противофазной синхронизации вращения вибровозбудителей состоит из трех участков ${\omega } \in (p_{1}^{*},{\omega }_{1}^{*})$ ∪ $({\omega }_{2}^{*},{\omega }_{3}^{*})$ ∪ $({\omega }_{5}^{*},\infty )$. Важно отметить, что в этом случае в области частот ${\omega } \in (p_{3}^{*},\infty )$ появляется область частот ${\omega } \in ({\omega }_{4}^{*},{\omega }_{5}^{*})$ с устойчивыми синхронно-синфазными режимами вращения вибровозбудителей, при которых не возбуждаются встречные колебания щек, необходимые для нормальной работы дробилки.
При Δ* < 0 (рис. 5) АЧХ модели соответствует системе с мягкой характеристикой нелинейности.
Область частот устойчивой противофазной синхронизации вибровозбудителей состоит из трех диапазонов ${\omega } \in (p_{1}^{*},{\omega }_{1}^{*})$ ∪ $(p_{3}^{*},{\omega }_{3}^{*})$ ∪ $({\omega }_{4}^{*},\infty )$. При этом в диапазоне частот ${\omega } \in (p_{1}^{*},{\omega }_{1}^{*})$ ∪ $(p_{3}^{*},{\omega }_{3}^{*})$, возбуждаемые противофазные колебания щек происходят без отрыва от обрабатываемой среды, что является малоэффективным для ее дробления. При ${\omega } > {\omega }_{4}^{*}$ возбуждаемые противофазные колебания щек соответствуют требуемому виброударному режиму их взаимодействия со средой. В области частот ${\omega } \in (p_{3}^{*},\infty )$ появляется область частот ${\omega } \in ({\omega }_{2}^{*},{\omega }_{4}^{*})$ с устойчивыми синхронно-синфазными режимами вращения вибровозбудителей. При уменьшении Δ* (т.е. при увеличении давления среды на щеки) наблюдается увеличение граничных частот ${\omega }_{2}^{*}$ и ${\omega }_{4}^{*}$, что означает увеличение нижней граничной частоты области рабочих частот дробилки.
Заключение. Представленная модель ВЩД в виде трехмассовой колебательной системы с самосинхронизирующимися дебалансными вибровозбудителями и нелинейным упруго-вязким элементом между щеками позволяет учесть прерывистый характер взаимодействия щек с обрабатываемым материалом, и проанализировать его влияние на синхронные режимы колебаний дробилки. В результате выполненного анализа динамики модели установлено, что области частот устойчивой противофазной синхронизации вращения вибровозбудителей, требуемой для нормальной работы дробилки, существенно зависят от зазора Δ* между щекой и элементом среды. Первая и третья резонансные частоты системы, оказались не зависящими от величины Δ*. Наиболее чувствительной к величине Δ* оказалась вторая резонансная частота. При значениях Δ* > 0, уменьшение Δ* (т.е. увеличение наполненности объема рабочей камеры дробилки) приводит к расширению области частот устойчивой противофазной синхронизации вибровозбудителей за счет увеличения второй резонансной частоты колебаний щек. При отсутствии исходного зазора и возникновении давления среды на щеки, в зарезонансной области частот (за третьим резонансом) возможно появление области частот устойчивой синфазной синхронизации вращения вибровозбудителей, которая при наличии зазора обычно является областью частот устойчивости синхронного противофазного вращения вибровозбудителей. Таким образом, при неизменной частоте возбуждения колебаний изменение исходного зазора между щеками и обрабатываемой средой может приводить к изменению типа синхронизации вращения вибровозбудителей и соответственно колебаний щек. Представленные результаты показывают, что при разработке ВЩД с самосинхронизирующимися вибровозбудителями следует применять модели, учитывающие упруго-диссипативные свойства обрабатываемой среды и прерывистый характер ее взаимодействия со щеками.
Список литературы
Блехман И.И. Синхронизация динамических систем. М.: Наука. 1971. 896 с.
Nijmeijer H., Rodriguez-Angeles A. Synchronization of mechanical systems. Singapore: World Scientific Publishing. 2003. 220 c.
Nagaev R. Dynamics of synchronizing systems. Berlin: Springer-Verlag. 2003. 326 c.
Вайсберг Л.А., Зарогатский Л.П., Туркин В.Я. Вибрационные дробилки. Основы расчета, проектирования и технологического применения. Санкт-Петербург: изд. ВСЕГЕИ. 2004. 305 с.
Нагаев Р.Ф., Туркин В.Я., Шишкин Е.В. Динамика вибрационной щековой дробилки с нежестким креплением вибровозбудителей // Обогащение руд. 2002. № 3. С. 140.
Blekhman I.I. Vibrational Mechanics. Nonlinear Dynamic Effects, General Approach, Applications. Singapore: World Scientific. 2000. 509 c.
Gouskov A.M., Panovko G.Ya. On parametric oscillations of pendular and rotor systems // Journal of Vibroengineering. 2008. V. 10. Iss. 3. C. 277.
Тягушев С.Ю., Туркин В.Я., Шонин О.Б. Стабилизация синхронно-противофазного режима вибрационной щековой дробилки средствами автоматизированного электропривода // Обогащение руд. 2011. № 2. С. 38.
Архипов М.Н., Ветюков М.М., Нагаев Р.Ф., Утимишев М.М. Динамика вибрационной щековой дробилки при учете влияния разрушаемого материала // Проблемы машиностроения и надежности машин. 2006. № 1. С. 21.
Шишкин Е.В., Сафронов А.Н. Динамика вибрационной щековой дробилки с учетом влияния технологической нагрузки // Обогащение руд. 2016. № 6. С. 39.
Нагаев Р.Ф., Карагулов Р.Р. Динамика вибрационной машины с учетом влияния обрабатываемого материала // Проблемы машиностроения и надежности машин. 2001. № 1. С. 48.
Нагаев Р.Ф., Утимишев М.М. О движении материала в рабочей полости вибрационной щековой дробилки // Проблемы машиностроения и надежности машин. 2002. № 1. С. 85.
Гончаревич И.Ф., Фролов К.В. Теория вибрационной техники и технологии. М.: Наука. 1981. 319 с.
Astashev V., Babitsky V., Kolovsky M. Dynamics and Control of Machines. Berlin: Springer. 2000. 233 c.
Babitsky V.I., Krupenin V.L. Vibration of Strongly Nonlinear Discontinuous Systems. Berlin, Heidelberg, New York: Springer-Verlag. 2001. 404 c.
Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. М.: Наука. 1975. 768 с.
Малкин И.Г. Теория устойчивости движения, М.: Наука, 1966. 531 с.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин